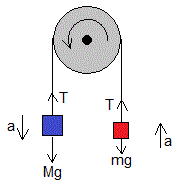
Dibujamos las fuerzas (peso y la tensión T de la cuerda) sobre cada uno de los dos cuerpos y aplicamos la segunda ley de Newton. La aceleración a de los cuerpos es la misma al estar unidos por una cuerda inextensible

${\displaystyle \begin{array}{l}\{\begin{array}{l}Mg-T=Ma\\ T-mg=ma\end{array}\\ a=\frac{M-m}{M+m}g\end{array}}$

Sin rozamiento

Un cuerpo de masa m puede deslizar por un plano horizontal, está unido a otro cuerpo que cuelga de masa M por una cuerda inextensible y de masa despreciable. La cuerda pasa por una polea ideal de radio muy pequeño y momento de inercia despreciable

En este apartado, estudiamos el movimiento del bloque de masa m en ausencia de rozamiento.

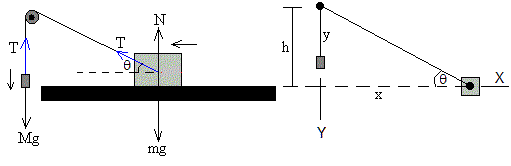
Situamos el origen en la polea y los ejes tal como indica la figura de la derecha, el eje Y apuntando hacia abajo

Dibujamos las fuerzas sobre cada uno de los dos cuerpos y aplicamos la segunda ley de Newton.

• Movimiento de las pesas

Las pesas situadas en un platillo se mueven verticalmente con una aceleración que es distinta de la aceleración del bloque.

${\displaystyle M\frac{d^{2}y}{d{t}^2}=Mg-T}$

• Movimiento del bloque

El bloque está en equilibrio en la dirección vertical

Tsinθ+N-mg=0

Donde la reacción del plano horizontal N tiene que ser una cantidad positiva, para que el bloque se mantenga deslizando

El bloque se mueve con aceleración a lo largo del plano horizontal

${\displaystyle m\frac{d^{2}x}{d{t}^2}=-T\cos \theta =-T\frac{x}{\sqrt{x^2+h^2}}}$

El máximo valor de la tensión T=Mg. El mínimo valor de N, cuando θ=π/2, es mg-T. Para que N>0, se tiene que cumplir que m>M

Eliminamos la tensión T para obtener la ecuación

${\displaystyle \frac{d^{2}x}{d{t}^2}=\frac{M}{m}\left(\frac{d^{2}y}{d{t}^2}-g\right)\frac{x}{\sqrt{x^2+h^2}}}$

En un instante dado t, el bloque dista x de la polea y las pesas se encuentran en la posición y por debajo de la polea. La relación entre x e y es

${\displaystyle l=\sqrt{x^2+h^2}+y}$

donde l es la longitud de la cuerda y h la altura de la polea sobre el plano horizontal.

Derivando con respecto del tiempo

${\displaystyle \frac{x}{\sqrt{x^2+h^2}}\frac{dx}{dt}+\frac{dy}{dt}=0}$

Para obtener la relación entre las aceleraciones d²x/dt² y d²y/dt², derivamos respecto del tiempo la relación anterior.

${\displaystyle \frac{h^2}{{\left(x^2+h^2\right)}^{3/2}}{\left(\frac{dx}{dt}\right)}^2+\frac{x}{\sqrt{x^2+h^2}}\frac{d^{2}x}{d{t}^2}+\frac{d^{2}y}{d{t}^2}=0}$

La ecuación del movimiento es

${\displaystyle \left(1+\frac{M}{m}\frac{x^2}{x^2+h^2}\right)\frac{d^{2}x}{d{t}^2}+\frac{M}{m}\left(g+\frac{h^2}{{\left(x^2+h^2\right)}^{3/2}}{\left(\frac{dx}{dt}\right)}^2\right)\frac{x}{\sqrt{x^2+h^2}}=0}$

Para determinar la posición x del bloque en función del tiempo t, tenemos que resolver una ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales en el instante t=0, x=x₀, dx/dt=0, parte del reposo.

La posición y de las pesas es

${\displaystyle y=l-\sqrt{x^2+h^2}}$

Cuando no hay rozamiento, la energía se conserva. La energía inicial es E₀=-Mgy₀. El nivel cero de energía potencial se sitúa en la polea

La energía en el instante t es la potencial de las pesas y las cinéticas del bloque y las pesas

${\displaystyle E=-Mgy+\frac{1}{2}m{\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}M{\left(\frac{dy}{dt}\right)}^2}$

La conservación de la energía nos permite verificar si el procedimiento numérico, produce buenos resultados.

Consideremos el siguiente sistema

• Masa del bloque, m=1 kg
• Masa de las pesas que cuelgan, M=0.8 kg
• Longitud de la cuerda, l=1.5 m
• Altura de la polea sobre el plano horizontal, h=1 m
• Posición inicial del bloque, x₀=0.8 m

Se representa la posición x del bloque y la posición y de las pesas en función del tiempo t.

function  arrastra_2()
    m=1; %bloque
    M=0.8; %pesas
    h=1; %altura polea
    l=1.5; %longitud cuerda
    x0=0.8;
    [t,x]=ode45(@aceleracion,[0,5.4],[x0,0]);
    y=l-sqrt(x(:,1).^2+h^2);
    plot(t,x(:,1),t,y) %tiempo t, posición y
    grid on
    xlabel('t')
    ylabel('x,y');
    legend('x','y','location','best')
    title('Movimiento')
    %conservación de la energía
    y0=l-sqrt(x0^2+h^2);
    E0=-M*9.8*y0;
    vy=-(x(:,1).*x(:,2))./sqrt(x(:,1).^2+h^2);
    E=-M*9.8*y+M*vy.^2/2+m*x(:,2).^2/2;
    disp(E0)
    disp(E)
    
   function z=aceleracion(~,x)
       a=(M/m)*x(1)^2/(x(1)^2+h^2)+1;
       b=-(M/m)*(9.8+h^2*x(2)^2/(x(1)^2+h^2)^(3/2))*x(1)/sqrt(x(1)^2+h^2);
       z=[x(2); b/a]; 
   end 
end

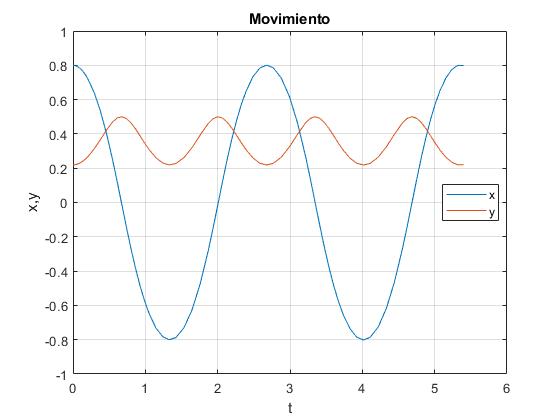
Mientras bloque se desplaza desde x₀ a x=0, las pesas se desplazan desde
$y_0=l-\sqrt{x_0^2+h^2}$, a y=l-h. Un cuarto de periodo después el bloque se encuentra en -x₀ y las pesas en y₀

Comprobamos la conservación de la energía

    -1.7199 %incial E0

    -1.7199 
    -1.7199 %en el instante t, E
   ...
   -1.7093
   -1.7094

El procedimiento numérico ode45 en este caso, no produce excelentes resultados como en otras ocasiones

Con rozamiento

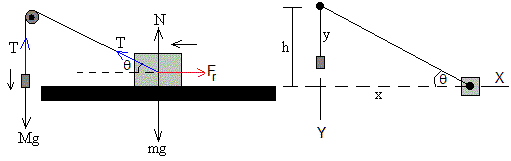
Cuando hay rozamiento, la fuerza de rozamiento F_r=μ_kN, se opone al movimiento del bloque. Cuando el bloque se mueve a lo largo del eje X hacia la izquierda (dx/dt<0) la fuerza de rozamiento apunta hacia la derecha, es positiva. Cuando se mueve hacia la derecha (dx/dt>0) es negativa

${\displaystyle \begin{array}{l}N=mg-T\sin \theta \\ m\frac{d^{2}x}{d{t}^2}=-T\cos \theta +F_r\\ m\frac{d^{2}x}{d{t}^2}=-T\frac{x}{\sqrt{x^2+h^2}}-{\mu }_k\left(mg-T\frac{h}{\sqrt{x^2+h^2}}\right)·\mathrm{sgn}\left(\frac{dx}{dt}\right)\end{array}}$

La función sgn(dx/dt) determina el signo de la velocidad del bloque.

Eliminamos la tensión T en las ecuaciones del movimiento

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=-T\frac{x}{\sqrt{x^2+h^2}}-{\mu }_k\left(mg-T\frac{h}{\sqrt{x^2+h^2}}\right)·\mathrm{sgn}\left(\frac{dx}{dt}\right)\\ M\frac{d^{2}y}{d{t}^2}=Mg-T\end{array}}$

Con la relación establecida en el apartado anterior entre las aceleraciones a la largo del eje X y a lo largo del eje Y, obtenemos

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=-\frac{M}{m}\left(g-\frac{d^{2}y}{d{t}^2}\right)\frac{x}{\sqrt{x^2+h^2}}-{\mu }_k\left(g-\frac{M}{m}\left(g-\frac{d^{2}y}{d{t}^2}\right)\frac{h}{\sqrt{x^2+h^2}}\right)·\mathrm{sgn}\left(\frac{dx}{dt}\right)\\ \frac{d^{2}x}{d{t}^2}=-g{\mu }_k\mathrm{sgn}\left(\frac{dx}{dt}\right)+\left(g-\frac{d^{2}y}{d{t}^2}\right)\frac{M}{m}\frac{\left(-x+h{\mu }_k\mathrm{sgn}\left(\frac{dx}{dt}\right)\right)}{\sqrt{x^2+h^2}}\\ \frac{d^{2}x}{d{t}^2}=-g{\mu }_k\mathrm{sgn}\left(\frac{dx}{dt}\right)+\left(g+\frac{h^2}{{\left(x^2+h^2\right)}^{3/2}}{\left(\frac{dx}{dt}\right)}^2+\frac{x}{\sqrt{x^2+h^2}}\frac{d^{2}x}{d{t}^2}\right)\frac{M}{m}\frac{\left(-x+h{\mu }_k\mathrm{sgn}\left(\frac{dx}{dt}\right)\right)}{\sqrt{x^2+h^2}}\end{array}}$

La ecuación diferencial que describe el movimiento del bloque es

${\displaystyle \left(1+\frac{M}{m}\frac{x\left(x-h{\mu }_k\mathrm{sgn}\left(\frac{dx}{dt}\right)\right)}{x^2+h^2}\right)\frac{d^{2}x}{d{t}^2}+g{\mu }_k\mathrm{sgn}\left(\frac{dx}{dt}\right)+\left(g+\frac{h^2}{{\left(x^2+h^2\right)}^{3/2}}{\left(\frac{dx}{dt}\right)}^2\right)\frac{M}{m}\frac{\left(x-h{\mu }_k\mathrm{sgn}\left(\frac{dx}{dt}\right)\right)}{\sqrt{x^2+h^2}}=0}$

La posición y de las pesas es

${\displaystyle y=l-\sqrt{x^2+h^2}}$

Comprobamos que cuando μ_k=0, (no hay rozamiento), obtenemos la ecuación del movimiento del apartado anterior

Cuando se detiene (la velocidad es nula pero no lo es la aceleración) se calcula la tensión T de la cuerda a partir de la ecuación del movimiento del bloque. Se comprueba si la componente horizontal de la tensión de la cuerda Tcosθ supera el máximo valor de la fuerza de rozamiento μ_sN=μ_s(mg-Tsinθ) en cuyo caso el movimiento del bloque continúa. En caso contario, el bloque se detiene

Energías

Se ha tomado como nivel cero de energía potencial, la altura 2h-l de la posición y=l-h de las pesas, cuando el bloque se encuentra en el origen x=0

• Energía potencial cuando la posición de las pesas es y, E_p=Mg(l-h-y). Cuando y=l-h la energía potencial E_p es nula

• La energía cinética del bloque es

${\displaystyle E_k=\frac{1}{2}m{\left(\frac{dx}{dt}\right)}^2}$

• La energía cinética de las pesas es

${\displaystyle E_k=\frac{1}{2}M{\left(\frac{dy}{dt}\right)}^2=\frac{1}{2}M{\left(\frac{x}{\sqrt{x^2+h^2}}\frac{dx}{dt}\right)}^2}$

La suma de las tres contribuciones es la energía E del sistema

La energía inicial, es la potencial de las pesas cuando el bloque se ha desplazado a x₀

${\displaystyle E_0=Mg\left(\sqrt{x_0^2+h^2}-h\right)}$

La diferencia E-E₀ es el trabajo de la fuerza de rozamiento

Actividades

Se introduce

• La masa del las pesas que cuelgan M, en el control titulado Masa pesas
• La masa del bloque se ha fijado en m=1 kg
• El coeficiente de rozamiento μ_s=μ_k, en el control titulado Coef. rozamiento
• La posición inicial del bloque, x₀ en el control titulado Posición
• La longitud de la cuerda se ha fijado en l=1.5 m
• La altura de la polea se ha fijado en h=1 m

El bloque no se puede desplazar hacia la derecha más de $x_0=\sqrt{l^2-h^2}$

El programa interactivo muestra el balance energético

La energía E se divide en dos sectores: energía potencial (sector azul) de las pesas y la cinética (sector rojo) del bloque y las pesas . El radio del círculo que representa la energía total E va disminuyendo. Parte de la energía inicial E₀ se va transformando en trabajo de la fuerza de rozamiento (en color negro)

En la parte superior derecha, se porporcionan los datos de

• El tiempo t
• La posición x del bloque
• La velocidad dx/dt del bloque
• La posición y de las pesas

Referencias

H J Herrera Suárez, M Machado-Higuera, J H Muñoz. Two blocks connected by a string with variable tension: a dynamic case. Phys. Educ. 55 (2020) 055022

Carl E Mungan. Comment on 'Two blocks connected by a string with variable tension: a dynamic case'. Phys. Educ. 56 (2021) 028001