En el laboratorio disponemos de una pista de aluminio, por el que va a circular un cochecito que tiene imanes adosados a uno de los frontales tal como se muestra en la fotografía. Un sensor de movimiento (dispositivo de color azul) situado en un extremos de la pista y comunicado con el ordenador a través del puesto USB, toma datos de la posición del cochecito en función del tiempo a la frecuencia seleccionada. El programa CAPSTONE de PASCO representa gráficamente la posición, la velocidad o aceleración del móvil en función del tiempo

Debido a las corrientes de Foucault que los imanes originan en la pista de aluminio a medida que se mueve el cochecito, la fuerza que ejerce el campo magnético sobre las corrientes inducidas en la pista, originan una fuerza de rozamiento proporcional a la velocidad del cochecito F_r=k·v. Supondremos que la fuerza de rozamiento en las ruedas del cochecito es pequeña

Pista horizontal

Colocamos el cochecito sobre una pista horizontal, le damos un impulso inicial y observamos cómo la velocidad disminuye con el tiempo hasta que se detiene

Ajustando la altura de los tres potentes imanes de modo que se mantengan paralelos a la pista, aumentamos o diminuimos la fuerza de rozamiento

Las fuerza que actúan sobre el cuerpo de masa m son:

• El peso mg
• La reacción N del plano horizontal
• la fuerza de rozamiento F_r=kv

Como hay equilibrio en la dirección vertical, las dos primeras son iguales y de sentido contrario, N=mg, y no afectan al movimiento horizontal del cuerpo. La ecuación del movimiento del cochecito de masa m es

${\displaystyle m\frac{dv}{dt}=-kv}$

Integramos la ecución diferencial con las siguientes condiciones inciales, en el instante t=0, la velocidad inicial del cochecito es v₀

${\displaystyle \begin{array}{l}\frac{dv}{v}=-\frac{k}{m}dt\\ {\displaystyle \underset{v_0}{\overset{v}{\int }}\frac{dv}{v}}=-\frac{k}{m}{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ \ln v-\ln v_0=-\frac{k}{m}t\\ v=v_0\exp \left(-\frac{k}{m}t\right)\end{array}}$

k_m=0.2;
v0=1;
v=@(t) v0*exp(-k_m*t);
fplot(v,[0,25])
grid on
xlabel('t')
ylabel('v')
title('Fuerza de rozamiento proporcional a la velocidad')

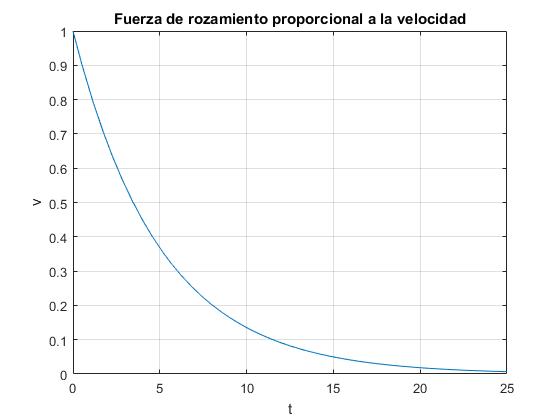
La velocidad disminuye exponencialmente con el tiempo hasta que después de un cierto tiempo (teóricamente infinito) se detiene. En la experiencia real, el rozamiento mecánico no es nulo, por lo que el cochecito se detiene en un tiempo finito

Volvemos a integrar para calcular la posición x del móvil en función del tiempo, sabiendo que en el instante t=0, parte del origen, x=0

${\displaystyle \begin{array}{l}x-x_0={\displaystyle \underset{t_0}{\overset{t}{\int }}v·dt}\\ x={\displaystyle \underset{0}{\overset{t}{\int }}{v}_0\exp \left(-\frac{k}{m}t\right)dt}\\ x=\frac{m}{k}{v}_0\left(1-\exp \left(-\frac{k}{m}t\right)\right)\end{array}}$

k_m=0.2;
v0=1;
x=@(t) v0*(1-exp(-k_m*t))/k_m;
fplot(x,[0,25])
grid on
xlabel('t')
ylabel('x')
title('Fuerza de rozamiento proporcional a la velocidad')

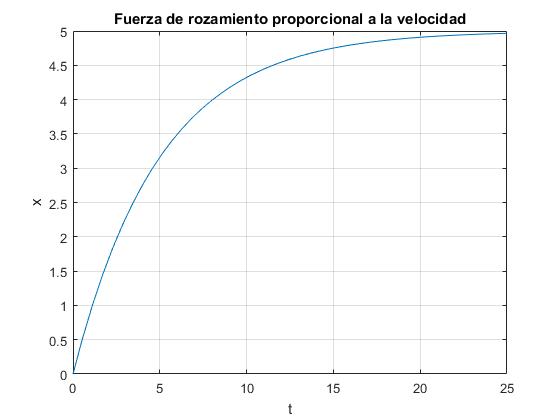
El móvil se detiene en una posición mv₀/k, después de un tiempo muy grande. En el ejemplo es x_∞=1/0.2=5

Pista inclinada

Inclinamos la pista un pequeño ángulo y dejamos caer el cochecito, observamos que el cochecito adquiere una velocidad final constante

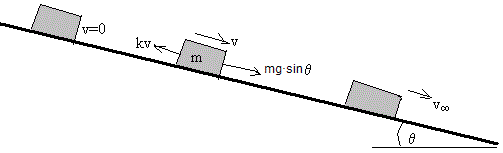
Las fuerza que actúan sobre el cuerpo de masa m son:

• El peso mg
• La reacción N del plano horizontal
• la fuerza de rozamiento F_r

Como hay equilibrio en la dirección perpendicular al plano, N=mgcosθ, y no afectan al movimiento horizontal del cuerpo. La ecuación del movimiento del cochecito de masa m es

${\displaystyle m\frac{dv}{dt}=F-kvF=mg\sin \theta }$

Integramos la ecuación diferencial con las siguientes condiciones inciales, en el instante t=0, la velocidad inicial del cochecito es v=0

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{v}{\int }}\frac{mdv}{F-kv}}={\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ v=\frac{F}{k}\left(1-\exp \left(\frac{-kt}{m}\right)\right)v_{\infty }=\frac{F}{k}\end{array}}$

Esta ecuación nos dice que se alcanza la velocidad límite v_∞ después de un tiempo teóricamente infinito. Si representamos v en función del tiempo t la gráfica tiene una asíntota horizontal en v=v_∞.

k_m=0.2;
theta=30*pi/180;
v=@(t) 9.8*sin(theta)*(1-exp(-k_m*t))/k_m;
fplot(v,[0,25])
grid on
xlabel('t')
ylabel('v')
title('Fuerza de rozamiento proporcional a la velocidad')

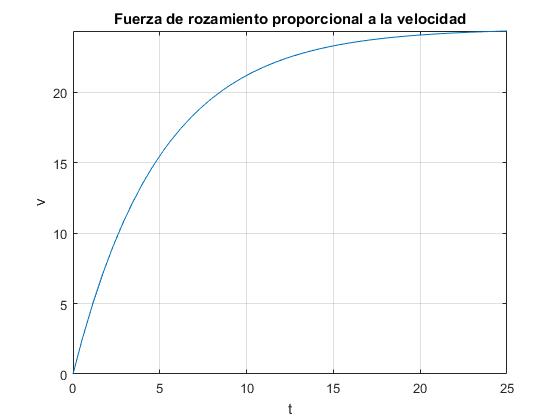
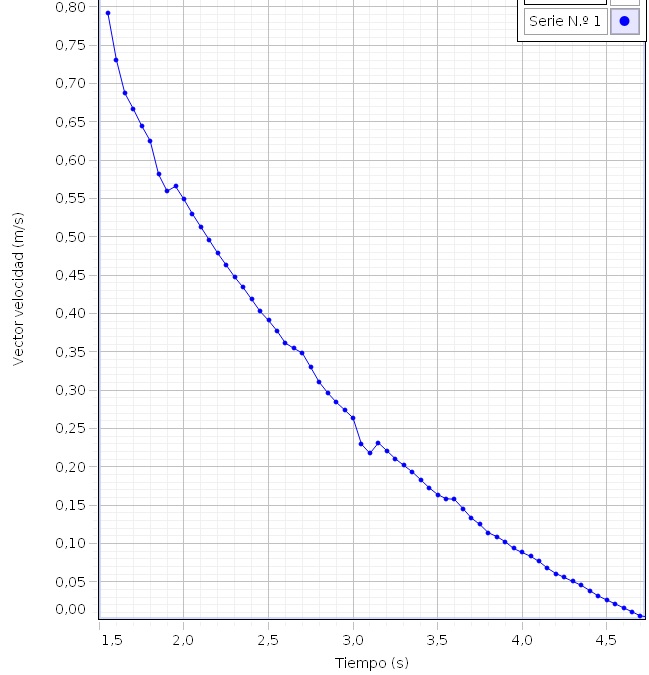
En la experiencia real, el rozamiento mecánico no es nulo, por lo que el cochecito alcanza la velocidad límite máxima y luego, va disminuyendo

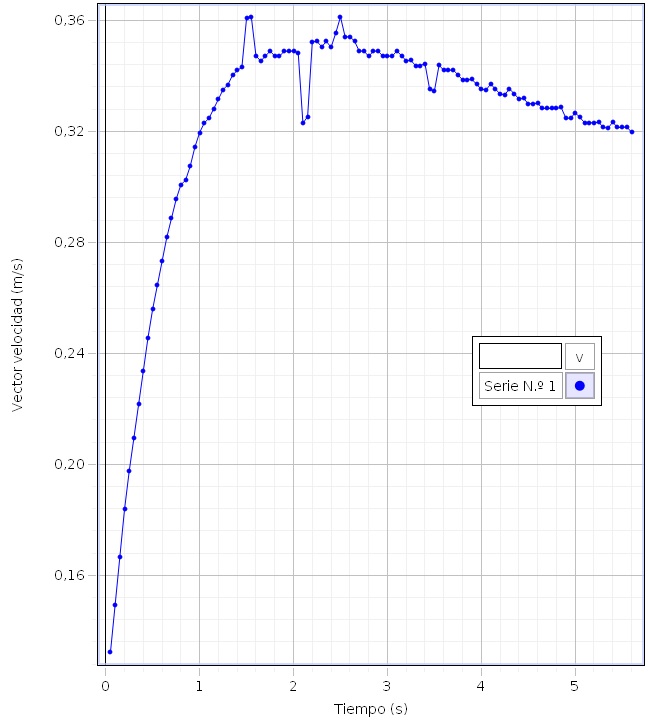
Integrando, obtenemos la posición x del móvil en función del tiempo, sabiendo que en el instante t=0, parte del origen, x=0

${\displaystyle \begin{array}{l}\frac{mdv}{F-kv}=dt\\ {\displaystyle \underset{0}{\overset{v}{\int }}\frac{mdv}{F-kv}}={\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ -\frac{m}{k}\ln \left(F-kv\right)+\frac{m}{k}\ln \left(F\right)=t\\ v=\frac{F}{k}\left(1-\exp \left(-\frac{k}{m}t\right)\right)\end{array}}$

k_m=0.2;
theta=30*pi/180;
x=@(t) 9.8*sin(theta)*(t-(1-exp(-k_m*t))/k_m)/k_m;
fplot(x,[0,25])
grid on
xlabel('t')
ylabel('x')
title('Fuerza de rozamiento proporcional a la velocidad')

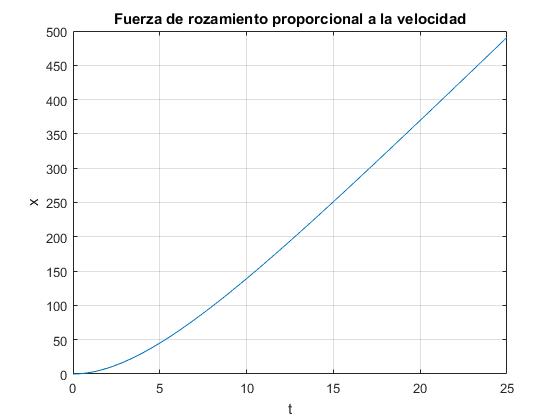
Después de un cierto tiempo, la velocidad es casi constante y el movimiento es rectilíneo uniforme.

${\displaystyle x=\frac{F}{k}\left(t-\frac{m}{k}\right)}$

Tratamiento de los datos de la experiencia

CAPSTONE nos suministra un fichero de texto con el tiempo t y la posición x medidas por el sensor de movimiento. Este fichero lo editamos y lo preparamos para ser importado por MATLAB. Eliminamos la cabecera y sustituímos el separador de la parte decimal, una coma, por un punto. MATLAB convierte el fichero en una matriz de dos columnas. Renombramos en la ventana Workspace, la variable con el nombre de datos

Ajustamos los datos del primer fichero a la función

${\displaystyle x=a\left(1-\exp \left(-bt\right)\right)}$

t=datos(:,1)-datos(1,1);
x=datos(:,2)-datos(1,2);
hold on
plot(t,x,'ro','markersize',3,'markerfacecolor','r')
f=@(a,t) a(1)*(1-exp(-a(2)*t));      
a0=[1,1];  %valor inicial
af=nlinfit(t,x,f,a0);
g=@(t) f(af,t);
fplot(g,[t(1),t(end)])
title('Ajuste no lineal, y=a*(1-exp(-b·t)')
xlabel('t')
ylabel('x')
grid on
hold off 

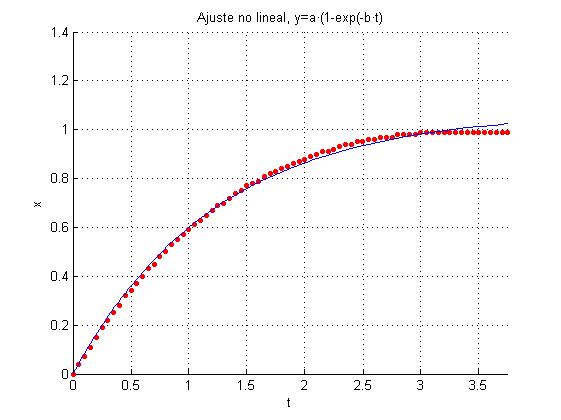
Los parámetros a y b valen, respectivamente

>> af
af =    1.2482    0.6705

Ajustamos los datos del segundo fichero a la función

${\displaystyle x=at-\frac{a}{b}\left(1-\exp \left(-bt\right)\right)}$

El parámetro a es la velocidad límite constante

t=datos(:,1)-datos(1,1);
x=datos(:,2)-datos(1,2);
hold on
plot(t,x,'ro','markersize',3,'markerfacecolor','r')
f=@(a,t) a(1)*t-a(1)*(1-exp(-a(2)*t))/a(2);      
a0=[1,1];  %valor inicial
af=nlinfit(t,x,f,a0);
g=@(t) f(af,t);
fplot(g,[t(1),t(end)])
title('Ajuste no lineal, y=a*t-a*(1-exp(-b·t))/b')
xlabel('t')
ylabel('x')
grid on
hold off  

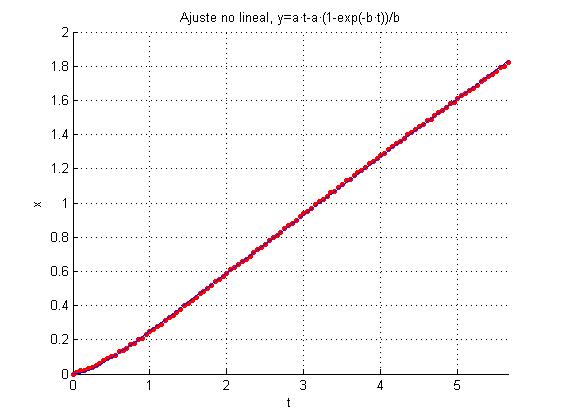
Los parámetros a y b valen, respectivamente

>> af
af =    0.3406    3.7430

Actividades

Cuando se carga el programa se genera un número aleatorio que representa el cociente k/m

Se activa el botón de radio titulado Horizontal o Inclinado

• Con el plano horizontal, se puede cambiar la velocidad inicial v₀ en el control titulado Velocidad
• Con el plano inclinado, se puede cambiar el ángulo que hace el plano con la horizontal en el control titulado Angulo

Se pulsa el botón titulado Nuevo

Observamos el movimiento del cochecito y a la derecha, se representa su velocidad en función del tiempo

Fuerza de rozamiento proporcional a vⁿ

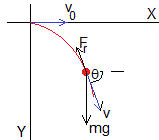
Se lanza una partícula de masa m desde lo alto de una colina con velocidad horizontal v₀

Supondremos que además del peso, mg, la partícula experimenta una fuerza de rozamiento proporcional a la velocidad F_r=k·vⁿ, de la misma dirección pero de sentido contario

Las ecuaciones del movimiento de la partícula son

${\displaystyle \begin{array}{l}\{\begin{array}{l}m\frac{d{v}_x}{dt}=-k{v}^n\cos \theta \\ m\frac{d{v}_y}{dt}=mg-k{v}^n\sin \theta \end{array}\\ \{\begin{array}{l}m\frac{d{v}_x}{dt}=-k{v}^n\frac{v_x}{v}\\ m\frac{d{v}_y}{dt}=mg-k{v}^n\frac{v_y}{v}\end{array}\end{array}}$

La componente v_x de la velocidad va disminuyendo, la componente v_y de la velocidad tiende hacia un valor límite constante, el ángulo de la velocidad con la horizontal, θ tiende hacia π/2

Escribimos las ecuaciones del movimiento en términos de variables adimensionales

${\displaystyle \begin{array}{l}k{v}_t^n=mg\\ \tau =\frac{gt}{v_t},V_x=\frac{v_x}{v_t},V_y=\frac{v_y}{v_t},V=\frac{\sqrt{v_x^2+v_y^2}}{v_t}\\ \{\begin{array}{l}\frac{d{V}_x}{d\tau }=-V^{n-1}{V}_x\\ \frac{d{V}_y}{d\tau }=1-V^{n-1}{V}_y\end{array}\end{array}}$

Expresamos el módulo de la velocidad adimensional V en función del ángulo 0≤θ≤π/2

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{d\left(V\cos \theta \right)}{d\tau }=-V^n\cos \theta \\ \frac{d\left(V\sin \theta \right)}{d\tau }=1-V^n\sin \theta \end{array}\\ \{\begin{array}{l}\frac{dV}{d\tau }\cos \theta -V\sin \theta \frac{d\theta }{d\tau }=-V^n\cos \theta \\ \frac{dV}{d\tau }\sin \theta +V\cos \theta \frac{d\theta }{d\tau }=1-V^n\sin \theta \end{array}\end{array}}$

En este sistema de dos ecuaciones, despejamos dV/dτ y dθ/dτ

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{dV}{d\tau }=\sin \theta -V^n\\ V\frac{d\theta }{d\tau }=\cos \theta \end{array}\\ \frac{1}{V}\frac{dV}{d\theta }=\frac{\sin \theta -V^n}{\cos \theta }\\ \frac{dV}{d\theta }=V\tan \theta -\frac{V^{n+1}}{\cos \theta }\end{array}}$

Hacemos el cambio de variable

${\displaystyle \begin{array}{l}z=\frac{1}{V^n},dz=-n{V}^{-n-1}dV=-n\frac{z}{V}·dV\\ -\frac{V}{nz}\frac{dz}{d\theta }=V\tan \theta -\frac{V}{z\cos \theta }\\ \frac{dz}{d\theta }+nz\tan \theta =\frac{n}{\cos \theta }\end{array}}$

Resolvemos esta ecuación diferencial del tipo

${\displaystyle \frac{dx}{dt}+P(t)x=Q(t)}$

La solución de la ecuación diferencial homogénea es

${\displaystyle \begin{array}{l}\frac{dz}{d\theta }+nz\tan \theta =0\\ \frac{dz}{z}=-n\frac{\sin \theta }{\cos \theta }d\theta \\ {\displaystyle \int \frac{dz}{z}=-n{\displaystyle \int \frac{\sin \theta }{\cos \theta }d\theta }}\\ \ln z=n\ln \left(\cos \theta \right)+C\\ z=C\left(\theta \right)·{\cos }^n\theta \end{array}}$

Se introduce esta solución en la ecuación diferencial no homogénea

${\displaystyle \begin{array}{l}z=C\left(\theta \right)·{\cos }^n\theta \\ \frac{dz}{d\theta }+nz\tan \theta =\frac{n}{\cos \theta }\\ {\cos }^n\theta \frac{dC}{d\theta }-nC{\cos }^{n-1}\theta \sin \theta +nC{\cos }^n\theta \frac{\sin \theta }{\cos \theta }=\frac{n}{\cos \theta }\\ {\cos }^n\theta \frac{dC}{d\theta }=\frac{n}{\cos \theta }\\ dC=\frac{n}{{\cos }^{n+1}\theta }d\theta \\ C\left(\theta \right)=n{\displaystyle \int \frac{d\theta }{{\cos }^{n+1}\theta }+c}\end{array}}$

El resultado es

${\displaystyle z=\left(n{\displaystyle \int \frac{d\theta }{{\cos }^{n+1}\theta }+c}\right){\cos }^n\theta }$

La condición inicial es, θ=0, z=z₀

${\displaystyle z=\left(n{\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{d\theta }{{\cos }^{n+1}\theta }+z_0}\right){\cos }^n\theta }$

Casos particulares

• n=1

Calculamos la integral

${\displaystyle {\displaystyle \int \frac{d\theta }{{\cos }^2\theta }}=\tan \theta }$

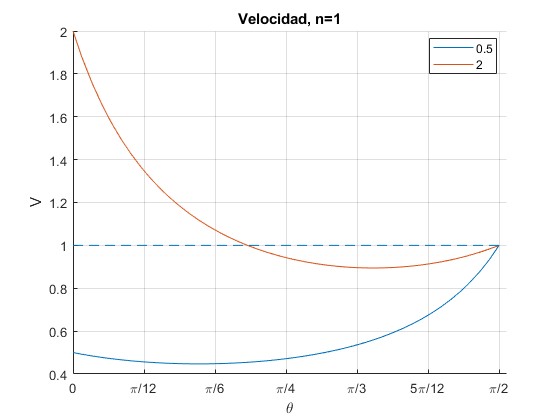
El módulo de la velocidad V es

${\displaystyle \begin{array}{l}z=\left({\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{d\theta }{{\cos }^2\theta }+z_0}\right)\cos \theta \\ z=\left(\tan \theta +z_0\right)\cos \theta \\ \frac{1}{V}=\sin \theta +\frac{1}{V_0}\cos \theta \\ V=\frac{V_0}{V_0\sin \theta +\cos \theta }\end{array}}$

Representamos el módulo de la velocidad V en función del ángulo θ para las velocidades iniciales V₀=0.5 y 2.0

hold on
for V0=[0.5,2.0]
    fplot(@(x) V0./(V0*sin(x)+cos(x)), [0,pi/2])
end
line([0,pi/2],[1,1],'lineStyle','--')
hold off
grid on
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
legend('0.5','2','location','best')
xlabel('\theta')
ylabel('V')
title ('Velocidad, n=1')



• n=2

Conocido el resultado de la integral

${\displaystyle {\displaystyle \int \frac{dx}{\cos x}}=\ln \left(\left|\frac{1+\sin x}{\cos x}\right|\right)}$

Calculamos la integral

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{d\theta }{{\cos }^3\theta }},\{\begin{array}{l}u=\frac{1}{\cos \theta },du=\frac{\sin \theta }{{\cos }^2\theta }d\theta \\ dv=\frac{d\theta }{{\cos }^2\theta },v=\tan \theta \end{array}\\ =\frac{\tan \theta }{\cos \theta }-{\displaystyle \int \frac{{\sin }^2\theta }{{\cos }^3\theta }d\theta }=\frac{\tan \theta }{\cos \theta }-{\displaystyle \int \frac{1-{\cos }^2\theta }{{\cos }^3\theta }d\theta }=\frac{\tan \theta }{\cos \theta }-{\displaystyle \int \frac{d\theta }{{\cos }^3\theta }}+{\displaystyle \int \frac{d\theta }{\cos \theta }}\\ 2{\displaystyle \int \frac{d\theta }{{\cos }^3\theta }}=\frac{\sin \theta }{{\cos }^2\theta }+\ln \left(\frac{1+\sin \theta }{\cos \theta }\right)\end{array}}$

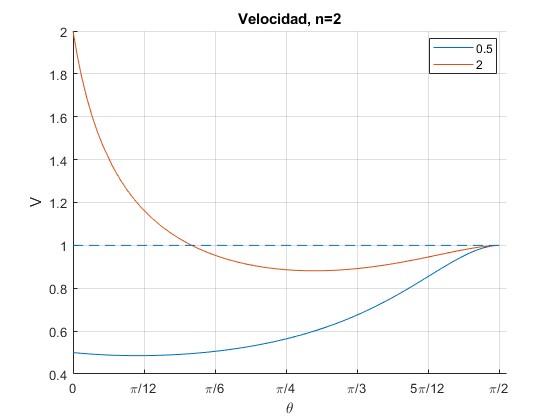
El módulo de la velocidad V es

${\displaystyle \begin{array}{l}z=\left(2{\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{d\theta }{{\cos }^3\theta }+z_0}\right){\cos }^2\theta \\ z=\left(2\left(\frac{1}{2}\frac{\sin \theta }{{\cos }^2\theta }+\frac{1}{2}\ln \left(\frac{1+\sin \theta }{\cos \theta }\right)\right)+z_0\right){\cos }^2\theta \\ \frac{1}{V^2}=\sin \theta +{\cos }^2\theta ·\ln \left(\frac{1+\sin \theta }{\cos \theta }\right)+\frac{{\cos }^2\theta }{V_0^2}\end{array}}$

Representamos el módulo de la velocidad V en función del ángulo θ para las velocidades iniciales V₀=0.5 y 2.0

hold on
for V0=[0.5,2]
    V=@(x) 1./sqrt(sin(x)+(cos(x).^2).*log((1+sin(x))./cos(x))+cos(x).^2/V0^2);
    fplot(V, [0,pi/2])
end
line([0,pi/2],[1,1],'lineStyle','--')
hold off
grid on
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
legend('0.5','2','location','best')
xlabel('\theta')
ylabel('V')
title ('Velocidad, n=2')



• n=3

Calculamos la integral

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{d\theta }{{\cos }^4\theta }},\{\begin{array}{l}u=\frac{1}{{\cos }^2\theta },du=\frac{2\sin \theta }{{\cos }^3\theta }d\theta \\ dv=\frac{d\theta }{{\cos }^2\theta },v=\tan \theta \end{array}\\ =\frac{\tan \theta }{{\cos }^2\theta }-2{\displaystyle \int \frac{{\sin }^2\theta }{{\cos }^4\theta }d\theta }=\frac{\tan \theta }{{\cos }^2\theta }-2{\displaystyle \int \frac{1-{\cos }^2\theta }{{\cos }^4\theta }d\theta }=\frac{\tan \theta }{{\cos }^2\theta }-2{\displaystyle \int \frac{d\theta }{{\cos }^3\theta }}+2{\displaystyle \int \frac{d\theta }{{\cos }^2\theta }}\\ 3{\displaystyle \int \frac{d\theta }{{\cos }^4\theta }}=\frac{\sin \theta }{{\cos }^3\theta }+2\tan \theta \end{array}}$

El módulo de la velocidad V es

${\displaystyle \begin{array}{l}z=\left(3{\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{d\theta }{{\cos }^4\theta }+z_0}\right){\cos }^3\theta \\ z=\left(3\left(\frac{1}{3}\frac{\sin \theta }{{\cos }^3\theta }+\frac{2}{3}\tan \theta \right)+z_0\right){\cos }^3\theta \\ \frac{1}{V^2}=\sin \theta +2\sin \theta {\cos }^2\theta +\frac{{\cos }^3\theta }{V_0^2}\end{array}}$

Representamos el módulo de la velocidad V en función del ángulo θ para las velocidades iniciales V₀=1.05 y 0.95

hold on
for V0=[1.05,0.95]
    V=@(x) 1./sqrt(sin(x)+2*sin(x).*(cos(x).^2)+cos(x).^3/V0^2);
    fplot(V, [0,pi/2])
end
line([0,pi/2],[1,1],'lineStyle','--')
hold off
grid on
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
legend('1.05','0.95','location','best')
xlabel('\theta')
ylabel('V')
title ('Velocidad, n=3')



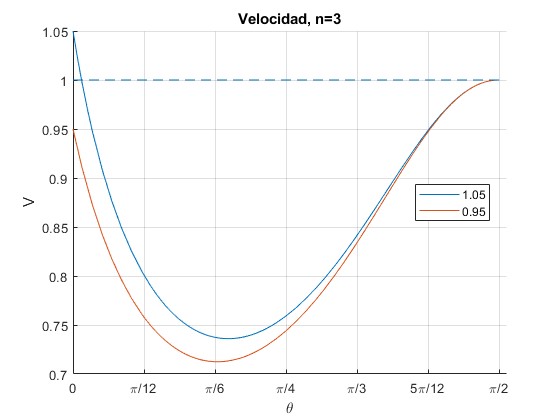
La velocidad de la partícula disminuye y luego, vuelve a aumentar hasta alcanzar la velocidad límite

Referencias

E.N. Miranda, S. Nikolskaya, R. Riba. Minimum and terminal velocities in projectile motion. Revista Brasileira de Ensino de Física. V. 26, n° 2, pp. 125 - 127, (2004)