Medida del coeficiente estático.
Un cuerpo A cuelga de una cuerda que pasa a través de una polea de masa despreciable y que está unida a un bloque B que puede deslizar a lo largo de un plano horizontal. Sobre el bloque B se coloca un cuerpo C. Se supone que el rozamiento entre el cuerpo B y el plano horizontal es despreciable. Mientras que existe un rozamiento entre el cuerpo C y el cuerpo B.
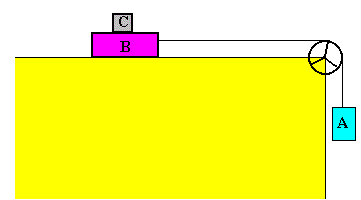
En la figura, vemos el diagrama de fuerzas, a partir del cual obtenemos las ecuaciones del movimiento de cada uno de los cuerpos en las distintas situaciones
Cuando el cuerpo C está en reposo sobre el cuerpo B.
Cuando el cuerpo C va a empezar a deslizar sobre el cuerpo B
Cuando el cuerpo C desliza sobre el cuerpo B
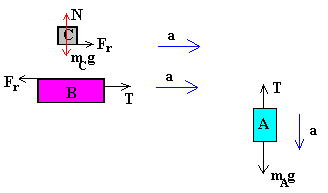
Ambos tienen la misma aceleración a que la del cuerpo A
Movimiento del cuerpo A
mAg-T=mA·a
Movimiento del cuerpo B
T-Fr=mB·a
Movimiento del cuerpo C
Fr=mC·a
La fuerza de rozamiento Fr es la que hace que el cuerpo C se mueva con el cuerpo B: el cuerpo B ejerce una fuerza Fr sobre el cuerpo C dirigida hacia la derecha. Por el Principio de Acción y Reacción el cuerpo C ejerce una fuerza igual y de sentido contrario sobre el cuerpo B.
De éstas ecuaciones obtenemos la aceleración a y la fuerza Fr de rozamiento entre los cuerpos B y C.
Cuando Fr=mC·a alcance el valor máximo μs·N o bien, μs·mC·g, el cuerpo C va a empezar a deslizar sobre el cuerpo B. μs es el coeficiente estático.
Incrementando la masa de A, incrementamos la aceleración, en el momento en el que el cuerpo C va a empezar a deslizar se cumple que
a=μsg
Calculamos la aceleración crítica a, a partir de los valores de las masas mA, mB y mC en la fórmula anterior y a continuación, obtenemos el valor del coeficiente estático.
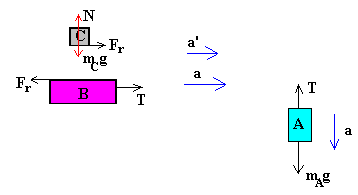
Cuando se incrementa aún más la masa de A, se incrementa la aceleración a, el cuerpo C desliza sobre el cuerpo B, el valor de la fuerza de rozamiento disminuye y vale ahora
Fr=μkmC·g
Donde μk es el coeficiente de rozamiento por deslizamiento.
Las aceleraciones a del cuerpo B y la aceleración a' del cuerpo C ya no son las mismas
Movimiento del cuerpo A, mAg-T=mA·a
Movimiento del cuerpo B, T-Fr=mB·a
Movimiento del cuerpo C, Fr=mC·a’
Fuerza de rozamiento, Fr=μk·mC·g
Como la aceleración a de B, es mayor que la aceleración a’ de C, la aceleración relativa de C respecto de B, es a’-a. Desde el punto de vista de un observador situado en B, el cuerpo C se mueve hacia atrás con una aceleración |a’-a|.
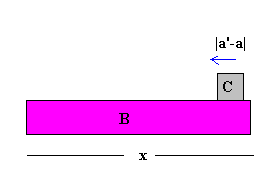
El cuerpo C tarda en llegar al final del cuerpo B un tiempo t, dado por
donde x es la distancia recorrida del cuerpo C sobre el cuerpo B.
La velocidad con respecto al Laboratorio del cuerpo C cuando abandona el cuerpo B será
donde t es el tiempo que C está deslizando sobre B.
En el momento en el que el cuerpo C abandona el bloque B, la aceleración del sistema formado por los bloques A y B cambia,
Movimiento del cuerpo A, mAg-T=mA·a
Movimiento del cuerpo B, T=mB·a
El cuerpo C abandona el cuerpo B
- El cuerpo C desliza sobre el plano horizontal
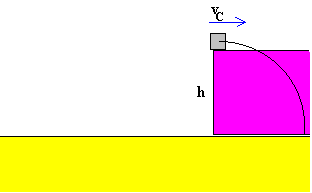
Ahora el cuerpo C que tiene una velocidad inicial vC dirigida hacia la derecha, se mueve bajo la sola influencia de su peso. Describe, por tanto, un movimiento curvilíneo bajo la aceleración constante de la gravedad, o un tiro parabólico.
El tiempo que tarda en llegar al plano horizontal es
donde h es la altura del bloque B.
La distancia que recorre horizontalmente es
x=vCt
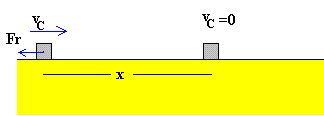
Una vez que el cuerpo C entra en contacto con el plano horizontal, sobre el cuerpo C actúa una fuerza de rozamiento que hace que se pare al cabo de un cierto tiempo.
Suponemos que la fuerza de rozamiento entre el plano horizontal y el bloque C, es la misma que entre el bloque C y el bloque B. El cuerpo C, con una velocidad inicial horizontal vC, se parará después de haber recorrido una distancia x, dada por
Ejemplos
Supongamos que los coeficientes de rozamiento son:
- Coeficiente estático μs=0.34
- Coeficiente cinético μk=0.25
Las masas de los bloques B y C están fijadas por el programa interactivo
- Masa del bloque B, mB=2.5 kg
- Masa del bloque C, mC=1.5 kg
La masa del bloque A se puede cambiar.
Ejemplo 1
Masa del bloque A, mA=1.3 kg
Observamos que el cuerpo C está en reposo sobre el cuerpo B, la aceleración vale
La fuerza de rozamiento Fr que hace que el cuerpo C se mueva con aceleración a es
Fr=mC·a=1.5·2.4=3.60 N
Que es inferior a la máxima μs·N=μs·mC·g=0.34·1.5·9.8=5.0 N
Ejemplo 2
Masa del bloque A, mA=6.3 kg
Si suponemos que el cuerpo C está en reposo sobre el cuerpo B, la aceleración vale
La fuerza de rozamiento Fr que que hace que el cuerpo C se mueva con aceleración a es
Fr=mC·a=1.5·5.99=8.99 N
Que como vemos es superior al máximo valor μs·N=μs·mC·g=0.34·1.5·9.8=5.0 N
-
El cuerpo C desliza sobre el bloque B.
-
El cuerpo C describe una trayectoria parabólica hasta que llega al suelo.
-
El cuerpo C desliza con rozamiento sobre el suelo hasta que se para.
La fuerza que actúa sobre el cuerpo C es la de rozamiento Fr= μk·N= μk·mC·g=0.25·1.5·9.8=3.67 N, y su aceleración vale a'= μk·g=0.25·9.8=2.45 m/s2
La aceleración de los bloques A y B valen ahora
El bloque C desliza hacia atrás con una aceleración de a-a'=4.15 m/s2 sobre el bloque B. Como el bloque B mide 0.5 m de largo, tarda un tiempo t1=0.49 s en abandonarlo con una velocidad de vC=a'·t1=2.45·0.49=1.20 m/s
En este tiempo el bloque B se habrá desplazado
y tendrá una velocidad de vB=a·t1=6.60·0.49=3.24 m/s
El cuerpo C se habrá desplazado
A partir de este instante, la aceleración del sistema formado por el bloque A y el B cambia y vale
Como la altura del bloque B es de 0.25 m el tiempo que tarda en llegar al suelo es t2=0.23 s.
El desplazamiento del cuerpo C en este tiempo será vC·t2=1.20·0.23=0.27 m
La posición del cuerpo C cuando toca el suelo será la suma de ambos desplazamientos
xC=0.30+0.27=0.57 m
Esta es la posición del cuerpo C en el instante t1+t2=0.49+0.23=0.72 s.
La velocidad inicial del cuerpo C es vC. El tiempo que tarda en parase
El desplazamiento del móvil C durante este tiempo es de 0.29 m
La posición de C en el instante t1+t2+t3=0.49+0.23+0.49=1.21 s. es
xC=0.57+0.29=0.86 m
El desplazamiento del bloque B desde el instante t1=0.49 s en el que se desprende el bloque C al instante t=1.21 s en el que se para el bloque C vale
La posición del cuerpo B será xB=0.79+4.15=4.94 m. Esta posición no aparece en la simulación ya que el máximo desplazamiento de B es de 2.3 m.
Ejemplo 3
Determinación del coeficiente estático
Se modifica la masa de A hasta observar que el bloque C comienza a moverse sobre el bloque B. Por ejemplo, observamos que el bloque C no se mueve cuando la masa de A, mA=2.0, y observamos que el bloque C se mueve cuando mA=2.1 kg.
Si refinamos un poco las medidas, veremos que el bloque C no se mueve cuando mA=2.05 y se mueve cuando mA=2.06.
La aceleración crítica del sistema tomando mA=2.05 es
El coeficiente estático valdrá entonces a=μsg, por lo que μs=0.34, que es el dato que nos ha suministrado el programa interactivo.
Actividades
Las masas de los bloques B y C vienen fijadas por el programa en 2.5 y 1.5 kg respectivamente. La masa de A se puede cambiar para modificar la aceleración del sistema. A continuación, se pulsa el botón Nuevo.
Si el bloque C no se mueve sobre el bloque B, incrementamos la masa de A y volvemos a pulsar el botón Nuevo y así sucesivamente, hasta que el bloque empiece a deslizar.
Activando la casilla titulada Fuerzas se representan los vectores fuerza que actúan sobre el bloque C . Apreciamos como aumenta la fuerza de rozamiento a medida que aumenta la aceleración del sistema mientras el bloque C está en reposo sobre el bloque B.
Cuando la fuerza de rozamiento alcanza el valor máximo, el bloque C empieza a deslizar sobre el bloque B, ambos bloques B y C tienen entonces distinta aceleración. El bloque C desliza hacia atrás visto por un observador situado en el bloque B.
Ejercicio
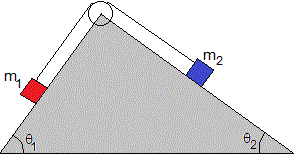
El sistema de la figura, está formado por dos partículas de masas m1 y m2 situadas sobre dos planos inclinados de ángulos θ1 y θ2, respectivamente. Las partículas están unidas por una cuerda inextensible y de masa despreciable que pasa por una polea ideal.
Los planos no son lisos, hay rozamiento entre las partículas y los planos inclinados, cuyo coeficiente estático es μs.
Las masas m1 y m2 se eligen de modo que el sistema está a punto de deslizar hacia la derecha
¿Cuanta masa Δm1 hemos de añadir a la a partícula de masa m1 para que el sistema esté a punto de deslizar hacia la izquierda?
Está a punto de deslizar hacia la derecha
- El peso, m1g
- La reacción del plano, N1=m1gcosθ1
- La fuerza de rozamiento, F1=μsN1=μsm1gcosθ1
- La tensión de la cuerda, T
- El peso, m2g
- La reacción del plano, N2=m2gcosθ2
- La fuerza de rozamiento, F2=μsN2=μsm2gcosθ2
- La tensión de la cuerda, T
Se añade la masa Δm1 para que esté a punto de deslizar hacia la izquierda
- El peso, (m1+Δm1)g
- La reacción del plano, N1=(m1+Δm1)gcosθ1
- La fuerza de rozamiento, F1=μsN1=μs(m1+Δm1)gcosθ1
- La tensión de la cuerda, T
- El peso, m2g
- La reacción del plano, N2=m2gcosθ2
- La fuerza de rozamiento, F2=μsN2=μsm2gcosθ2
- La tensión de la cuerda, T
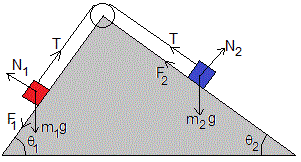
Las fuerzas sobre la partícula de masa m1 son
En la situación de equilibrio
Las fuerzas sobre la partícula de masa m2 son
En la situación de equilibrio
Eliminando la tensión, T
Llamamos μs=tanλ
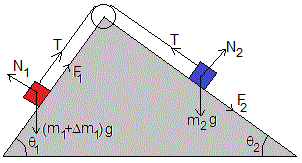
Las fuerzas sobre la partícula de masa m1+Δm1, son
En la situación de equilibrio
Las fuerzas sobre la partícula de masa m2 son
En la situación de equilibrio
Eliminando la tensión T
Llamamos μs=tanλ
Nos queda un sistema de dos ecuaciones
Eliminamos m1
Simplificamos el primer miembro
Simplificamos el segundo miembro, empleando las relaciones trigonométricas
El resultado es
Finalmente, despejamos la masa añadida, Δm1
Referencias
Indian National Physics Olympiad. Homi Bhabha Centre for Science Eduaction. Solved papers NSEP & INPhO, 2016-2018. Ejemplo 45, pp. 46

