Medida del coeficiente cinético (II).
Primer procedimiento
La aceleración del bloque que desliza a lo largo del plano inlinado de ángulo θ es
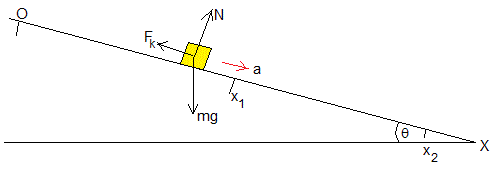
Marcamos en el plano inclinado tres posiciones equidistantes, x=0 (de partida), x1=Δx (intermedio) y x2=2Δx (de llegada)
El móvil parte de la posición x=0 con velocidad v0
Restamos la segunda de la primera
En el sistema de dos ecuaciones
Eliminamos la velocidad inicial v0 desconocida
Obtenemos la ecuación de una recta y=ax+b
El coeficiente cinético μk se obtiene
Resultados
El programa interactivo, más abajo, nos permite obtener una tabla de valores, de los tiempos t1 y t2 en función del ángulo del plano inclinado θ (en grados)
| θ | 20 | 22 | 24 | 26 | 28 | 30 | |
|---|---|---|---|---|---|---|---|
| t1 | 0.731 | 0.790 | 0.786 | 0.523 | 0.676 | 0.574 | |
| t2 | 1.294 | 1.262 | 1.186 | 0.847 | 0.988 | 0.856 |
t1=[0.731, 0.790, 0.786,0.523,0.676,0.574];
t2=[1.294,1.262, 1.186,0.847,0.988,0.856];
th=(20:2:30)*pi/180;
x=cot(th);
y=(1./(t2-t1)-1./t1)./(t2.*sin(th));
plot(x,y,'ro','markersize',3,'markerfacecolor','r')
grid on
xlabel('x')
ylabel('y')
title('Coeficiente cinético')
En el menú seleccionamos Tools/Basic Fitting. Aparece el cuadro de diálogo
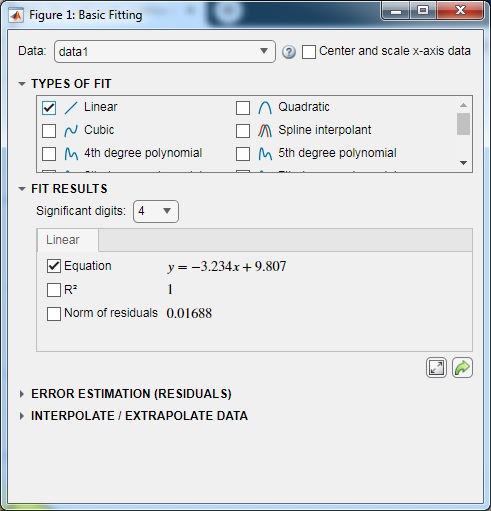
Activamos la casilla Linear. Aparece la figura
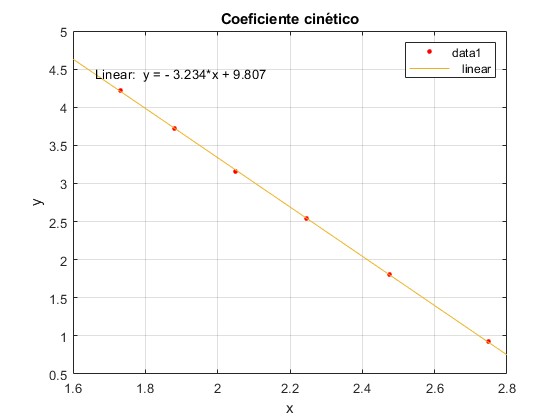
El coeficiente cinético es μk=-a/b=3.234/9.807=0.3298
El propósito de esta práctica ideal es de servir de modelo a una práctica real. La ventaja es que el coeficiente cinético μk es idependiente de la velocidad inicial v0 del cuerpo que desliza y del desplazamiento Δx
Actividades
El programa interactivo genera de forma aleatoria el valor del coeficiente cinético
Se establece el ángulo del plano inclinado, en el control titulado Angulo
A continuación, se pulsa el botón Nuevo generándose una velocidad inicial v0 aleatoria. A continuación, se pulsa ►. Si el bloque no llega al segundo interruptor, incrementamos el ángulo y volvemos a pulsar el botón Nuevo y así, sucesivamente.
Procedimiento de aproximaciones sucesivas para la medida del ángulo crítico
Como vemos en la figura, las fuerzas que actúan sobre el bloque son, el peso mg, la reacción del plano inclinado N y la fuerza de rozamiento, opuesta al movimiento.
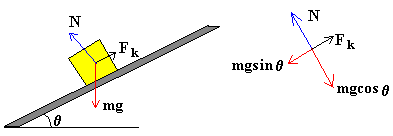
Como hay equilibrio en sentido perpendicular al plano inclinado, la fuerza normal N es igual a la componente perpendicular al plano inclinado del peso.
N=mg cos θ
Si el bloque se mueve con velocidad constante (aceleración cero) la componente del peso a lo largo del plano inclinado es igual a la fuerza de rozamiento.
mg sinθ =Fr
Como el bloque se está moviendo la fuerza de rozamiento es igual al producto del coeficiente de rozamiento cinético por la fuerza normal.
Fr=μkN
Con estas ecuaciones obtenemos que la medida del coeficiente de rozamiento por deslizamiento que viene dado por la tangente del ángulo que forma el plano inclinado con la horizontal. A este ángulo para el cual el movimiento del bloque es uniforme, le denominaremos ángulo crítico.
μk= tan θ
Podríamos medir el coeficiente de rozamiento estático mediante este experimento, a partir del ángulo para el cual el bloque comienza a deslizar. Se cumple entonces que la tangente del ángulo crítico (el ángulo del plano para el cual el bloque va a empezar a deslizar) es igual al coeficiente de rozamiento estático μs=tan θ
Para determinar cuando un movimiento es uniforme situamos tres detectores a lo largo del plano inclinado. Cuando el bloque pasa por el primer detector (se abre simulando un pequeño interruptor o una célula fotoeléctrica), pone el marcha el primer cronómetro. Cuando el bloque pasa por el segundo detector para el primer cronómetro y pone en marcha el segundo cronómetro. Cuando el bloque pasa por el tercer detector para el segundo cronómetro.
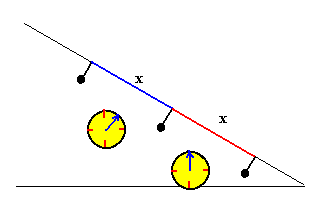
Si el detector central es equidistante de los extremos, se pueden producir los siguientes casos:
- Si el bloque acelera, el tiempo medido por el primer cronómetro es mayor que el medido por el segundo cronómetro.
- Si el bloque decelera: el tiempo medido por el primer cronómetro es menor que el medido por el segundo.
- Si el bloque se mueve con velocidad constante: los tiempos medidos por ambos cronómetros son aproximadamente iguales.
El gráfico situado en la parte derecha nos ayuda a determinar el ángulo para el cual el bloque desliza con velocidad constante mediante aproximaciones sucesivas:
- En color rojo, se representa los ángulos para los cuales el bloque acelera.
- En color azul se representan los ángulos para los cuales el bloque sigue un movimiento decelerado.
Por ejemplo, si para el ángulo θ1 el movimiento es acelerado y para el ángulo θ2 el movimiento es decelerado, la solución buscada (el ángulo para el cual el bloque desliza con velocidad constante) se encontrará en el intervalo (θ1,θ2)
Disminuyendo este intervalo nos acercaremos cada vez más al valor del ángulo crítico buscado y por tanto, al valor del coeficiente cinético.
De este modo, para determinar si el movimiento del bloque desde el primer detector en adelante es uniforme, no nos interesan los valores de los tiempos medidos por los cronómetros, solamente, si el tiempo medido por el primero es mayor, menor o igual al tiempo medido por el segundo.
Actividades
El programa interactivo genera de forma aleatoria los valores de los coeficientes estático y cinético, siendo el primero ligeramente mayor que el segundo.
Se establece el ángulo del plano inclinado, en el control titulado Angulo
A continuación, se pulsa el botón Nuevo y a continuación ►. Si el bloque no se mueve, incrementamos el ángulo y volvemos a pulsar el botón Nuevo y así sucesivamente, hasta que el bloque empiece a deslizar.
La clave para realizar la experiencia simulada estriba en cambiar el ángulo del plano inclinado mientras el bloque desliza hasta el primer detector. Una vez que el bloque ha sobrepasado el primer detector, no se puede cambiar el ángulo de inclinación.
Otra opción interesante, es la visualización de los vectores fuerza que actúan sobre el bloque, activando la casilla titulada Fuerzas. Cuando se incrementa el ángulo de inclinación, aumenta la componente del peso a lo largo del plano y también, lo hace la fuerza de rozamiento, mientras el bloque está en reposo. Cuando la fuerza de rozamiento alcanza el valor máximo, el bloque empieza a deslizar y la fuerza de rozamiento disminuye.
Referencias
Fathan Akbar, Nova Lailatul Rizkiyah, Mikrajuddin Abdullah. Minimal Tools for Accurately Measuring the Coefficient of Kinetic Friction.

