Medida del coeficiente cinético (I)
No hay rozamiento
Si suponemos que el plano inclinado de ángulo θ no presenta rozamiento μ=0
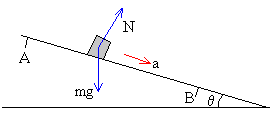
Las fuerzas sobre el cuerpo son:
-
El peso mg
-
La reacción del plano N
Como hay equilibrio en sentido perpendicular al plano inclinado
N=mgcosθ
Aplicando la segunda ley de Newton al movimiento a lo largo del plano
ma= mgsinθ
a= gsinθ
Si el cuerpo parte del reposo en la posición A, las ecuaciones del movimiento son:
Conocido el ángulo θ que forma el plano inclinado con la horizontal, el desplazamiento x del móvil entre A y B y el tiempo t que emplea en desplazarse, despejamos la aceleración de la gravedad g
Cuando hay rozamiento
Para que el cuerpo se mueva hacia abajo, la componente del peso mgsinθ tiene que ser mayor o igual que el máximo valor de la fuerza de rozamiento μsN=μsmgcosθ. El ángulo θ del plano inclinado deberá cumplir, tanθ≥μs
Supongamos que los coeficientes estático μs y cinético μk son iguales
- Movimiento hacia abajo
-
El peso mg
-
La reacción del plano N
-
La fuerza Fr de rozamiento que se opone al movimiento del cuerpo
- Movimiento hacia arriba
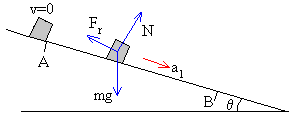
Las fuerzas sobre el cuerpo son:
Supondremos que el coeficiente de rozamiento μ es pequeño, de modo que se cumple siempre que tanθ>μ
Aplicamos la segunda ley de Newton al movimiento del cuerpo en la dirección del plano inclinado hacia abajo.
ma1=mgsinθ-Fr,
Fr=μN=μmgcosθ
La aceleración a1, vale
a1=g(sinθ-μcosθ)
Se mide el desplazamiento x1 del cuerpo, desde A hasta B y el tiempo t1 que emplea en desplazarse partiendo de A en reposo. A partir de estos dos datos, se obtiene la aceleración a1
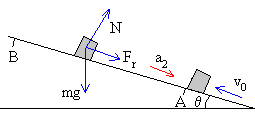
Aplicamos la segunda ley de Newton al movimiento del cuerpo en la dirección del plano inclinado hacia arriba.
ma2=mgsinθ+Fr,
Fr=μN=μmgcosθ
La aceleración a2, vale
a2=g(sinθ+μcosθ)
Se lanza el cuerpo en A con velocidad inicial v0, se mide el desplazamiento x2, desde A hasta que se para en B, y el tiempo t2 que emplea en desplazarse. A partir de estos dos datos, se obtiene la aceleración a2. Teniendo en cuenta, que la velocidad inicial v0 y la aceleración a2 son de signos contrarios.
Conocidas las aceleraciones a1 y a2 y el ángulo θ que forma el plano inclinado con la horizontal, se plantea un sistema de dos ecuaciones con dos incógnitas de las cuales se despeja g y μ.
a1=g(sinθ-μcosθ)
a2=g(sinθ+μcosθ)
Medida del coeficiente cinético de rozamiento y la aceleración de la gravedad
Una de las dificultades experimentales consiste en establecer con precisión la posición inicial y la velocidad inicial de un cuerpo. Se empieza a contar el tiempo cuando el cuerpo inicialmente en reposo en una determinada posición, se suelta. También es difícil medir con precisión la posición final del cuerpo, cuando su velocidad se hace cero, entonces se para el cronómetro.
Estas dificultades se evitan si disponemos a lo largo del plano inclinado de tres detectores que ponen en marcha y paran dos cronómetros.
-
Movimiento hacia abajo
-
Movimiento hacia arriba
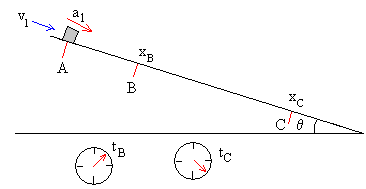
El cuerpo desciende a lo largo del plano inclinado con aceleración a1 y llega a A con una velocidad v1 desconocida. Tomando A como posición inicial, mediante detectores se mide el tiempo tB que tarda en llegar a B y el tiempo tC que tarda en llegar a la posición C. En este caso, la velocidad inicial y la aceleración son del mismo signo.
Eliminando v1 y despejando a1
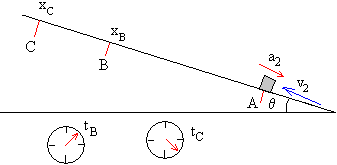
El cuerpo asciende a lo largo del plano inclinado con aceleración a2, y llega a A con velocidad v2 desconocida. Tomando A como posición de partida, mediante detectores se mide el tiempo tB que tarda en llegar a la posición B, y el tiempo tC que tarda llegar a C. En este caso, la velocidad inicial y la aceleración son de signos contrarios.
Eliminando v2 y despejando a2, obtenemos la misma expresión cambiada de signo
Una vez que hemos calculado a1 y a2 se determina el coeficiente cinético de rozamiento μ y la aceleración de la gravedad g mediante las fórmulas deducidas en el apartado anterior.
Ejemplo
Plano inclinado de ángulo θ=20º
-
Movimiento hacia abajo
-
Movimiento hacia arriba
xB=0.5
m, tB=0.72 s
xC=1.0
m, tC=1.19 s
xB=0.5
m, tB=0.16 s
xC=1.0
m, tC=0.44 s
Resultados
Actividades
-
Se establece el ángulo del plano inclinado θ, en el control titulado Angulo
-
Se activa el botón de radio titulado hacia abajo
Se pulsa el botón titulado Nuevo
Se observa el movimiento hacia abajo del cuerpo deslizando a lo largo del plano inclinado. Dos relojes situados en la parte inferior, miden el tiempo que tarda el cuerpo en desplazarse desde la posición del primer detector A a la del segundo B y desde la posición del primer detector A a la del tercero C.
-
Sin cambiar el ángulo del plano inclinado, se activa el botón de radio titulado hacia arriba
La regla cambia de sentido y la posición de los detectores se invierte, el primer detector A está ahora, en la parte inferior y el tercer detector C, en la parte superior
Se pulsa el botón titulado Nuevo
Se observa el movimiento hacia arriba del cuerpo deslizando a lo largo del plano inclinado.
Dos relojes situados en la parte inferior, miden el tiempo que tarda el cuerpo en desplazarse desde la posición del primer detector A a la del segundo B y desde la posición del primer detector A a la del tercero C.
Activando la casilla Fuerzas, observamos las fuerzas sobre el cuerpo, cuando asciende a lo largo del plano inclinado y cuando desciende.
Referencias
Venable D. D., Batra A.P., Hubsch T., Modifying the inclined-plane experiment. The Physics Teacher, 39, April 2001, pp. 215-217

