Consideremos dos bloques A y B unidos por una cuerda inextensible que pasa por una polea de masa despreciable. Cuando el bloque A desciende una altura h es detenido por una placa y la cuerda deja de tirar del bloque B. El bloque B desliza a lo largo del plano horizontal hasta que se detiene después de desplazarse una distancia x.

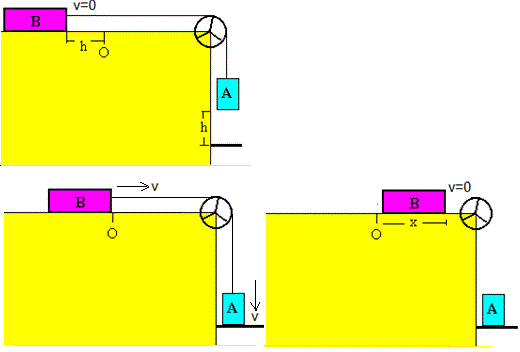
En la figura se muestra: en la parte de arriba, la situación inicial. En la de abajo, la situación intermedia, cuando el bloque A es detenido por la placa y la situación final, cuando el bloque B se detiene. El problema tiene dos partes:

• Movimiento del sistema formado por los dos bloques unidos por una cuerda
• Movimiento del bloque B sobre el plano horizontal, cuando el bloque A se ha detenido

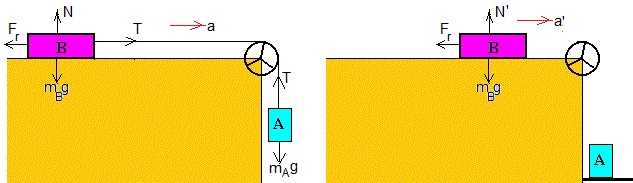
Los cuerpos parten del reposo, alcanzan su velocidad máxima cuando el cuerpo A se detiene después de descender una altura h, a continuación, el bloque B decelera hasta que se detiene después de recooreer una distancia x

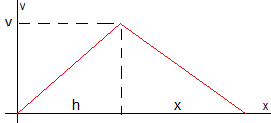
Movimiento del sistema formado por los dos bloques unidos por una cuerda

En la figura, se representan las fuerzas sobre cada unos de los bloques (en color azul) y la aceleración (en color rojo).

Sobre el cuerpo A de masa m_A actúan dos fuerzas

• El peso m_Ag
• La tensión de la cuerda T.

Sobre el bloque B actúan cuatro fuerzas

• El peso m_Bg
• La tensión de la cuerda T.
• La reacción del plano horizontal N=m_Bg
• La fuerza de rozamiento F_r=μ_k·N

• La ecuación del movimiento del bloque A es

m_A·g-T=m_A·a

• La ecuación del movimiento del bloque B es

T -F_r=m_B·a

Despejando la aceleración a en el sistema de dos ecuaciones

${\displaystyle a=\frac{m_A-{\mu }_k{m}_B}{m_A+m_B}g}$

La velocidad que alcanza después de desplazarse h, partiendo del reposo es

${\displaystyle v^2=2\frac{m_A-{\mu }_k{m}_B}{m_A+m_B}gh}$

Movimiento del bloque B sobre el plano horizontal

La cuerda deja de tirar del bloque B cuando pasa por la posición señalada por O.

El bloque B se detiene después de desplazarse x.

 Las fuerzas que actúan sobre el bloque B son 

• El peso m_B·g
• La reacción del plano horizontal N=m_B·g
• La fuerza de rozamiento F_r=μ_k·N

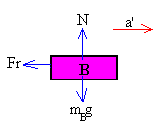
La ecuación del movimiento es

F_r=m_B·a’

a’= -μ_kg

De las ecuaciones del movimiento rectilíneo uniformemente acelerado, tenemos

${\displaystyle \begin{array}{l}0=v-{\mu }_{k}g·t\\ x=vt-\frac{1}{2}{\mu }_{k}g·t^2\end{array}}$

Eliminando el tiempo t

${\displaystyle x=\frac{1}{2}\frac{v^2}{{\mu }_{k}g}=\frac{m_A-{\mu }_k{m}_B}{m_A+m_B}\frac{h}{{\mu }_k}}$

Conocidos x y h y los valores de las masas m_A y m_B se puede determinar el coeficiente cinético μ_k.

${\displaystyle {\mu }_k=\frac{m_{A}h}{(m_A+m_B)x+m_{B}h}}$

Cuando las masas son iguales m_A=m_B para determinar el coeficiente μ_k solamente es necesario medir las distancias h y x.

${\displaystyle {\mu }_k=\frac{h}{h+2x}}$

Ejemplo

• Masa del bloque B, m_B=2.5 kg.
• Masa del bloque A, m_A=6.3 kg.
• El desplazamiento h=1.0 m
• El desplazamiento del bloque B después de dejar de actuar la cuerda es x=0.75 m

${\displaystyle {\mu }_k=\frac{m_{A}h}{(m_A+m_B)x+m_{B}h}=\frac{6.3·1.0}{(6.3+2.5)·0.75+2.5·1.0}=0.692}$

Comprobación:

Calculamos la aceleración del sistema formado por el bloque A y el bloque B unidos por una cuerda

${\displaystyle a=\frac{m_A-{\mu }_k{m}_B}{m_A+m_B}g=\frac{6.3-0.692·2.5}{6.3+2.5}9.8=5.09{\text{m/s}}^{\text{2}}}$

La velocidad del bloque B cuando pasa por O, en el instante en el que deja de actuar la cuerda es v=3.19 m/s empleando un tiempo de t=0.63 s.

Tenemos ahora, un bloque con velocidad inicial de v=3.19 m/s que desliza a lo largo de un plano horizontal con rozamiento, es decir, con una aceleración a’= -μ_kg=-0.692·9.8=-6.78 m/s² de sentido contrario a la velocidad.

El tiempo que tarda en parase es t=0.47 s, y se desplaza x=0.75 m

El desplazamiento total del bloque B es de 1.75 m y el tiempo que tarda en desplazarse es de 0.63+0.47=1.10 s.

Balance energético

Nos fijamos en el primer dibujo de esta página. En la primera etapa del movimiento, la energía potencial del bloque A, m_Agh se convierte en energía cinética de los dos bloques A y B. Mientras el bloque B se desplaza h por el plano horizontal, la fuerza de rozamiento realiza un trabajo -F_rh. El balance energético se escribe

${\displaystyle -{\mu }_k{m}_{B}gh=\frac{1}{2}\left(m_A+m_B\right)v^2-m_{A}gh}$

En la segunda etapa del movimiento, el bloque B que llevaba una velocidad v cuando pasa por O, se desplaza x hasta que se detiene. La energía cinética del bloque B se transforma en trabajo de la fuerza de rozamiento

${\displaystyle -{\mu }_k{m}_{B}gx=0-\frac{1}{2}{m}_B{v}^2}$

Eliminamos la velocidad v para despejat el coeficiente cinético μ_k

${\displaystyle {\mu }_k=\frac{m_{A}h}{\left(m_A+m_B\right)x+m_{B}h}}$

Actividades

Se introduce

• La masa del bloque A, en el control titulado Masa A

• La masa del bloque B está fijada en el programa interactivo en 2.5 kg

• El desplazamiento h inicial del bloque B, mientras acelera, en 1 m

Se pulsa el botón Nuevo.

Se mide el desplazamiento x del bloque a partir del origen O, es decir, a partir del momento en el que deja de actuar la cuerda. Se calcula el coeficiente cinético.

Activando la casilla titulada Fuerzas se representan las fuerzas que actúan sobre el bloque B.

Práctica de laboratorio

El laboratorio dispone de un carril de aluminio, sobre el carril se pone un carrito de 261 g de masa al que se le acopla un dispositivo que puede incrementar o reducir el rozamiento cuando se mueve sobre el carril. Sobre el carrito colocamos una pesa de 250 g por lo que su masa es m=0.511 kg

Para mover el carrito, lo atamos mediante una cuerda que pasa por una polea y en su extremo ponemos un contrapeso de masa M=0.015 kg. El carrito es acelerado mientras la pesa M cae una distancia h. La pesa se detiene y el carrito decelera hasta que se para recorriendo una distancia x

El sensor de movimiento recoge la posición del carrito en función del tiempo. El programa CAPSTONE calcula y representa la velocidad del carrito en función de su posición. Con la herrmamienta Coordenadas, medimos la máxima velocidad v y con la herramienta Delta medimos la distancia h desde que parte hasta que alcanza la velocidad máxima y la distancia x desde esta posición hasta que se detiene. Con estos datos calculamos el coeficiente cinético μ_k

${\displaystyle {\mu }_k=\frac{m_{A}h}{(m_A+m_B)x+m_{B}h}}$

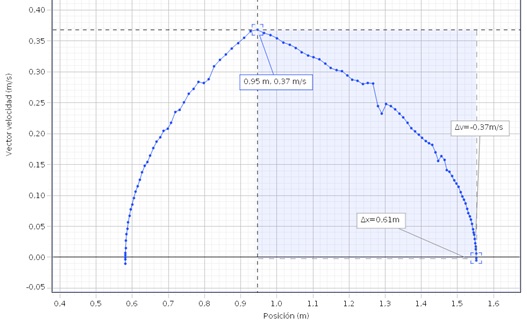
Los resultados son los siguientes:

Medida del coeficiente cinético con una balanza electrónica

Se coloca un cuerpo de masa m_A sobre una pista horizontal. Un papel grueso (en color rojo) se inserta entre el bloque y la pista. El cuerpo A se une mediante una cuerda inextensible y de masa despreciable que pasa por una polea ideal (sin masa y rozamiento) a otro cuerpo B de masa m_B que descansa sobre una balanza electrónica.

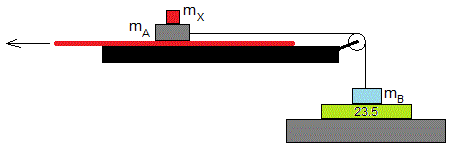
Se colocan pesas de masa m_X sobre el cuerpo A y se tira lentamente a velocidad constante del papel paralelamente a la pista. Se apunta la medida m_Y de la balanza electrónica.

En la figura, se muestran las fuerzas sobre el cuerpo A y sobre el cuerpo B

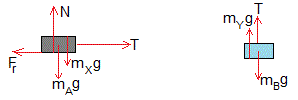
• Equilibrio del cuerpo A

${\displaystyle \begin{array}{l}\{\begin{array}{l}N=m_{A}g+m_{X}g\\ T=F_r={\mu }_{k}N\end{array}\\ T={\mu }_k\left(m_A+m_X\right)g\end{array}}$

• Equilibrio del cuerpo B

${\displaystyle T=m_{B}g-m_{Y}g}$

Donde m_Yg es la fuerza que ejerce la balanza electrónica sobre el cuerpo B

Eliminando la tensión T de la cuerda

${\displaystyle \begin{array}{l}{\mu }_k\left(m_A+m_X\right)g=m_{B}g-m_{Y}g\\ m_Y=-{\mu }_k{m}_X+\left(m_B-{\mu }_k{m}_A\right)\end{array}}$

Que es la ecuación de una recta de pendiente -μ_k

Cambiamos la masa m_X sobre el cuerpo A añadiendo más pesas y repetimos la medida

Realizamos una experiencia y recogemos los datos que figuran en la tabla.

mX=(0:20:120);
mY=[86.58,82.52,77.92,73.81,68.52,63.44,57.81];
plot(mX,mY,'ro','markersize',3,'markerfacecolor','r')
grid on
xlabel('m_X (g)')
ylabel('m_Y (g)')
title('Medida del coeficiente cinético')

Elegimos en el el menú Tools la opción Basic Fitting, en el cuadro de diálogo que aparece, activamos la casilla Linear dentro de la opción TYPES OF FIT

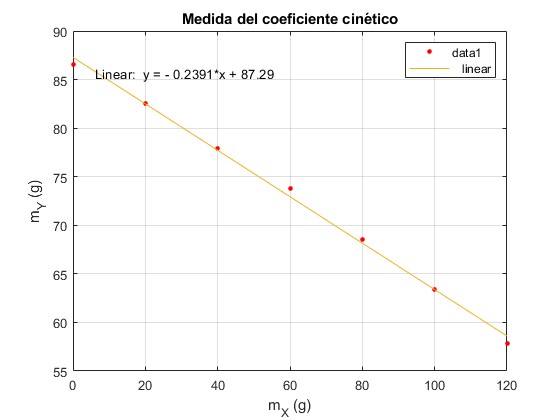
La pendiente de la recta de ajuste cambiada de signo, es el coeficiente cinético μ_k=0.24

Referencias

Eagleson H. V., An experimental method for determining coefficients of sliding friction. Am. J. Phys. 13 (1945), pp. 43-44

Reidl C. The coefficient of kinetic friction. The Physics Teacher. September 1990, pp. 40

Duan-bin Luo. Using an electronic balance to measure the kinetic friction coefficient in class experiment. Phys. Educ. 60 (2025) 015013