Circuitos de corriente alterna

Circuito en serie LCR

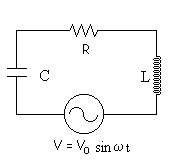
La impedancia es

$Z = Z_{R} + Z_{C} + Z_{L} = R + i (ω L - \frac{1}{ω C}) {\begin{cases} | Z | = \sqrt{R^{2} + {(ω L - \frac{1}{ω C})}^{2}} \\ \tan φ = \frac{ω L - \frac{1}{ω C}}{R} \end{cases}$

En el circuito de la figura, V=230·sin(2π·50)

La resistencia vale R=100Ω, la capacidad C=10 μF y la bobina L=0.1 H

$\begin{array}{l} | Z | = \sqrt{100^{2} + {(2 π \cdot 50 \cdot 0.1 - \frac{1}{2 π \cdot 50 \cdot 10 \cdot 10^{- 6}})}^{2}} = 104.82 Ω \\ \tan φ = \frac{2 π \cdot 50 \cdot 0.1 - \frac{1}{2 π \cdot 50 \cdot 10 \cdot 10^{- 6}}}{100} φ = - 1.23 \\ i = 0.76 \cdot \sin (2 π \cdot 50 t - 1.23) \end{array}$

>> w=2*pi*50;
>> ZR=100;
>> ZC=-i/(w*10e-6);
>> ZL=i*w*0.1;
>> Z=ZR+ZC+ZL;
>> abs(Z)
ans =  303.8226
>> phi=angle(Z)
phi =   -1.2354
>> I0=230/abs(Z)
I0 =    0.7570

Circuito en paralelo

Con los mismos datos del ejercico anterior resolvemos el siguiente circuito

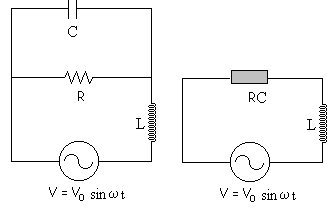
El condensador y la resistencia están en paralelo

$\begin{array}{l} \frac{1}{Z_{R C}} = \frac{1}{Z_{R}} + \frac{1}{Z_{C}} \frac{1}{Z_{R C}} = \frac{1}{100} + \frac{1}{- i / (2 π \cdot 50 \cdot 10 \cdot 10^{- 6})} \\ Z = Z_{L} + Z_{R C} = 2 π \cdot 50 \cdot 0.1 i + (91.02 - 28.59 i) = 91.02 + 2.82 i {\begin{cases} | Z | = 91.06 \\ φ = 0.03 \end{cases} \\ i = 2.53 \sin (2 π \cdot 50 t + 0.03) \end{array}$

>> w=2*pi*50;
>> ZR=100;
>> ZC=-i/(w*10e-6);
>> ZL=i*w*0.1;
>> ZRC=1/(1/ZR+1/ZC);
>> Z=ZL+ZRC
Z =  91.0170 + 2.8221i
>> abs(Z)
ans =   91.0607
>> phi=angle(Z)
phi =    0.0310
>> I0=230/abs(Z)
I0 =    2.5258

Otros circuitos de corriente alterna

Resolver el cuircuito de la figura

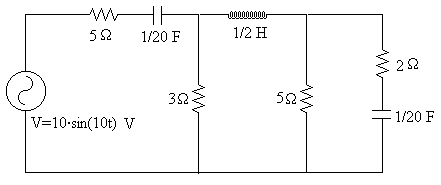
Sabiendo que ω=10 rad/s, las impedancias de los dos condensadores y de la autoinducción son

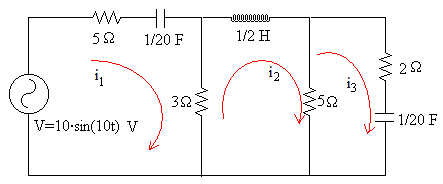
$\begin{array}{l} Z_{C} = - i \frac{1}{ω C} = - i \frac{1}{10 \cdot (1 / 20)} = - 2 i \\ Z_{L} = i ω L = i \cdot 10 \cdot (1 / 2) = 5 i \end{array}$

Las ecuaciones del circuito son

$\begin{array}{l} {\begin{cases} (8 - 2 i) i_{1} - 3 i_{2} = 10 \\ - 3 i_{1} + (8 + 5 i) i_{2} - 5 i_{3} = 0 \\ - 5 i_{2} + (7 - 2 i) i_{3} = 0 \end{cases} \\ (\begin{matrix} 8 - 2 i & - 3 & 0 \\ - 3 & 8 + 5 i & - 5 \\ 0 & - 5 & 7 - 2 i \end{matrix}) (\begin{matrix} i_{1} \\ i_{2} \\ i_{3} \end{matrix}) = (\begin{matrix} 10 \\ 0 \\ 0 \end{matrix}) \end{array}$

Z=[8-2i,-3,0;-3,8+5i,-5;0,-5,7-2i];
V=[10;0;0];
I=Z\V;
disp('intensidades (amplitudes)')
abs(I)
disp('fases en grados')
angle(I)*180/pi
%representación gráfica
col=['b' 'g' 'r'];
t=linspace(0,2*pi/10,100);
hold on
for k=1:3
    ic=abs(I(k))*sin(10*t+angle(I(k)));
    str=sprintf('i_%i\n',k);
    plot(t,ic,col(k),'displayName',str);
end
title('Circuito de corriente alterna')
xlabel('t')
ylabel('Intensidad')
legend('-DynamicLegend','location','NorthEast')
grid on
hold off

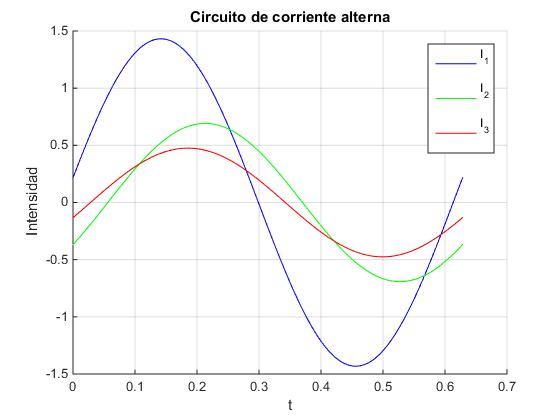
En la ventana de comandos obtenemos el módulo de cada una de sus intensidades y sus fases respectivas expresadas en grados.

intensidades (amplitudes)
ans =
    1.4322
    0.6922
    0.4754
fases en grados
ans =
    8.6689
  -32.1402
  -16.1948