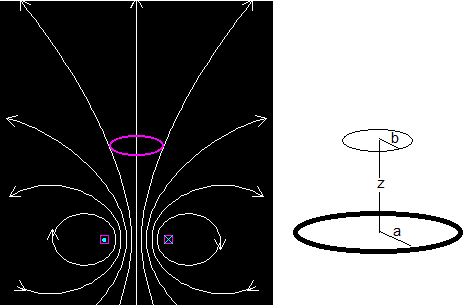
Consideremos dos circuitos acoplados formados por una bobina y una espira que tienen el mismo eje y están situadas en planos paralelos separados una distancia z. La bobina está formada por N espiras apretadas de radio a, y la espira tiene un radio b.

La bobina constituye el primario de nuestro circuito acoplado, por el que va a circular una corriente alterna de frecuencia angular ω y intensidad I₁.

I₁=I₀₁·sin(ω t).

Queremos calcular la intensidad I₂ que circulará por la espira (secundario) sabiendo que su resistencia es R.

Para calcular el coeficiente de inducción mutua M de dos circuitos acoplados, hemos de seguir los siguientes pasos:

1. Calculamos el campo magnético producido por el primario
2. Hallamos el flujo del campo magnético producido por el primario a través del secundario
3. Obtenemos la expresión del coeficiente de inducción mutua, dividiendo dicho flujo entre la intensidad que circula por el primario.

Campo magnético producido por el primario

El primer paso requiere aplicar la ley de Biot-Savart para determinar el campo magnético producido por una espira.

${\displaystyle \begin{array}{l}{B}_{\rho }=\frac{{\mu }_0}{2\pi }ia·z{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}\frac{\sin \phi }{{\left(\sqrt{a^2+z^2+{\rho }^2-2a\rho ·\sin \phi }\right)}^3}}d\phi \\ B_z=\frac{{\mu }_0}{2\pi }ia{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}\frac{a-\rho ·\sin \phi }{{\left(\sqrt{a^2+z^2+{\rho }^2-2a\rho ·\sin \phi }\right)}^3}}d\phi \end{array}}$

Flujo del campo magnético a través del secundario

Sea I₁ la corriente que circula por el primario. Calculamos el flujo del campo magnético producido por el primario a través del área encerrada por la espira de radio b (secundario).

${\displaystyle {\Phi }_2=\underset{S}{{\displaystyle \int }}\overrightarrow{B}\cdot \overrightarrow{dS}=\underset{S}{{\displaystyle \int }}(B_{\rho }\widehat{j}+B_z\widehat{k})\cdot dS·\widehat{k}=\underset{S}{{\displaystyle \int }}{B}_z·dS}$

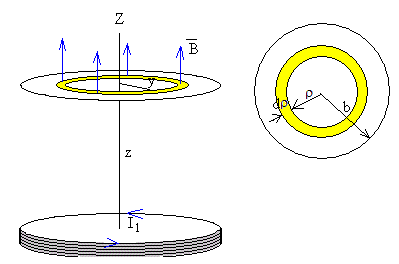
Dado que el plano de la espira es perpendicular al eje Z, el flujo de la componente Y del campo es nulo.

El elemento diferencial de área es el área de un anillo de radio ρ y de anchura dρ, su área es dS=2πρ·dρ

${\displaystyle {\Phi }_2={\mu }_{0}N·I_{1}a{\displaystyle \underset{0}{\overset{b}{\int }}\rho ·d\rho }{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}\frac{a-\rho ·\sin \phi }{{\left(\sqrt{a^2+z^2+{\rho }^2-2a\rho ·\sin \phi }\right)}^3}}d\phi }$

Coeficiente de inducción mutua

Se define coeficiente de inducción mutua M como el cociente entre el flujo que atraviesa el secundario Φ₂ entre la intensidad que circula por el primario I₁.

${\displaystyle M=\frac{{\Phi }_2}{I_1}={\mu }_{0}Na{\displaystyle \underset{0}{\overset{b}{\int }}\rho ·d\rho }{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}\frac{a-\rho ·\sin \phi }{{\left(\sqrt{a^2+z^2+{\rho }^2-2a\rho ·\sin \phi }\right)}^3}}d\phi }$

Si la espira está alejada de la bobina, dipolo magnético, obtenemos una expresión aproximada para M

${\displaystyle \begin{array}{l}r=\sqrt{{\rho }^2+z^2}>>a\\ {\Phi }_2={\displaystyle \underset{0}{\overset{b}{\int }}\frac{{\mu }_{0}N·I_1{a}^2}{4r^3}\left(\frac{3z^2}{r^2}-1\right)·2\pi \rho ·d\rho }·\\ {\Phi }_2=\frac{\pi {\mu }_{0}N·I_1{a}^2}{4}\left(3z^2{\displaystyle \underset{0}{\overset{b}{\int }}\frac{2\rho d\rho }{{\left(\sqrt{{\rho }^2+z^2}\right)}^5}-}{\displaystyle \underset{0}{\overset{b}{\int }}\frac{2\rho d\rho }{{\left(\sqrt{{\rho }^2+z^2}\right)}^3}}\right)\end{array}}$

La expresión del coeficiente de inducción mutua M es

${\displaystyle M=\frac{{\Phi }_2}{I_1}=\frac{\pi {\mu }_{0}N{a}^2{b}^2}{2{\left(\sqrt{b^2+z^2}\right)}^3}}$

Fórmula del coeficiente de inducción mutua

Hemos calculado calculado el coeficiente de inducción mutua entre dos circuitos a partir de su definición. Ahora emplearemos la fórmula alternativa.

${\displaystyle M=\frac{{\mu }_0}{4\pi }{\displaystyle ∯\frac{\overrightarrow{d{l}_1}·\overrightarrow{d{l}_2}}{r}}}$

donde $\overrightarrow{d{l}_1}$ es un elemento del primer circuito, $\overrightarrow{d{l}_2}$ es un elemento del segundo circuito y r es la distancia entre ambos elementos. (Véase Lorrain P., Corson D. R.. Campos y Ondas Electromagnéticas, Selecciones Científicas, págs 366-367).

Espiras cuadradas

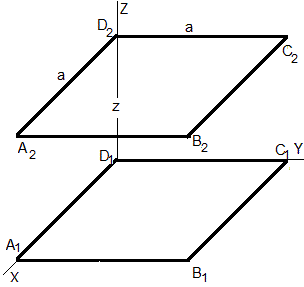
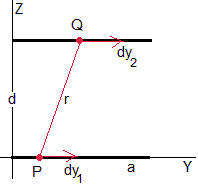
Consideremos dos espiras cuadradas de lado a, situadas en planos paralelos y distantes z, tal como se muestra en la figura.

La integral doble, es la suma de 16 términos, cada término es proporcional al producto escalar de dos vectores: A₁B₁ con A₂B₂, A₁B₁ con B₂C₂, A₁B₁ con C₂D₂, A₁B₁ con D₂A₂; B₁C₁ con A₂B₂, B₁C₁ con B₂C₂ y así, sucesivamente.

El producto escalar de dos vectores perpendiculares es cero, por ejemplo A₁B₁ con B₂C₂, por lo que la integral se reduce a ocho términos.

${\displaystyle \begin{array}{l}M=\frac{{\mu }_0}{4\pi }{\displaystyle ∯\frac{\overrightarrow{d{l}_1}·\overrightarrow{d{l}_2}}{r}}=\\ \frac{{\mu }_0}{4\pi }\left\{\begin{array}{l}{\displaystyle ∯\frac{d{x}_1\widehat{i}·d{x}_2\widehat{i}}{r_1}}+{\displaystyle ∯\frac{d{x}_1\widehat{i}·\left(-d{x}_2\widehat{i}\right)}{r_2}}+{\displaystyle ∯\frac{d{y}_1\widehat{j}·d{y}_2\widehat{j}}{r_1}}\\ +{\displaystyle ∯\frac{d{y}_1\widehat{j}·\left(-d{y}_2\widehat{j}\right)}{r_2}+{\displaystyle ∯\frac{\left(-d{x}_1\widehat{i}\right)·d{x}_2\widehat{i}}{r_2}}+{\displaystyle ∯\frac{\left(-d{x}_1\widehat{i}\right)·\left(-d{x}_2\widehat{i}\right)}{r_1}}}\\ +{\displaystyle ∯\frac{\left(-d{y}_1\widehat{j}\right)·d{y}_2\widehat{j}}{r_2}}+{\displaystyle ∯\frac{\left(-d{y}_1\widehat{j}\right)·\left(-d{y}_2\widehat{j}\right)}{r_1}}\end{array}\right\}=\\ \frac{{\mu }_0}{2\pi }\left\{{\displaystyle ∯\frac{d{x}_1·d{x}_2}{r_1}}-{\displaystyle ∯\frac{d{x}_1·d{x}_2}{r_2}}+{\displaystyle ∯\frac{d{y}_1·d{y}_2}{r_1}}-{\displaystyle ∯\frac{d{y}_1·d{y}_2}{r_2}}\right\}\end{array}}$

Para dos espiras cuadradas iguales, se reduce a dos términos

${\displaystyle \begin{array}{l}M=\frac{{\mu }_0}{\pi }\left\{{\displaystyle ∯\frac{d{y}_1·d{y}_2}{r_1}}-{\displaystyle ∯\frac{d{y}_1·d{y}_2}{r_2}}\right\}\\ r_1^2={\left(y_2-y_1\right)}^2+z^2\\ r_2^2=a^2+{\left(y_2-y_1\right)}^2+z^2\end{array}}$

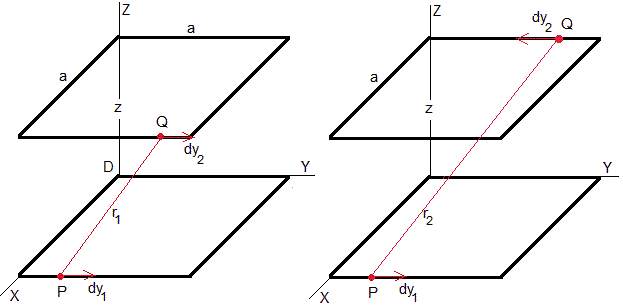
• r₁ es la distancia del punto P de coordenadas (a, y₁, 0) al punto Q (a, y₂, z). Figura de la izquierda

• r₂ es la distancia del punto P de coordenadas (a, y₁, 0) al punto Q (0, y₂, z). Figura de la derecha

Resolvemos la integral

${\displaystyle \begin{array}{l}{\displaystyle ∯\frac{d{y}_1·d{y}_2}{r}}\\ r^2={\left(y_2-y_1\right)}^2+d^2\{\begin{array}{l}{d}^2=z^2\\ d^2=z^2+a^2\end{array}\end{array}}$

o bien, la integral

${\displaystyle {\displaystyle \underset{0}{\overset{a}{\int }}d{y}_1{\displaystyle \underset{0}{\overset{a}{\int }}\frac{d{y}_2}{\sqrt{{\left(y_2-y_1\right)}^2+d^2}}}}}$

Teniendo en cuenta el resultado

${\displaystyle {\displaystyle \int \frac{dx}{\sqrt{x^2+d^2}}}=\ln \left(x+\sqrt{x^2+d^2}\right)}$

>> syms x d;
>> int(1/sqrt(x^2+d^2))
ans =log(x + (d^2 + x^2)^(1/2))

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{a}{\int }}\left\{{\ln \left(\left(y_2-y_1\right)+\sqrt{{\left(y_2-y_1\right)}^2+d^2}\right)|}_0^a\right\}d{y}_1}\\ {\displaystyle \underset{0}{\overset{a}{\int }}\left\{\ln \left(\left(a-y_1\right)+\sqrt{{\left(a-y_1\right)}^2+d^2}\right)-\ln \left(-y_1+\sqrt{y_1^2+d^2}\right)\right\}}d{y}_1\end{array}}$

Integrando por partes

${\displaystyle {\displaystyle \int \ln \left(x+\sqrt{x^2+d^2}\right)}dx=x\ln \left(x+\sqrt{x^2+d^2}\right)-\sqrt{x^2+d^2}}$

>> syms x d;
>>int(log(x+sqrt(x^2+d^2)))
ans =x*log(x + (d^2 + x^2)^(1/2)) - (d^2 + x^2)^(1/2)

Llegamos al siguiente resultado

${\displaystyle \begin{array}{l}{\left\{\begin{array}{l}-\left(a-y_1\right)\ln \left(\left(a-y_1\right)+\sqrt{{\left(a-y_1\right)}^2+d^2}\right)+\sqrt{{\left(a-y_1\right)}^2+d^2}\\ -y_1\ln \left(-y_1+\sqrt{y_1^2+d^2}\right)-\sqrt{y_1^2+d^2}\end{array}\right\}|}_0^a\\ \left\{d-a\ln \left(-a+\sqrt{a^2+d^2}\right)-\sqrt{a^2+d^2}-\left(-a\ln \left(a+\sqrt{a^2+d^2}\right)+\sqrt{a^2+d^2}-d\right)\right\}=\\ \left\{2d+a\ln \left(\frac{a+\sqrt{a^2+d^2}}{-a+\sqrt{a^2+d^2}}\right)-2\sqrt{a^2+d^2}\right\}=\\ 2\left\{d+a\ln \left(\frac{a+\sqrt{a^2+d^2}}{d}\right)-\sqrt{a^2+d^2}\right\}\end{array}}$

Nos queda evaluar las dos integrales dobles que son similares. En la primera integral, d=z, en la segunda integral, $d^2=z^2+a^2$

${\displaystyle \begin{array}{l}{\displaystyle ∯\frac{d{y}_1·d{y}_2}{r_1}}=2\left\{z+a\ln \left(\frac{a+\sqrt{a^2+z^2}}{z}\right)-\sqrt{a^2+z^2}\right\}\\ {\displaystyle ∯\frac{d{y}_1·d{y}_2}{r_2}}=2\left\{\sqrt{z^2+a^2}+a\ln \left(\frac{a+\sqrt{2a^2+z^2}}{\sqrt{z^2+a^2}}\right)-\sqrt{2a^2+z^2}\right\}\end{array}}$

Finalmente, el coeficiente de inducción mutua M es proporcional a la diferencia de estos dos resultados

${\displaystyle M=\frac{2{\mu }_0}{\pi }\left\{z+a\ln \left(\frac{a+\sqrt{a^2+z^2}}{z}\right)-a\ln \left(\frac{a+\sqrt{2a^2+z^2}}{\sqrt{a^2+z^2}}\right)-2\sqrt{a^2+z^2}+\sqrt{2a^2+z^2}\right\}}$

Espiras circulares

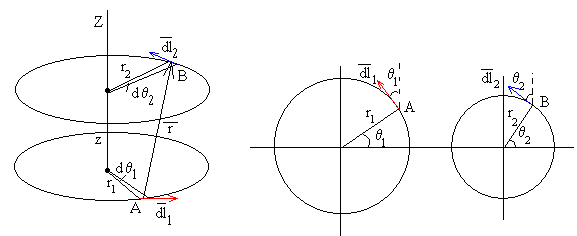
Como vemos en la figura, el elemento de corriente es un arco infinitesimal de circunferencia (arco igual a radio por ángulo comprendido) dl₁= r₁·dθ₁ y dl₂= r₂·dθ₂

${\displaystyle \begin{array}{l}\overrightarrow{d{l}_1}=r_{1}d{\theta }_1(-\sin {\theta }_1·\widehat{i}+\cos {\theta }_1·\widehat{j})\\ \overrightarrow{d{l}_2}=r_{2}d{\theta }_2(-\sin {\theta }_2·\widehat{i}+\cos {\theta }_2·\widehat{j})\end{array}}$

El vector $\overrightarrow{r}$ que tiene por origen el punto A (r₁·cosθ₁, r₁·sinθ₁, 0) y extremo el punto B (r₂·cosθ₂, r₂·sinθ₂, z), 

${\displaystyle \overrightarrow{r}=(r_2\cos {\theta }_2-r_1\cos {\theta }_1)\widehat{i}+(r_2\sin {\theta }_2-r_1\sin {\theta }_1)\widehat{j}+z\widehat{k}}$

Su módulo, o la distancia r entre dichos elementos de corriente es

${\displaystyle r=\sqrt{{\left(r_2\cos {\theta }_2-r_1\cos {\theta }_1\right)}^2+{\left(r_2\sin {\theta }_2-r_1\sin {\theta }_1\right)}^2+z^2}}$

Tenemos que calcular la integral doble

${\displaystyle M=\frac{{\mu }_0}{4\pi }{r}_1{r}_2{\displaystyle \underset{0}{\overset{2\pi }{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{\cos ({\theta }_2-{\theta }_1)d{\theta }_{1}d{\theta }_2}{\sqrt{r_1^2+r_2^2-2r_1{r}_2\cos ({\theta }_2-{\theta }_1)+z^2}}}}}$

Si el circuito primario consta de N₁ espiras iguales apretadas, y el circuito secundario consta de una sola espira, el coeficiente de inducción mutua es

${\displaystyle M=\frac{{\mu }_0}{4\pi }{N}_1{r}_1{r}_2{\displaystyle \underset{0}{\overset{2\pi }{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{\cos ({\theta }_2-{\theta }_1)d{\theta }_{1}d{\theta }_2}{\sqrt{r_1^2+r_2^2-2r_1{r}_2\cos ({\theta }_2-{\theta }_1)+z^2}}}}}$

El coeficiente de inducción mutua entre dos espiras de radios a y b, coaxiales y distantes z,  se puede expresar en términos de las integrales elípticas completas de primera  K(m) y segunda especie E(m), mediante la fórmula que damos sin demostración.

${\displaystyle \begin{array}{l}M=\frac{1}{2}{\mu }_0\sqrt{{(a+b)}^2+z^2}\left((2-m)K(m)-2E(m)\right)\\ m=\frac{4ab}{{(a+b)}^2+z^2}\end{array}}$

Si en vez de espiras, son bobinas de espiras apretadas de N_a y N_b vueltas se multiplica el coeficiente de inducción mutua de dos espiras por el producto N_a·N_b.

a=0.5; %radio espira
b=0.5; %radio espira
z=0.3; %distancia entre espiras
m=4*a*b/((a+b)^2+z^2);
[K,E]=ellipke(m);
M=0.5*sqrt((a+b)^2+z^2)*((2-m)*K-2*E)

>>format long
M =   0.369893700194511

El coeficiente de inducción mutua M hay que multiplicarlo por μ₀=4π·10^-7 para expresarlo en H (henrios)

Ley de Faraday

La corriente alterna que circula por el solenoide produce un campo magnético que varía con el tiempo. El flujo Φ₂ de dicho campo a través del anillo es

Φ₂=M·I₁

donde M es el coeficiente de inducción mutua del sistema formado por el solenoide y el anillo, I₁ es de la intensidad de la corriente en el solenoide que varía con el tiempo de la forma

I₁=I₀₁·sin(ω t)

Donde I₀₁ es la amplitud y ω frecuencia angular ω =2π f. En Europa f=50 Hz y en Estados Unidos f=60 Hz.

Aplicando la ley de Faraday, se obtiene la fem inducida V_ε en el anillo como resultado del cambio del flujo que lo atraviesa con el tiempo. Aplicando la ley de Lenz, se determina el sentido de la corriente inducida.

${\displaystyle V_2=-\frac{d{\Phi }_2}{dt}=-\frac{d(M·I_1)}{dt}=-M·I_{01}\omega \cos (\omega t)}$

La corriente inducida I₂ en la espira de resistencia R es

${\displaystyle I_2=\frac{V_2}{R}=-\frac{M}{R}{I}_{01}\omega \cos (\omega t)}$

Actividades

En la simulación tenemos dos circuitos acoplados

• El circuito primario es una bobina formada por N=100 espiras de radio a=3.5 cm de radio
• El circuito secundario es una espira de radio b que está situada a una altura z sobre la bobina.

Se introducen los siguientes datos relativos a la corriente que circula por el primario.

• La frecuencia f=50 Hz se ha fijado en el programa interactivo
• La amplitud de la intensidad I₀₁ en amperios en el control titulado Intensidad.
• La resistencia de la espira se obtiene aplicando la fórmula

${\displaystyle R=\rho \frac{l}{S}}$

Para una espira de radio b, hecha de un cable de aluminio de resistividad ρ =2.8·10^-8 Ω ·m cuya sección es de 5 mm de radio 

R=2.24·10^-3b Ω .

La resistencia se ha elegido, de modo que la intensidad de la corriente en la espira (secundario) sea del mismo orden de magnitud que la corriente en la bobina (primario).

A continuación, los datos relativos a la espira (secundario)

• Su radio b en cm en el control titulado Radio.
• La distancia z en cm entre los planos de la espira y de la bobina en el control titulado Posición

Se pulsa el botón titulado Nuevo.

• Vemos la corriente en la bobina (primario) representada por el movimiento de puntos de color rojo.
• La corriente inducida en la espira (secundario) representada por el movimiento de puntos de color rojo.

Se representa las componentes del campo magnético B_y y B_z en los siguientes puntos (0, z), (b/2, z) y (-b/2, z), mediante flechas de color azul.

Se representa la corriente en la bobina (primario) y la corriente inducida en la espira (secundario) en función del tiempo en la parte derecha.

En la parte superior, se muestra el valor del coeficiente de inducción mutua M.

Ejemplo 1

Si el radio de la espira b=3.5 cm y la distancia z=5 cm el coeficiente de inducción mutua vale M=9.67·10^-7 H. La resistencia de la espira vale

R=2.24·10^-3·0.035=7.84·10^-5 Ω

Si por el primario circula una corriente de frecuencia f=50 Hz y la amplitud de la intensidad vale I₀₁=10 A. La intensidad inducida que circula por la espira (secundario) es

${\displaystyle I_2=-\frac{9.67·{10}^{-7}}{7.84·{10}^{-5}}2\pi ·50·10·\cos (2\pi ·50·t)}$

La amplitud de la intensidad inducida es I₀₂=38.7 A

Ejemplo 2:

La espira tiene un radio b pequeño y está alejada de la bobina

Por ejemplo b=1 cm y z=10 cm.

Calculamos el coeficiente de inducción mutua por la fórmula aproximada

${\displaystyle M=\frac{\pi {\mu }_{0}N{a}^2{b}^2}{2{\left(\sqrt{b^2+z^2}\right)}^3}=\frac{\pi ·4·\pi ·{10}^{-7}·100·{(0.035)}^2·{(0.01)}^2}{2{\left(\sqrt{{0.01}^2+{.035}^2}\right)}^3}=2.38·{10}^{-8}\text{H}}$

Mediante cálculo numérico, empleando integrales elípticas, el valor que obtenemos es de 2.01·10^-8 H

La resistencia de la espira es

R=2.24·10^-3·0.01=2.24·10^-5 Ω

Si por el primario circula una corriente de frecuencia f=50 Hz y la amplitud de la intensidad vale I₀₁=10 A.

La intensidad inducida que circula por la espira (secundario) es

${\displaystyle I_2=-\frac{2.01·{10}^{-8}}{2.24·{10}^{-5}}2\pi ·50·10·\cos (2\pi ·50·t)}$

La amplitud de la intensidad inducida es I₀₂=2.82 A