En esta apartado, vamos a proporcionar una descripción más detallada del funcionamiento del transformador

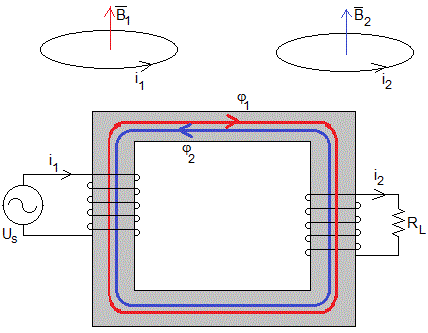
En la figura, se muestra un transformador con N₁ espiras en el primario y N₂ en el secundario. φ₁ es el flujo a través de una espira producido por la corriente i₁ en el primario y φ₂ es el flujo a través de una espira producido por la corriente i₂ en el secundario.

Secundario

El flujo a través de una espira del secundario es la diferencia φ=φ₂-φ₁. El flujo total en el secundario es

${\displaystyle N_2\phi =N_2{\phi }_2-N_2{\phi }_1}$

El coeficiente de inducción mutua M es el cociente entre el flujo a través del secundario (producido por el primario) y la corriente en el primario. El coeficiente de autoinducción L₂ es el cociente del flujo propio a través de un circuito de la derecha y la intensidad que circula por el mismo

${\displaystyle \begin{array}{l}M=\frac{N_2{\phi }_1}{i_1},L_2=\frac{N_2{\phi }_2}{i_2}\\ N_2\phi =L_2{i}_2-M{i}_1\end{array}}$

Derivando con respecto del tiempo

${\displaystyle N_2\frac{d\phi }{dt}=L_2\frac{d{i}_2}{dt}-M\frac{d{i}_1}{dt}}$

Aplicamos la ley de Faraday al secundario

${\displaystyle -N_2\frac{d\phi }{dt}={\displaystyle \underset{A}{\overset{B}{\int }}\overrightarrow{E_i}}·\overrightarrow{dl}=N_2{\displaystyle \oint \overrightarrow{E_i}·\overrightarrow{dl}=i_2\left(R_2+R_L\right)}}$

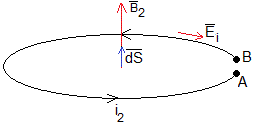
R₂ es la resistencia del secundario y R_L es la resistencia de un circuito externo (dispositivo) conectado a los extremos A y B del secundario

La ecuación del secundario es

${\displaystyle \begin{array}{l}-i_2\left(R_2+R_L\right)=L_2\frac{d{i}_2}{dt}-M\frac{d{i}_1}{dt}\\ M\frac{d{i}_1}{dt}=L_2\frac{d{i}_2}{dt}+i_2\left(R_2+R_L\right)\end{array}}$

Primario

Repetimos los pasos para obtener la ecuación del primario, intercambiando los papeles de primario y secundario

El flujo a través de una espira del primario es la diferencia φ=φ₁-φ₂. El flujo total en el primario es

${\displaystyle N_1\phi =N_1{\phi }_1-N_1{\phi }_2}$

El coeficiente de inducción mutua y de autoinducción son

${\displaystyle \begin{array}{l}M=\frac{N_1{\phi }_2}{i_2},L_1=\frac{N_1{\phi }_1}{i_1}\\ N_1\phi =L_1{i}_1-M{i}_2\end{array}}$

Derivando con respecto del tiempo

${\displaystyle N_1\frac{d\phi }{dt}=L_1\frac{d{i}_1}{dt}-M\frac{d{i}_2}{dt}}$

Aplicamos la ley de Faraday y la ley de Ohm al primario (véase el apartado titulado 'Ecuación del circuito RL'

${\displaystyle \begin{array}{l}\overrightarrow{E}=\overrightarrow{E_s}+\overrightarrow{E_i}\\ {\displaystyle \underset{A}{\overset{B}{\int }}\overrightarrow{E}·\overrightarrow{dl}}={\displaystyle \underset{A}{\overset{B}{\int }}\overrightarrow{E_s}·\overrightarrow{dl}}+{\displaystyle \underset{A}{\overset{B}{\int }}\overrightarrow{E_i}·\overrightarrow{dl}}\end{array}}$

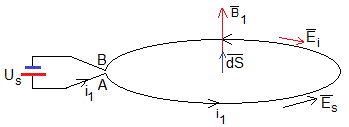
• El campo eléctrico total, $\overrightarrow{E}$ mueve las cargas en el conductor produciendo una intensidad i₁. La primera integral es el producto de la intensidad por la resistencia, i₁R₁.

• $\overrightarrow{E_s}$ es el campo eléctrico producido por la diferencia de potencial U_s de la batería, la segunda integral, es U_s

• Para N₁ espiras

${\displaystyle -N_1\frac{d\phi }{dt}={\displaystyle \underset{A}{\overset{B}{\int }}\overrightarrow{E_i}}·\overrightarrow{dl}=N_1{\displaystyle \oint \overrightarrow{E_i}·\overrightarrow{dl}}}$

El resultado es

${\displaystyle i_1{R}_1=U_s-N_1\frac{d\phi }{dt}}$

Sustituyendo en la primera ecuación, el primer término

${\displaystyle \begin{array}{l}{N}_1\frac{d\phi }{dt}=U_s-i_1{R}_1\\ L_1\frac{d{i}_1}{dt}-M\frac{d{i}_2}{dt}=U_s-i_1{R}_1\\ U_s=i_1{R}_1+L_1\frac{d{i}_1}{dt}-M\frac{d{i}_2}{dt}\end{array}}$

El comportamiento del transformador está descrito por dos ecuaciones, una para el circuito primario y otra, para el secundario

${\displaystyle \{\begin{array}{l}{i}_1{R}_1+L_1\frac{d{i}_1}{dt}-M\frac{d{i}_2}{dt}=U_s\\ i_2\left(R_2+R_L\right)+L_2\frac{d{i}_2}{dt}-M\frac{d{i}_1}{dt}=0\end{array}}$

Gráficas

Los datos del transformador son los siguientes:

• Primario: autoinducción L₁=3.69 H, resistencia, R₁=4.5 Ω, número de espiras N₁=900
• Secundario: autoinducción L₂=0.41 H, resistencia, R₂=1.4 Ω, número de espiras N₂=300
• El primario está conectado a una fem alterna de 60 Hz, ω=2π·60 rad/s, de amplitud U_s=50.2 V
• Coeficiente de inducción mutua, M=1.176 H

Las ecuaciones de los circuitos en forma compleja son

${\displaystyle \begin{array}{l}\{\begin{array}{l}{I}_1{R}_1+i\omega L_1{I}_1-i\omega M{I}_2=U_s\\ I_2\left(R_2+R_L\right)+i\omega L_2{I}_2-i\omega M{I}_1=0\end{array}\\ I_1=\frac{R_2+R_L+i\omega L_2}{\left(R_1+i\omega L_1\right)\left(R_2+R_L+i\omega L_2\right)+{\omega }^2{M}^2}{U}_s\\ I_2=\frac{i\omega M}{\left(R_1+i\omega L_1\right)\left(R_2+R_L+i\omega L_2\right)+{\omega }^2{M}^2}{U}_s\end{array}}$

I₁ e I₂ son números complejos que contienen la información acerca de la amplitud y la fase

L1=3.69; %primario
N1=900;
R1=4.5;
L2=0.41; %secundario
N2=300;
R2=1.4;
M=1.176; %inducción mutua
Us=50.2; %fuente de corriente alterna
w=2*pi*60;

i1=@(x)  Us*(1i*w*L2+R2+x)./((R1+1i*w*L1)*(1i*w*L2+R2+x)+w^2*M^2);
i2=@(x) 1i*Us*w*M./((R1+1i*w*L1)*(1i*w*L2+R2+x)+w^2*M^2);
I1=@(x) abs(i1(x));
I2=@(x) abs(i2(x));
figure %intensidades I1 e I2
hold on
fplot(I1,[0,100])
fplot(I2,[0,100])
hold off
grid on
xlabel('R_L')
ylabel('I_1, I_2')
legend('I_1', 'I_2', 'location', 'best')
title('Intensidades en el primario y secundario')

figure %diferencia de potencial en el secundario
V=@(x) abs(i2(x).*x);
fplot(V,[0,100])
grid on
xlabel('R_L')
ylabel('V')
title('ddp en el secundario')

figure %energía por unidad de tiempo
ang1=@(x) angle(i1(x));
producida=@(x) Us*I1(x).*cos(ang1(x)); 
consumida=@(x) (I2(x).^2).*x;
hold on
yyaxis left
fplot(producida,[0,100])
fplot(consumida,[0,100])
ylabel('Potencia')
yyaxis right
rendimiento=@(x) consumida(x)./producida(x);
fplot(rendimiento,[0,100])
ylabel('Rendimiento')
hold off
grid on
xlabel('R_L')
title('Potencia, producida, consumida y redimiento')

Representamos las amplitudes de las intensidades I₁ e I₂ en función de la resistencia R_Ldel circuito (dispositivo) conectado al secundario

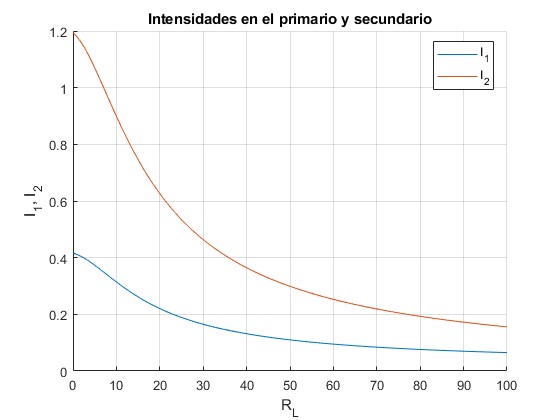
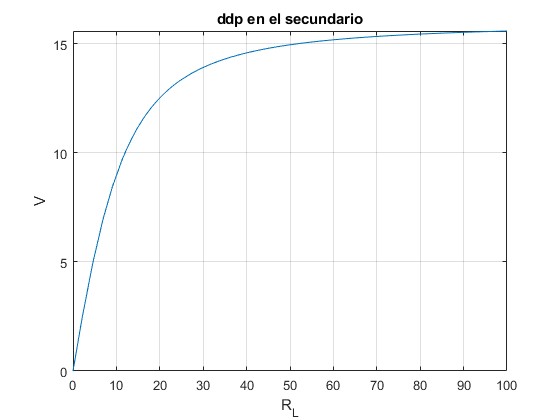
Representamos la diferencia de potencial en el secundario I₂R_L en función de la resistencia R_L

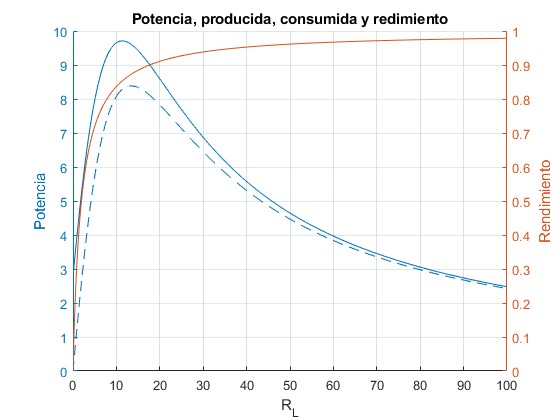
Representmos la potencia (energía por unidad de tiempo) producida en el circuito primario, la consumida en el circuito secundario y el redimiento del transformador

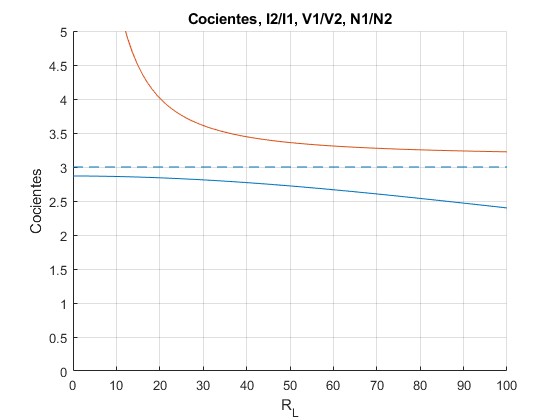
Representamos el cociente I₂/I₁, V₁/V₂ y la recta N₁/N₂ en función de R_L.

L1=3.69; %primario
N1=900;
R1=4.5;
L2=0.41; %secundario
N2=300;
R2=1.4;
M=1.176; %inducción mutua
Us=50.2; %fuente de corriente alterna
w=2*pi*60;

i1=@(x)  Us*(1i*w*L2+R2+x)./((R1+1i*w*L1)*(1i*w*L2+R2+x)+w^2*M^2);
i2=@(x) 1i*Us*w*M./((R1+1i*w*L1)*(1i*w*L2+R2+x)+w^2*M^2);
I_r=@(x) abs(i2(x)./i1(x));
hold on
fplot(I_r,[0,100])
V_r=@(x) Us./abs(i2(x).*x);
fplot(V_r,[0,100])
line([0,100],[N1/N2, N1/N2],'lineStyle','--')
grid on
ylim([0,5])
xlabel('R_L')
ylabel('Cocientes')
title('Cocientes, I2/I1, V1/V2, N1/N2')

Coeficiente de acoplamiento

Supongamos que el circuito primario y el secundario no tienen resistencias. Las ecuaciones que los describen son

${\displaystyle \{\begin{array}{l}{L}_1\frac{d{i}_1}{dt}-M\frac{d{i}_2}{dt}=U_s\\ L_2\frac{d{i}_2}{dt}-M\frac{d{i}_1}{dt}=0\end{array}}$

Multiplicamos la primera por i₁, la segunda por i₂ y sumamos

${\displaystyle \begin{array}{l}{L}_1{i}_1\frac{d{i}_1}{dt}+L_2{i}_2\frac{d{i}_2}{dt}-M{i}_1\frac{d{i}_2}{dt}-M{i}_2\frac{d{i}_1}{dt}=U_s{i}_1\\ \frac{d}{dt}\left(\frac{1}{2}{L}_1{i}_1^2+\frac{1}{2}{L}_2{i}_2^2-M{i}_1{i}_2\right)=U_s{i}_1\end{array}}$

Entre paréntesis, los dos primeros términos son las energías almacenadas por las dos bobinas Li²/2, el tercer término corresponde al acoplamiento. La cantidad entre parétesis es positiva o nula

${\displaystyle \begin{array}{l}\frac{1}{2}{L}_1{i}_1^2+\frac{1}{2}{L}_2{i}_2^2-M{i}_1{i}_2\ge 0\\ \frac{1}{2}{\left(\sqrt{L_1}{i}_1-\sqrt{L_2}{i}_2\right)}^2+i_1{i}_2\left(\sqrt{L_1{L}_2}-M\right)\ge 0\end{array}}$

El primer término es positivo, el segundo será positivo o nulo

${\displaystyle \sqrt{L_1{L}_2}-M\ge 0}$

Se define el coeficiente de acoplamiento como el cociente

${\displaystyle k=\frac{M}{\sqrt{L_1{L}_2}},0\le k\le 1}$

k=1, corresponde a un acoplamiento ideal y k=0, a una falta de acoplamiento entre los dos circuitos

Se conecta el primario a una fuente alterna

Para simplificar las ecuaciones, designamos R₂ a la resistencia total del secundario, la suma de la resistencia externa R_L y de la propia de la bobina que hasta ahora hemos denominado R₂

El sistema de dos ecuaciones es

${\displaystyle \begin{array}{l}{i}_1{R}_1+L_1\frac{d{i}_1}{dt}-M\frac{d{i}_2}{dt}=V_0\sin \left(\omega t\right)\\ i_2{R}_2+L_2\frac{d{i}_2}{dt}-M\frac{d{i}_1}{dt}=0\end{array}}$

Derivamos la primera respecto del tiempo y utilizamos la segunda y su derivada respecto de tiempo, para eliminar las derivadas de i₁ en la primera

${\displaystyle \begin{array}{l}{R}_1\frac{d{i}_1}{dt}+L_1\frac{d^2{i}_1}{d{t}^2}-M\frac{d^2{i}_2}{d{t}^2}=V_0\omega \cos \left(\omega t\right)\\ \{\begin{array}{l}M\frac{d{i}_1}{dt}=i_2{R}_2+L_2\frac{d{i}_2}{dt}\\ M\frac{d^2{i}_1}{d{t}^2}=R_2\frac{d{i}_2}{dt}+L_2\frac{d^2{i}_2}{d{t}^2}\end{array}\\ \left(L_1{L}_2-M^2\right)\frac{d^2{i}_2}{d{t}^2}+\left(R_1{L}_2+R_2{L}_1\right)\frac{d{i}_2}{dt}+R_1{R}_2{i}_2=M{V}_0\omega \cos \left(\omega t\right)\\ a_1\frac{d^2{i}_2}{d{t}^2}+a_2\frac{d{i}_2}{dt}+a_3{i}_2=a_4\cos \left(\omega t\right),\{\begin{array}{l}{a}_1=L_1{L}_2-M^2\\ a_2=R_1{L}_2+R_2{L}_1\\ a_3=R_1{R}_2\\ a_4=M{V}_0\omega \end{array}\end{array}}$

La solución de la ecuación diferencial homogénea describe el estado transitorio y la solución particular, el estado estacionario, que es el que nos interesa

${\displaystyle \begin{array}{l}{i}_2(t)=A\sin \left(\omega t\right)+B\cos \left(\omega t\right)\\ \frac{d{i}_2}{dt}=\omega \left(A\cos \left(\omega t\right)-B\sin \left(\omega t\right)\right)\\ \frac{d^2{i}_2}{d{t}^2}=-{\omega }^2\left(A\sin \left(\omega t\right)+B\cos \left(\omega t\right)\right)\end{array}}$

Introducimos en la ecuación diferencial

${\displaystyle \begin{array}{l}-a_1{\omega }^2\left(A\sin \left(\omega t\right)+B\cos \left(\omega t\right)\right)+a_2\omega \left(A\cos \left(\omega t\right)-B\sin \left(\omega t\right)\right)+a_3\left(A\sin \left(\omega t\right)+B\cos \left(\omega t\right)\right)=a_4\cos \left(\omega t\right)\\ \left(-A{a}_1{\omega }^2-B{a}_2\omega +a_{3}A\right)\sin \left(\omega t\right)+\left(-a_1{\omega }^{2}B+a_2\omega A+a_{3}B-a_4\right)\cos \left(\omega t\right)=0\\ \{\begin{array}{l}-A{a}_1{\omega }^2-B{a}_2\omega +a_{3}A=0\\ -a_1{\omega }^{2}B+a_2\omega A+a_{3}B=a_4\end{array}\\ A=\frac{a_4{a}_2\omega }{{\left(a_2\omega \right)}^2+{\left(a_3-a_1{\omega }^2\right)}^2},B=\frac{a_4\left(a_3-a_1{\omega }^2\right)}{{\left(a_2\omega \right)}^2+{\left(a_3-a_1{\omega }^2\right)}^2}\end{array}}$

Calculamos la amplitud I₀ y el desfase φ

${\displaystyle \begin{array}{l}{i}_2(t)=I_0\sin \left(\omega t+\phi \right)=I_0\sin \left(\omega t\right)\cos \phi +I_0\cos \left(\omega t\right)\sin \phi ,\\ \{\begin{array}{l}A=I_0\cos \phi \\ B=I_0\sin \phi \end{array},\{\begin{array}{l}{I}_0=\sqrt{A^2+B^2}\\ \tan \phi =\frac{B}{A}\end{array}\\ I_0=\frac{a_4\sqrt{a_1^2{\omega }^4+\left(a_2^2-2a_3{a}_1\right){\omega }^2+a_3^2}}{{\left(a_2\omega \right)}^2+{\left(a_3-a_1{\omega }^2\right)}^2},\tan \phi =\frac{a_3-a_1{\omega }^2}{a_2\omega }\end{array}}$

Sustituimos a₁, a₂, a₃ y a₄ por sus valores

${\displaystyle \begin{array}{l}{I}_0=\frac{M{V}_0\omega \sqrt{{\left(L_1{L}_2-M^2\right)}^2{\omega }^4+\left({\left(R_1{L}_2+R_2{L}_1\right)}^2-2R_1{R}_2\left(L_1{L}_2-M^2\right)\right){\omega }^2+R_1^2{R}_2^2}}{{\left(\left(R_1{L}_2+R_2{L}_1\right)\omega \right)}^2+{\left(R_1{R}_2-\left(L_1{L}_2-M^2\right){\omega }^2\right)}^2}=\\ \frac{M{V}_0\omega }{\sqrt{{\left(L_1{L}_2-M^2\right)}^2{\omega }^4+\left(R_1^2{L}_2^2+R_2^2{L}_1^2+2R_1{R}_2{M}^2\right){\omega }^2+R_1^2{R}_2^2}}\\ \tan \phi =\frac{R_1{R}_2-\left(L_1{L}_2-M^2\right){\omega }^2}{\left(R_1{L}_2+R_2{L}_1\right)\omega }\end{array}}$

En un transformador se cumple aproximadamente que M²≈L₁L₂

${\displaystyle \begin{array}{l}{I}_0\approx \frac{V_0\omega \sqrt{L_1{L}_2}}{\sqrt{{\left(R_1{L}_2+R_2{L}_1\right)}^2{\omega }^2+R_1^2{R}_2^2}}\\ \tan \phi \approx \frac{R_1{R}_2}{\left(R_1{L}_2+R_2{L}_1\right)\omega }\end{array}}$

Cuando la frecuencia angular ω se hace grande I₀ tiende hacia el valor

${\displaystyle \underset{\omega \to \infty }{\lim }{I}_0=\frac{V_0\sqrt{L_1{L}_2}}{R_1{L}_2+R_2{L}_1}}$

Gráficas

Los datos del transformador son los siguientes:

• Primario: autoinducción L₁=3.69 H, resistencia, R₁=4.5 Ω
• Secundario: autoinducción L₂=0.41 H, resistencia, R₂=1.4+20 Ω

Representamos la amplitud de la intensidad en el secundario, I₀ en función de la frecuencia angular ω de la fuente alterna conectada al primario

L1=3.69; %primario
R1=4.5;
L2=0.41; %secundario
R2=1.4+20; %resistencia total en el secundario
V0=50.2; %fuente de corriente alterna

I2=@(x) V0*x*sqrt(L1*L2)./sqrt((R1*L2+R2*L1)^2*x.^2+R1^2*R2^2);
fplot(I2,[0,10])
If= V0*sqrt(L1*L2)/(R1*L2+R2*L1);
line([0,10],[If,If],'lineStyle','--')
grid on
ylim([0,1])
xlabel('\omega')
ylabel('I_2')
title('Intensidad en el secundario')

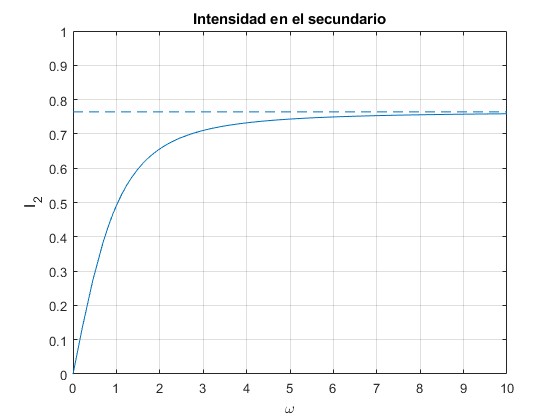
La amplitud tiende hacia un valor constante cuando se incrementa la frecuencia ω. La amplitud final disminuye con la resistencia R₂

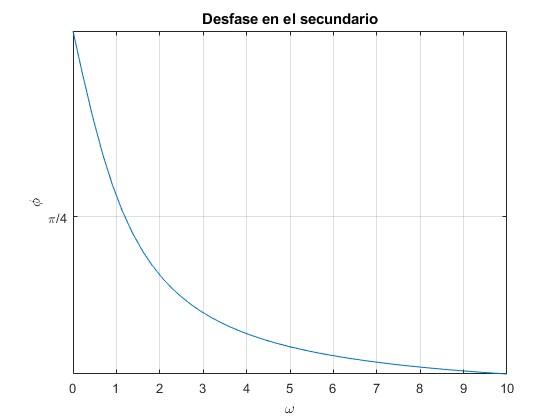
Representamos la fase de la intensidad en el secundario, φ en función de la frecuencia angular ω de la fuente alterna conectada al primario

L1=3.69; %primario
R1=4.5;
L2=0.41; %secundario
R2=1.4+20;  %resistencia total en el secundario
V0=50.2; %fuente de corriente alterna

phi=@(x) atan(R1*R2./((R1*L2+R2*L1)*x));
fplot(phi,[eps,10])
grid on
set(gca,'YTick',0:pi/4:pi)
set(gca,'YTickLabel',{'0','\pi/4','\pi/2','3\pi/4','\pi'})
xlabel('\omega')
ylabel('\phi')
title('Desfase en el secundario')

Referencias

Fabio S El Hage, Fabio P B Vieira, Rodrigo Carareto. Deriving and validating an electrodynamic model of a voltage transformer from scratch. Eur. J. Phys. 42 (2021) 035207

J. Pierrus. Solved Problems in Classical Electromagnetism. Analytical and numerical solutions with comments. Oxford University Press (2018). Question 6.23, pp. 327-328.

B. Evstatiev, Mutually coupled inductors. Lecture notes in Theory of electrical engineering