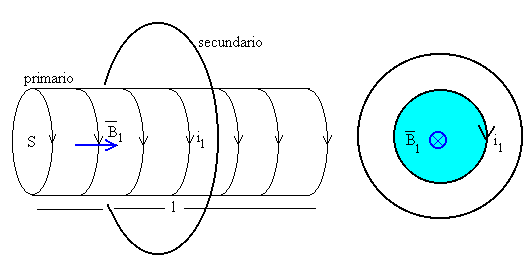
Supongamos que tenemos dos circuitos acoplados formados por una espira y un solenoide, tal como se muestra en la figura.

El solenoide está formado N espiras, de longitud l y de sección S recorrido por una corriente de intensidad i₁. Supondremos que el solenoide es muy largo en comparación con su radio.

Denominaremos circuito primario al solenoide y secundario a la espira.

1. El campo magnético creado por el solenoide (primario) suponemos que es uniforme y paralelo a su eje y cuyo módulo hemos obtenido aplicando la ley de Ampère

${\displaystyle B_1=\frac{{\mu }_{0}N{i}_1}{l}}$

2. Este campo atraviesa la sección de la espira (secundario), el flujo de dicho campo a través de la espira vale.

${\displaystyle {\Phi }_2=\overrightarrow{B_1}·\overrightarrow{S}=\frac{{\mu }_{0}NS}{l}{i}_1}$

S es la sección del solenoide, no de la espira, ya que hemos supuesto que fuera del solenoide no hay campo magnético.

3. Se denomina coeficiente de inducción mutua M₁₂ al cociente entre el flujo a través del secundario Φ₂ y la intensidad en el primario i₁.

${\displaystyle M_{12}=\frac{{\Phi }_2}{i_1}=\frac{{\mu }_{0}NS}{l}={\mu }_{0}nS}$

Donde n=N/l es el número de espiras por unidad de longitud

El coeficiente de inducción mutua solamente depende de la geometría de los circuitos y de su posición relativa. La unidad de medida del coeficiente de inducción mutua se llama henry, abreviadamente H, en honor a Joseph Henry.

Denominaremos ahora, circuito primario a la espira de radio a y secundario al solenoide de radio b y de n espiras por unidad de longitud.

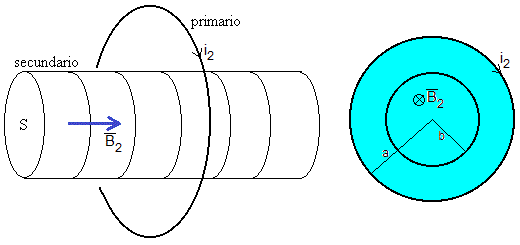
1. El campo magnético creado por la espira tiene simetría cilíndrica, su componente radial B_ρ y su componente a lo largo del eje Z, B_z son

${\displaystyle \begin{array}{l}\xi =\frac{\rho }{a},\zeta =\frac{z}{a}\hfill \\ \begin{array}{l}{B}_{\rho }=\frac{{\mu }_{0}i}{2\pi a}\frac{\varsigma }{\xi \sqrt{({(1+\xi )}^2+{\varsigma }^2)}}\left(-K(m)+\frac{2-m}{2-2m}E(m)\right)\\ B_z=\frac{{\mu }_{0}i}{2\pi a}\frac{1}{\xi \sqrt{{\left(1+\xi \right)}^2+{\varsigma }^2}}\left(\frac{m-2\xi +m\xi }{2-2m}E(m)+\xi K(m)\right)\end{array}\hfill \\ m=\frac{4\xi }{{\left(1+\xi \right)}^2+{\varsigma }^2}\hfill \end{array}}$

2. Este campo atraviesa la sección de una espira del solenoide situada a una altura z, el flujo de dicho campo a través de dicha espira vale.



${\displaystyle {\displaystyle \int \overrightarrow{B}·\overrightarrow{dS}}={\displaystyle \underset{0}{\overset{b}{\int }}{B}_z\left(2\pi \rho ·d\rho \right)}}$

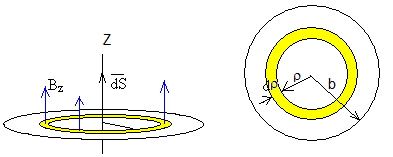
El flujo del campo magnético producido por la espira de radio a a través de todas las espiras del solenoide es

${\displaystyle {\Phi }_1={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\left({\displaystyle \underset{0}{\overset{b}{\int }}{B}_z\left(2\pi \rho ·d\rho \right)}\right)}n·dz=2n\pi a^3{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{b/a}{\int }}{B}_z\xi ·d\xi }·}d\zeta =4n\pi a^3{\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{b/a}{\int }}{B}_z\xi d\xi }}·d\zeta }$

3. Se denomina coeficiente de inducción mutua M₂₁ al cociente entre el flujo a través del secundario Φ₁ y la intensidad en el primario i₂.

${\displaystyle M_{21}=\frac{{\Phi }_1}{i_2}=2{\mu }_{0}n{a}^2{\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{b/a}{\int }}\frac{1}{\sqrt{{\left(1+\xi \right)}^2+{\varsigma }^2}}\left(\frac{m-2\xi +m\xi }{2-2m}E(m)+\xi K(m)\right)d\xi }}·d\zeta }$

Ejemplo

Calculamos la integral doble mediante el procedimiento integral2 de MATLAB para varios valores del coeficiente b/a

${\displaystyle \frac{M_{21}}{{\mu }_{0}n{a}^2}=\frac{{\mu }_{0}n\pi b^2}{{\mu }_{0}n{a}^2}=\pi {\left(\frac{b}{a}\right)}^2}$

y lo comparamos con π(b/a)²

function mutua
    for r=0.1:0.1:0.7 %r=b/a
        k=2*integral2(@f, 0, r, 0,100);
        S=pi*r^2;
        disp([r, k, S])
    end
    
    function Bz=f(y,z)
        m=4*y./((1+y).^2+z.^2);
        [K,E]=ellipke(m);
        Bz=(y.*K+((m-2*y+y.*m).*E)./(2-2*m))./sqrt((1+y).^2+z.^2);
    end
end

    0.1000    0.0314    0.0314
    0.2000    0.1257    0.1257
    0.3000    0.2827    0.2827
    0.4000    0.5026    0.5027
    0.5000    0.7854    0.7854
    0.6000    1.1309    1.1310
    0.7000    1.5393    1.5394

Los resultados coinciden

f.e.m. inducida

Cuando la intensidad de la corriente i₁ en el primario cambia con el tiempo, se induce en el secundario una f.e.m. V₂ que se opone a los cambios de flujo.

Aplicamos la ley de Faraday. derivando el flujo que atraviesa el secundario Φ₂=M·i₁ respecto del tiempo

${\displaystyle V_2=-\frac{d{\Phi }_2}{dt}=-M\frac{d{i}_1}{dt}}$

La fem en el secundario V₂ siempre actúa en el sentido que se opone a la variación de la intensidad de la corriente que circula por el primario.

El transformador

Hace algo más de un siglo que se inventó este dispositivo que ha hecho posible la distribución de energía eléctrica a todos los hogares, industrias, etc. Si no fuera por el transformador tendría que acortarse la distancia que separa los generadores de electricidad de los consumidores.

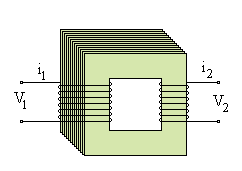
El transformador lo encontramos en muchos lugares: para cargar el móvil, en las lámparas de bajo consumo, cargadores de pilas, en sótanos de edificios, en las centrales hidroeléctricas, etc. Su tamaño puede variar desde muy pequeños a enormes transformadores que pueden pesar más de 500 Tm.

El primario del transformador tiene N₁ espiras y el secundario N₂, comparten el mismo núcleo de hierro que asegura que el flujo φ a través de cada espira sea el mismo.

Si la corriente en el primario i₁ varía con el tiempo se produce en el secundario una fem inducida V₂.

${\displaystyle V_2=-\frac{d{\Phi }_2}{dt}=-\frac{d\left(N_2\phi \right)}{dt}=-N_2\frac{d\phi }{dt}}$

Si cambiamos los papeles de modo que el secundario pase a ser primario y viceversa

${\displaystyle V_1=-\frac{d{\Phi }_1}{dt}=-\frac{d\left(N_1\phi \right)}{dt}=-N_1\frac{d\phi }{dt}}$

Dividiendo ambas expresiones, obtenemos la relación de transformación

${\displaystyle \frac{V_2}{V_1}=\frac{N_2}{N_1}}$

Por ejemplo, si el secundario tiene N₂=5N₁ resulta que V₂=5V₁, dicho transformador aumenta en el secundario la tensión del primario y se llama transformador elevador. Para que un transformador sea reductor deberá tener menos espiras en el secundario que en el primario.

Si no hay pérdidas de energía en el proceso de transformación por corrientes de Foucault y otras pérdidas en el núcleo laminado de hierro, se cumplirá que la energía por unidad de tiempo (potencia) en el primario será la misma que en el secundario

P=i₁·V₁=i₂·V₂

Ejemplo

Una radio funciona con corriente de 9 V y 360 mA. Si el primario del transformador tiene 440 vueltas. ¿Cuántas hemos de ponerle al secundario?

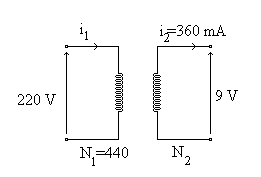
Transformamos una tensión en el primario de 220 voltios a 9 voltios en el secundario

${\displaystyle \frac{9}{220}=\frac{N_2}{440}{N}_2=18}$

Si no hay pérdidas de energía, la potencia en el primario debe ser igual a la del secundario.

220·i₁=9·360 por lo que i₁=14.7 mA

Al aumentar la tensión disminuye la intensidad, este hecho, es empleado para transportar la electricidad a grandes distancias reduciendo las pérdidas por efecto Joule. En una central eléctrica, el generador está conectado al primario de un transformador de elevación de tensión, mientras que las líneas de transporte de electricidad están conectadas al secundario. En el primario hay una intensidad alta, con un valor moderado de la tensión. En el secundario, la tensión se eleva hasta cerca de 500 000 V y por consiguiente, la corriente en el secundario se reduce en la misma proporción. Como las pérdidas por efecto Joule son proporcionales al cuadrado de la intensidad, al disminuir la intensidad en el secundario se reducen las pérdidas por calentamiento.

En el otro extremo de la línea, debe utilizarse un transformador reductor para disminuir la tensión, de forma que podamos usar la electricidad de forma más cómoda y segura, y dispongamos de una corriente de mayor intensidad.

Experiencias en el laboratorio

Horno de inducción

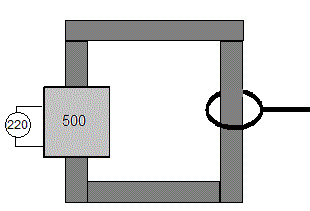
El transformador consiste en una bobina primaria de 500 espiras concectada a la corriente alterna y una bobina secundaria de una espira preparada en forma de ranura, representa un modelo de horno de inducción. Se calcula la intensidad en el secundario midiendo la intensidad en el primario y aplicando la relación de transformación. Se coloca una cinta de estaño sobre la ranura y vemos que se funde.

${\displaystyle \begin{array}{l}\frac{V_2}{220}=\frac{1}{500}{V}_2=0.4\\ i_1{V}_1=i_2{V}_2{i}_2=\frac{220}{0.4}{i}_1=550i_1\end{array}}$

Salto de chispa entre dos alambres

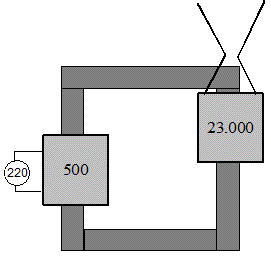
En el primario se coloca una bobina de 500 espiras conectada a la corriente alterna (220 V), en el secundario una bobina de 23.000 espiras. Se calcula la tensión en el secundario mediante la relación de transformación. La salida del secundario son dos alambres que se pueden aproximar a pocos milímetros de distancia. Se observa un salto de chispa entre los dos alambres.

${\displaystyle \frac{V_2}{220}=\frac{23000}{500}{V}_2=10120V}$

Medida del coeficiente de inducción mutua

Disponemos de un generador de señales sinosuidales, cuya frecuencia establecemos alrededor de 3000 Hz mediante la rueda. Un amperímetro para medir la amplitud de la intensidad I₀ de la corriente que circula por el primario. Un multímetro digital que nos mide la amplitud de la fem en el secundario V₀ y la frecuencia f de la corriente alterna.

El primario es un largo solenoide de N₁/L₁=485 vueltas/metro y el secundario, alguno de los solenoides más pequeños que se introducen completamente en el solenoide grande, de N₂ vueltas y diámetro de la sección d₂, o área $S_2=\frac{1}{4}\pi d_2^2$

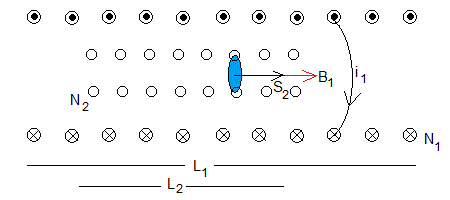
1. Campo magnético producido por el primario (solenoide exterior) recorrido por una intensidad i₁

${\displaystyle B_1={\mu }_0\frac{N_1}{L_1}{i}_1}$

dirección paralelo al eje del solenoide, sentido (regla de la mano derecha, para espiras)

2. Flujo a través del secundario (solenoide interior)

${\displaystyle {\Phi }_2=\overrightarrow{B}\cdot \overrightarrow{S}=\left({\mu }_0\frac{N_1}{L_1}{i}_1\right)\left(N_2{S}_2\right)\cos 0=\left({\mu }_0\frac{N_1{N}_2}{L_1}{S}_2\right)i_1=M{i}_1}$

M es el coeficiente de inducción mutua que queremos determinar

3. Por el primario circula una corriente alterna i₁=I₀·sin(ωt), ω=2πf, siendo f la frecuencia en Hz. Se produce una fem en el secundario

${\displaystyle V_2=-\frac{d{\Phi }_2}{dt}=-M\frac{d{i}_1}{dt}=-2\pi fM{I}_0\cos \left(2\pi ft\right)=-V_0\cos \left(2\pi ft\right)}$

4. Medida del coeficiente de inducción mutua M

Se mide I₀ con el amperímetro, V₀ y f con el multímetro digital

${\displaystyle M=\left(\frac{V_0}{I_0}\right)\frac{1}{2\pi f}}$

Coeficiente del inducción mutua M a partir de los características de los solenoides

${\displaystyle M={\mu }_0\frac{N_1}{L_1}{N}_2{S}_2}$

Primario: N₁/L₁=485 vueltas/metro. μ₀=4π·10^-7

Medida de μ₀

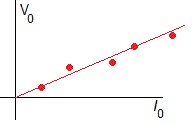
Otra experiencia interesante sería la medida de la constante μ₀, fijando la frecuencia f y variando la corriente I₀. Utilizamos un dispositivo formado por un solenoide interior, N₂, S₂ y exterior N₁, L₁, conocidos. La fem en el secundario de amplitud V₀ es proporcional a la corriente en el primario de amplitud I₀. A partir de los pares de datos de la experiencia (I₀, V₀), calculamos la pendiente de la recta de ajuste que es proporcional a μ₀

${\displaystyle V_0=2\pi f\left({\mu }_0\frac{N_1}{L_1}{N}_2{S}_2\right)I_0}$

Fuerza entre solenoides

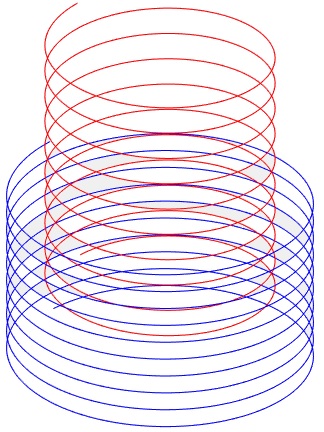
Supongamos que se introduce parcialemente un solenoide dentro de otro de diámetro mayor. Por los dos solenoides circulan corrientes en el mismo sentido, produciéndose una fuerza que hace que el solenoide interior se introduzca en el exterior

Hay dos procedimientos para calcular la fuerza:

• Conociendo el coeficiente de inducción mutua

${\displaystyle F=i_1{i}_2\frac{dM}{dx}}$

• Conociendo la energía asociada al campo magnético producido por los dos solenoides

${\displaystyle F=\frac{d{E}_B}{dx}}$

El código que representa los dos solenoides, interior y exterior es

hold on
t=0:0.05:20*pi;
x=sin(t);
y=cos(t);
z=0.2*t;
plot3(x,y,z,'b')
t=0:0.05:20*pi;
x=0.75*sin(t);
y=0.75*cos(t);
z=5+0.3*t;
plot3(x,y,z,'r')
hold off
view(-44,24)
axis off

Coeficiente de inducción mutua

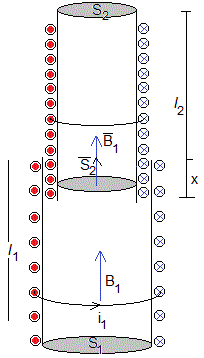
El solenoide exterior de longitud l₁, tiene N₁ espiras de sección S₁, es recorrido por una corriente i₁ en el sentido indicado

El solenoide interior de longitud l₂, tiene N₂ espiras de sección S₂, está parcialmente introducido en el solenoide exterior, tal como se muestra en la figura

1. Campo magnético producido por el primario (solenoide exterior) recorrido por una intensidad i₁

${\displaystyle B_1={\mu }_0\frac{N_1}{l_1}{i}_1}$

dirección paralelo al eje del solenoide, sentido (regla de la mano derecha, para espiras)

2. Flujo a través e las N₂x/l₂ espiras del secundario que están dentro del primario.

${\displaystyle {\Phi }_2=\overrightarrow{B}\cdot \overrightarrow{S}=\left({\mu }_0\frac{N_1}{l_1}{i}_1\right)\left(N_2\frac{x}{l_2}\right)S_2\cos 0=\left({\mu }_0\frac{N_1{N}_2}{l_1{l}_2}{S}_{2}x\right)i_1=M{i}_1}$

M es el coeficiente de inducción mutua que queremos determinar

Por el solenoide interior circula una corriente i₂ en el mismo sentido que i₁, ambos solenoides se atraen con una fuerza

${\displaystyle F=i_1{i}_2\frac{dM}{dx}=i_1{i}_2\left({\mu }_0\frac{N_1{N}_2}{l_1{l}_2}\right)S_2}$

Energía asociada al campo magnético

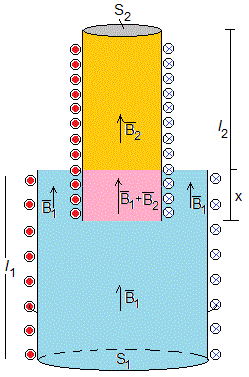
La energía asociada al campo magnético producido por ambos solenoides es

${\displaystyle E_B=\frac{1}{2{\mu }_0}{\displaystyle \int B^{2}dV}}$

La integral se extiende a todo el espacio donde hay campo magnético no nulo.

1. El volumen del solenoide interior es S₂l₂, en la porción l₂-x de ese volumen existe un campo B₂=μ₀N₂i₂/l₂, la energía almacenada en el volumen S₂(L₂-x) es

${\displaystyle \frac{1}{2{\mu }_0}{B}_2^2\left(S_2(l_2-x)\right)=\frac{1}{2{\mu }_0}{\left({\mu }_0\frac{N_2}{l_2}{i}_2\right)}^2\left(S_2(l_2-x)\right)}$

2. En la intersección de los dos solenoides x, en el volumen S₂x, el campo magnético está producido por los dos solenoides que tienen la misma dirección y sentido B₁+B₂, la energía asociada a este campo magnético en ese volumen es

${\displaystyle \frac{1}{2{\mu }_0}{\left(B_1+B_2\right)}^2\left(S_{2}x\right)=\frac{1}{2{\mu }_0}{\left({\mu }_0\frac{N_1}{l_1}{i}_1+{\mu }_0\frac{N_2}{l_2}{i}_2\right)}^2\left(S_{2}x\right)}$

3. En el volumen del solenoide exterior, S₁l₁, excepto en la intersección S₂x, el campo magnético es B₁, la energía asociada a este campo magnético en ese volumen es

${\displaystyle \frac{1}{2{\mu }_0}{B}_1^2\left(S_1{l}_1-S_{2}x\right)=\frac{1}{2{\mu }_0}{\left({\mu }_0\frac{N_1}{l_1}{i}_1\right)}^2\left(S_1{l}_1-S_{2}x\right)}$

Sumamos las tres contribuciones a la energía del campo magnético producido por los dos solenoides

${\displaystyle E_B=\frac{1}{2}{\mu }_0\left\{{\left(\frac{N_1}{l_1}{i}_1\right)}^2\left(S_1{l}_1\right)+{\left(\frac{N_2}{l_2}{i}_2\right)}^2\left(S_2{l}_2\right)+2\left(\frac{N_1}{l_1}{i}_1\right)\left(\frac{N_2}{l_2}{i}_2\right)\left(S_{2}x\right)\right\}}$

La fuerza se calcula derivando respecto de x

${\displaystyle F=\frac{d{E}_B}{dx}=i_1{i}_2\left({\mu }_0\frac{N_1{N}_2}{l_1{l}_2}\right)S_2}$

Obtenemos el mismo resultado

Referencias

Paul Lorrain, Dale R. Corson. Campos y Ondas Electromagnéticas, Selecciones Científicas (1972) págs. 383-386

Antonio J Barbero, José A Manzanares, Salvador Mafé. Induced EMF in a solenoid: a simple quantitative verification of Faraday's law. Physics Education Vol 29, (2) March 1994, pp. 102-105

PHYWE. Magnetic induction

Ian C Malcolm. Mutual inductance between an infinite solenoid and a surrounding loop—A paradox resolved. Am. J. Phys. 92(6), June 2024. pp. 473-475