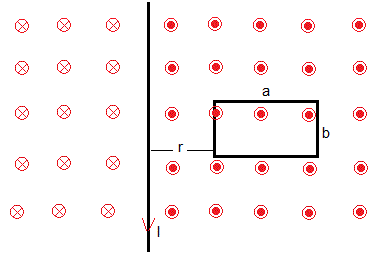
Consideremos una corriente rectilínea muy larga por la que circula una corriente I(t) en el sentido indicado, que dista r de una espira rectangular de lados a y b hecha con un cable de resistencia R.

Corriente inducida

El flujo del campo magnético producido por la corriente rectilínea a través de la espira es

${\displaystyle \Phi ={\displaystyle \underset{S}{\int }\overrightarrow{B}·\overrightarrow{dS}}={\displaystyle \underset{r}{\overset{r+a}{\int }}\left(\frac{{\mu }_{0}I}{2\pi x}\right)\left(b·dx\right)\cos 0=}\frac{{\mu }_{0}I}{2\pi }b\ln \left(\frac{r+a}{r}\right)}$

El coeficiente de inducción mutua es

${\displaystyle M(r)=\frac{\Phi }{I}=\frac{{\mu }_{0}b}{2\pi }\ln \left(\frac{r+a}{r}\right)}$

Hay que sumar a esta flujo, el flujo propio, producido por la corriente inducida i en la espira

${\displaystyle \Phi =M(r)I+Li}$

La ecuación del circuito es

${\displaystyle \begin{array}{l}iR=-\frac{d\Phi }{dt}\\ -iR=M(r)\frac{dI}{dt}+I\frac{dM(r)}{dt}+L\frac{di}{dt}\\ -iR=M(r)\frac{dI}{dt}+I\frac{dM(r)}{dr}\frac{dr}{dt}+L\frac{di}{dt}\end{array}}$

La autoinducción L de la espira es independiente de su posición

Vamos a considerar dos casos

• La espira permenece fija en la posición r₀

${\displaystyle L\frac{di}{dt}+iR=-M(r_0)\frac{dI}{dt}}$

Supongamos que la corriente rectilínea I(t) tiene la siguiente forma

${\displaystyle I(t)=I_0\left(\frac{1+\tanh (kt)}{2}\right)}$

hold on
for k=[1,2]
    f=@(t) (1+tanh(k*t))/2;
    fplot(f,[-3,3],'displayName',num2str(k))
end
hold off
grid on
legend('-DynamicLegend','location','best')
xlabel('t')
ylabel('I(t)')
title('Corriente')



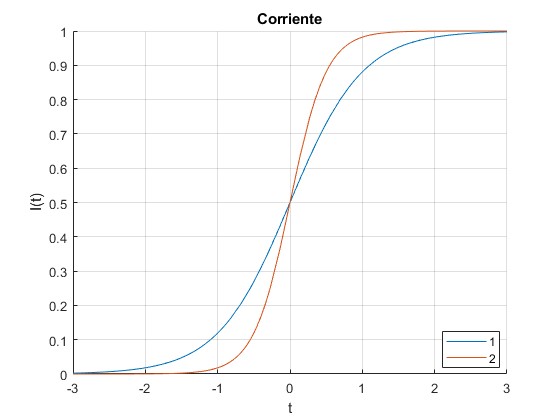
Se trata de una corriente que pasa de 0 a I₀ en un tiempo tanto más corto, cuanto mayor sea el parámetro k

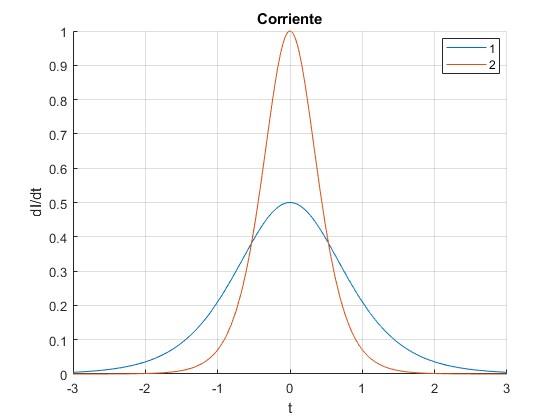
La derivada dI/dt tiene un valor distinto de cero en un intervalo tanto más pequeño, cuanto mayor sea k

${\displaystyle \frac{dI}{dt}=\frac{I_0}{2}\frac{k}{{\cosh }^2(kt)}}$

hold on
for k=[1,2]
    f=@(t) (k/2)./cosh(k*t).^2;
    fplot(f,[-3,3] ,'displayName',num2str(k))
end
hold off
grid on
legend('-DynamicLegend','location','best')
xlabel('t')
ylabel('dI/dt')
title('Corriente')



La ecuación del circuito tiene la forma

${\displaystyle \frac{di}{d\tau }+ai=-\frac{b}{{\cosh }^2\tau },\tau =kt}$

Resolvemos la ecuación diferencial por procedimientos numéricos con la siguiente condición inicial: en el instante τ=0, la intesidad es nula, i=0

a=0.2;
b=2;
f=@(t,x) -a*x(1)-b/cosh(t)^2; 
[t,x]=ode45(f,[0,30],0); 
plot(t,x)
grid on
xlabel('t')
ylabel('i');
title('Corriente inducida')



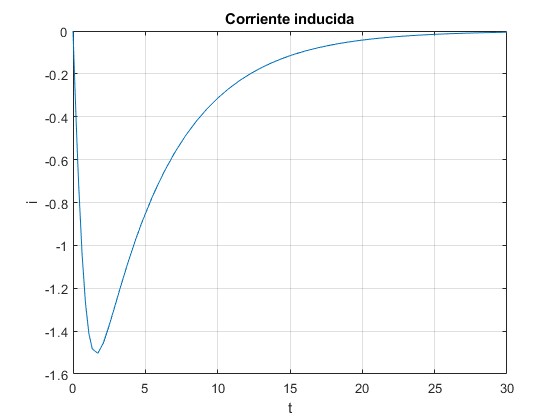
La corriente inducida en la espira es negativa (sentido de las agujas del reloj), se opone al incremento del flujo del campo magnético producido por la corriente rectilínea

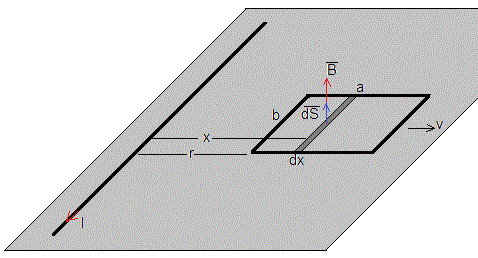
• La espira se mueve hacia la derecha, la intensidad I(t) de la corriente rectilínea permenece constante

La ecuación del circuito es

${\displaystyle \begin{array}{l}-iR=I\frac{dM(r)}{dr}\frac{dr}{dt}+L\frac{di}{dt}\\ L\frac{di}{dt}+iR=I\frac{{\mu }_{0}b}{2\pi }\frac{a}{r\left(r+a\right)}\frac{dr}{dt}\end{array}}$

Si la resistencia es cero, R=0, se puede integrar

${\displaystyle \begin{array}{l}Li=I\frac{{\mu }_{0}ba}{2\pi }{\displaystyle \underset{r_0}{\overset{r}{\int }}\frac{dr}{r(r+a)}}\\ Li=I\frac{{\mu }_{0}b}{2\pi }{\displaystyle \underset{r_0}{\overset{r}{\int }}\left(\frac{1}{r}-\frac{1}{r+a}\right)dr}\\ Li=I\frac{{\mu }_{0}b}{2\pi }\left(\ln \left(\frac{r}{r+a}\right)-\ln \left(\frac{r_0}{r_0+a}\right)\right)=I\frac{{\mu }_{0}b}{2\pi }\ln \left(\frac{r\left(r_0+a\right)}{r_0\left(r+a\right)}\right)\\ Li=I\frac{{\mu }_{0}b}{2\pi }\ln \left(\frac{1+a/r_0}{1+a/r}\right)\end{array}}$

Se ha supuesto que la corriente i en la espira es nula en el instante t=0, i(0)=0, cuando la espira se encuentra a una distancia r₀ de la corriente rectilínea.

Para r>r₀ la intensidad i es positiva (sentido contrario a las agujas del reloj) ya que disminuye el flujo del campo magnético producido por la corriente rectilínea

Si la resistencia es cero, R=0 el flujo total, $\Phi =M(r)I+Li$, permanece constante

Fuerzas sobre la espira

La fuerza que ejerce el campo magnético sobre una porción de corriente de intensidad i es

${\displaystyle \overrightarrow{F}=i{\displaystyle \underset{A}{\overset{B}{\int }}\left({\widehat{u}}_t\times \overrightarrow{B}\right)dl}}$

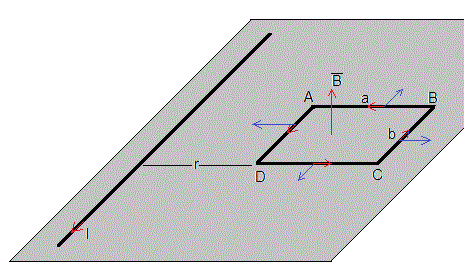
Las fuerzas sobre los lados AB y CD son iguales y de sentido contrario y no afectan al movimiento de la espira

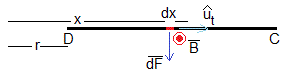
La fuerza sobre un elemento de corriente dx situado a una distancia x de la corriente rectilínea es

${\displaystyle dF=i\frac{{\mu }_{0}I}{2\pi x}dx}$

La fuerza sobre el lado CD es

${\displaystyle F_{CD}=i\frac{{\mu }_{0}I}{2\pi }{\displaystyle \underset{r}{\overset{r+a}{\int }}\frac{dx}{x}}=i\frac{{\mu }_{0}I}{2\pi }\ln \frac{r+a}{a}}$

Calculamos las fuerzas que ejerce el campo magnético producido por la corriente rectilínea sobre los lados AD y BC

${\displaystyle \begin{array}{l}{F}_{AD}=i\frac{{\mu }_{0}I}{2\pi r}b\\ F_{BC}=i\frac{{\mu }_{0}I}{2\pi \left(r+a\right)}b\end{array}}$

La dirección y sentido de la fuerzas vienen determinadas por el producto vectorial $$ {\widehat{u}}_t\times \overrightarrow{B}$$

La fuerza resultante sobre la espira es

${\displaystyle F=F_{BC}-F_{AD}=i\frac{{\mu }_{0}I}{2\pi }\left(\frac{1}{r+a}-\frac{1}{r}\right)b=-i\frac{{\mu }_{0}I}{2\pi }\frac{ab}{r\left(r+a\right)}}$

La fuerza es atractiva, F<0. Si la intensidad I de la corriente rectilínea cambiase de signo, la fuerza sería repulsiva, F>0

Referencias

Markus Zahn. Electromagnetic field theory. A problem solving approach. pp. 397-399