Solenoide

En la página titulada Autoinducción. Circuito R-L, hemos calculado el coeficiente de autoinducción de un solenoide de longitud l, sección S y de N espiras

${\displaystyle L=\frac{{\mu }_0{N}^2}{l}S}$

Para un solenoide de n espiras por unidad de longitud, longitud l=2b y radio a de su sección

${\displaystyle L={\mu }_0{n}^2(2b)\pi a^2}$

Para calcularlo, se ha supuesto que el campo magnético en el interior del solenoide es constante y paraleo al eje. En realidad, el campo disminuye a la mitad en los extremos del solenoide

En el artículo citado en las referencias se proporciona una fórmula exacta, sin demostración

${\displaystyle \begin{array}{l}L=\frac{8}{3}{\mu }_0{\left(na\right)}^2\left\{\sqrt{a^2+b^2}C\left(k_{\mathrm{0,}}\mathrm{1,1,2}{k}_0^2\right)-a\right\}\\ k_0=\frac{b}{\sqrt{a^2+b^2}}\end{array}}$

Donde C es una integral elíptica completa generalizada, que se ha definido en la página titulada, Componentes del campo magnético producido por un solenoide. En esta página, se proporciona el código de la función integral_eliptica para calcularla

Ejemplo

Calculamos el coeficiente de autoinducción de un solenoide PHYWE de n=485 vueltas/m, 2b=0.75 m, y radio a=0.035 m. Una fotografía de este solenoide se puede ver en la página titulada Inducción mutua.

a=0.035; %radio
b=0.75/2; %longitud 2b
n=485; %vueltas/m
 
L=4*pi*1e-7*n^2*2*b*pi*a^2; %aproximado
k0=b/sqrt(a^2+b^2);
LL=8*4*pi*1e-7*(n*a)^2*(sqrt(a^2+b^2)*integral_eliptica(k0,1,1,2*k0^2)-a)/3;
disp([L,LL])

   1.0e-03 *    0.8532    0.8203

El cálculo aproximado da 0.85 mH y el exacto 0.82 mH.

Espira circular

En la página titulada, Campo magnético producido por una corriente circular en un punto fuera de su eje, calculamos las componentes radial, B_ρ y a lo largo del eje B_z del campo magnético producido por una espira de radio a recorrida por una intensidad i, en un punto fuera del eje, en términos de integrales elípticas.

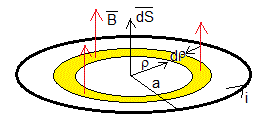
En la figura, se muestra como se calcula el flujo propio Φ del campo magnético producido por la espira a través de su sección circular. El campo magnético para z=0, es vertical, la componente B_ρ=0

${\displaystyle \begin{array}{l}{B}_z(\rho )=\frac{{\mu }_{0}i}{2\pi }\frac{a}{{(2a\rho )}^{3/2}}\sqrt{2m}\left(a\frac{m}{2-2m}E(m)+\rho K(m)-\rho \frac{2-m}{2-2m}E(m)\right)\\ m=\frac{4a\rho }{{(a+\rho )}^2}\end{array}}$

En términos de la variable adimensional x=ρ/a

${\displaystyle \begin{array}{l}{B}_z(x)=\frac{{\mu }_{0}i}{4\pi a{x}^{3/2}}\sqrt{m}\left(\frac{m-(2-m)x}{2-2m}E(m)+xK(m)\right)\\ m=\frac{4x}{{\left(1+x\right)}^2}\end{array}}$

El campo B_z crece con x, para x→1 que se hace infinito. Para evitarlo, hay que tener en cuenta el radio r del cable con el que está hecha la espira.

El flujo propio Φ se obtiene, calculando numéricamente la integral

${\displaystyle \begin{array}{l}\Phi ={\displaystyle \underset{0}{\overset{a-r}{\int }}{B}_z(\rho )2\pi \rho ·d\rho =}{a}^2{\displaystyle \underset{0}{\overset{1-r/a}{\int }}{B}_z(x)2\pi x·dx=}\\ \frac{{\mu }_{0}i}{2}a{\displaystyle \underset{0}{\overset{1-r/a}{\int }}\sqrt{\frac{m}{x}}\left(\frac{m-(2-m)x}{2-2m}E(m)+xK(m)\right)}dx\end{array}}$

Si es una bobina de N espiras apretadas, el campo magnético se multiplica por N y la superficie por N espiras, el flujo propio es proporcional a N². El coeficiente de autoinducción es

${\displaystyle L=\frac{N^2\Phi }{i}={\mu }_0{N}^{2}a{\displaystyle \underset{0}{\overset{1-r/a}{\int }}\frac{1}{1+x}\left(\frac{m-(2-m)x}{2-2m}E(m)+xK(m)\right)}dx}$

Una fórmula aproximada es

${\displaystyle L\approx {\mu }_0{N}^{2}a\left(\ln \frac{8a}{r}-2\right)}$

Fuente: O. L. de Lange, J. Pierrus. Solved Problems in Classical Mechanics. Analytical and numerical solutions with comments. Question 5.18, pp. 278

Ejemplo

Calculamos el coeficiente de autoinducción de la bobina PASCO, EM-6723A, cuyas características son, radio interior 10.06 cm, radio exterior 11.37 cm y número de vueltas 500.

Consideramos la bobina como una espira de radio medio, a=(11.37+10.06)/2=10.715 cm. El radio equivalente del cable con el que se fabrica la espira sería, la mitad del espesor, r=(11.37-10.06)/2=0.655 cm.

N=500; %número de espiras
a=10.715/100; %radio medio
r=0.655/100; %radio del cable equivalente
 
xx=linspace(0,1-r/a, 200);
y=zeros(1,length(xx));
i=1;
for x=xx
    m=4*x/(1+x)^2;
    [K,E]=ellipke(m);
    y(i)=((m-(2-m)*x)*E/(2-2*m)+x*K)/(1+x);
    i=i+1;
end
L=4*pi*1e-7*N^2*a*trapz(xx,y);
L1=4*pi*1e-7*N^2*a*(log(8*a/r)-2); %aproximada
disp([L,L1])

0.0928    0.0968

El resultado es L=92.8 mH

Espira rectangular

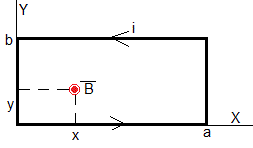
Sea una espira rectangular de lados a y a recorrida por una intensidad i en el sentido contrario a las agujas del reloj. Calculamos el campo magnético producido en el punto (x,y), en el interior del rectángulo, producido por la corriente que circula por cada uno de los lados. Dichos campos magnéticos tienen la misma dirección y sentido, perpendicular al plano de la espira y hacia afuera, por tanto, se suman sus módulos

Calcularemos el flujo propio Φ a través de la espira rectangular, suponiendo que el cable con el que se ha fabricado la espira, tiene radio r mucho más pequeño que sus dimensiones a y b. El coeficiente de autoinducción es el cociente L=Φ/i.

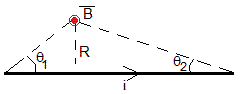
El campo magnético producido por un segmento rectilíneo de corriente se ha calculado en la página titulada, Campo magnético producido por una corriente rectilínea indefinida

${\displaystyle B=\frac{{\mu }_{0}i}{4\pi R}(\cos {\theta }_1+\cos {\theta }_2)}$

cuya dirección es perpendicular al plano que contiene la corriente y el punto y cuyo sentido se determina aplicando la regla de la mano derecha.

El campo magnético producido en P por cada uno de los cuatro lados de la espira rectangular y el flujo propio Φ, son

${\displaystyle \begin{array}{l}{B}_1=\frac{{\mu }_{0}i}{4\pi y}\left(\frac{x}{\sqrt{y^2+x^2}}+\frac{a-x}{\sqrt{y^2+{\left(a-x\right)}^2}}\right)\\ B_2=\frac{{\mu }_{0}i}{4\pi \left(a-x\right)}\left(\frac{x}{\sqrt{{\left(a-x\right)}^2+x^2}}+\frac{b-y}{\sqrt{{\left(a-x\right)}^2+{\left(b-y\right)}^2}}\right)\\ B_3=\frac{{\mu }_{0}i}{4\pi \left(b-y\right)}\left(\frac{a-x}{\sqrt{{\left(b-y\right)}^2+{\left(a-x\right)}^2}}+\frac{x}{\sqrt{{\left(b-y\right)}^2+x^2}}\right)\\ B_4=\frac{{\mu }_{0}i}{4\pi x}\left(\frac{y}{\sqrt{x^2+y^2}}+\frac{b-y}{\sqrt{x^2+{\left(b-y\right)}^2}}\right)\end{array}}$

El campo magnético total producido por la espira rectangular en el punto P (x,y) es

${\displaystyle \begin{array}{l}B(x,y)=\frac{{\mu }_{0}i}{4\pi }\left(\sqrt{\frac{1}{y^2}+\frac{1}{x^2}}+\sqrt{\frac{1}{y^2}+\frac{1}{{\left(a-x\right)}^2}}+\sqrt{\frac{1}{{\left(b-y\right)}^2}+\frac{1}{x^2}}+\sqrt{\frac{1}{{\left(b-y\right)}^2}+\frac{1}{{\left(a-x\right)}^2}}\right)\\ \Phi ={\displaystyle \underset{r}{\overset{b-r}{\int }}{\displaystyle \underset{r}{\overset{a-r}{\int }}B(x,y)dx·dy}}\end{array}}$

El flujo propio Φ es la suma de cuatro integrales dobles. Por simetría, los flujos de los campos B₁ y B₃ producidos por las corrientes horizontales, serán iguales. Lo mismo ocurrirá para los flujos de los campos B₂ y B₄ producidos por las corrientes verticales

Para resolver la integral doble, precisamos del resultado de dos integrales

• En la primera, hacemos un cambio de variable

${\displaystyle \begin{array}{l}{\displaystyle \int \sqrt{\frac{c^2}{z^2}+1}·dz}=\{\begin{array}{l}\sinh t=\frac{c}{z}\\ \cosh t·dt=-\frac{c}{z^2}dz\end{array}\\ -c{\displaystyle \int \frac{{\cosh }^{2}t}{{\sinh }^{2}t}}dt=-c{\displaystyle \int \left(1+\frac{1}{{\sinh }^{2}t}\right)}dt=-c\left(t-\coth t\right)=c\left(-a\sinh \left(\frac{c}{z}\right)+\sqrt{\frac{z^2}{c^2}+1}\right)\end{array}}$

• En la segunda, integramos por partes

${\displaystyle \begin{array}{l}{\displaystyle \int \text{arcsinh}z·dz={\displaystyle \int \ln \left(z+\sqrt{z^2+1}\right)}}·dz=,\{\begin{array}{l}u=\ln \left(z+\sqrt{z^2+1}\right),du=\frac{dz}{\sqrt{z^2+1}}\\ dv=dz,v=z\end{array}\\ z·\text{arcsinh}z-\sqrt{z^2+1}\end{array}}$

Calculamos la integral doble del primer sumando

${\displaystyle {\displaystyle \underset{r}{\overset{b-r}{\int }}{\displaystyle \underset{r}{\overset{a-r}{\int }}\sqrt{\frac{1}{y^2}+\frac{1}{x^2}}·dx·dy}}}$

Integramos con respecto de x

${\displaystyle \begin{array}{l}\frac{1}{y}{\displaystyle \int \sqrt{\frac{y^2}{x^2+1}}·dx}=,\{\begin{array}{l}c=y\\ z=x\end{array}\\ \text{-arcsinh}\left(\frac{y}{x}\right)+\sqrt{\frac{x^2}{y^2}+1}\end{array}}$

Evaluamos la integral entre los límites r y a-r

${\displaystyle {\displaystyle \underset{r}{\overset{a-r}{\int }}\sqrt{\frac{1}{y^2}+\frac{1}{x^2}}·dx=\text{-arcsinh}\left(\frac{y}{a-r}\right)+\sqrt{\frac{{\left(a-r\right)}^2}{y^2}+1}}\text{+arcsinh}\left(\frac{y}{r}\right)-\sqrt{\frac{r^2}{y^2}+1}}$

Integramos respecto de y los cuatro términos

• Primer término

${\displaystyle \begin{array}{l}-{\displaystyle \int \text{arcsinh}\left(\frac{y}{a-r}\right)·dy=,\{\begin{array}{l}z=\frac{y}{a-r}\\ dz=\frac{dy}{a-r}\end{array}}\\ -\left(a-r\right)\left\{\left(\frac{y}{a-r}\right)\text{arcsinh}\left(\frac{y}{a-r}\right)-\sqrt{{\left(\frac{y}{a-r}\right)}^2+1}\right\}\end{array}}$

Evaluamos la integral entre los límites r y b-r

${\displaystyle {\displaystyle \underset{r}{\overset{b-r}{\int }}\text{arcsinh}\left(\frac{y}{a-r}\right)·dy}=-\left(b-r\right)\text{arcsinh}\left(\frac{b-r}{a-r}\right)+\left(a-r\right)\sqrt{{\left(\frac{b-r}{a-r}\right)}^2+1}+r·\text{arcsinh}\left(\frac{r}{a-r}\right)-\left(a-r\right)\sqrt{{\left(\frac{r}{a-r}\right)}^2+1}}$

• Tercer término

${\displaystyle \begin{array}{l}-{\displaystyle \int \text{arcsinh}\left(\frac{y}{r}\right)·dy=,\{\begin{array}{l}z=\frac{y}{r}\\ dz=\frac{dy}{r}\end{array}}\\ r\left\{\frac{y}{r}\text{arcsinh}\left(\frac{y}{r}\right)-\sqrt{{\left(\frac{y}{r}\right)}^2+1}\right\}\end{array}}$

Evaluamos la integral entre los límites r y b-r

${\displaystyle {\displaystyle \underset{r}{\overset{b-r}{\int }}\text{arcsinh}\left(\frac{y}{r}\right)·dy}=\left(b-r\right)\text{arcsinh}\left(\frac{b-r}{r}\right)-r\sqrt{{\left(\frac{b-r}{r}\right)}^2+1}-r·\text{arcsinh}\left(1\right)+r\sqrt{2}}$

• Segundo término

${\displaystyle \begin{array}{l}-{\displaystyle \int \sqrt{\frac{{\left(a-r\right)}^2}{y^2}+1}·dy=,\{\begin{array}{l}c=a-r\\ z=y\end{array}}\\ \left(a-r\right)\left\{\text{-arcsinh}\left(\frac{a-r}{y}\right)+\sqrt{{\left(\frac{y}{a-r}\right)}^2+1}\right\}\end{array}}$

Evaluamos la integral entre los límites r y b-r

${\displaystyle {\displaystyle \underset{r}{\overset{b-r}{\int }}\sqrt{\frac{{\left(a-r\right)}^2}{y^2}+1}·dy}=-\left(a-r\right)\text{arcsinh}\left(\frac{a-r}{b-r}\right)+\left(a-r\right)\sqrt{{\left(\frac{b-r}{a-r}\right)}^2+1}+\left(a-r\right)\text{arcsinh}\left(\frac{a-r}{r}\right)-\left(a-r\right)\sqrt{{\left(\frac{r}{a-r}\right)}^2+1}}$

• Cuarto término

${\displaystyle \begin{array}{l}-{\displaystyle \int \sqrt{\frac{r^2}{y^2}+1}}dy=,\{\begin{array}{l}c=r\\ z=y\end{array}\\ -r\left\{\text{-arcsinh}\left(\frac{r}{y}\right)+\sqrt{{\left(\frac{y}{r}\right)}^2+1}\right\}\end{array}}$

Evaluamos la integral entre los límites r y b-r

${\displaystyle {\displaystyle \underset{r}{\overset{b-r}{\int }}\sqrt{\frac{r^2}{y^2}+1}·dy}=r·\text{arcsinh}\left(\frac{r}{b-r}\right)-r\sqrt{{\left(\frac{b-r}{r}\right)}^2+1}-r·\text{arcsinh}\left(1\right)+r\sqrt{2}}$

La contribución al flujo propio Φ del primer término de B(x,y) es proporcional a

${\displaystyle \begin{array}{l}{\displaystyle \underset{r}{\overset{b-r}{\int }}{\displaystyle \underset{r}{\overset{a-r}{\int }}\sqrt{\frac{1}{y^2}+\frac{1}{x^2}}·dx·dy}}=\\ -\left(b-r\right)\text{arcsinh}\left(\frac{b-r}{a-r}\right)+\left(a-r\right)\sqrt{{\left(\frac{b-r}{a-r}\right)}^2+1}+r·\text{arcsinh}\left(\frac{r}{a-r}\right)-\left(a-r\right)\sqrt{{\left(\frac{r}{a-r}\right)}^2+1}+\\ \left(b-r\right)\text{arcsinh}\left(\frac{b-r}{r}\right)-r\sqrt{{\left(\frac{b-r}{r}\right)}^2+1}-r·\text{arcsinh}\left(1\right)+r\sqrt{2}+\\ -\left(a-r\right)\text{arcsinh}\left(\frac{a-r}{b-r}\right)+\left(a-r\right)\sqrt{{\left(\frac{b-r}{a-r}\right)}^2+1}+\left(a-r\right)\text{arcsinh}\left(\frac{a-r}{r}\right)-\left(a-r\right)\sqrt{{\left(\frac{r}{a-r}\right)}^2+1}+\\ r·\text{arcsinh}\left(\frac{r}{b-r}\right)-r\sqrt{{\left(\frac{b-r}{r}\right)}^2+1}-r·\text{arcsinh}\left(1\right)+r\sqrt{2}\end{array}}$

Agrupamos términos

${\displaystyle \begin{array}{l}{\displaystyle \underset{r}{\overset{b-r}{\int }}{\displaystyle \underset{r}{\overset{a-r}{\int }}\sqrt{\frac{1}{y^2}+\frac{1}{x^2}}·dx·dy}}=\\ r·\text{arcsinh}\left(\frac{r}{a-r}\right)+r·\text{arcsinh}\left(\frac{r}{b-r}\right)+\left(a-r\right)\text{arcsinh}\left(\frac{a-r}{r}\right)+\\ \left(b-r\right)\text{arcsinh}\left(\frac{b-r}{r}\right)-\left(a-r\right)\text{arcsinh}\left(\frac{a-r}{b-r}\right)-\left(b-r\right)\text{arcsinh}\left(\frac{b-r}{a-r}\right)\\ -2r·\text{arcsinh}\left(1\right)+2r\sqrt{2}-2\sqrt{{\left(b-r\right)}^2+r^2}-2\sqrt{r^2+{\left(a-r\right)}^2}+2\sqrt{{\left(b-r\right)}^2+{\left(a-r\right)}^2}\end{array}}$

Este resultado, multiplicado por el factor μ₀/(4π), es la contribución al flujo propio Φ del primer término de B(x,y). El lector puede comprobar, repitiendo cálculos similares, que las otras contribuciones producen el mismo resultado

${\displaystyle \begin{array}{l}{\displaystyle \underset{r}{\overset{b-r}{\int }}{\displaystyle \underset{r}{\overset{a-r}{\int }}\sqrt{\frac{1}{y^2}+\frac{1}{{\left(a-x\right)}^2}}·dx·dy}}=\\ {\displaystyle \underset{r}{\overset{b-r}{\int }}{\displaystyle \underset{r}{\overset{a-r}{\int }}\sqrt{\frac{1}{{\left(b-y\right)}^2}+\frac{1}{x^2}}·dx·dy}}=\\ {\displaystyle \underset{r}{\overset{b-r}{\int }}{\displaystyle \underset{r}{\overset{a-r}{\int }}\sqrt{\frac{1}{{\left(b-y\right)}^2}+\frac{1}{{\left(a-x\right)}^2}}·dx·dy}}=\end{array}}$

El flujo propio Φ del campo magnético producido por la espira rectangular es

${\displaystyle \Phi ={\displaystyle \underset{r}{\overset{b-r}{\int }}{\displaystyle \underset{r}{\overset{a-r}{\int }}B(x,y)dx·dy}}=\frac{{\mu }_{0}i}{\pi }\left\{\begin{array}{l}r·\text{arcsinh}\left(\frac{r}{a-r}\right)+r·\text{arcsinh}\left(\frac{r}{b-r}\right)+\left(a-r\right)\text{arcsinh}\left(\frac{a-r}{r}\right)+\\ \left(b-r\right)\text{arcsinh}\left(\frac{b-r}{r}\right)-\left(a-r\right)\text{arcsinh}\left(\frac{a-r}{b-r}\right)-\left(b-r\right)\text{arcsinh}\left(\frac{b-r}{a-r}\right)\\ -2r·\text{arcsinh}\left(1\right)+2r\sqrt{2}-2\sqrt{{\left(b-r\right)}^2+r^2}-2\sqrt{r^2+{\left(a-r\right)}^2}\\ +2\sqrt{{\left(b-r\right)}^2+{\left(a-r\right)}^2}\end{array}\right\}}$

El coeficiente de autoinducción es L=Φ/i

${\displaystyle L=\frac{{\mu }_0}{\pi }\left\{\begin{array}{l}r·\text{arcsinh}\left(\frac{r}{a-r}\right)+r·\text{arcsinh}\left(\frac{r}{b-r}\right)+\left(a-r\right)\text{arcsinh}\left(\frac{a-r}{r}\right)+\\ \left(b-r\right)\text{arcsinh}\left(\frac{b-r}{r}\right)-\left(a-r\right)\text{arcsinh}\left(\frac{a-r}{b-r}\right)-\left(b-r\right)\text{arcsinh}\left(\frac{b-r}{a-r}\right)\\ -2r·\text{arcsinh}\left(1\right)+2r\sqrt{2}-2\sqrt{{\left(b-r\right)}^2+r^2}-2\sqrt{r^2+{\left(a-r\right)}^2}\\ +2\sqrt{{\left(b-r\right)}^2+{\left(a-r\right)}^2}\end{array}\right\}}$

Aproximaciones

El radio r del cable del que está hecha la espira es mucho menor que sus dimensiones a y b.

${\displaystyle L\approx \frac{{\mu }_0}{\pi }\left\{\begin{array}{l}r·\text{arcsinh}\left(\frac{r}{a}\right)+r·\text{arcsinh}\left(\frac{r}{b}\right)+a·\text{arcsinh}\left(\frac{a}{r}\right)+\\ b\text{·arcsinh}\left(\frac{b}{r}\right)-a·\text{arcsinh}\left(\frac{a}{b}\right)-b·\text{arcsinh}\left(\frac{b}{a}\right)\\ -2r·\text{arcsinh}\left(1\right)+2r\sqrt{2}-2\sqrt{b^2+r^2}-2\sqrt{r^2+a^2}\\ +2\sqrt{b^2+a^2}\end{array}\right\}}$

Otras aproximaciones

${\displaystyle \begin{array}{l}r·\text{arcsinh}\left(\frac{r}{a}\right)=r\ln \left(\frac{r}{a}+\sqrt{{\left(\frac{r}{a}\right)}^2+1}\right)=r\ln \left(\frac{r+\sqrt{a^2+r^2}}{a}\right)\approx r\ln \left(\frac{r+a}{a}\right)\approx r\ln \left(1\right)=0\\ a·\text{arcsinh}\left(\frac{a}{r}\right)=a\ln \left(\frac{a}{r}+\sqrt{{\left(\frac{a}{r}\right)}^2+1}\right)=a\ln \left(\frac{a+\sqrt{a^2+r^2}}{r}\right)\approx a\ln \left(\frac{2a}{r}\right)\\ -2r·\ln \left(1+\sqrt{2}\right)+2r\sqrt{2}\approx -r\\ -2\sqrt{b^2+r^2}\approx -2b\\ -2\sqrt{r^2+a^2}\approx -2a\end{array}}$

El resultado final, es la fórmula aproximada del coeficiente de autoindución de una espira rectangular

${\displaystyle L\approx \frac{{\mu }_0}{\pi }\left\{a·\ln \left(\frac{2a}{r}\right)+b·\ln \left(\frac{2b}{r}\right)-a\ln \left(\frac{a+\sqrt{a^2+b^2}}{b}\right)-b\ln \left(\frac{b+\sqrt{a^2+b^2}}{a}\right)-2(a+b)+2\sqrt{a^2+b^2}\right\}}$

Nota. El término -2(a+b) no parece correcto, debería ser -7(a+b)/4

Comparamos el resultado exacto y aproximado para una espira rectangular de dimensiones, a=40 cm, b=60 cm, el diámetro del cable es 2r=1 mm

r=1/2000; %radio del cable 1mm de diámetro
a=0.4; %lados
b=0.6;
%aproximado
L=4e-7*(-2*(a+b)+2*sqrt(a^2+b^2)-b*log((b+sqrt(b^2+a^2))/a)-
a*log((a+sqrt(b^2+a^2))/b)+b*log(2*b/r)+a*log(2*a/r));
%exacto
LL=4e-7*(-2*r*asinh(1)+2*r*sqrt(2)-2*sqrt((b-r)^2+r^2)-2*sqrt((a-r)^2+r^2)+
2*sqrt((b-r)^2+(a-r)^2)+r*asinh(r/(b-r))+(b-r)*asinh((b-r)/r)+r*asinh(r/(a-r))
-(b-r)*asinh((b-r)/(a-r))-(a-r)*asinh((a-r)/(b-r))+(a-r)*asinh((a-r)/r));
disp([L,LL]

1.0e-05 *    0.2439    0.2436

El resultado es muy parecido, 0.244·10^-5 H

Espira cuadrada

Para una espira cuadrada a=b

La fórmula exacta es

${\displaystyle \begin{array}{l}L=\frac{{\mu }_0}{\pi }2\left\{\begin{array}{l}r·\text{arcsinh}\left(\frac{r}{a-r}\right)+\left(a-r\right)\text{arcsinh}\left(\frac{a-r}{r}\right)+\\ -\left(a-r\right)\text{arcsinh}\left(1\right)\\ -r·\text{arcsinh}\left(1\right)+r\sqrt{2}-2\sqrt{{\left(a-r\right)}^2+r^2}\\ +\left(a-r\right)\sqrt{2}\end{array}\right\}=\\ L=\frac{{\mu }_0}{\pi }2\left\{\begin{array}{l}r·\text{arcsinh}\left(\frac{r}{a-r}\right)+\left(a-r\right)\text{arcsinh}\left(\frac{a-r}{r}\right)+\\ -a·\text{arcsinh}\left(1\right)-2\sqrt{{\left(a-r\right)}^2+r^2}+a\sqrt{2}\end{array}\right\}\end{array}}$

La fórmula aproximada con r<<a es

${\displaystyle \begin{array}{l}L\approx \frac{{\mu }_0}{\pi }2\left\{\begin{array}{l}r·\text{arcsinh}\left(\frac{r}{a}\right)+a·\text{arcsinh}\left(\frac{a}{r}\right)+\\ -a·\text{arcsinh}\left(1\right)-2\sqrt{a^2+r^2}+a\sqrt{2}\end{array}\right\}\approx \\ \frac{{\mu }_0}{\pi }2a\left\{0+\ln \left(\frac{a}{r}\right)+\ln (2)-\text{arcsinh}\left(1\right)-2+\sqrt{2}\right\}=\\ \frac{{\mu }_0}{\pi }2a\left\{\ln \left(\frac{a}{r}\right)-\text{0}\text{.7740}\right\}\end{array}}$

Comparamos el resultado exacto y aproximado para una espira cuadrada de dimensiones, a=40 cm, el diámetro del cable es 2r=1 mm

r=1/2000; %radio del cable 1 mm de diámetro
a=0.4; %lado

%aproximado
L=8e-7*a*(log(a/r)-0.7740);
%exacto
LL=8e-7*(r*asinh(r/(a-r))+(a-r)*asinh((a-r)/r)-a*asinh(1)-
2*sqrt((a-r)^2+r^2)+a*sqrt(2));
disp([L,LL])

1.0e-05 *    0.1891    0.1889

El resultado es muy parecido, 0.189·10^-5 H

Referencias

Norman Derby, Stanislaw Olbert. Cylindrical magnets and ideal solenoids. Am. J. Phys. 78 (3) March 2010, pp. 229-235