La experiencia consta de dos partes:

1. Se coloca una espira de radio igual al del anillo en el interior de un largo solenoide. Se hace circular una corriente alterna por el solenoide (primario), se observa en la pantalla del osciloscopio la fem producida en la espira (secundario)

2. Se sitúa el anillo en el interior del solenoide. Se hace circular la misma corriente alterna por el solenoide (primario), se mide la fem producida en el anillo (secundario). Se observa en la pantalla del osciloscopio un cambio en la amplitud y la fase. En la experiencia real, se sitúa el anillo en el interior de la espira, rodeándolo completamente, tal como se indica en la figura.

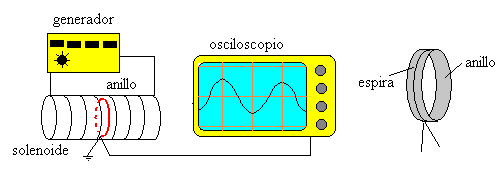
Comparando las amplitudes relativas y la diferencia fases de las representaciones de las dos fem en la pantalla de un osciloscopio, se determina la autoinducción del anillo.

f.em. inducida en la espira

Supongamos que el solenoide está formado N espiras, de longitud l recorrido por una corriente de intensidad i₁. Denominaremos circuito primario al solenoide y secundario a la espira.

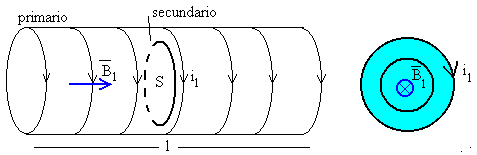
El campo magnético creado por el solenoide (primario) es uniforme y paralelo a su eje, se obtiene su módulo aplicando la ley de Ampère

${\displaystyle B_1=\frac{{\mu }_{0}N}{l}{i}_1}$

Este campo atraviesa la sección de la espira (secundario) de área S, el flujo de dicho campo a través de la espira vale.

${\displaystyle {\Phi }_e=\overrightarrow{B_1}·\overrightarrow{S}=\frac{{\mu }_{0}NS}{l}{i}_1}$

Cuando la intensidad de la corriente i₁ en el primario cambia con el tiempo, se induce en el secundario una fem V_e que se opone a los cambios de flujo. Aplicamos la ley de Faraday, derivando el flujo que atraviesa el secundario respecto del tiempo

${\displaystyle V_e=-\frac{d{\Phi }_e}{dt}=-\frac{{\mu }_{0}NS}{l}\frac{d{i}_1}{dt}}$

La fem en el secundario V_e siempre actúa en el sentido que se opone a la variación del flujo producido por el primario.

Si la corriente que circula por el primario i₁ varía con el tiempo de la forma

i₁=I₀·cos(ωt)

La fem producida en la espira es

${\displaystyle V_e=\frac{{\mu }_{0}NS}{l}{I}_0\omega ·\sin (\omega t)=V_0\sin (\omega t)}$

El anillo como circuito R-L en serie conectado a una fem alterna

El anillo tiene una autoinducción L y una resistencia R. Supongamos que el anillo es un circuito R-L en serie conectado a una fem alterna de la forma V_ε = V₀·sin(ωt).

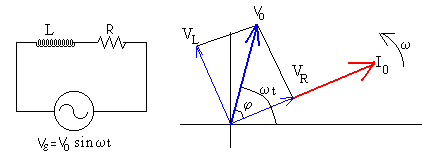
La diferencia de potencial en los extremos de la autoinducción L está adelantada 90º respecto de la intensidad que circula por ella. La relación de amplitudes es V_L=I₀·ω L.

La diferencia de potencial entre los extremos de la resistencia R está en fase con la intensidad. La relación de amplitudes es V_R=I₀·R.

Como vemos en la figura, la fem V_ε, está adelantada un ángulo φ respecto de la intensidad I_a.

${\displaystyle \begin{array}{l}\tan \phi =\frac{V_L}{V_R}=\frac{\omega L}{R}\\ V_0^2=V_R^2+V_L^2{I}_0=\frac{V_0}{\sqrt{R^2+{\omega }^2{L}^2}}\end{array}}$

La intensidad de la corriente inducida en el anillo en función del tiempo es

${\displaystyle I_a=\frac{V_0}{\sqrt{R^2+{\omega }^2{L}^2}}\sin (\omega t-\phi )}$

La fem medida en la espira que rodea el anillo, está en fase con la intensidad.

${\displaystyle V_a=V_{0a}\sin (\omega t-\phi )V_{0a}=\frac{V_0·R}{\sqrt{R^2+{\omega }^2{L}^2}}}$

Resistencia del anillo

Supongamos que tenemos un anillo hecho de un material de resistividad ρ en forma toroidal de diámetro medio D, cuya sección es un círculo de diámetro d, siendo d<<D.

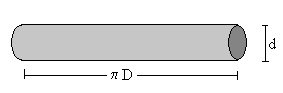
La ley de Ohm establece que la resistencia es

${\displaystyle R=\rho \frac{l}{A}=\rho \frac{\pi D}{\pi \frac{d^2}{4}}=\rho \frac{4D}{d^2}}$

En esta tabla se proporcionan datos acerca de la resistividad de algunos conductores metálicos.

Fuente: Koshkin N. I, Shirkévich M.G.. Manual de Física elemental. Edt Mir (1975), pág. 139.

La autoinducción del anillo

Existe una fórmula que nos permite calcular la autoinducción L de un anillo de forma toroidal de diámetro medio D, cuya sección es un círculo de diámetro d

${\displaystyle L={\mu }_0\frac{D}{2}\left(\ln \frac{8D}{d}-\frac{7}{4}\right)}$

Medida de la autoinducción

En la gráfica se comparan las fem en la espira y en el anillo, que nos va a permitir calcular la autoinducción L del anillo por dos procedimientos

• Comparando las amplitudes V₀ y V_0a

• Midiendo la diferencia de fase

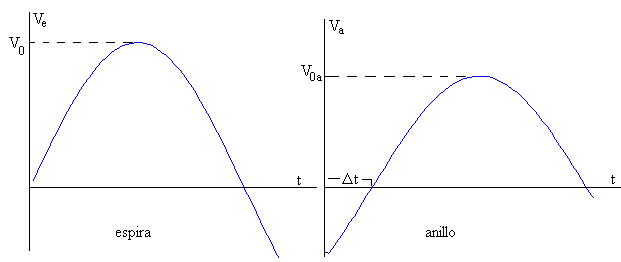
Primer procedimiento

Conocidas

• la amplitud V₀ de la fem en la espira en unidades arbitrarias.
• la amplitud V_0a de la fem en el anillo.

Se calcula el cociente entre las dos amplitudes

${\displaystyle \frac{V_{0a}}{V_0}=\frac{R}{\sqrt{R^2+{\omega }^2{L}^2}}=\cos \phi }$

Para la frecuencia angular ω=2πf y conocido el valor de la resistencia R se despeja el coeficiente de autoinducción L.

Segundo procedimiento.

Se mide el ángulo φ de desfase entre la fem en la espira y la fem del anillo. Para ello, anotamos el intervalo de tiempo Δt que trascurre hasta que la curva que describe la fem en el anillo cruza por primera vez el eje horizontal.

${\displaystyle \begin{array}{l}\phi =\omega ·\Delta t\\ \tan \phi =\frac{\omega L}{R}\end{array}}$

Conocido el valor de la resistencia R, calculamos la autoinducción L y la comparamos con el valor proporcionado por la fórmula de la autoinducción de un anillo

Actividades

Se introduce

• El diámetro D medio del anillo circular en cm, en el control titulado Diámetro anillo.
• El diámetro d de la sección trasversal circular del anillo en mm, en el control titulado Diámetro sección.
• El material del que está hecho el anillo, en el control titulado Material
• La frecuencia f en Hz producida por el generador de señales, en el control titulado Frecuencia.

1. Se activa el botón de radio titulado Espira.
2. Se pulsa el botón titulado Nuevo

En la parte izquierda, se representa el solenoide y la espira (en trazo fino).

• El movimiento de los puntos, representan la corriente en el solenoide (primario).

• El movimiento de los puntos, representan la corriente inducida en la espira (secundario)

• Una flecha en el centro de la espira señala el módulo y el sentido del campo magnético.

En la parte derecha, se representa la fem en la espira en función del tiempo. Cuando se acaba la representación gráfica, se anota la amplitud V₀ en unidades arbitrarias.

3. Se activa el botón titulado Anillo
4. Se pulsa el botón titulado Nuevo

El anillo está aparece dibujado en trazo grueso.

Se representa la fem en la espira en función del tiempo. Cuando se acaba la representación gráfica, se anota la amplitud V_0a.

Se calcula la resistencia R del anillo empleando la ley de Ohm, se despeja el valor de la autoinducción L.

Utilizando el botón titulado Ⅱ, se mide en la representación gráfica de la fem del anillo el tiempo Δt que tarda en atravesar por primera vez el eje horizontal.

Se calcula el desfase φ. Conocida la resistencia R del anillo, se despeja la autoinducción L.

Ejemplo:

Datos del anillo

• Material del anillo, aluminio, resistividad 0.028·10^-6 Ω·m
• Diámetro del toroide, D=20 cm=0.2 m
• Diámetro de la sección, d=1.5 mm=0.0015 m

Resistencia

${\displaystyle R=\rho \frac{4D}{d^2}=2.8·{10}^{-8}\frac{4·0.2}{{0.0015}^2}=9.96·{10}^{-3}\Omega }$

Si la frecuencia angular es ω=2π·1000 rad/s

• Se mide la amplitud de la fem en la espira es V₀=2.22.
• Se mide la amplitud de la fem en el anillo es V_0a=2.05

Calculamos la autoinducción

${\displaystyle L=\frac{R}{\omega }\sqrt{{\left(\frac{V_0}{V_{0a}}\right)}^2-1}=6.58·{10}^{-7}\text{H}}$

Medimos el intervalo de tiempo Δt=0.065·10^-3 s que tarda la fem en cruzar por primera vez el eje horizontal. Calculamos el desfase

φ=ω·Δt=2·π·1000·0.065·10^-3=0.41 rad

${\displaystyle L=\frac{R\tan \phi }{\omega }=6.85·{10}^{-7}\text{H}}$

El valor calculado mediante la fórmula de la autoinducción de un anillo es

${\displaystyle L=4\pi ·{10}^{-7}\frac{0.2}{2}\left(\ln \frac{8·0.2}{0.0015}-\frac{7}{4}\right)=6.56·{10}^{-7}\text{H}}$

Referencias

Mak S Y, Young K. Determination of the self-inductance of a metal ring. Phys. Educ. 21, 1986, pp. 111-115