Levitación magnética. Inductrack

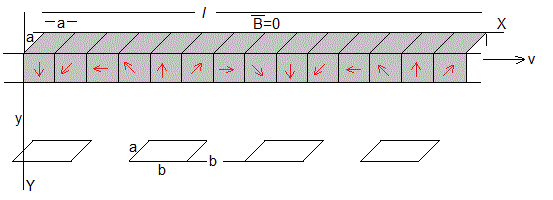
El vehículo en su parte inferior, dispone de dos hileras de imanes permanentes de forma cúbica de a=5 cm de lado. El momento magnético de dos imanes contiguos forma un ángulo de 45° tal como se muestra en la figura. El resultado es que el campo magnético por encima de la hilera es casi nulo y por debajo tiene la forma

$\vec{B} = {\begin{cases} B_{x} = B_{0} e^{- k y} \sin (k x) \\ B_{y} = B_{0} e^{- k y} \cos (k x) \end{cases}$

a=5;
k=pi/(4*a);
xx=linspace(0,10*a,50);
yy=linspace(0,2*a,5);
[x,y]=meshgrid(xx,yy);
Bx=exp(-k*y).*sin(k*x);
By=exp(-k*y).*cos(k*x);
quiver(x,y, Bx,By)
grid on
xlim([-1,53])
xlabel('x')
ylabel('y')
title('Campo magnético')

Representamos el vector campo magnético mediante una flecha en varios puntos del plano XY. Por debajo del eje X, (por encima de la hilera de imanes) el campo magnético es prácticamente nulo. Su módulo disminuye exponencialmente con la distancia y

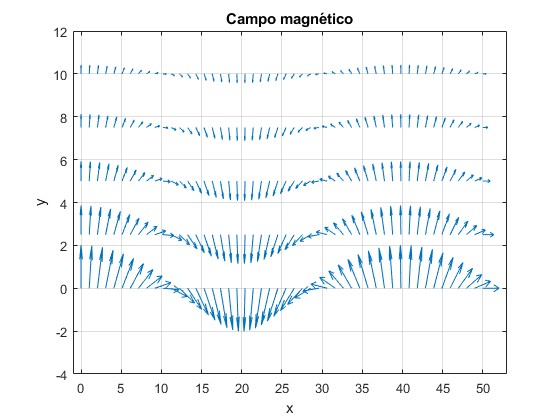
Como vemos en la primera figura, la longitud de onda es λ=8a por lo que k=2π/λ=π/(4a)= 15.7080 m^-1.

Hay dos hileras de espiras justo debajo de cada hilera de imanes. Cada espira tiene una achura a, una longitud b, estando separadas la misma distancia b cada dos espiras contiguas. Si la longitud de la hilera de imanes es l, el número de espiras que hay debajo es N=2l/(2b), el factor 2 se debe a que hay dos hileras de imanes

Corriente inducida en las espiras

Cuando el vehículo, es decir, las dos hileras de imanes permanentes se mueven con velocidad v, el campo magnético es variable con el tiempo

$\vec{B} = {\begin{cases} B_{x} = B_{0} e^{- k y} \sin (k (x - v t)) \\ B_{y} = B_{0} e^{- k y} \cos (k (x - v t)) \end{cases}$

Esta expresión, nos recuerda la propagación de un pulso a lo largo del eje X, hacia la derecha, con velocidad v o un movimiento ondulatorio armónico

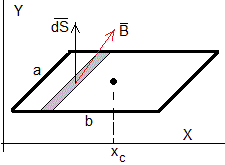
El flujo del campo magnético a través de una de las espiras cuando están a una altura y sobre la hilera de imanes, es

$\begin{array}{l} Φ = \int_{S} \vec{B} \cdot \vec{d S} = \int_{S} (B_{x} \hat{i} + B_{y} \hat{j}) \cdot (a \cdot d x \cdot \hat{j}) = a \int_{x_{c} - b / 2}^{x_{c} + b / 2} B_{y} \cdot d x = \\ B_{0} e^{- k y} \frac{a}{k} {\sin (k (x_{c} - v t) + k \frac{b}{2}) - \sin (k (x_{c} - v t) - k \frac{b}{2})} = \\ \frac{2 B_{0} a}{k} e^{- k y} \sin (k \frac{b}{2}) \cos (k (x_{c} - v t)) \end{array}$

De acuerdo con la ley de Faraday, la fem es

$\begin{array}{l} V_{ε} = - \frac{d Φ}{d t} = 2 B_{0} a v e^{- k y} \sin (k \frac{b}{2}) \sin (ω t - k x_{c}), ω = k v = \frac{π v}{4 a} \\ V_{ε} = V_{0} \sin (ω t - k x_{c}), V_{0} = 2 B_{0} a v \exp (- k y) \sin (k \frac{b}{2}) \end{array}$

V₀ es la amplitud de la fem alterna

Circuito de corriente alterna

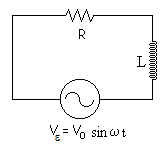
El circuito está formado por una fem, una resistencia y una autoinducción. La ecuación del circuito es

$\begin{array}{l} V_{ε} = i R + L \frac{d i}{d t} \\ V_{0} \sin (ω t - k x_{c}) = i R + L \frac{d i}{d t} \end{array}$

Se trata de un circuito similar al circuito LCR en serie, pero carece de condensador

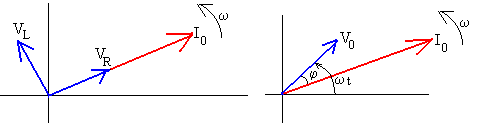
La amplitud de la intensidad i₀ y su diferencia de fase φ con la fem, son

$\begin{array}{l} i_{0} = \frac{V_{0}}{\sqrt{R^{2} + ω^{2} L^{2}}} = \frac{2 B_{0} a v \exp (- k y)}{\sqrt{R^{2} + {(k v L)}^{2}}} \sin (k \frac{b}{2}) \\ \tan φ = \frac{ω L}{R} = \frac{k v L}{R} \end{array}$

La intensidad va retrasada respecto de la fem un ángulo φ

Fuerzas sobre la espira

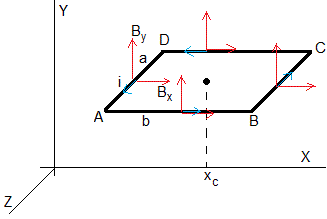
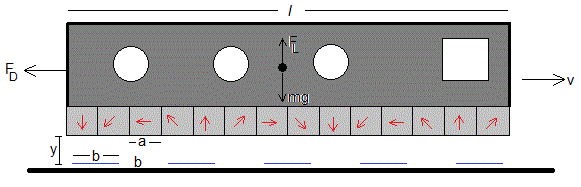
El campo magnético ejerce una fuerza sobre la corriente inducida en la espira

En la figura, se representa las componentes B_x y B_y del campo magnético (flechas de color rojo) y el sentido de la corriente inducida (contrario a las agujas del reloj, flecha en color azul)

La fuerza que ejerce el campo magnético sobre una porción de corriente rectilínea es el producto vectorial

$\vec{F} = i ({\hat{u}}_{t} \times \vec{B}) l$

Calculamos las fuerzas que ejercen cada una de las dos componentes del campo magnético, sobre cada lado de la espira

Lado AB

La componente B_x no ejerce fuerza sobre este lado de la espira

$F_{z} = i \int_{x_{c} - b / 2}^{x_{c} + b / 2} B_{y} (x) d x$

Lado BC

$\begin{array}{l} F_{x} = i a B_{y} (x_{c} + \frac{b}{2}) \\ F_{y} = - i a B_{x} (x_{c} + \frac{b}{2}) \end{array}$

Lado CD

La componente B_x no ejerce fuerza sobre este lado de la espira

$F_{z} = - i \int_{x_{c} - b / 2}^{x_{c} + b / 2} B_{y} (x) d x$

Lado DA

$\begin{array}{l} F_{x} = - i a B_{y} (x_{c} - \frac{b}{2}) \\ F_{y} = i a B_{x} (x_{c} - \frac{b}{2}) \end{array}$

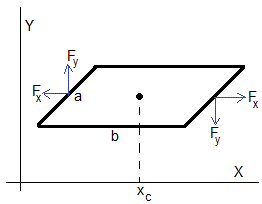
Las fuerza sobre los lados AB y CD no tienen efecto alguno sobre la espira.

Las componentes de las fuerzas sobre los lados BC y DA de la espira son

$\begin{array}{l} F_{x} = i a {B_{y} (x_{c} + \frac{b}{2}) - B_{y} (x_{c} - \frac{b}{2})} \\ F_{y} = i a {- B_{x} (x_{c} + \frac{b}{2}) + B_{x} (x_{c} - \frac{b}{2})} \end{array}$

Introduciendo las expresiones de la intensidad y de las componentes B_x y B_y del campo magnético

$\begin{array}{l} F_{x} = i_{0} \sin (ω t - k x_{c} - φ) a B_{0} e^{- k y} {\cos (k (x_{c} + \frac{b}{2}) - ω t) - \cos (k (x_{c} - \frac{b}{2}) - ω t)} \\ F_{y} = i_{0} \sin (ω t - k x_{c} - φ) a B_{0} e^{- k y} {- \sin (k (x_{c} + \frac{b}{2}) - ω t) + \sin (k (x_{c} - \frac{b}{2}) - ω t)} \end{array}$

Utilizamos las fórmulas cos(A+B)-cos(A-B)=-2sinAsinB, -sin(A+B)+ sin(A-B)=-2cosAsinB

$\begin{array}{l} {\begin{cases} F_{x} = - 2 i_{0} a B_{0} \sin (k \frac{b}{2}) e^{- k y} \sin (ω t - k x_{c} - φ) \sin (k x_{c} - ω t) \\ F_{y} = - 2 i_{0} a B_{0} \sin (k \frac{b}{2}) e^{- k y} \sin (ω t - k x_{c} - φ) \cos (k x_{c} - ω t) \end{cases} \\ {\begin{cases} F_{x} = i_{0} a B_{0} \sin (k \frac{b}{2}) e^{- k y} {\cos (- φ) - \cos (2 ω t - 2 k x_{c} - φ)} \\ F_{y} = i_{0} a B_{0} \sin (k \frac{b}{2}) e^{- k y} {\sin (2 ω t - 2 k x_{c} - φ) - \sin (- φ)} \end{cases} \end{array}$

con sin(-φ)=-sin(φ), cos(-φ)=cos(φ)

Valores medios

Se define como valor medio <f(t)> de una función periódica f(t) de periodo P a la integral

$\begin{array}{l} < f (t) > = \frac{1}{P} \int_{0}^{P} f (t) \cdot d t \\ < \sin (2 ω t + δ) > = \frac{ω}{π} \int_{0}^{π / ω} \sin (2 ω t + δ) \cdot d t = 0 \end{array}$

>> syms w t a;
>> int(sin(2*w*t+a),t,0,pi/w)*w/pi
ans =0

Valor medio de la componente F_y

$< F_{y} > = i_{0} a B_{0} \sin (k \frac{b}{2}) e^{- k y} \sin φ$

Introduciendo las expresiones de la amplitud de la intensidad i₀ y desfase φ

$\begin{array}{l} < F_{y} > = \frac{2 B_{0}^{2} a^{2} v \exp (- 2 k y)}{\sqrt{R^{2} + {(k v L)}^{2}}} \sin^{2} (k \frac{b}{2}) \frac{\frac{k v L}{R}}{\sqrt{1 + {(\frac{k v L}{R})}^{2}}} \\ = 2 B_{0}^{2} a^{2} k L \exp (- 2 k y) \frac{v^{2}}{R^{2} + {(k v L)}^{2}} \sin^{2} (k \frac{b}{2}) \end{array}$

Valor medio de la componente F_x

$< F_{x} > = i_{0} a B_{0} \sin (k \frac{b}{2}) e^{- k y} \cos φ$

Introduciendo las expresiones de la amplitud de la intensidad i₀ y desfase φ

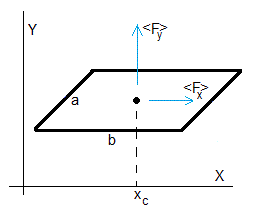
$\begin{array}{l} < F_{x} > = \frac{2 B_{0}^{2} a^{2} v \exp (- 2 k y)}{\sqrt{R^{2} + {(k v L)}^{2}}} \sin^{2} (k \frac{b}{2}) \frac{1}{\sqrt{1 + {(\frac{k v L}{R})}^{2}}} = \\ 2 B_{0}^{2} a^{2} R \exp (- 2 k y) \frac{v}{R^{2} + {(k v L)}^{2}} \sin^{2} (k \frac{b}{2}) \end{array}$

Representamos cualitativamente las componentes de la fuerza F_x y F_y que ejerce el campo magnético de la hilera de imanes sobre la espira

hold on
Fx=@(v) v./(1+v.^2);
Fy=@(v) (v.^2)./(1+v.^2);
fplot(Fx,[0,10])
fplot(Fy,[0,10])
hold off
grid on
xlabel('x')
legend('F_x', 'F_y', 'location', 'best')
ylabel('y')
title('Componentes de la fuerza sobre la espira')

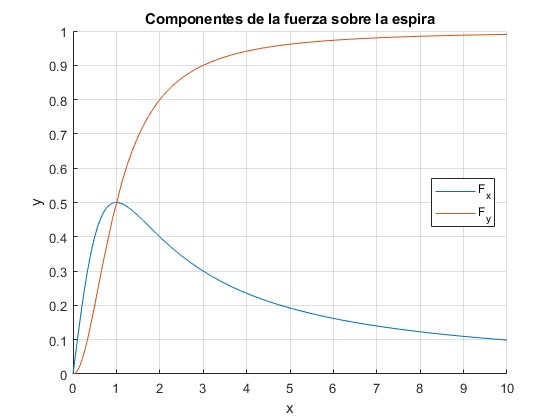
La componente <F_y> tiende hacia un valor límite a medida que la velocidad se incrementa

La componente <F_x> alcanza un valor máximo para cierta velocidad v_m.

$\begin{array}{l} \frac{d F_{x}}{d v} = \frac{R^{2} + {(k v L)}^{2} - v \cdot 2 k^{2} L^{2} v}{{(R^{2} + {(k v L)}^{2})}^{2}} = 0 \\ v_{m} = \frac{R}{k L} \end{array}$

Fuerzas sobre el vehículo

La fuerza repulsiva <F_y> que ejerce el campo magnético sobre la espira tiende a alejar la espira de los imanes. Por la tercera ley de Newton, la espira que está fija en el raíl, ejerce una fuerza igual y de sentido contrario sobre los imanes. Ejerce una fuerza de empuje contraria al peso sobre el vehículo

Por la tercera ley de Newton, la fuerza <F_x> frena al vehículo, como corresponde a una corriente inducida

<F_x> y <F_y> son las fuerzas que ejerce una espira sobre el vehículo, pero hay, N=l/b, espiras debajo de las dos hileras de imanes. Las fuerzas netas son

Fuerza de empuje

$F_{L} = \frac{2 B_{0}^{2} a^{2} k L l \exp (- 2 k y)}{b} \frac{v^{2}}{R^{2} + {(k v L)}^{2}} \sin^{2} (k \frac{b}{2})$

Llamando x=b/a y teniendo en cuenta que k=π/(4 a)

$\begin{array}{l} F_{L} = \frac{π B_{0}^{2} L l \exp (- 2 k y)}{2 x} \frac{v^{2}}{R^{2} + {(k v L)}^{2}} \sin^{2} (\frac{π}{8} x) \\ F_{L} = F_{0} \frac{\sin^{2} (\frac{π}{8} x)}{x} \end{array}$

Derivando e igualando a cero

$\begin{array}{l} \frac{π}{4} \sin (\frac{π}{8} x) \cos (\frac{π}{8} x) x - \sin^{2} (\frac{π}{8} x) = 0 \\ \tan (\frac{π}{8} x) = \frac{π}{4} x \end{array}$

La solución de esta ecuación transcendente es b/a=2.9681

f=@(x) sin(pi*x/8).^2./x;
fplot(f,[0,10])
g=@(x) tan(pi*x/8)-pi*x/4;
x0=fzero(g,3);
line([x0,x0],[0,f(x0)],'lineStyle','--')
grid on
xlabel('x')
ylabel('f(x)')
title('b/a óptimo')

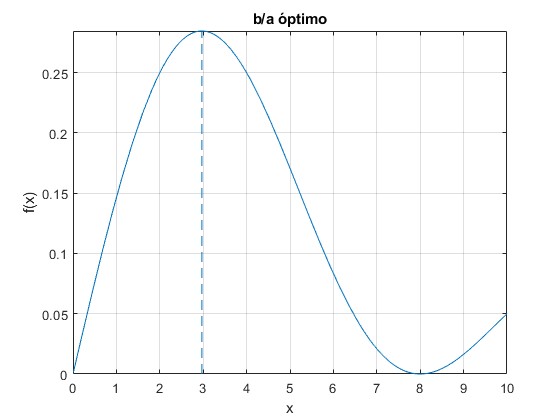
La fuerza de empuje para este valor óptimo de b/a es

$F_{L} = 0.447 B_{0}^{2} L l \exp (- 2 k y) \frac{v^{2}}{R^{2} + {(k v L)}^{2}}$

Para y=0, el vehículo queda suspendido cuando F_l=mg, cuando su velocidad v_t es de

$\begin{array}{l} m g = 0.447 B_{0}^{2} L l \frac{v^{2}}{R^{2} + {(k v L)}^{2}} \\ v_{t} = R \sqrt{\frac{m g}{0.447 B_{0}^{2} L l - m g {(k L)}^{2}}} \end{array}$

Con los datos:

Longitud de la hilera de imanes, l=10 m
Masa del vehículo, m=10 000 kg
Coeficiente de autoinducción de cada espira, L=1.0·10^-7 H
Resistencia de la espira, R=1.0·10^-5 Ω
Amplitud del campo magnético, B₀=1.4 T

El resultado es v_t=3.9299 m/s (14.1 km/h)

Para velocidades mayores v>v_t, el vehículo queda suspendido a una altura y por encima de los raíles tal que

$\begin{array}{l} m g = 0.447 B_{0}^{2} L l \exp (- 2 k y) \frac{v^{2}}{R^{2} + {(k v L)}^{2}} \\ y = \frac{1}{2 k} \ln (\frac{0.447 B_{0}^{2} v^{2} L l}{m g (R^{2} + {(k v L)}^{2})}) \end{array}$

para v=360 km/h (100 m/s), y=0.0409 m=4.1 cm

Fuerza de frenado

$F_{D} = \frac{2 B_{0}^{2} a^{2} R \exp (- 2 k y)}{b} \frac{v}{R^{2} + {(k v L)}^{2}} \sin^{2} (k \frac{b}{2})$

Referencias

WoPhO Problems and Solutions. 2011, Indonesia. Maglev trains levitation