Consideremos el siguiente circuito formado por un condensador de capacidad C, una resistencia R, una autoinducción L y una batería de fem V₀ sin resistencia interna.

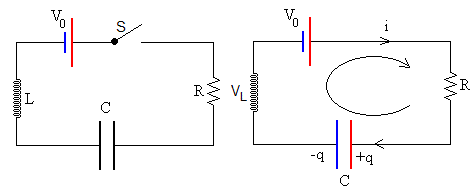
El condensador está inicialmente descargado. En el instante t=0, se cierra el circuito. En un instante dado t, tendremos que

• El condensador C tiene una carga q
• Por la resistencia R circula una corriente de intensidad i.
• Por la autoinducción L circula una corriente de intensidad i.

La ecuación del circuito es

${\displaystyle \begin{array}{l}{V}_L+V_0-\frac{q}{C}=iR\\ \left(-L\frac{di}{dt}\right)+V_0-\frac{q}{C}=iR,i=\frac{dq}{dt}\end{array}}$

La corriente i añade carga de la placa positiva, por lo que i=dq/dt

${\displaystyle \begin{array}{l}\frac{d^{2}q}{d{t}^2}+\frac{R}{L}\frac{dq}{dt}+\frac{1}{LC}q=\frac{V_0}{L}\\ \frac{d^{2}q}{d{t}^2}+2\gamma \frac{dq}{dt}+{\omega }_0^{2}q=\frac{V_0}{L}\end{array}}$

La solución de esta ecuación diferencial es de la forma

${\displaystyle q=y_1+\exp (-\gamma t)(A·\sin \omega t+B·\cos \omega t){\omega }^2={\omega }_0^2-{\gamma }^2}$

La primera y₁ una constante, es la solución particular. El segundo término es la solución de la ecuación diferencial homogénea que ya encontramos en el estudio de las oscilaciones amortiguadas γ<ω₀.

Introduciendo la solución particular y₁ en la ecuación diferencial tenemos que

y₁=CV₀

Inicialmente el condensador C está descargado q=0 y la intensidad i=dq/dt es cero.

Las condiciones iniciales q=0, y dq/dt=0 determinan las constantes A y B. Después de hacer algunas operaciones tenemos que

${\displaystyle \begin{array}{l}q=C{V}_0\left(1-\exp (-\gamma t)\left(\frac{\gamma }{\omega }\sin \omega t+\cos \omega t\right)\right)\\ i=\frac{dq}{dt}=\frac{V_0}{L\omega }\exp (-\gamma t)\sin \omega t\end{array}}$

Comprobamos que en el instante t=0, q=0 e i=0, y que para t→∞,

${\displaystyle q\to C{V}_0}$

Diferencia de potencial en los extremos de cada uno de los elementos del circuito

• En la batería el potencial del polo negativo a es menor que el polo positivo b, de modo que

V_ab=-V₀

• En la resistencia R la corriente de intensidad i circula de b a c, luego

${\displaystyle V_{bc}=iR=V_0\frac{2\gamma }{\omega }\exp (-\gamma t)\sin (\omega t)}$

• En el condensador C el potencial de c (placa positiva) es mayor que el a (placa negativa), de modo que

${\displaystyle V_{cd}=\frac{q}{C}=V_0\left(1-\exp (-\gamma t)\left(\frac{\gamma }{\omega }\text{sin(}\omega t)+\cos (\omega t)\right)\right)}$

• En la autoinducción es equivalente a una batería que se está cargando, ya que se opone a que aumente la intensidad. La diferencia de potencial entre d y a es.

${\displaystyle V_{da}=L\frac{di}{dt}=V_0\exp (-\gamma t)\left(\text{cos(}\omega t)\text{-}\frac{\gamma }{\omega }\text{sin(}\omega t)\right)}$

Sea el circuito LCR

• Condensador, C=9.66·10^-9 F
• Resistencia, R=1044 Ω
• Autoinducción, L=9.44 H
• Batería, V₀=4.04 V

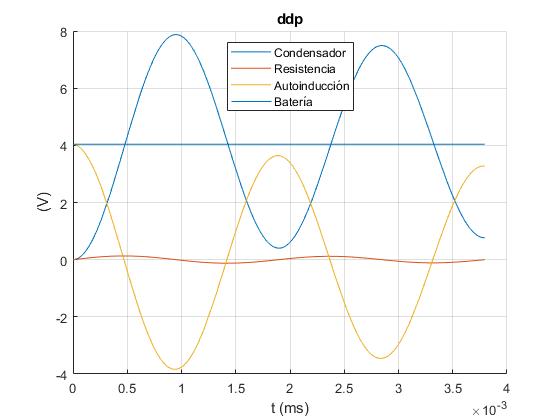
Representamos la diferencia de potencial en los extremos de cada uno de los elementos del circuito durante las dos primeras oscilaciones. El periodo de una oscilación es 2π/ω

R=1044; %resistencia
C=9.66e-9; %condensador
L=9.44; %autoinducción
V0=4.04; %batería

w0=sqrt(1/(L*C)); %frecuencia propia
w=sqrt(w0^2-gamma^2); %frecuencia
hold on
f=@(t) V0*(1-exp(-gamma*t).*(gamma*sin(w*t)/w+cos(w*t))); %condensador
fplot(f,[0,2*2*pi/w])
f=@(t) V0*2*gamma*exp(-gamma*t).*sin(w*t)/w; %resistencia
fplot(f,[0,2*2*pi/w])
f=@(t) V0*exp(-gamma*t).*(cos(w*t)-gamma*sin(w*t)/w); %autoinducción
fplot(f,[0,2*2*pi/w])
line([0,2*2*pi/w],[V0,V0]) %batería
hold off
legend('Condensador','Resistencia','Autoinducción','Batería','location','north')
xlabel('t (ms)')
ylabel('(V)')
grid on
title('ddp')

Estudio energético

• La energía almacenada en el condensador en forma de campo eléctrico es

${\displaystyle U_C=\frac{1}{2}\frac{q^2}{C}=\frac{1}{2}C{V}_0^2{\left(1-\exp (-\gamma t)\left(\frac{\gamma }{\omega }\sin (\omega t)+\cos (\omega t)\right)\right)}^2}$

• La energía almacenada en la autoinducción en forma de campo magnético es

${\displaystyle U_L=\frac{1}{2}L{i}^2=\frac{1}{2}\frac{V_0^2}{L{\omega }^2}\exp (-2\gamma t){\sin }^{\text{2}}(\omega t)}$

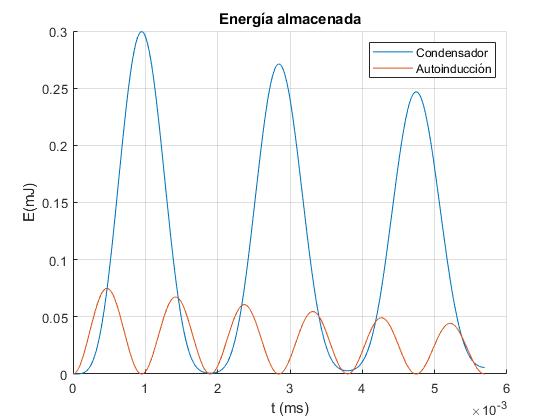
Representamos la energía almacenda en mJ (·10^-6 J) en el condensador y en la autoinducción en las tres primeras oscilaciones.

R=1044; %resistencia
C=9.66e-9; %condensador
L=9.44; %autoinducción
V0=4.04; %batería

w0=sqrt(1/(L*C)); %frecuencia propia
w=sqrt(w0^2-gamma^2); %frecuencia
hold on
%condensador
f=@(t) C*V0^2*(1-exp(-gamma*t).*(gamma*sin(w*t)/w+cos(w*t))).^2*1e6/2; 
fplot(f,[0,3*2*pi/w])
%autoinducción
f=@(t) V0^2*exp(-2*gamma*t).*(sin(w*t).^2)*1e6/(2*L*w^2); 
fplot(f,[0,3*2*pi/w])
legend('Condensador','Autoinducción')
xlabel('t (ms)')
ylabel('E(mJ)')
grid on
title('Energía almacenada')



• La energía disipada en la resistencia es

$$\begin{gathered} {\displaystyle \begin{array}{l}{U}_R={\displaystyle \underset{0}{\overset{t}{\int }}{i}^{2}R·dt=\frac{R{V}_0^2}{L^2{\omega }^2}{\displaystyle \underset{0}{\overset{t}{\int }}\exp (-2\gamma t){\text{sin}}^{\text{2}}(\omega t)dt}}= \\ \frac{R{V}_0^2}{2L^2{\omega }^2}{\displaystyle \underset{0}{\overset{t}{\int }}\exp (-2\gamma t)(1-\cos (2\omega t))dt}=\\ \frac{R{V}_0^2}{4L^2{\omega }^2}\left\{\frac{1}{\gamma }\left(1-\exp (-2\gamma t)\right)-\frac{1}{{\omega }_0^2}\left(\exp (-2\gamma t)(\omega ·\sin (2\omega t)-\gamma \cos (2\omega t))+\gamma \right)\right\}\end{array}} \end{gathered}$$

Se integra por partes, para llegar a la expresión final se tiene en cuenta que ${\omega }^2={\omega }_0^2-{\gamma }^2$

• La energía suministrada por la batería es

${\displaystyle \begin{array}{l}{U}_V={\displaystyle \underset{0}{\overset{t}{\int }}{V}_{0}i·dt}=\frac{V_0^2}{L\omega }{\displaystyle \underset{0}{\overset{t}{\int }}\exp (-\gamma t)\sin (\omega t)·dt}=\\ V_0^{2}C\left(1-\exp (-\gamma t)(\cos (\omega t)+\frac{\gamma }{\omega }\sin (\omega t)\right)\end{array}}$

Se comprueba la conservación de la energía

U_V=U_C+U_L+U_R

R=1044; %resistencia
C=9.66e-9; %condensador
L=9.44; %autoinducción
V0=4.04; %batería

gamma=R/(2*L); %amortiguamiento
w0=sqrt(1/(L*C)); %frecuencia propia
w=sqrt(w0^2-gamma^2); %frecuencia
hold on
%condensador
f1=@(t) C*V0^2*(1-exp(-gamma*t).*(gamma*sin(w*t)/w+cos(w*t))).^2*1e6/2; 
%auotoinducción
f2=@(t) V0^2*exp(-2*gamma*t).*(sin(w*t).^2)*1e6/(2*L*w^2); 
%resistencia
f3=@(t) R*V0^2*((1-exp(-2*gamma*t))/gamma-(exp(-2*gamma*t).*(w*sin(2*w*t)-
gamma*cos(2*w*t))+gamma)/w0^2)*1e6/(4*L^2*w^2);
%suma: condensador+autoinducción+resistencia
f=@(t) f1(t)+f2(t)+f3(t); 
fplot(f,[0,3*2*pi/w])
%batería
f4=@(t) V0^2*C*(1-exp(-gamma*t).*(cos(w*t)+gamma*sin(w*t)/w))*1e6;
fplot(f4,[0,3*2*pi/w])

xlabel('t (ms)')
ylabel('E(mJ)')
grid on
title('Conservación de la energía')

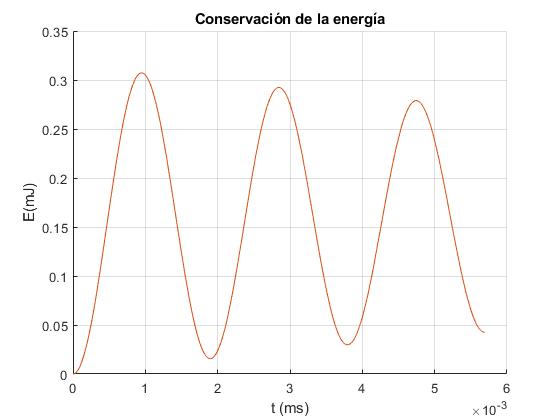
Coinciden las dos funciones f(t) y f4(t) en el intervalo especificado

Una parte de la energía suministrada por la batería, se almacena en el condensador, otra parte en la autoinducción y el resto se disipa en la resistencia.

Después de un tiempo t→∞

• La carga en el condensador tiende a CV_0, la energía almacenada en el condensador es

${\displaystyle U_C=\frac{1}{2}C{V}_0^2}$

• La intensidad tiende a cero, no hay energía almacenada en la autoinducción

U_L=0

• La energía disipada en la resistencia tiende a

${\displaystyle U_R=\frac{R{V}_0^2}{4L^2{\omega }^2}\left\{\frac{1}{\gamma }-\frac{\gamma }{{\omega }_0^2}\right\}=\frac{R{V}_0^2}{4L^2{\omega }^2}\frac{{\omega }^2}{\gamma {\omega }_0^2}=\frac{1}{2}C{V}_0^2}$

• La energía suministrada por la batería tiende a

U_V=CV₀

La mitad de la energía suministrada por la batería se almacena como energía del campo eléctrico en el condensador y la otra mitad se disipa en la resistencia. El mismo resultado obtenido en la carga del condensador sin autoinducción

Derivada de la energía respecto del tiempo

La derivada de la energía de un elemento del circuito con respecto del tiempo t, nos proporciona la siguiente información: Si la derivada es positiva, indica que ese elemento está proporcionando energía al circuito, si es negativa indica que está disipando o almacenando energía

${\displaystyle \begin{array}{l}\frac{d{U}_V}{dt}-\frac{d{U}_C}{dt}-\frac{d{U}_L}{dt}-\frac{d{U}_R}{dt}=0\\ \frac{d{U}_C}{dt}=\frac{V_0^2}{L\omega }\exp (-\gamma t)\sin (\omega t)\left(1-\exp (-\gamma t)\left(\frac{\gamma }{\omega }\sin (\omega t)+\cos (\omega t)\right)\right)\\ \frac{d{U}_L}{dt}=\frac{V_0^2}{L\omega }\exp (-2\gamma t)\sin (\omega t)\left(\cos (\omega t)-\frac{\gamma }{\omega }\sin (\omega t)\right)\\ \frac{d{U}_R}{dt}=\frac{2\gamma V_0^2}{L{\omega }^2}\exp (-2\gamma t){\sin }^2(\omega t)\\ \frac{d{U}_V}{dt}=\frac{V_0^2}{L\omega }\exp (-\gamma t)\sin (\omega t)\end{array}}$

Respresentamos la derivada de la energía de cada elemento del circuito respecto del tiempo en (mW) en función del tiempo t en el primer periodo de oscilación

R=1044; %resistencia
C=9.66e-9; %condensador
L=9.44; %autoinducción
V0=4.04; %batería

gamma=R/(2*L); %amortiguamiento
w0=sqrt(1/(L*C)); %frecuencia propia
w=sqrt(w0^2-gamma^2); %frecuencia
hold on
%condensador
f=@(t) -V0^2*exp(-gamma*t).*sin(w*t).*(1-exp(-gamma*t).*(gamma*sin(w*t)/w+cos(w*t)))
*1e6/(L*w);
fplot(f,[0,2*pi/w])
%autoinducción
f=@(t) -V0^2*exp(-2*gamma*t).*sin(w*t).*(cos(w*t)-gamma*sin(w*t)/w)*1e6/(L*w);
fplot(f,[0,2*pi/w])
%resistencia
f=@(t) -2*gamma*V0^2*exp(-2*gamma*t).*(sin(w*t).^2)*1e6/(L*w^2);
fplot(f,[0,2*pi/w])
%batería
f=@(t) V0^2*exp(-gamma*t).*sin(w*t)*1e6/(L*w);
fplot(f,[0,2*pi/w])

legend('Condensador','Autoinducción', 'Resistencia','Batería')
xlabel('t (ms)')
ylabel('dE/dt (mW)')
grid on
title('Derivada de la energía')

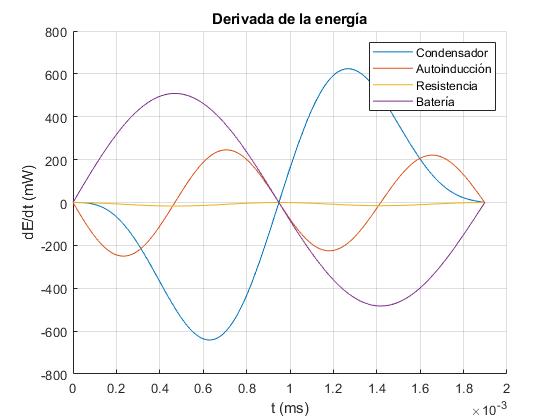
Poco después de cerrar el circuito, la resistencia disipa energía, el condensador y la autoinducción almacenan energía (pendiente negativa). La batería proporciona energía (pendiente positiva)

Actividades

Se introduce

• El coeficiente de autoinducción L en H, en el control titulado Autoinducción

• La capacidad del condensador C en nF (10^-9), en el control titulado Capacidad.

• La resistencia R en kΩ (10³), en el control titulado Resistencia.

• La fem de la batería se ha fijado en V₀=4 V

Se pulsa el botón titulado Nuevo

Se representa, la diferencia de potencial en los extremos de

• La batería (se toma como valor positivo)
• En el condensador
• En la autoinducción
• En la resistencia

Observamos el estado transitorio y su evolución hacia el estado estacionario, cuando t→∞

Si aumentamos la resistencia, se tarda menos tiempo en alcanzar aproximadamente el estado estacionario.

El circuito estudiado en el artículo citado en las referencias consta de

• Una resistencia, R=1.044·10³ Ω
• Un condensador, C=9.66·10^-9 F
• Autoinducción, L=9.44 H
• Batería, V₀=4.04 V

La frecuencia del circuito vale

${\displaystyle {\omega }^2={\omega }_0^2-{\gamma }^2=\frac{1}{LC}-\frac{R^2}{4L^2}}$

ω₀=3311.5 rad/s
γ=55.3 s^-1

Estamos en la situación descrita en esta página (amortiguada) γ< ω₀

Referencias

Faleski M. C. Transient behaviour of the driven RLC circuit. Am . J. Phys. 74 (5) May 2006, pp. 429-437