Osciladores LC acoplados inductivamente

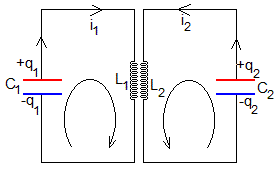
En la figura, se muestran dos circuitos LC. Las bobinas están acopladas magnéticamente, de forma similar a un transformador. Por circuito izquierdo, circula una corriente i₁ que varía con el tiempo. En el circuito derecho, se genera una fem V_M2=-M·di₁/dt. Siendo M el coeficiente de inducción mutua. Del mismo modo, por el circuito derecho circula una corriente i₂ que varía con el tiempo. En el izquierdo, se genera una fem V_M1=-M·di₂/dt

Las ecuaciones de los dos circuitos acoplados son

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{q_1}{C_1}+\left(-L_1\frac{d{i}_1}{dt}\right)+\left(-M\frac{d{i}_2}{dt}\right)=0\\ \frac{q_2}{C_2}+\left(-L_2\frac{d{i}_2}{dt}\right)+\left(-M\frac{d{i}_1}{dt}\right)=0\end{array}\\ i_1=-\frac{d{q}_1}{dt},i_2=-\frac{d{q}_2}{dt}\end{array}}$

En ambos casos, las corrientes extraen cargas de la placa positiva de los dos condensadores por lo que i=-dq/dt

Tenemos que resolver un sistema de dos ecuaciones diferenciales

${\displaystyle \begin{array}{l}\frac{d^2{q}_1}{d{t}^2}+m_1\frac{d^2{q}_2}{d{t}^2}+{\omega }_{10}^2{q}_1=0\\ \frac{d^2{q}_2}{d{t}^2}+m_2\frac{d^2{q}_1}{d{t}^2}+{\omega }_{20}^2{q}_2=0\end{array}\}\{\begin{array}{l}{\omega }_{10}^2=\frac{1}{L_1{C}_1},{\omega }_{20}^2=\frac{1}{L_2{C}_2}\\ m_1=\frac{M}{L_1},m_2=\frac{M}{L_2}\end{array}}$

Ensayamos una solución de la forma, q₁=Q₁sin(ωt+φ) y q₂=Q₂sin(ωt+φ)

Obtenemos un sistema homogéneo de dos ecuaciones con dos incógnitas

${\displaystyle \begin{array}{l}\{\begin{array}{l}-{\omega }^2{Q}_1-m_1{\omega }^2{Q}_2+{\omega }_{10}^2{Q}_1=0\\ -{\omega }^2{Q}_2-m_2{\omega }^2{Q}_1+{\omega }_{20}^2{Q}_2=0\end{array}\\ \left(\begin{array}{cc}{\omega }_{10}^2-{\omega }^2& -m_1{\omega }^2\\ -m_2{\omega }^2& {\omega }_{20}^2-{\omega }^2\end{array}\right)\left(\begin{array}{c}{Q}_1\\ Q_2\end{array}\right)=0\end{array}}$

El determinante de la matriz deberá ser cero

${\displaystyle \begin{array}{l}\left(1-m_1{m}_2\right){\omega }^4-\left({\omega }_{10}^2+{\omega }_{20}^2\right){\omega }^2+{\omega }_{10}^2{\omega }_{20}^2=0\\ {\omega }_{\mathrm{1,2}}^2=\frac{{\omega }_{10}^2+{\omega }_{20}^2\pm \sqrt{{\left({\omega }_{10}^2-{\omega }_{20}^2\right)}^2+4m_1{m}_2{\omega }_{10}^2{\omega }_{20}^2}}{2\left(1-m_1{m}_2\right)}\end{array}}$

Para cada una de las frecuencias ω₁ y ω₂ de los dos modos normales de vibración, los coeficientes Q₁ y Q₂ están relacionados, tomamos una de las dos ecuaciones, por ejemplo, la primera.

${\displaystyle \begin{array}{l}{r}_1=\frac{Q_2^{(1)}}{Q_1^{(1)}}=\frac{{\omega }_{10}^2-{\omega }_1^2}{m_1{\omega }_1^2}\\ r_2=\frac{Q_2^{(2)}}{Q_1^{(2)}}=\frac{{\omega }_{10}^2-{\omega }_2^2}{m_1{\omega }_2^2}\end{array}}$

La carga de cada uno de los dos condensadores q₁ y q₂ es la combinación lineal de los dos modos normales de vibración de frecuencias angulares ω₁ y ω₂

${\displaystyle \{\begin{array}{l}{q}_1=Q_1^{(1)}\sin ({\omega }_{1}t+{\phi }_1)+Q_1^{(2)}\sin ({\omega }_{2}t+{\phi }_2)\\ q_2=Q_2^{(1)}\sin ({\omega }_{1}t+{\phi }_1)+Q_2^{(2)}\sin ({\omega }_{2}t+{\phi }_2)=\\ r_1{Q}_1^{(1)}\sin ({\omega }_{1}t+{\phi }_1)+r_2{Q}_1^{(2)}\sin ({\omega }_{2}t+{\phi }_2)\end{array}}$

Las intensidades i son las derivadas de las cargas q respecto del tiempo t

${\displaystyle \{\begin{array}{l}{i}_1=Q_1^{(1)}{\omega }_1\cos ({\omega }_{1}t+{\phi }_1)+Q_1^{(2)}{\omega }_2\cos ({\omega }_{2}t+{\phi }_2)\\ i_2=r_1{Q}_1^{(1)}{\omega }_1\cos ({\omega }_{1}t+{\phi }_1)+r_2{Q}_1^{(2)}{\omega }_2\cos ({\omega }_{2}t+{\phi }_2)\end{array}}$

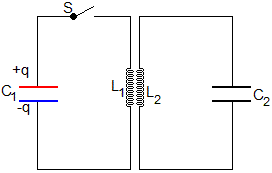
Fijamos unas condiciones iniciales sencillas, por ejemplo, el primer condensador de capacidad C₁ está cargado con carga q, el segundo, de capacidad C₂ está descargado. Las corrientes iniciales i₁=0 e i₂=0, son nulas

${\displaystyle t=\mathrm{0,}\{\begin{array}{l}{q}_1=q\\ q_2=0\end{array}\{\begin{array}{l}{i}_1=0\\ i_2=0\end{array}}$

Las condiciones iniciales determinan los dos coeficientes Q y las dos fases φ

${\displaystyle \begin{array}{l}\{\begin{array}{l}q=Q_1^{(1)}\sin {\phi }_1+Q_1^{(2)}\sin {\phi }_2\\ 0=r_1{Q}_1^{(1)}\sin {\phi }_1+r_2{Q}_1^{(2)}\sin {\phi }_2\end{array}\\ \{\begin{array}{l}0={\omega }_1{Q}_1^{(1)}\cos {\phi }_1+{\omega }_2{Q}_1^{(2)}\cos {\phi }_2\\ 0={\omega }_1{r}_1{Q}_1^{(1)}\cos {\phi }_1+{\omega }_2{r}_2{Q}_1^{(2)}\cos {\phi }_2\end{array}\end{array}}$

Las dos últimas ecuaciones implican que las fases φ₁=π/2 y φ₂=π/2

De las dos primeras ecuaciones, se obtiene

${\displaystyle \begin{array}{l}\{\begin{array}{l}q=Q_1^{(1)}+Q_1^{(2)}\\ 0=r_1{Q}_1^{(1)}+r_2{Q}_1^{(2)}\end{array}\\ Q_1^{(1)}=-\frac{r_2}{r_1-r_2}q,Q_1^{(2)}=\frac{r_1}{r_1-r_2}q\end{array}}$

La carga q de cada condensador en función del tiempo t es

${\displaystyle \{\begin{array}{l}{q}_1=-\frac{r_2}{r_1-r_2}q\sin \left({\omega }_{1}t+\frac{\pi }{2}\right)+\frac{r_1}{r_1-r_2}q\sin \left({\omega }_{2}t+\frac{\pi }{2}\right)=\\ -\frac{r_2}{r_1-r_2}q\cos \left({\omega }_{1}t\right)+\frac{r_1}{r_1-r_2}q\cos \left({\omega }_{2}t\right)\\ q_2=\frac{r_1{r}_2}{r_1-r_2}q\left(-\cos \left({\omega }_{1}t\right)+\cos \left({\omega }_{2}t\right)\right)\end{array}}$

Caso particular

Cuando los osciladores son iguales, L₁=L₂=L, C₁=C₂=C, se cumple ω₁₀=ω₂₀=ω₀, m₁=m₂=m

Las frecuencias de los modos normales de vibración son

${\displaystyle {\omega }_{\mathrm{1,2}}^2=\frac{{\omega }_0^2\left(1\pm m\right)}{1-m^2},\{\begin{array}{l}{\omega }_1^2=\frac{{\omega }_0^2}{1-m}\\ {\omega }_2^2=\frac{{\omega }_0^2}{1+m}\end{array}}$

Los coeficientes r

${\displaystyle \begin{array}{l}{r}_1=\frac{Q_2^{(1)}}{Q_1^{(1)}}=-1\\ r_2=\frac{Q_2^{(2)}}{Q_1^{(2)}}=1\end{array}}$

La carga q de cada condensador en función del tiempo t es

${\displaystyle \{\begin{array}{l}{q}_1=\frac{1}{2}q\left(\cos \left({\omega }_{1}t\right)+\cos \left({\omega }_{2}t\right)\right)=q\cos \left(\frac{{\omega }_1+{\omega }_2}{2}t\right)\cos \left(\frac{{\omega }_1-{\omega }_2}{2}t\right)\\ q_2=\frac{1}{2}q\left(-\cos \left({\omega }_{1}t\right)+\cos \left({\omega }_{2}t\right)\right)=q\sin \left(\frac{{\omega }_1+{\omega }_2}{2}t\right)\sin \left(\frac{{\omega }_1-{\omega }_2}{2}t\right)\end{array}}$

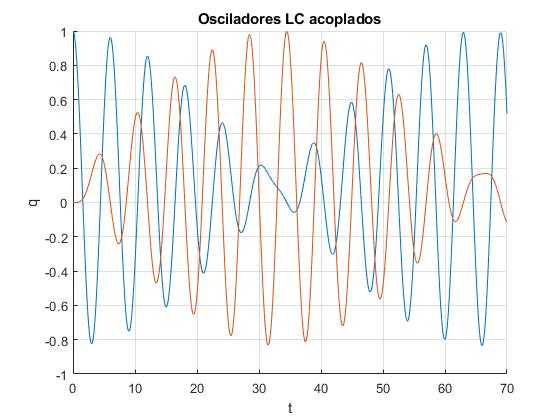
Representamos q₁ y q₂ en función del tiempo t. Tomamos q=1, ω₀=1, y m=0.1. Las frecuencias de los modos normales de vibración son próximas ω₁= 1.0541 y ω₂= 0.9535 si el acoplamiento m es pequeño

w0=1;
m=0.1;
%frecuencias de los modos normales de vibración
w1=w0/sqrt(1-m);
w2=w0/sqrt(1+m);
hold on
fplot(@(t) cos((w1+w2)*t/2).*cos((w1-w2)*t/2),[0,70])
fplot(@(t) sin((w1+w2)*t/2).*sin((w1-w2)*t/2),[0,70])
hold off
grid on
xlabel('t')
ylabel('q')
legend('q_1','q_2','Location','best')
title('Osciladores LC acoplados')

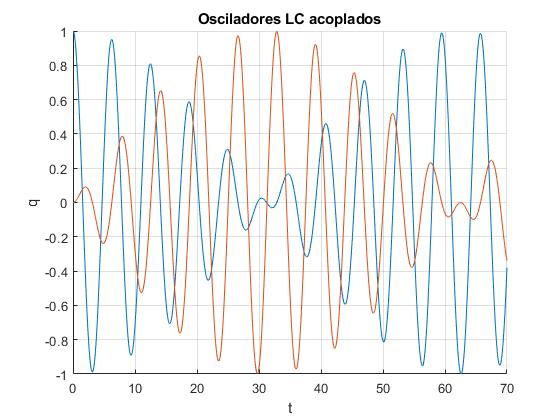
Obtenemos pulsos, un comportamiento similar al de los osciladores acoplados descritos en la página titulada Dos osciladores acoplados bajo la acción de una fuerza oscilante

Osciladores LC acoplados mediante un condensador

Sean dos circuitos LC acoplados por un condensador C₃. En el instante t=0, el condensador C₁ está cargado con una carga q y los otros descargados, las intensidades son nulas.

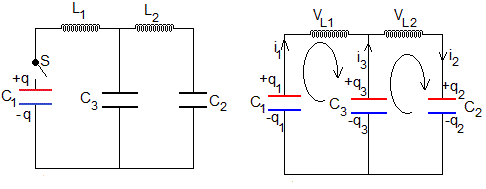
Las ecuaciones del circuito son

${\displaystyle \begin{array}{l}\{\begin{array}{l}{V}_{L1}-\frac{q_3}{C_3}+\frac{q_1}{C_1}=0\\ V_{L2}-\frac{q_2}{C_2}+\frac{q_3}{C_3}=0\end{array}\\ \{\begin{array}{l}-L_1\frac{d{i}_1}{dt}-\frac{q_3}{C_3}+\frac{q_1}{C_1}=0\\ -L_2\frac{d{i}_2}{dt}-\frac{q_2}{C_2}+\frac{q_3}{C_3}=0\end{array}\\ i_1=-\frac{d{q}_1}{dt},i_2=\frac{d{q}_2}{dt},i_3=-\frac{d{q}_3}{dt}\\ i_1+i_3=i_2\\ q_1+q_2+q_3=q\end{array}}$

Las corrientes i₁ e i₃ extraen cargas de la placa positiva de los condensadores C₁ y C₃ por lo que i=-dq/dt. La corriente i₂ añade cargas a la placa positiva del condensador C₂. La carga inicial q se reparte entre los tres condensadores de modo que la suma es constante e igual a q

Tenemos que resolver un sistema de dos ecuaciones diferenciales

${\displaystyle \{\begin{array}{l}\frac{d^2{q}_1}{d{t}^2}+\frac{1}{L_1}\left(\frac{1}{C_1}+\frac{1}{C_3}\right)q_1+\frac{1}{L_1{C}_3}{q}_2=\frac{q}{L_1{C}_3}\\ \frac{d^2{q}_2}{d{t}^2}+\frac{1}{L_2}\left(\frac{1}{C_2}+\frac{1}{C_3}\right)q_2+\frac{1}{L_2{C}_3}{q}_1=\frac{q}{L_2{C}_3}\end{array}}$

Ensayamos una solución de la forma, q₁=x₁+Q₁sin(ωt+φ) y q₂=x₂+Q₂sin(ωt+φ). Donde x₁ y x₂ son las soluciones particulares de cada ecuación diferencial y el término armónico, es la solución de la ecuación diferencial homogénea.

Solución particular

Obtenemos las soluciones particulares, resolviendo el sistema de dos ecuaciones con dos incógnitas

${\displaystyle \{\begin{array}{l}\frac{1}{L_1}\left(\frac{1}{C_1}+\frac{1}{C_3}\right)x_1+\frac{1}{L_1{C}_3}{x}_2=\frac{q}{L_1{C}_3}\\ \frac{1}{L_2}\left(\frac{1}{C_2}+\frac{1}{C_3}\right)x_2+\frac{1}{L_2{C}_3}{x}_1=\frac{q}{L_2{C}_3}\end{array}}$

Llamamos

${\displaystyle a=\frac{1}{L_1}\left(\frac{1}{C_1}+\frac{1}{C_3}\right),b=\frac{1}{L_2}\left(\frac{1}{C_2}+\frac{1}{C_3}\right),c=\frac{1}{L_1{C}_3},d=\frac{1}{L_2{C}_3}}$

La solución del sistema de dos ecuaciones es

${\displaystyle \begin{array}{l}\{\begin{array}{l}a{x}_1+c{x}_2=qc\\ b{x}_2+d{x}_1=qd\end{array}\\ x_1=\frac{(d-b)c}{cd-ab}q,x_2=\frac{(c-a)d}{cd-ab}q\end{array}}$

Solución de la homogénea

Introduciendo el término armónico, Q₁sin(ωt+φ) y Q₂sin(ωt+φ) en cada una de las dos ecuaciones diferenciales homogéneas, tenemos

${\displaystyle \begin{array}{l}\{\begin{array}{l}-{\omega }^2{Q}_1+\frac{1}{L_1}\left(\frac{1}{C_1}+\frac{1}{C_3}\right)Q_1+\frac{1}{L_1{C}_3}{Q}_2=0\\ -{\omega }^2{Q}_2+\frac{1}{L_2}\left(\frac{1}{C_2}+\frac{1}{C_3}\right)Q_2+\frac{1}{L_2{C}_3}{Q}_1=0\end{array}\\ \{\begin{array}{l}-{\omega }^2{Q}_1+a{Q}_1+c{Q}_2=0\\ -{\omega }^2{Q}_2+b{Q}_2+d{Q}_1=0\end{array}\\ \left(\begin{array}{cc}a-{\omega }^2& c\\ d& b-{\omega }^2\end{array}\right)\left(\begin{array}{c}{Q}_1\\ Q_2\end{array}\right)=0\end{array}}$

El determinante de la matriz deberá ser cero

${\displaystyle \begin{array}{l}{\omega }^4-\left(a+b\right){\omega }^2+ab-cd=0\\ {\omega }_{\mathrm{1,2}}^2=\frac{a+b\pm \sqrt{{\left(a-b\right)}^2+4cd}}{2}\end{array}}$

Para cada una de las frecuencias ω₁ y ω₂ de los dos modos normales de vibración, los coeficientes Q₁ y Q₂ están relacionados, tomamos una de las dos ecuaciones, por ejemplo, la primera.

${\displaystyle \begin{array}{l}{r}_1=\frac{Q_2^{(1)}}{Q_1^{(1)}}=\frac{{\omega }_1^2-a}{c}\\ r_2=\frac{Q_2^{(2)}}{Q_1^{(2)}}=\frac{{\omega }_2^2-a}{c}\end{array}}$

Solución completa

La carga de cada uno de los dos condensadores q₁ y q₂ es la combinación lineal de los dos modos normales de vibración de frecuencias angulares ω₁ y ω₂

${\displaystyle \{\begin{array}{l}{q}_1=x_1+Q_1^{(1)}\sin ({\omega }_{1}t+{\phi }_1)+Q_1^{(2)}\sin ({\omega }_{2}t+{\phi }_2)\\ q_2=x_2+Q_2^{(1)}\sin ({\omega }_{1}t+{\phi }_1)+Q_2^{(2)}\sin ({\omega }_{2}t+{\phi }_2)=\\ r_1{Q}_1^{(1)}\sin ({\omega }_{1}t+{\phi }_1)+r_2{Q}_1^{(2)}\sin ({\omega }_{2}t+{\phi }_2)\\ q_3=q-q_1-q_2\end{array}}$

Las intensidades i son las derivadas de las cargas q respecto del tiempo t

${\displaystyle \{\begin{array}{l}{i}_1=Q_1^{(1)}{\omega }_1\cos ({\omega }_{1}t+{\phi }_1)+Q_1^{(2)}{\omega }_2\cos ({\omega }_{2}t+{\phi }_2)\\ i_2=r_1{Q}_1^{(1)}{\omega }_1\cos ({\omega }_{1}t+{\phi }_1)+r_2{Q}_1^{(2)}{\omega }_2\cos ({\omega }_{2}t+{\phi }_2)\\ i_3=i_2-i_1\end{array}}$

Hemos fijado unas condiciones iniciales sencillas, por ejemplo, el primer condensador de capacidad C₁ está cargado con carga q, el segundo, de capacidad C₂ está descargado, el tercero de capacidad C₃ está descargado. Las corrientes iniciales i₁=0 e i₂=0 y por tanto, i₃, son nulas

${\displaystyle t=\mathrm{0,}\{\begin{array}{l}{q}_1=q\\ q_2=0\\ q_3=0\end{array}\{\begin{array}{l}{i}_1=0\\ i_2=0\end{array}}$

Las condiciones iniciales determinan los dos coeficientes Q y las dos fases φ

${\displaystyle \begin{array}{l}\{\begin{array}{l}q=x_1+Q_1^{(1)}\sin {\phi }_1+Q_1^{(2)}\sin {\phi }_2\\ 0=x_2+r_1{Q}_1^{(1)}\sin {\phi }_1+r_2{Q}_1^{(2)}\sin {\phi }_2\end{array}\\ \{\begin{array}{l}0={\omega }_1{Q}_1^{(1)}\cos {\phi }_1+{\omega }_2{Q}_1^{(2)}\cos {\phi }_2\\ 0={\omega }_1{r}_1{Q}_1^{(1)}\cos {\phi }_1+{\omega }_2{r}_2{Q}_1^{(2)}\cos {\phi }_2\end{array}\end{array}}$

Las dos últimas ecuaciones implican que las fases φ₁=π/2 y φ₂=π/2

De las dos primeras ecuaciones, se obtiene

${\displaystyle \begin{array}{l}\{\begin{array}{l}q=x_1+Q_1^{(1)}+Q_1^{(2)}\\ 0=x_2+r_1{Q}_1^{(1)}+r_2{Q}_1^{(2)}\end{array}\\ Q_1^{(1)}=-\frac{r_2\left(q-x_1\right)+x_2}{r_1-r_2},Q_1^{(2)}=\frac{r_1\left(q-x_1\right)+x_2}{r_1-r_2}\end{array}}$

La carga q de cada condensador en función del tiempo t es

${\displaystyle \{\begin{array}{l}{q}_1=x_1-\frac{r_2\left(q-x_1\right)+x_2}{r_1-r_2}\sin \left({\omega }_{1}t+\frac{\pi }{2}\right)+\frac{r_1\left(q-x_1\right)+x_2}{r_1-r_2}\sin \left({\omega }_{2}t+\frac{\pi }{2}\right)=\\ x_1-\frac{r_2\left(q-x_1\right)+x_2}{r_1-r_2}\cos \left({\omega }_{1}t\right)+\frac{r_1\left(q-x_1\right)+x_2}{r_1-r_2}\cos \left({\omega }_{2}t\right)\\ q_2=x_2-r_1\frac{r_2\left(q-x_1\right)+x_2}{r_1-r_2}\cos \left({\omega }_{1}t\right)+r_2\frac{r_1\left(q-x_1\right)+x_2}{r_1-r_2}\cos \left({\omega }_{2}t\right)\\ q_3=q-q_1-q_2\end{array}}$

Caso particular

Cuando los osciladores son iguales, L₁=L₂=L, C₁=C₂=C se cumple que

${\displaystyle \begin{array}{l}a=b=\frac{1}{L}\left(\frac{1}{C}+\frac{1}{C_3}\right),c=d=\frac{1}{L{C}_3}\\ x_1=x_2=x_0=\frac{c}{c+a}q\end{array}}$

Las frecuencias de los modos normales de vibración son

${\displaystyle {\omega }_{\mathrm{1,2}}^2=a\pm c\{\begin{array}{l}{\omega }_1^2=\frac{1}{LC}\\ {\omega }_2^2=\frac{1}{L}\left(\frac{1}{C}+\frac{2}{C_3}\right)={\omega }_1^2+\frac{2}{L{C}_3}\end{array}}$

Los coeficientes r

${\displaystyle \begin{array}{l}{r}_1=\frac{Q_2^{(1)}}{Q_1^{(1)}}=-1\\ r_2=\frac{Q_2^{(2)}}{Q_1^{(2)}}=1\end{array}}$

La carga q de cada condensador en función del tiempo t es

${\displaystyle \{\begin{array}{l}{q}_1=x_0+\frac{q}{2}\cos \left({\omega }_{1}t\right)+\frac{q-2x_0}{2}\cos \left({\omega }_{2}t\right)\\ q_2=x_0-\frac{q}{2}\cos \left({\omega }_{1}t\right)+\frac{q-2x_0}{2}\cos \left({\omega }_{2}t\right)\\ q_3=q-q_1-q_2=2\left(q-2x_0\right)\cos \left(\frac{{\omega }_{2}t}{2}\right)\end{array}}$

Representamos q₁ y q₂ en función del tiempo t. Tomamos q=1, a=1.1, y c=0.1. Las frecuencias de los modos normales de vibración son próximas ω₁= 1 y ω₂= 1.0954 si el acoplamiento c es pequeño

a=1.1;
c=0.1;
%frecuencias de los modos normales de vibración
w1=sqrt(a-c);
w2=sqrt(a+c);
q=1; %carga inicial 
x0=c*q/(a+c);
q1=@(t) x0+q*cos(w1*t)/2+(q-2*x0)*cos(w2*t)/2;
q2=@(t) x0-q*cos(w1*t)/2+(q-2*x0)*cos(w2*t)/2;
hold on
fplot(q1,[0,70])
fplot(q2,[0,70])
hold off
grid on
xlabel('t')
ylabel('q')
title('Osciladores LC acoplados')

figure
q3=@(t) q-q1(t)-q2(t);
fplot(q3,[0,70])
grid on
xlabel('t')
ylabel('q_3')
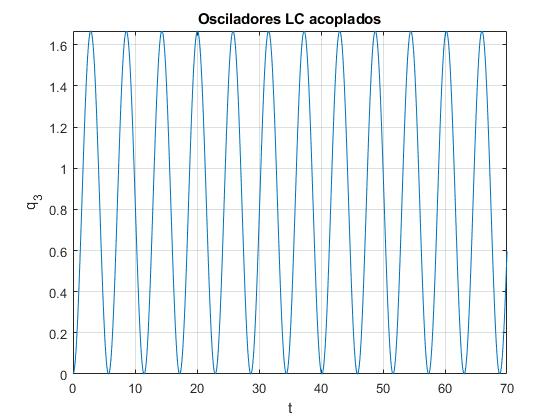
title('Osciladores LC acoplados')

Representamos q₃ en función del tiempo t

Referencias

Coupled Oscillations in RLC Circuits, Physics 231 Coupled Oscillations

Two Coupled LC Circuits. Richard Fitzpatrick, 2013-04-08