El movimiento de rotación de las espiras es producido por el movimiento de una turbina accionada por una corriente de agua en una central hidroeléctrica, o por un chorro de vapor en una central térmica. En el primer caso, una parte de la energía potencial agua embalsada se transforma en energía eléctrica; en el segundo caso, una parte de la energía química se transforma en energía eléctrica al quemar carbón u otro combustible fósil.

Cuando la espira gira, el flujo del campo magnético a través de la espira cambia con el tiempo. Se produce una fem. Los extremos de la espira se conectan a dos anillos que giran con la espira, tal como se ve en la figura. Las conexiones al circuito externo se hacen mediante escobillas estacionarias en contacto con los anillos.

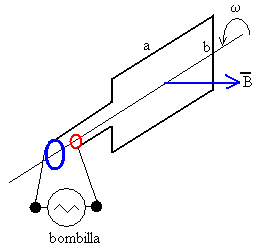
Si conectamos una bombilla al generador veremos que por el filamento de la bombilla circula una corriente que hace que se ponga incandescente, y emite tanta más luz cuanto mayor sea la velocidad con que gira la espira en el campo magnético.

Con este ejemplo, completamos las tres formas que hay de variar con el tiempo el flujo de un campo magnético a través de una espira,

${\displaystyle \Phi =\overrightarrow{B}·\overrightarrow{S}=BS\cos \theta }$

como producto escalar de dos vectores, el vector campo $\overrightarrow{B}$ y el vector superficie $\overrightarrow{S}$ .

• Cuando el campo cambia con el tiempo.
• Cuando el área de la espira cambia con el tiempo.
• Cuando el ángulo entre el vector campo $\overrightarrow{B}$ y el vector superficie $\overrightarrow{S}$ cambia con el tiempo. Situación que se discute en esta página.

Ley de Faraday

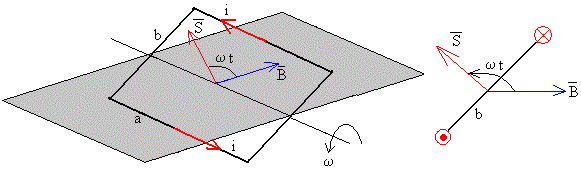
Supongamos que N espiras de área S giran con velocidad angular constante ω. Al cabo de un cierto tiempo t el ángulo que forma el campo magnético y la perpendicular al plano de la espira es ωt. El flujo del campo magnético B a través de una espira de área S es

${\displaystyle \Phi =\overrightarrow{B}·(N\overrightarrow{S})=BNS\cos \left(\omega t\right)}$

La fem en la espira es

${\displaystyle V_{\epsilon }=-\frac{d\Phi }{dt}=\omega BNS\sin (\omega t)}$

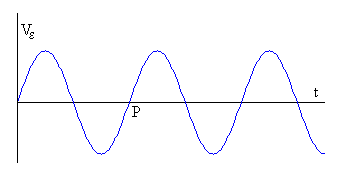
La fem V_ε varía sinusoidalmente con el tiempo, como se muestra en la figura. La fem alcanza su valor máximo en valor absoluto cuando ωt=π/2 ó 3π/2, cuando el flujo Φ es nulo (el campo magnético está en el plano de la espira), y es nula cuando ωt=0 ó π, cuando el flujo es máximo o mínimo (el campo magnético es perpendicular al plano de la espira).

Ecuación del circuito

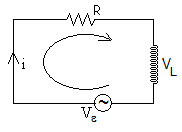
Consideremos un circuito formado por la fem alterna V_ε, la resistencia R y l autoinduccción L de las N espiras. La ecuación del circuito es

${\displaystyle \begin{array}{l}iR=V_{\epsilon }-L\frac{di}{dt}\\ L\frac{di}{dt}+iR=BNS\omega \sin \left(\omega t\right)\end{array}}$

La solución de la ecuación diferencial homogénea es

${\displaystyle i_h=F\exp \left(-\frac{R}{L}t\right)}$

La solución particular

${\displaystyle i_p=C\sin \left(\omega t\right)+D\cos \left(\omega t\right)}$

Introduciendo la solución particular en la ecuaciín diferencial, obtenemos los coeficientes C y D

${\displaystyle \begin{array}{l}L\omega \left(C\cos \left(\omega t\right)-D\sin \left(\omega t\right)\right)+R\left(C\sin \left(\omega t\right)+D\cos \left(\omega t\right)\right)=BNS\omega \sin \left(\omega t\right)\\ D=-\frac{L{\omega }^2}{L^2{\omega }^2+R^2}BNS,C=\frac{R\omega }{L^2{\omega }^2+R^2}BNS\\ i_p=\frac{\omega }{L^2{\omega }^2+R^2}BNS\left(R\sin \left(\omega t\right)-L\omega \cos \left(\omega t\right)\right)\end{array}}$

La solución completa es la suma de i_p e i_h

${\displaystyle i=F\exp \left(-\frac{R}{L}t\right)+\frac{\omega }{L^2{\omega }^2+R^2}BNS\left(R\sin \left(\omega t\right)-L\omega \cos \left(\omega t\right)\right)}$

El coeficiente F se determina a partir de las condiciones iniciales, en el instante t=0, i=0

${\displaystyle \begin{array}{l}0=F-\frac{L{\omega }^2}{L^2{\omega }^2+R^2}BNS\\ i=\frac{\omega }{L^2{\omega }^2+R^2}BNS\left(L\omega \exp \left(-\frac{R}{L}t\right)+R\sin \left(\omega t\right)-L\omega \cos \left(\omega t\right)\right)\end{array}}$

El término transitorio, exp(-Rt/L) tiende a cero a medida que pasa el tiempo. Después de un tiempo relativamente corto, ya que la resistencia R suele ser mucho mayor que la autoinducción L, podemos prescindir de este término

${\displaystyle \begin{array}{l}{i}_{\infty }=\frac{\omega }{L^2{\omega }^2+R^2}BNS\left(R\sin \left(\omega t\right)-L\omega \cos \left(\omega t\right)\right)\\ i_{\infty }=\frac{\omega }{\sqrt{L^2{\omega }^2+R^2}}BNS·\sin \left(\omega t-\phi \right),\tan \phi =\frac{L\omega }{R}\end{array}}$

La corriente va retrasada respecto de la fem V_ε un ángulo φ.

Momento que ejerce el campo magnético sobre la corriente inducida en las espiras

En la página titulada, Fuerza y momento sobre una espira, hemos calculado el momento que ejerce el campo magnético sobre la corriente de intensidad i que circula por una espira

${\displaystyle \begin{array}{l}\overrightarrow{M}=\overrightarrow{\mu }\times \overrightarrow{B}\\ \overrightarrow{M}=\left(i_{\infty }NS\widehat{n}\right)\times \overrightarrow{B}\\ M=i_{\infty }NSB\sin \left(\omega t\right)\\ M=\frac{\omega }{L^2{\omega }^2+R^2}{B}^2{N}^2{S}^2\left(R{\sin }^2\left(\omega t\right)-L\omega \sin \left(\omega t\right)\cos \left(\omega t\right)\right)\end{array}}$

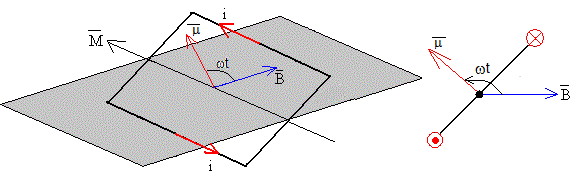
El momento $\overrightarrow{M}$, tiene la dirección del eje de rotación de la espira y sentido contrario a la velocidad angular de rotación

Valor medio

Se define el valor medio

${\displaystyle <f(t)>=\frac{1}{P}{\displaystyle \underset{0}{\overset{P}{\int }}f(t)·dt}}$

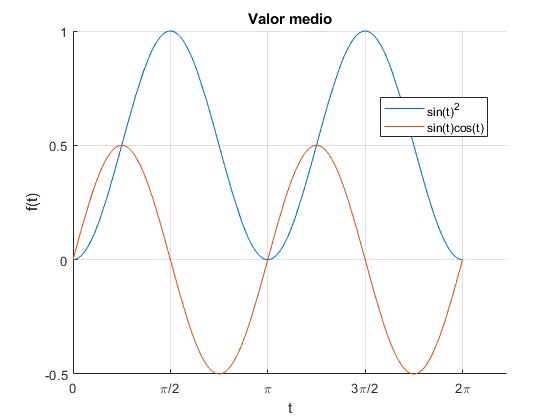
Calculamos el valor medio de de <sin²(ωt)> y <sin(ωt)·cos(ωt)>

Como vemos en la figura, sin²(t) es una función periódica de periodo π. Del mismo periodo es sin(t)·cos(t)

hold on
fplot(@(t) sin(t).^2, [0,2*pi])
fplot(@(t) sin(t).*cos(t), [0,2*pi])
hold off
grid on
set(gca,'XTick',0:pi/2:2*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
legend('sin(t)^2','sin(t)cos(t)','Location','best')
xlabel('t')
ylabel('f(t)')
title('Valor medio')

>> syms t;
>> int(sin(t)^2,t,0,pi)/pi
ans =1/2
>> int(sin(t)*cos(t),t,0,pi)/pi
ans =0

El resultado es, <sin²(ωt)>=1/2 y <sin(ωt)·cos(ωt)>=0

El valor medio del momento es

${\displaystyle \begin{array}{l}<M>=\frac{\omega }{L^2{\omega }^2+R^2}{B}^2{N}^2{S}^2\left(R<{\sin }^2\left(\omega t\right)>-L\omega <\sin \left(\omega t\right)\cos \left(\omega t\right)>\right)\\ <M>=\frac{1}{2}\frac{R\omega }{L^2{\omega }^2+R^2}{B}^2{N}^2{S}^2\end{array}}$

Referencias

Fotografía tomada en la VIII Edición del Concurso Ciencia en Acción Zaragoza (2007): Albert Agraz Sánchez, Santiago Clúa. Detector de movimiento por inducción magnética. Universitat de Lleida.

J. Pierrus. Solved Problems in Classical Electromagnetism. Analytical and numerical solutions with comments. Oxford University Press (2018). Question 5.7, pp. 257-259