Ley de Ohm

Por una porción de conductor de longitud l, sección de radio a, por el que circula una corriente de intensidad i, la ley de Ohm se escribe

${\displaystyle V\text{'}-V=iR,R=\frac{1}{\sigma }\frac{l}{\pi a^2}}$

V'-V es la diferencia de potencial entre dos puntos de la superficie del conductor separados l

La resistencia es directamente proporcional a la longitud l de la porción de conductor e inversamente proporcional al área (πa²) de su sección. La constante de proporcionalidad se denomina resistividad 1/σ y a a la inversa, σ conductividad del material. Por ejemplo, para el cobre la resistividad es 0.0175·10^-6 Ω·m

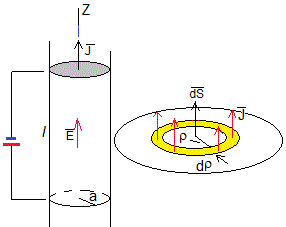
Cuando la intensidad i no está uniformente distribuida en la sección del conductor, la ley de Ohm se expresa en términos del vector densidad de corriente $\overrightarrow{J}$, cuyo módulo es el cociente entre la intensidad I y el área de la sección (πa²), para una corriente uniformente distribuida en la sección del conductor

${\displaystyle \begin{array}{l}{E}_{z}l=I\frac{1}{\sigma }\frac{l}{\pi a^2}\\ E_z=\frac{1}{\sigma }{J}_z\\ \overrightarrow{J}=\sigma \overrightarrow{E}\end{array}}$

Para una corriente que no está uniformente distribuida en su sección, la intensidad es

${\displaystyle I={\displaystyle \int \overrightarrow{J}·\overrightarrow{dS}}={\displaystyle \underset{0}{\overset{a}{\int }}{J}_z(\rho )\left(2\pi \rho ·d\rho \right)}}$

Cuando circula una corriente alterna, I(t)=I₀exp(iωt), de frecuencia angular ω, la impedancia Z del conductor es

${\displaystyle Z=Z_R+Z_L=R-\text{i}\omega L}$

Siendo L el coeficiente de autoinducción de la porción l del conductor

Ley de Ampère

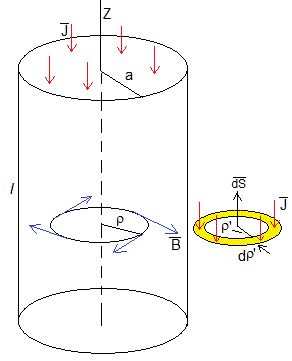
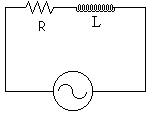
La ley de Ampère-Maxwell es

${\displaystyle {\displaystyle \oint \overrightarrow{B}·\overrightarrow{dl}=}{\mu }_{0}i+{\epsilon }_0{\mu }_0\frac{d}{dt}{\displaystyle \oint \overrightarrow{E}·\overrightarrow{dl}}}$

Despreciamos el segundo término, las denominadas corrientes de desplazamiento. El campo magnético en el interior del conductor es

${\displaystyle \begin{array}{l}{\displaystyle \oint \overrightarrow{B}·\overrightarrow{dl}=}{\mu }_o{\displaystyle \int \overrightarrow{J}·\overrightarrow{dS}}\\ B_{\phi }·2\pi \rho =-{\mu }_o{\displaystyle \underset{0}{\overset{\rho }{\int }}{J}_z\left(2\pi \rho \text{'}\right)d\rho \text{'}}\\ B_{\phi }=-{\mu }_o\frac{1}{\rho }{\displaystyle \underset{0}{\overset{\rho }{\int }}{J}_z\rho \text{'}d\rho \text{'}}\end{array}}$

El campo magnético B_φ es tangente a la circunferencia de radio ρ y en el sentido indicado en la figura, de acuerdo con la regla de la mano derecha

Ley de Faraday

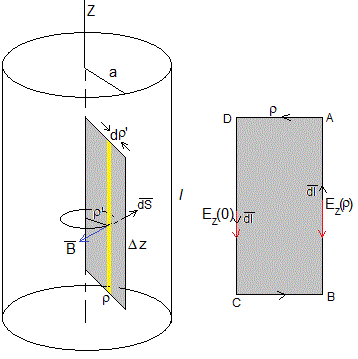
Como la intesidad de la corriente es variable con el tiempo (de frecuencia ω), el campo magnético B_φ es variable con el tiempo, el flujo a través de la superficie ABCD es variable con el tiempo. Aplicamos la ley de Faraday para calcular el campo eléctrico en el conductor.

${\displaystyle {\displaystyle \oint \overrightarrow{E}·\overrightarrow{dl}=}-\frac{d}{dt}{\displaystyle \int \overrightarrow{B}·\overrightarrow{dS}}}$

El flujo del campo magnético B_φ a través del área del rectángulo de lados ρ y Δz, es

${\displaystyle \begin{array}{l}{\displaystyle \int \overrightarrow{B}·\overrightarrow{dS}}=-{\displaystyle \underset{0}{\overset{\rho }{\int }}{B}_{\phi }}(\Delta z·d\rho \text{'})=\\ -\Delta z·{\displaystyle \underset{0}{\overset{\rho }{\int }}{B}_{\phi }·}d\rho \text{'}\end{array}}$

La circulación del campo eléctrico a lo largo del camino ABCD es

${\displaystyle \begin{array}{l}{\displaystyle \oint \overrightarrow{E}·\overrightarrow{dl}={\displaystyle \underset{A}{\overset{B}{\int }}\overrightarrow{E}·\overrightarrow{dl}+}}{\displaystyle \underset{B}{\overset{C}{\int }}\overrightarrow{E}·\overrightarrow{dl}+}{\displaystyle \underset{C}{\overset{D}{\int }}\overrightarrow{E}·\overrightarrow{dl}+{\displaystyle \underset{D}{\overset{A}{\int }}\overrightarrow{E}·\overrightarrow{dl}}=}\\ -E_z(\rho )·\Delta z+0+E_z(0)·\Delta z+0=-\left(E_z(\rho )-E_z(0)\right)\Delta z\end{array}}$

El resultado de la aplicación de la ley de Faraday, es

${\displaystyle E_z(\rho )-E_z(0)=-\frac{d}{dt}{\displaystyle \underset{0}{\overset{\rho }{\int }}{B}_{\phi }·}d\rho \text{'}}$

Aplicamos la ley de Ohm, relacionando el campo eléctrico y la densidad de corriente, $\overrightarrow{J}=\sigma \overrightarrow{E}$

${\displaystyle \begin{array}{l}{J}_z(\rho ,t)-J_z(\mathrm{0,}t)=-\sigma \frac{d}{dt}{\displaystyle \underset{0}{\overset{\rho }{\int }}{B}_{\phi }·}d\rho \text{'}\\ J_z(\rho ,t)-J_z(\mathrm{0,}t)={\mu }_o\sigma \frac{d}{dt}\left({\displaystyle \underset{0}{\overset{\rho }{\int }}\left(\frac{1}{\rho \text{'}}{\displaystyle \underset{0}{\overset{\rho \text{'}}{\int }}{J}_z(\rho \text{'}\text{'},t)·\rho \text{'}\text{'}d\rho \text{'}\text{'}}\right)}d\rho \text{'}\right)\end{array}}$

Por el conductor circula una corriente alterna de frecuencia angular ω

${\displaystyle J_z(\rho ,t)=J_z(\rho )·\exp \left(-\text{i}\omega t\right)}$

La ecuación se simplifica, al separarse las variables t y ρ

${\displaystyle \begin{array}{l}{J}_z(\rho )e^{-\text{i}\omega t}-J_z(0)e^{-\text{i}\omega t}=-\text{i}\omega {\mu }_o\sigma \left\{{\displaystyle \underset{0}{\overset{\rho }{\int }}\left(\frac{1}{\rho \text{'}}{\displaystyle \underset{0}{\overset{\rho \text{'}}{\int }}{J}_z(\rho \text{'}\text{'})\rho \text{'}\text{'}d\rho \text{'}\text{'}}\right)d\rho \text{'}}\right\}{e}^{-\text{i}\omega t}\\ J_z(\rho )=J_z(0)-\text{i}\omega {\mu }_o\sigma {\displaystyle \underset{0}{\overset{\rho }{\int }}\left(\frac{1}{\rho \text{'}}{\displaystyle \underset{0}{\overset{\rho \text{'}}{\int }}{J}_z(\rho \text{'}\text{'})\rho \text{'}\text{'}d\rho \text{'}\text{'}}\right)d\rho \text{'}}\end{array}}$

Se define espesor pelicular, el parámetro δ, llegando a la ecuación

${\displaystyle \begin{array}{l}\delta =\sqrt{\frac{2}{\omega {\mu }_0\sigma }}\\ J_z(\rho )=J_z(0)-\frac{2\text{i}}{{\delta }^2}{\displaystyle \underset{0}{\overset{\rho }{\int }}\left(\frac{1}{\rho \text{'}}{\displaystyle \underset{0}{\overset{\rho \text{'}}{\int }}{J}_z(\rho \text{'}\text{'})\rho \text{'}\text{'}d\rho \text{'}\text{'}}\right)d\rho \text{'}}\end{array}}$

Método de las aproximaciones sucesivas

Para obtener la solución J_z(ρ) de esta ecuación, utilizamos el método de las aproxiamciones sucesivas

• Primera aproximación: dado J_z(ρ)=J₀, que es constante, obtenemos J₁(ρ)

${\displaystyle \begin{array}{l}{J}_1(\rho )=J_0-\frac{2\text{i}}{{\delta }^2}{\displaystyle \underset{0}{\overset{\rho }{\int }}\left(\frac{1}{\rho \text{'}}{\displaystyle \underset{0}{\overset{\rho \text{'}}{\int }}{J}_0\rho \text{'}\text{'}d\rho \text{'}\text{'}}\right)d\rho \text{'}}\\ J_1(\rho )=J_0-\frac{2\text{i}}{{\delta }^2}{J}_0{\displaystyle \underset{0}{\overset{\rho }{\int }}\left(\frac{1}{\rho \text{'}}\frac{\rho {\text{'}}^2}{2}\right)d\rho \text{'}}\\ J_1(\rho )=J_0-\frac{2\text{i}}{{\delta }^2}\frac{J_0}{2}{\displaystyle \underset{0}{\overset{\rho }{\int }}\rho \text{'}d\rho \text{'}}\\ J_1(\rho )=J_0\left(1-2\text{i}\frac{1}{2·2}{\left(\frac{\rho }{\delta }\right)}^2\right)\end{array}}$

• Segunda aproximación, dado J₁(ρ), obtenemos J₂(ρ)

${\displaystyle \begin{array}{l}{J}_2(\rho )=J_0-\frac{2\text{i}}{{\delta }^2}{\displaystyle \underset{0}{\overset{\rho }{\int }}\left(\frac{1}{\rho \text{'}}{\displaystyle \underset{0}{\overset{\rho \text{'}}{\int }}{J}_1\rho \text{'}\text{'}d\rho \text{'}\text{'}}\right)d\rho \text{'}}\\ J_2(\rho )=J_0-\frac{2\text{i}}{{\delta }^2}{J}_0{\displaystyle \underset{0}{\overset{\rho }{\int }}\left(\frac{1}{\rho \text{'}}\left\{\frac{\rho {\text{'}}^2}{2}-2\text{i}\frac{1}{2·2}\frac{1}{4}\frac{\rho {\text{'}}^4}{{\delta }^2}\right\}\right)d\rho \text{'}}\\ J_2(\rho )=J_0-\frac{2\text{i}}{{\delta }^2}{J}_0\left(\frac{{\rho }^2}{2·2}-2\text{i}\frac{1}{2·2}\frac{1}{4·4}\frac{{\rho }^4}{{\delta }^2}\right)\\ J_2(\rho )=J_0\left(1-2\text{i}\frac{1}{2·2}{\left(\frac{\rho }{\delta }\right)}^2+{\left(2\text{i}\right)}^2\frac{1}{2·2}\frac{1}{4·4}{\left(\frac{\rho }{\delta }\right)}^4\right)\end{array}}$

• Tercera aproximación, dado J₂(ρ), obtenemos J₃(ρ)

${\displaystyle \begin{array}{l}{J}_3(\rho )=J_0-\frac{2\text{i}}{{\delta }^2}{\displaystyle \underset{0}{\overset{\rho }{\int }}\left(\frac{1}{\rho \text{'}}{\displaystyle \underset{0}{\overset{\rho \text{'}}{\int }}{J}_2\rho \text{'}\text{'}d\rho \text{'}\text{'}}\right)d\rho \text{'}}\\ J_3(\rho )=J_0-\frac{2\text{i}}{{\delta }^2}{J}_0{\displaystyle \underset{0}{\overset{\rho }{\int }}\left(\frac{1}{\rho \text{'}}\left\{\frac{\rho {\text{'}}^2}{2}-2\text{i}\frac{1}{2·2}\frac{1}{4}\frac{\rho {\text{'}}^4}{{\delta }^2}+{\left(2\text{i}\right)}^2\frac{1}{2·2}\frac{1}{4·4}\frac{1}{6}\frac{\rho {\text{'}}^6}{{\delta }^4}\right\}\right)d\rho \text{'}}\\ J_3(\rho )=J_0-\frac{2\text{i}}{{\delta }^2}{J}_0\left(\frac{{\rho }^2}{2·2}-2\text{i}\frac{1}{2·2}\frac{1}{4·4}\frac{{\rho }^4}{{\delta }^2}+{\left(2\text{i}\right)}^2\frac{1}{2·2}\frac{1}{4·4}\frac{1}{6·6}\frac{{\rho }^6}{{\delta }^4}\right)\\ J_3(\rho )=J_0\left(1-2\text{i}\frac{1}{2·2}{\left(\frac{\rho }{\delta }\right)}^2+{\left(2\text{i}\right)}^2\frac{1}{2·2}\frac{1}{4·4}{\left(\frac{\rho }{\delta }\right)}^4-{\left(2\text{i}\right)}^3\frac{1}{2·2}\frac{1}{4·4}\frac{1}{6·6}{\left(\frac{\rho }{\delta }\right)}^6\right)\end{array}}$

• Aproximación, n

${\displaystyle J_n(\rho )=J_0\left(1+{\displaystyle \sum _{k=1}^n\frac{{\left(-2\text{i}\right)}^k}{{\left(2·4·6·\mathrm{...}·2k\right)}^2}{\left(\frac{\rho }{\delta }\right)}^{2k}}\right)=J_0\left({\displaystyle \sum _{k=0}^n{\left(\frac{-\text{i}}{2}\right)}^k\frac{1}{{\left(k!\right)}^2}{\left(\frac{\rho }{\delta }\right)}^{2k}}\right)}$

La solución buscada J_z(ρ) es la serie

${\displaystyle J_z(\rho )=J_z(0)\left({\displaystyle \sum _{k=0}^{\infty }{\left(\frac{-\text{i}}{2}\right)}^k\frac{1}{{\left(k!\right)}^2}{\left(\frac{\rho }{\delta }\right)}^{2k}}\right)}$

En el artículo citado en las referencias, se demuestra que la serie es convergente y que J_z(ρ) es la solución de la ecuación

${\displaystyle J_z(\rho )=J_z(0)-\frac{2\text{i}}{{\delta }^2}{\displaystyle \underset{0}{\overset{\rho }{\int }}\left(\frac{1}{\rho \text{'}}{\displaystyle \underset{0}{\overset{\rho \text{'}}{\int }}{J}_z(\rho \text{'}\text{'})\rho \text{'}\text{'}d\rho \text{'}\text{'}}\right)d\rho \text{'}}}$

Densidad de corriente

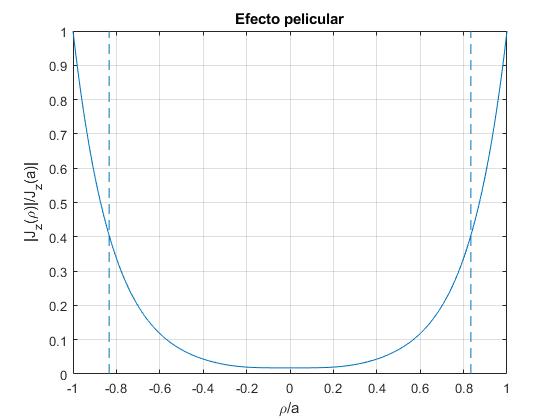
Representamos el valor absoluto del cociente |J_z(ρ)|/|J_z(a)|, para a/δ=6. Las líneas verticales distan δ de la superficie del conductor. La corriente circula por una porción de la sección del conductor, la mayor parte, por el anillo de radio interior a-δ y radio exterior, a, y muy poca por el eje del conductor

function skin_3
    a=1;
    r=6;
    delta=a/r;
    den=abs(serie(a));
    x=linspace(0,a,100);
    y=abs(serie(x))/den;
    plot([fliplr(-x) x], [fliplr(y) y]);
    line([-a+delta,-a+delta],[0,1],'lineStyle','--')
    line([a-delta,a-delta],[0,1],'lineStyle','--')
    xlabel('\rho/a')
    ylabel('|J_z(\rho)|/J_z(a)|')
    grid on
    title('Efecto pelicular')
    
    function res=serie(x)   
        res=0;
        for k=0:50
            res=res+(-1i/2)^k*((x/delta).^k/factorial(k)).^2;
        end
    end
end

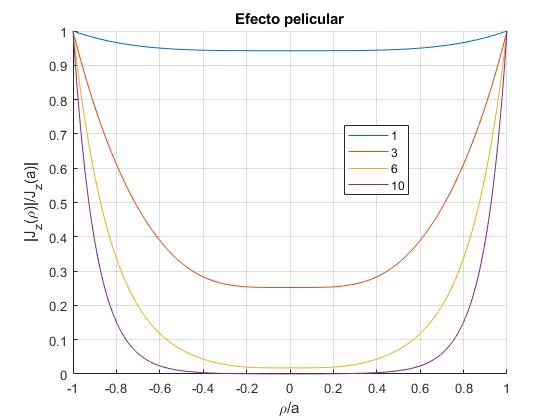
Representamos el valor absoluto del cociente |J_z(ρ)|/|J_z(a)|, para varios valores de a/δ=1, 3, 6, 10.

function skin
    a=1;
    hold on
    for r=[1,3,6,10]
         delta=a/r;
         den=abs(serie(a));
         x=linspace(0,a,100);
         y=abs(serie(x))/den;
        plot([fliplr(-x) x], [fliplr(y) y], 'displayName',num2str(r));
    end
    
    hold off
    xlabel('\rho/a')
    ylabel('|J_z(\rho)|/J_z(a)|')
    legend('-DynamicLegend','location','best')
    grid on
    title('Efecto pelicular')
    
    function res=serie(x)   
        res=0;
        for k=0:200
            res=res+(-1i/2)^k*((x/delta).^k/factorial(k)).^2;
        end
    end
end

Sea un conductor de cobre de radio 0.5 mm. La resistividad del cobre es 0.0175·10^-6 Ω·m. Para el cociente a/δ=3, calculamos la frecuencia f de la corriente alterna

${\displaystyle \begin{array}{l}\delta =\sqrt{\frac{2}{\omega {\mu }_0\sigma }}\\ \delta =\frac{0.5·{10}^{-3}}{3}=\sqrt{\frac{2·0.0175·{10}^{-6}}{2\pi f·4\pi ·{10}^{-7}}}\end{array}}$

El resultado es f=1.596·10⁵ Hz=159.6 kHz. Del mismo modo,

• Para a/δ=1, f=17.73 kHz
• Para a/δ=6, f=638.3 kHz
• Para a/δ=10, f=1.773 MHz

Impedancia

La impedancia por unidad de longitud es

${\displaystyle Z=\frac{1}{\Delta z}\frac{V_{\rho =a}}{I}=\frac{E_z(a)}{{\displaystyle \underset{0}{\overset{a}{\int }}{J}_z(\rho )\left(2\pi \rho ·d\rho \right)}}=\frac{J_z(a)}{2\pi \sigma {\displaystyle \underset{0}{\overset{a}{\int }}{J}_z(\rho )·\rho ·d\rho }}}$

Resolvemos la integral del denominador

${\displaystyle \begin{array}{l}{J}_z(0)\left({\displaystyle \sum _{k=0}^{\infty }{\left(\frac{-\text{i}}{2}\right)}^k\frac{1}{{\left(k!\right)}^2}\frac{1}{{\delta }^{2k}}{\displaystyle \underset{0}{\overset{a}{\int }}{\rho }^{2k+1}d\rho }}\right)=J_z(0)\left({\displaystyle \sum _{k=0}^{\infty }{\left(\frac{-\text{i}}{2}\right)}^k\frac{1}{{\left(k!\right)}^2}\frac{1}{{\delta }^{2k}}{\displaystyle \underset{0}{\overset{a}{\int }}{\rho }^{2k+1}d\rho }}\right)=\\ J_z(0)\left({\displaystyle \sum _{k=0}^{\infty }{\left(\frac{-\text{i}}{2}\right)}^k\frac{1}{{\left(k!\right)}^2}\frac{a^{2k+2}}{{\delta }^{2k}}\frac{1}{2k+2}}\right)=\frac{a^2}{2}{J}_z(0){\displaystyle \sum _{k=0}^{\infty }{\left(\frac{-\text{i}}{2}\right)}^k\frac{1}{{\left(k!\right)}^2}\frac{1}{k+1}{\left(\frac{a}{\delta }\right)}^{2k}}\end{array}}$

La impedancia Z por unidad de longitud, es el cociente entre dos series

${\displaystyle Z=\frac{1}{\pi \sigma a^2}\frac{{\displaystyle \sum _{k=0}^{\infty }{\left(\frac{-\text{i}}{2}\right)}^k\frac{1}{{\left(k!\right)}^2}{\left(\frac{a}{\delta }\right)}^{2k}}}{{\displaystyle \sum _{k=0}^{\infty }{\left(\frac{-\text{i}}{2}\right)}^k\frac{1}{{\left(k!\right)}^2}\frac{1}{k+1}{\left(\frac{a}{\delta }\right)}^{2k}}}}$

El factor que multiplica es la resistencia por unidad de longitud, R₀=1/(πσa²) cuando circula corriente continua por el conductor, ω=0

Parte real

La impedancia Z es un número complejo, la parte real Re, es la resistencia R por unidad de longitud

${\displaystyle R=R_0·\mathrm{Re}\left(\frac{{\displaystyle \sum _{k=0}^{\infty }{\left(\frac{-\text{i}}{2}\right)}^k\frac{1}{{\left(k!\right)}^2}{\left(\frac{a}{\delta }\right)}^{2k}}}{{\displaystyle \sum _{k=0}^{\infty }{\left(\frac{-\text{i}}{2}\right)}^k\frac{1}{{\left(k!\right)}^2}\frac{1}{k+1}{\left(\frac{a}{\delta }\right)}^{2k}}}\right)}$

Representamos la resistencia R por unidad de longitud, la parte real de Z/R₀ en función de a/δ

function skin_1
    x=linspace(0,5,100); %a/delta
    Z=serie_num(x)./serie_den(x);
    plot(x,real(Z))
    xlabel('a/\delta')
    ylabel('Re(Z)/r_0')
    grid on
    title('Parte real')
    
    function res=serie_num(x)   
        res=0;
        for k=0:100
            res=res+(-1i/2)^k*(x.^k/factorial(k)).^2;
        end
    end
    function res=serie_den(x)   
        res=0;
        for k=0:100
            res=res+(-1i/2)^k*(x.^k/factorial(k)).^2/(k+1);
        end
    end
end

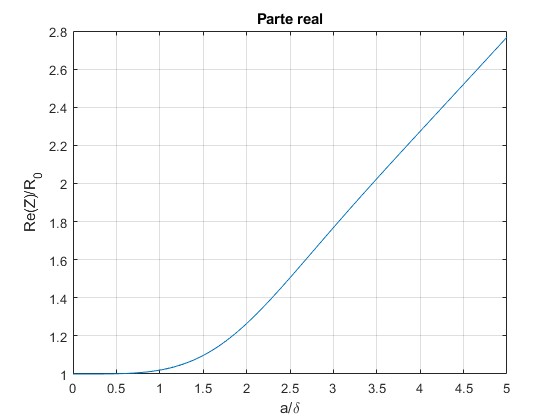
La respresentación gráfica nos sugiere que habrá dos posibles expresiones asintóticas para la resistencia, cuando la frecuencia es pequeña, ω→0 y cuando es grande, ω→∞

• Para un conductor de cobre (resistividad, 0.0175·10^-6 Ωm) de radio a=0.5 mm, la resistencia por unidad de longitud cuando conduce corriente continua es,

${\displaystyle R_0=\frac{0.0175·{10}^{-6}}{\pi {\left(0.5·{10}^{-3}\right)}^2}=\text{0}\text{.0223}{\text{Ωm}}^{-1}}$

• Cuando conduce una corriente alterna de frecuencia f=159.6 kHz, lo que corresponde al cociente a/δ=3, obtenemos

...
    x=3; %a/delta
    disp(real(serie_num(x)/serie_den(x)))

    1.7681

La resistencia por unidad de longitud es 1.7681·R₀ más grande

• Para la frecuencia f=638.3 kHz, lo que corresponde al cociente a/δ=6, obtenemos 3.2652·R₀

Parte imaginaria

Representamos la parte imaginaria de Z/R₀ en función de a/δ

function skin_3
    x=linspace(0,5,100); %a/delta
    Z=serie_num(x)./serie_den(x);
    plot(x,imag(Z))
    xlabel('a/\delta')
    ylabel('Imag(Z)/R_0')
    grid on
    title('Parte imaginaria')
     
    function res=serie_num(x)   
        res=0;
        for k=0:100
            res=res+(-1i/2)^k*(x.^k/factorial(k)).^2;
        end
    end
    function res=serie_den(x)   
        res=0;
        for k=0:100
            res=res+(-1i/2)^k*(x.^k/factorial(k)).^2/(k+1);
        end
    end
end

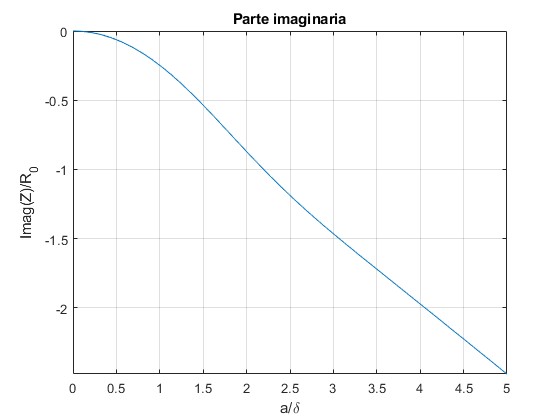
La parte imaginaria, Imag,es la impedancia inductiva -iωL por unidad de longitud del conductor. Teniendo en cuenta la definición del espesor δ

${\displaystyle \begin{array}{l}-\omega L=\frac{1}{\pi \sigma a^2}\text{Imag}\left(\frac{{\displaystyle \sum _{k=0}^{\infty }{\left(\frac{-\text{i}}{2}\right)}^k\frac{1}{{\left(k!\right)}^2}{\left(\frac{a}{\delta }\right)}^{2k}}}{{\displaystyle \sum _{k=0}^{\infty }{\left(\frac{-\text{i}}{2}\right)}^k\frac{1}{{\left(k!\right)}^2}\frac{1}{k+1}{\left(\frac{a}{\delta }\right)}^{2k}}}\right)\\ -\frac{2}{{\delta }^2{\mu }_0\sigma }L=\frac{1}{\pi \sigma a^2}\text{Imag}\left(\frac{{\displaystyle \sum _{k=0}^{\infty }{\left(\frac{-\text{i}}{2}\right)}^k\frac{1}{{\left(k!\right)}^2}{\left(\frac{a}{\delta }\right)}^{2k}}}{{\displaystyle \sum _{k=0}^{\infty }{\left(\frac{-\text{i}}{2}\right)}^k\frac{1}{{\left(k!\right)}^2}\frac{1}{k+1}{\left(\frac{a}{\delta }\right)}^{2k}}}\right)\\ L=-{\left(\frac{\delta }{a}\right)}^2\frac{{\mu }_0}{2\pi }\text{Imag}\left(\frac{{\displaystyle \sum _{k=0}^{\infty }{\left(\frac{-\text{i}}{2}\right)}^k\frac{1}{{\left(k!\right)}^2}{\left(\frac{a}{\delta }\right)}^{2k}}}{{\displaystyle \sum _{k=0}^{\infty }{\left(\frac{-\text{i}}{2}\right)}^k\frac{1}{{\left(k!\right)}^2}\frac{1}{k+1}{\left(\frac{a}{\delta }\right)}^{2k}}}\right)\end{array}}$

Representamos el coeficiente de autoinducción L/(μ₀/4π)=L·10⁷ por unidad de longitud, la parte imaginaria de Z multiplicada por el factor (δ/a)² en función de δ/a

function skin_2
    xx=linspace(0,1.6,100);  %delta/a
    r=-2*serie_num(1./xx).*(xx.^2)./serie_den(1./xx);
    plot(xx,imag(r))
    xlabel('\delta/a')
    ylabel('L/(\mu_0/4\pi)')
    grid on
    title('Efecto pelicular')    
    
    function res=serie_num(x)   
        res=0;
        for k=0:130
            res=res+(-1i/2)^k*(x.^k/factorial(k)).^2;
        end
    end
    function res=serie_den(x)   
        res=0;
        for k=0:130
            res=res+(-1i/2)^k*(x.^k/factorial(k)).^2/(k+1);
        end
    end
end

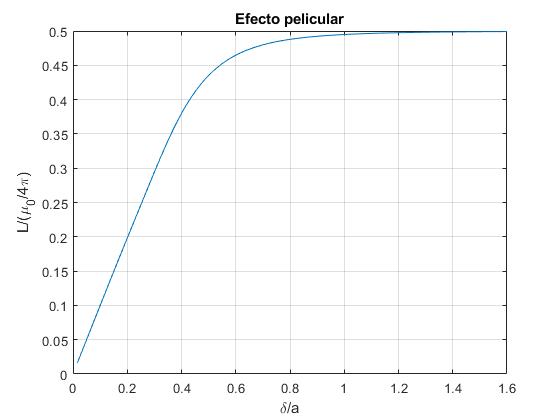
La respresentación gráfica nos sugiere que habrá dos posibles expresiones asintóticas para el coeficiente de autoinducción, cuando la frecuencia es pequeña, ω→0 y cuando es grande, ω→∞

Efecto pelicular. Caso general

En la página titulada Propagación de ondas electromagnéticas. Ecuaciones de Fresnel. en el apartado 'Ecuaciones de Maxwell' llegamos a la siguiente expresión para el campo eléctrico

${\displaystyle {\nabla }^2\overrightarrow{E}-\epsilon \mu \frac{{\partial }^2\overrightarrow{E}}{\partial t^2}=\frac{1}{\epsilon }\overrightarrow{\nabla }{\rho }_f+\mu \frac{\partial \overrightarrow{J_f}}{\partial t}}$

La ley de Ohm

${\displaystyle \overrightarrow{J_f}=\sigma \overrightarrow{E}}$

En las regiones en las que se anulan ρ_f, no hay densidad de carga libre, se obtiene la ecuación de ondas homogénea

${\displaystyle {\nabla }^2\overrightarrow{E}=\epsilon \mu \frac{{\partial }^2\overrightarrow{E}}{\partial t^2}+\mu \sigma \frac{\partial \overrightarrow{E}}{\partial t}}$

El primer término del segundo miembro, relacionado con la corriente de desplamiento, se despreció en la primera parte de esta página

Consideremos un cable en forma de un largo cilindro de radio a hecho de un material de conductividad σ, permitividad eléctrica ε y permitividad magnética μ, que transporta una corriente alterna

${\displaystyle I=I_0\exp \left(-i\omega t\right)}$

de amplitud I₀ y frecuencia angular ω.

Elegimos un sistema de coordenadas cilíndricas, el eje Z coincide con el eje del cable. El vector densidad de corriente J_z apunta a lo largo del eje Z. Por simetría, solamente dependerá de la distancia radial ρ, E_z=σ·J_z. Las componentes E_ρ=0 y E_φ=0 serán nulas

${\displaystyle \overrightarrow{E}=\frac{J_z\left(\rho \right)}{\sigma }\exp \left(-i\omega t\right)\widehat{k}}$

Expresamos la ecuación diferencial del campo eléctrico en coordenadas cilíndricas

${\displaystyle \begin{array}{l}\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial \overrightarrow{E}}{\partial \rho }\right)=\epsilon \mu \frac{{\partial }^2\overrightarrow{E}}{\partial t^2}+\mu \sigma \frac{\partial \overrightarrow{E}}{\partial t}\\ \frac{1}{\rho }\frac{d}{d\rho }\left(\rho \frac{d{J}_z}{d\rho }\right)\frac{1}{\sigma }=-\epsilon \mu \frac{{\omega }^2}{\sigma }{J}_z-i\omega \mu J_z\\ \frac{1}{\rho }\frac{d}{d\rho }\left(\rho \frac{d{J}_z}{d\rho }\right)+\mu \omega \sigma \left(\frac{\epsilon \omega }{\sigma }+i\right)J_z=0\\ {\rho }^2\frac{d^2{J}_z}{d{\rho }^2}+\rho \frac{d{J}_z}{d\rho }+2\left(i+\gamma \right){\left(\frac{\rho }{\delta }\right)}^2{J}_z=\mathrm{0,}\{\begin{array}{l}\delta =\sqrt{\frac{2}{\mu \sigma \omega }}\\ \gamma =\frac{\epsilon \omega }{\sigma }\end{array}\end{array}}$

Introduciendo el parámetro adimensional r

${\displaystyle \begin{array}{l}r=\sqrt{2\left(i+\gamma \right)}\frac{\rho }{\delta }\\ r^2\frac{d^2{J}_z}{d{r}^2}+r\frac{d{J}_z}{dr}+r^2{J}_z=0\end{array}}$

Esta es la ecuación diferencial de Bessel con n=0, cuya solución

${\displaystyle J_z=C{J}_0(r)+D{Y}_0(r)}$

Se descarta el segundo término, ya que Y₀(x) tiende a -∞ cuando r→0

Sabiendo que j₀ es la densidad de corriente para ρ=a

${\displaystyle \begin{array}{l}{j}_0=C{J}_0\left(\sqrt{2\left(i+\gamma \right)}\frac{a}{\delta }\right)\\ J_z\left(\rho \right)=j_0\frac{J_0\left(\sqrt{2\left(i+\gamma \right)}\frac{\rho }{\delta }\right)}{J_0\left(\sqrt{2\left(i+\gamma \right)}\frac{a}{\delta }\right)}\\ \overrightarrow{J}=j_0\frac{J_0\left(\sqrt{2\left(i+\gamma \right)}\frac{\rho }{\delta }\right)}{J_0\left(\sqrt{2\left(i+\gamma \right)}\frac{a}{\delta }\right)}\exp \left(-i\omega t\right)\widehat{k}\end{array}}$

J_z(ρ) es un número complejo que tiene un módulo y un argumento φ

${\displaystyle J_z=\left|J_z\left(\rho \right)\right|\exp \left(-i\left(\omega t+\phi \right)\right),\left|J_z\left(\rho \right)\right|=\sqrt{{\Re }^2\left(J_z\left(\rho \right)\right)+{\Im }^2\left(J_z\left(\rho \right)\right)}}$

Representamos el módulo |J_z(ρ)|/j₀ en función de ρ/a para tres casos distintos

• δ=1/5 y γ=0

delta=1/5;
gamma=0;
a=1;
f=@(x) abs(besselj(0,sqrt(2*(gamma+1i))*x/delta)/
besselj(0,sqrt(2*(gamma+1i))*a/delta));
fplot(f, [-1,1])
grid on
xlabel('\rho/a')
ylabel('|j(\rho)|/|j_0|')
title('Módulo de la densidad de corriente')



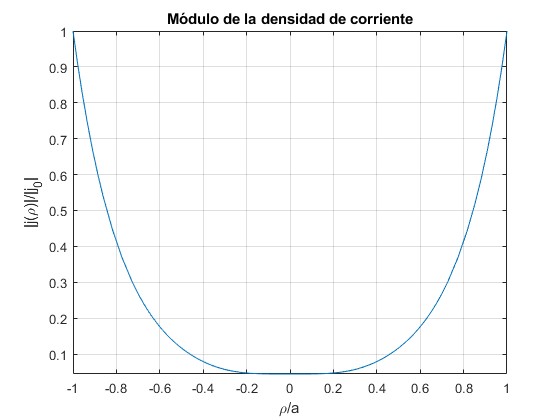
Que es similar a la obtenida en la primera parte, efecto pelicular. La densidad de corriente es mayor en la superficie del cable que en el centro

Para una frecuencia dada ω de la corriente alterna, los buenos conductores tienen una conductividad elevada σ= 5.71·10⁷ Ω^-1·m^-1 (para el cobre), por los que γ y δ son pequeños.

${\displaystyle \delta =\sqrt{\frac{2}{\mu \sigma \omega }},\gamma =\frac{\epsilon \omega }{\sigma }}$

• δ=1 y γ=2.2



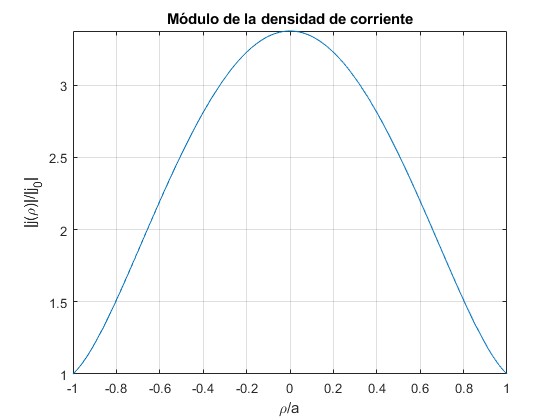
El módulo de la densidad de corriente es mayor en el centro que en la superficie del cable. Tenemos el efecto pelicular inverso

• δ=1/5 y γ=4.5



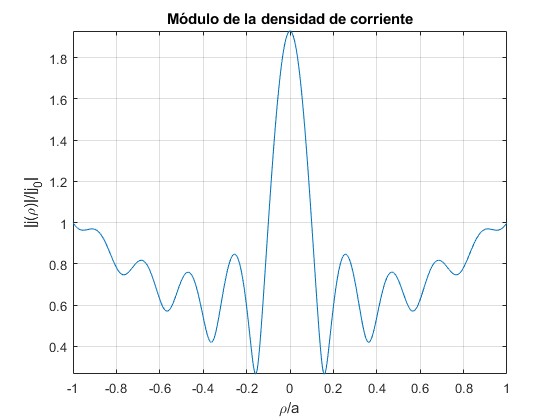
El módulo de la densidad de corriente tiene un comportamiento complejo

Representamos la parte real de la densidad de corriente en función de ρ/a

delta=1/5;
gamma=4.5;
a=1;
f=@(x) besselj(0,sqrt(2*(gamma+1i))*x/delta)/
besselj(0,sqrt(2*(gamma+1i))*a/delta);
g=@(x) real(f(x));
fplot(g, [-1,1])
grid on
xlabel('\rho/a')
ylabel('Re(J_z)')
title('Parte real')



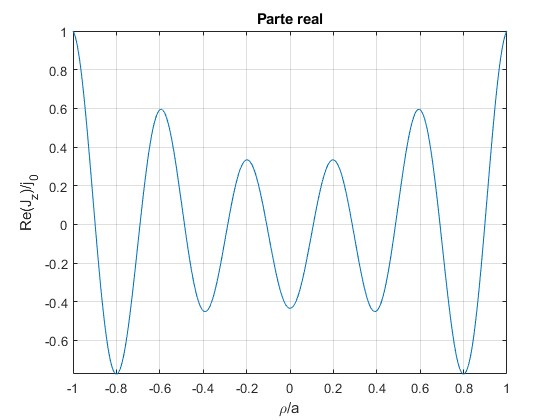
Observamos un comportamiento oscilatorio

Representamos el argumento φ en función de ρ/a para los tres casos mencionados

• δ=1/5 y γ=0

delta=1/5;
gamma=0;
a=1;
angulo=@(x) angle(besselj(0,sqrt(2*(gamma+1i))*x/delta)
/besselj(0,sqrt(2*(gamma+1i))*a/delta));
fplot(angulo, [-1,1])
grid on
set(gca,'YTick',-pi:pi/4:pi)
set(gca,'YTickLabel',{'-\pi','-3\pi/4', '-\pi/2', '-\pi/4','0',
'\pi/4','\pi/2','3\pi/4','\pi'})
xlabel('\rho/a')
ylabel('\phi')
title('Argumento de la densidad de corriente')



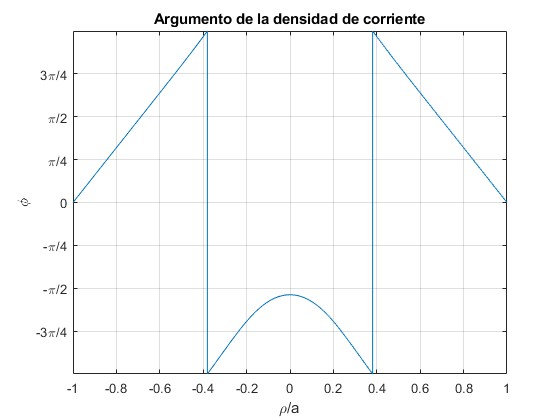
• δ=1 y γ=2.2



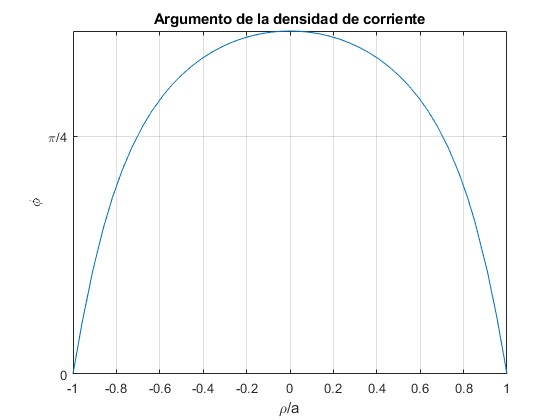
• δ=1/5 y γ=4.5

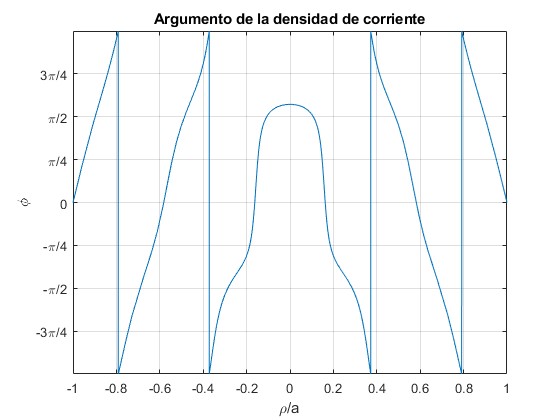
Nota: No se ha podido reproducir los casos (b) y (c) de las figuras 1 y 2 del artículo de Vladimir Ivchenko

Impedancia

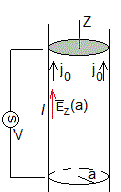
La densidad de corriente j₀ en la superficie del cable, ρ=a es

${\displaystyle V=E_z(a)l=\frac{j_0}{\sigma }l\exp (-i\omega t)}$

En el cable hay dos corrientes, la de conducción y la desplazamiento. La ley de Ampere-Maxwell es

${\displaystyle \overrightarrow{\nabla }\times \overrightarrow{B}=\mu \left(\overrightarrow{J_m}+\epsilon \frac{\partial \overrightarrow{E}}{\partial t}\right)}$

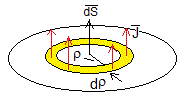
Véase la página titulada Propagación de ondas electromagnéticas. Ecuaciones de Fresnel. en el apartado 'Ecuaciones de Maxwell'. La densidad de corriente de desplazamiento es

${\displaystyle j_D=\epsilon \frac{\partial E_z}{\partial t}=-i\frac{\omega \epsilon }{\sigma }{j}_z(\rho )=-i\gamma j_z(\rho )}$

La intensidad de la corriente que circula por el cable de radio a es

${\displaystyle \begin{array}{l}I={\displaystyle \underset{0}{\overset{a}{\int }}\left(j_D+j_z\right)}\left(2\pi \rho ·d\rho \right)=\left(-i\gamma +1\right){\displaystyle \underset{0}{\overset{a}{\int }}{j}_z(\rho )}\left(2\pi \rho ·d\rho \right)=\\ \left(-i\gamma +1\right)\exp (-i\omega t){\displaystyle \underset{0}{\overset{a}{\int }}{j}_0\frac{J_0\left(\sqrt{2\left(i+\gamma \right)}\frac{\rho }{\delta }\right)}{J_0\left(\sqrt{2\left(i+\gamma \right)}\frac{a}{\delta }\right)}}\left(2\pi \rho ·d\rho \right)=\\ j_0\frac{\left(-i\gamma +1\right)\exp (-i\omega t)}{J_0\left(\sqrt{2\left(i+\gamma \right)}\frac{a}{\delta }\right)}2\pi {\displaystyle \underset{0}{\overset{a}{\int }}{J}_0\left(\sqrt{2\left(i+\gamma \right)}\frac{\rho }{\delta }\right)}\rho ·d\rho \end{array}}$

Teniendo en cuenta la propiedad de la función de Bessel

${\displaystyle {\displaystyle \underset{0}{\overset{1}{\int }}x{J}_0(kx)·dx=\frac{1}{k}}{J}_1(k)}$

El resultado es

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{a}{\int }}{J}_0\left(\sqrt{2\left(i+\gamma \right)}\frac{\rho }{\delta }\right)}\rho ·d\rho =a^2{\displaystyle \underset{0}{\overset{1}{\int }}{J}_0\left(\sqrt{2\left(i+\gamma \right)}\frac{a}{\delta }x\right)}x·dx=\frac{a^2}{\sqrt{2\left(i+\gamma \right)}\frac{a}{\delta }}{J}_1\left(\sqrt{2\left(i+\gamma \right)}\frac{a}{\delta }\right)\\ I=2\pi j_0\left(-i\gamma +1\right)\frac{\delta a}{\sqrt{2\left(i+\gamma \right)}}\frac{J_1\left(\sqrt{2\left(i+\gamma \right)}\frac{a}{\delta }\right)}{J_0\left(\sqrt{2\left(i+\gamma \right)}\frac{a}{\delta }\right)}\exp (-i\omega t)\end{array}}$

La impedancia es

${\displaystyle \begin{array}{l}Z\left(\omega \right)=\frac{V}{I}=\frac{\frac{j_0}{\sigma }l}{2\pi j_0\left(-i\gamma +1\right)\frac{\delta a}{\sqrt{2\left(i+\gamma \right)}}\frac{J_1\left(\sqrt{2\left(i+\gamma \right)}\frac{a}{\delta }\right)}{J_0\left(\sqrt{2\left(i+\gamma \right)}\frac{a}{\delta }\right)}}=\\ Z\left(\omega \right)=\frac{R_0}{2}\frac{\sqrt{2\left(i+\gamma \right)}a}{\left(-i\gamma +1\right)\delta }\frac{J_0\left(\sqrt{2\left(i+\gamma \right)}\frac{a}{\delta }\right)}{J_1\left(\sqrt{2\left(i+\gamma \right)}\frac{a}{\delta }\right)},R_0=\frac{1}{\sigma }\frac{l}{\pi a^2}\end{array}}$

R₀ es la resistencia de una porción l de cable de radio a para ω=0

Cuando circula una corriente alterna, I(t)=I₀exp(iωt), de frecuencia angular ω, la impedancia Z del conductor es

${\displaystyle Z=Z_R+Z_L=R-\text{i}\omega L}$

Siendo L el coeficiente de autoinducción de la porción l del conductor

Representamos la parte real R de Z(ω) en función de a/δ para δ=1/5 y γ=0

delta=1/5;
gamma=0;
f=@(x) sqrt(2*(1i+gamma))*besselj(0,sqrt(2*(gamma+1i))*x).*x./
(2*besselj(1,sqrt(2*(gamma+1i))*x)*(1-gamma*1i));
g=@(x) real(f(x));
fplot(g, [0,5])
grid on
xlabel('a/\delta')
ylabel('Re(Z)/R_0')
title('Parte real')

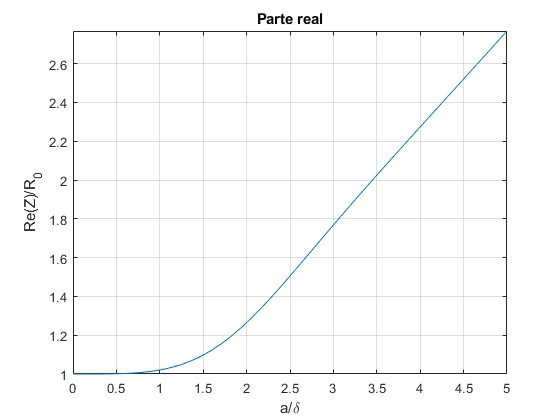
La gráfica es similar a la que se ha obtenido en la primera parte de esta página

Representamos ωL, la parte imaginaria de Z(ω) en función de a/δ

delta=1/5;
gamma=0;
f=@(x) sqrt(2*(1i+gamma))*besselj(0,sqrt(2*(gamma+1i))*x).*x./
(2*besselj(1,sqrt(2*(gamma+1i))*x)*(1-gamma*1i));
g=@(x) imag(f(x));
fplot(g, [0,5])
grid on
xlabel('a/\delta')
ylabel('Imag(Z)/R_0')
title('Parte imaginaria')

La gráfica es similar a la que se ha obtenido en la primera parte de esta página

Representamos |Z(ω)| en función de la frecuencia f para dos valores del radio a, 1 mm y 0.5 mm

function skin_8
   epsilon=0;
   sigma=5.9e7;%conductividad del cobre
   hold on
   a=0.001;
   g=@(x) abs(f(a,x));
   fplot(g, [0,250])
   a=0.0005;
   g=@(x) abs(f(a,x));
    fplot(g, [0,250])
    hold off
    grid on
    legend('1 mm','0.5 mm','location', 'best')
    xlabel('f (kHz)')
    ylabel('|Z|/R_0')
    title('Valor absoluto')
    
    function res=f(a,x)
        gamma=epsilon*2*pi*x*1e3/sigma; %frecuencia en kHz
        delta=sqrt(2./(8*pi^2*1e-7*sigma*x*1e3)); %frecuencia en kHz
        res=sqrt(2*(1i+gamma)).*besselj(0,sqrt(2*(gamma+1i))*a./delta)*a.
/(2*delta.*besselj(1,sqrt(2*(gamma+1i))*a./delta).*(1-gamma*1i));
    end
end  

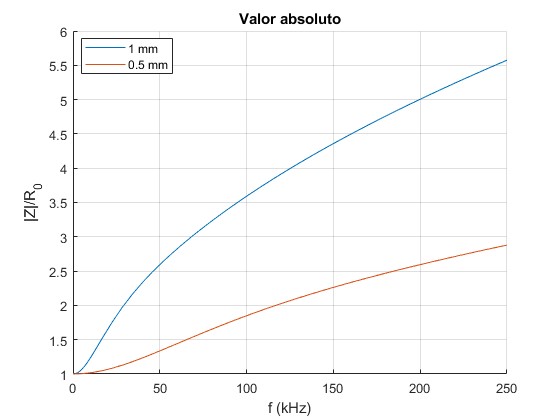
Representamos la parte real e imaginaria de la impedancia Z(ω) de un cable de cobre de radio a=1 cm en función de la frecuencia f en el intervalos [0, 0.3] kHz

function skin_9
    epsilon=0; %permitividad eléctrica
    sigma=5.9e7; %conductividad del cobre
    a=0.01; %radio
    hold on
    g=@(x) real(f(x));
    fplot(g, [0,0.3])
    g=@(x) abs(imag(f(x)));
    fplot(g, [0,0.3])
    hold off
    grid on
    xlabel('f (kHz)')
    ylabel('Z/R_0')
    legend('real','imaginaria','location','best')
    title('Real e imaginaria')
    
    function res=f(x)
        gamma=epsilon*2*pi*x*1e3/sigma; %frecuencia en kHz
        delta=sqrt(2./(8*pi^2*1e-7*sigma*x*1e3)); %frecuencia en kHz
        res=sqrt(2*(1i+gamma)).*besselj(0,sqrt(2*(gamma+1i))*a./delta)*a.
/(2*delta.*besselj(1,sqrt(2*(gamma+1i))*a./delta).*(1-gamma*1i));
    end
end

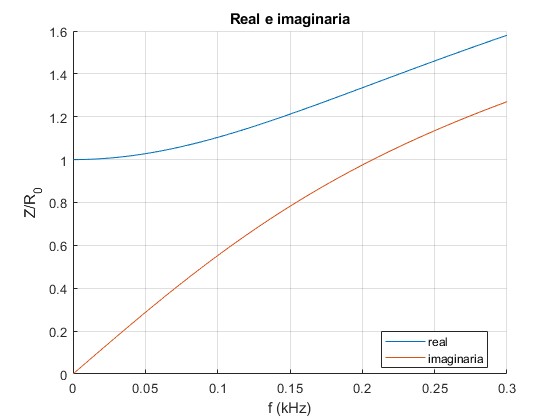
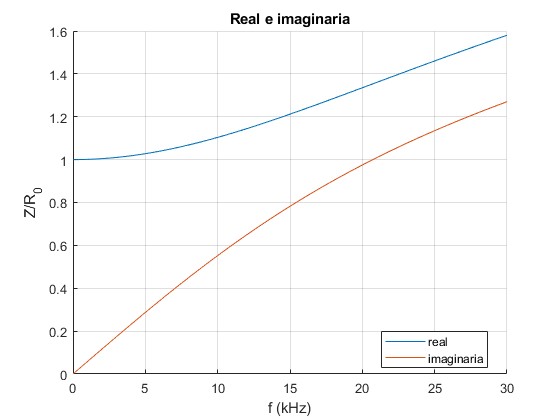
Representamos la parte real e imaginaria de la impedancia Z(ω) de un cable de cobre de radio a=1 mm en función de la frecuencia f en el intervalos [0, 30] kHz

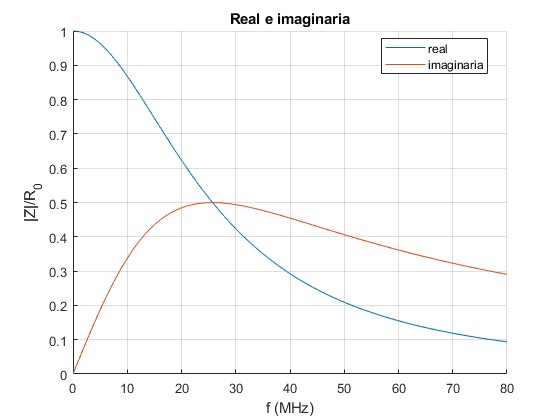
Representamos la parte real e imaginaria de la impedancia Z(ω) de un cable de radio a=1 cm, hecho de un material de conductividad σ=0.1 Ω^-1·m^-1, permitividad eléctrica relativa ε_r=70, en función de la frecuencia f en el intervalos [0, 80] MHz

function skin_11
    epsilon=70/(4*pi*9e9); %permitividad eléctrica 
    sigma=0.1; %conductividad
    a=0.01; %radio
    hold on
    g=@(x) real(f(x));
    fplot(g, [0,80])
    g=@(x) abs(imag(f(x)));
    fplot(g, [0,80])
    hold off
    grid on
    legend('real','imaginaria','location','best')
    xlabel('f (MHz)')
    ylabel('|Z|/R_0')
    title('Real e imaginaria')

    function res=f(x)
        gamma=epsilon*2*pi*x*1e6/sigma; %frecuencia en MHz
        delta=sqrt(2./(8*pi^2*1e-7*sigma*x*1e6)); %frecuencia en MHz
        res=sqrt(2*(1i+gamma)).*besselj(0,sqrt(2*(gamma+1i))*a./delta)*a./
(2*delta.*besselj(1,sqrt(2*(gamma+1i))*a./delta).*(1-gamma*1i));
    end
end

Referencias

Glenn S Smith. A simple derivation for the skin effect in a round wire. Eur. J. Phys. 35 (2014) 025002

Vladimir Ivchenko. The inverse skin effect in a weakly conducting medium. Revista Brasileira de Ensino de Física, vol. 47, e20240423 (2025)