En primer lugar, analizaremos un caso sencillo, aunque irreal, que nos va a dar una idea del comportamiento de la gota que cae. Supongamos que, a medida que la gota de radio r cae en una atmósfera cuyo vapor se condensa, incrementa su masa m en proporción a su superficie 4πr²

${\displaystyle \frac{dm}{dt}=c\rho 4\pi r^2}$

Calculamos la masa y el radio de la gota en función del tiempo t

${\displaystyle \begin{array}{l}m=\rho \frac{4}{3}\pi r^3\\ \frac{dm}{dt}=\frac{dm}{dr}\frac{dr}{dt}=\rho 4\pi r^2\frac{dr}{dt}\end{array}}$

Despejamos dr/dt

${\displaystyle \begin{array}{l}\frac{dr}{dt}=c\\ r=ct+C\\ r=R+ct=R(1+kt)\\ m=\rho \frac{4}{3}\pi R^3{\left(1+kt\right)}^3=\rho \frac{4}{3}\pi R^3{\left(1+kt\right)}^3\end{array}}$

Hemos supuesto que en el instante t=0, el radio de la gota es R

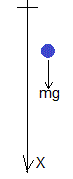
La ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d(mv)}{dt}=mg\\ \frac{d}{dt}\left(\rho \frac{4}{3}\pi R^3{\left(1+kt\right)}^{3}v\right)=\rho \frac{4}{3}\pi R^3{\left(1+kt\right)}^{3}g\end{array}}$

Simplificamos los términos constantes, e integramos el segundo miembro respecto de t, para obtener la velocidad v de la gota en función del tiempo, teniendo en cuenta que en el instante t=0, parte del reposo, v=0

${\displaystyle \begin{array}{l}{\left(1+kt\right)}^{3}v=\frac{1}{4k}{\left(1+kt\right)}^{4}g+C\\ C=-\frac{1}{4k}g\\ 4k{\left(1+kt\right)}^{3}v={\left(1+kt\right)}^{4}g-g\\ v=\frac{g}{4k}\left(1+kt-\frac{1}{{\left(1+kt\right)}^3}\right)\end{array}}$

hold on
for k=[0.1,0.5,1,1.5]
    f=@(t) (1+k*t-1./(1+k*t).^3)*9.8/(4*k);
    fplot(f,[0,10],'displayName',num2str(k))
end
hold off
legend('-DynamicLegend','location','northwest')
grid on
xlabel('t')
ylabel('v')
title('Caída de una gota')

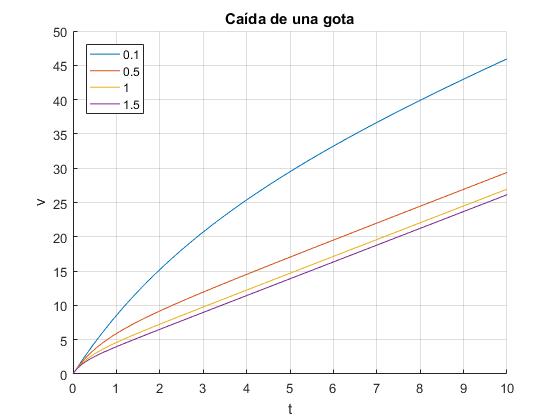
Cuando t se hace grande, la velocidad crece linealmente con t con pendiente g/4, como apreciamos en la gráfica. Derivando la velocidad v con respecto del tiempo t, comprobamos que la aceleración a tiende hacia el valor constante g/4

La masa de la gota

Hemos de hacer una suposición acerca de la forma en que la masa de la gota se incrementa con el tiempo. Si la gota va absorbiendo las pequeñas gotitas que encuentra en su camino, entonces

${\displaystyle \frac{dm}{dt}\propto (\text{área)}\times \text{(velocidad})\propto \pi r^{2}v={\rho }_n\pi r^{2}v=k{m}^{2/3}v}$

• πr² es el área trasversal de la gota supuesta esférica
• ρ_n es la densidad de la niebla,
• v es la velocidad de la gota

• m es la masa de la gota, y ρ_a es la densidad del agua, m=densidad·volumen=ρ_a·(4/3)πr³

El valor de la constante de proporcionalidad k es

${\displaystyle k=\frac{{\rho }_n\pi }{{\left({\rho }_a\frac{4}{3}\pi \right)}^{2/3}}}$

En general, supondremos que la razón del incremento de la masa de la gota con el tiempo es de la forma, con α=2/3

${\displaystyle \frac{dm}{dt}=k{m}^{\alpha }v}$

Como la velocidad v=dx/dt

${\displaystyle \frac{dm}{dt}=k{m}^{\alpha }\frac{dx}{dt}}$

Integramos esta ecuación con las condiciones iniciales para x=0, m=m₀

${\displaystyle \begin{array}{l}{\displaystyle \underset{m_0}{\overset{m}{\int }}{m}^{-\alpha }}dm={\displaystyle \underset{0}{\overset{x}{\int }}k·dx}\\ m^{1-\alpha }-m_0^{1-\alpha }=(1-\alpha )kx\\ m={\left((1-\alpha )kx+m_0^{1-\alpha }\right)}^{1/(1-\alpha )}\end{array}}$

Esta ecuación nos proporciona la masa m de la gota en función de la posición x.

Ecuaciones del movimiento

Supondremos que sobre la gota de masa m actúa una única fuerza que es su peso mg. La segunda ley de Newton aplicada a este sistema de masa variable se escribe

${\displaystyle \frac{d(mv)}{dt}=mgm\frac{dv}{dt}+v\frac{dm}{dt}=mg}$

Cuando g=0

Empezaremos por el caso más simple, aquél en el que la aceleración de la gravedad es cero. Podría ser el caso de un objeto que pasase a través de la materia interestelar.

Como la fuerza exterior es nula, el momento lineal se conserva, al aumentar la masa disminuye la velocidad de la gota

m₀v₀=mv

${\displaystyle \frac{dx}{dt}=\frac{m_0{v}_0}{m}=\frac{m_0{v}_0}{{\left((1-\alpha )kx+m_0^{1-\alpha }\right)}^{1/(1-\alpha )}}}$

Integramos

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{x}{\int }}{\left((1-\alpha )kx+m_0^{1-\alpha }\right)}^{1/(1-\alpha )}}dx={\displaystyle \underset{0}{\overset{t}{\int }}{m}_0{v}_{0}dt}\\ \frac{1}{k(2-\alpha )}\left\{{\left((1-\alpha )kx+m_0^{1-\alpha }\right)}^{(2-\alpha )/(1-\alpha )}-m_0^{(2-\alpha )}\right\}=m_0{v}_{0}t\end{array}}$

Expresamos x en función del tiempo t

${\displaystyle x=\frac{1}{k(1-\alpha )m_0^{(-1+\alpha )}}\left\{{\left(k(2-\alpha )m_0^{(-1+\alpha )}{v}_{0}t+1\right)}^{(1-\alpha )/(2-\alpha )}-1\right\}}$

Calculamos ahora la velocidad v en función del tiempo t

${\displaystyle v=\frac{m_0{v}_0}{m}=\frac{m_0{v}_0}{{\left((1-\alpha )kx+m_0^{1-\alpha }\right)}^{1/(1-\alpha )}}=\frac{v_0}{{\left(k(2-\alpha )m_0^{(-1+\alpha )}{v}_{0}t+1\right)}^{1/(2-\alpha )}}}$

Integrando de nuevo, obtenemos la posición x de la gota en función del tiempo t.

$$\begin{gathered} {\displaystyle x={\displaystyle \underset{0}{\overset{t}{\int }}\frac{v_0}{{\left(k(2-\alpha )m_0^{(-1+\alpha )}{v}_{0}t+1\right)}^{1/(2-\alpha )}}dt}= \\ \frac{1}{k(1-\alpha )m_0^{(-1+\alpha )}}\left\{{\left(k(2-\alpha )m_0^{(-1+\alpha )}{v}_{0}t+1\right)}^{(1-\alpha )/(2-\alpha )}-1\right\}} \end{gathered}$$

Cuando α=2/3 las expresiones de la masa m de la gota, la velocidad v y la posición x en función del tiempo t son:

${\displaystyle \begin{array}{l}m={\left(\frac{1}{3}kx+m_0^{1/3}\right)}^3\\ v=\frac{v_0}{{\left(\frac{4}{3}k{m}_0^{-1/3}{v}_{0}t+1\right)}^{3/4}}x=\frac{3m_0^{1/3}}{k}\left\{{\left(\frac{4}{3}k{m}_0^{-1/3}{v}_{0}t+1\right)}^{1/4}-1\right\}\end{array}}$

Cuando g≠0

Resolveremos por procedimientos numéricos, las ecuaciones

${\displaystyle \begin{array}{l}\frac{dm}{dt}=k{m}^{\alpha }v\\ m\frac{dv}{dt}+v\frac{dm}{dt}=mg\end{array}}$

Antes, vamos a comprobar que la aceleración dv/dt tiende hacia un valor límite constante.

Eliminado la derivada de m en las dos ecuaciones que describen el movimiento de la gota, obtenemos una ecuación diferencial de primer orden en v.

${\displaystyle \begin{array}{l}\frac{dm}{dt}=k{m}^{\alpha }v\\ \frac{dv}{dt}+k{m}^{\alpha -1}{v}^2=g{m}^{-\alpha +1}=k\frac{v^2}{g-dv/dt}\end{array}}$

Derivamos respecto del tiempo

${\displaystyle (-\alpha +1)m^{-\alpha }\frac{dm}{dt}=k\frac{2v\frac{dv}{dt}\left(g-\frac{dv}{dt}\right)-v^2\left(-\frac{d^{2}v}{d{t}^2}\right)}{{\left(g-\frac{dv}{dt}\right)}^2}}$

Sustituyendo dm/dt=km^αv

${\displaystyle \frac{d^{2}v}{d{t}^2}=\frac{\left(g-dv/dt\right)}{v}\left((1-\alpha )g-(3-\alpha )\frac{dv}{dt}\right)}$

La aceleración es constante cuando el término entre paréntesis es cero

${\displaystyle \frac{dv}{dt}=\frac{1-\alpha }{3-\alpha }g}$

Cuando α=2/3, la aceleración es constante e igual a 1/7 de la aceleración de la gravedad g

${\displaystyle \frac{dv}{dt}=\frac{1}{7}g}$

Procedimiento numérico

Ya hemos integrado la primera ecuación, obteniendo la expresión de la masa m de la gota en función del desplazamiento x

${\displaystyle m^{1-\alpha }=m_0^{1-\alpha }+\left(1-\alpha \right)k·x}$

La segunda ecuación se escribe

${\displaystyle \begin{array}{l}m\frac{dv}{dt}+v\frac{dm}{dt}=mg\\ \frac{dv}{dt}=g-\frac{k{v}^2}{m^{1-\alpha }}\\ \frac{d^{2}x}{d{t}^2}=g-\frac{k{\left(dx/dt\right)}^2}{m_0^{1-\alpha }+(1-\alpha )k·x}\end{array}}$

Se resuelve esta ecuación diferencial por procedimientos numéricos, tomando α=2/3, con las condiciones iniciales: t=0, dx/dt=0, x=0

La masa inicial m₀ en gramos es el producto de la densidad del agua 1.0 g/cm³ por el volumen de una esfera de radio r₀ en cm

${\displaystyle m_0=\frac{4}{3}\pi r_0^3}$

El valor de la constante de proporcionalidad k es

${\displaystyle k=\frac{{\rho }_n\pi }{{\left({\rho }_a\frac{4}{3}\pi \right)}^{2/3}}=\frac{{10}^{-6}\pi }{{\left(\frac{4}{3}\pi \right)}^{2/3}}=1.21·{10}^{-5}}$

Donde ρ_n≈10^-3 kg/m³ es la densidad de la niebla, y ρ_a=1000 kg/m³ es la densidad del agua. La constante de proporcionalidad k es por tanto, del orden de 10^-5. La aceleración de la gravedad es g=9.81 m/s².

alfa=2/3;
r0=0.0001;  %radio de la gota en m
k=1e-5; %parámetro
m0=1000*4*pi*r0*r0*r0/3;
x0=[0,0];  %condiciones iniciales
f=@(t,x) [x(2); 9.81-k*x(2)^2/(m0^(1-alfa)+k*x(1)*(1-alfa))]; 
tspan=[0 30];
[t,x]=ode45(f,tspan,x0);
acel=@(x,v) 9.81-(k*v.^2)./(m0^(1-alfa)+k*x*(1-alfa)); %aceleración
plot(t,acel(x(:,1),x(:,2)))
grid on
xlabel('t(s)')
ylabel('a(m/s^2)');
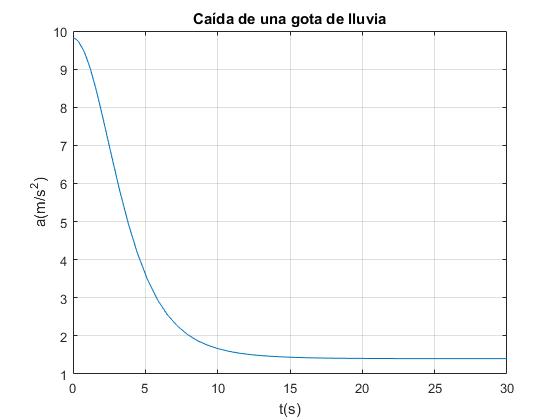
title('Caída de una gota de lluvia')

Actividades

Se introduce

• El radio inicial r₀ de la gota en mm, en el control titulado Radio

• La constante de proporcionalidad k en el intervalo 0.1·10^-5 a 9.0·10^-5, en el control titulado Parámetro k.

Se pulsa el botón titulado Nuevo

Se observa la caída de la gota de agua en la parte izquierda

Se representa la aceleración dv/dt de la gota en función del tiempo t, observando que tiende hacia el valor límite g/7=1.4 m/s².

Vemos como la gota cambia su tamaño a medida que absorbe las pequeñas gotas suspendidas en el aire y que forman la niebla.

El problema general

Las ecuaciones que describen el movimiento de la gota son:

${\displaystyle \begin{array}{l}\frac{dm}{dt}=k{m}^{\alpha }{v}^{\beta }\\ \frac{dp}{dt}=mg\end{array}}$

donde k>0, 1>α≥0, β≥0.

Dividiendo la segunda entre las primera

${\displaystyle \begin{array}{l}{p}^{\beta }dp=\frac{g}{k}{m}^{1-\alpha +\beta }dm\\ \frac{p^{\beta }}{\beta +1}=\frac{g}{k}\frac{m^{2-\alpha +\beta }}{2-\alpha +\beta }+c\end{array}}$

Despejamos la velocidad v teniendo en cuenta que el momento lineal p=mv.

${\displaystyle v=\frac{g}{k}\left(\frac{\beta +1}{2+\beta -\alpha }\right)m^{1-\alpha }+\frac{c}{m^{\beta +1}}}$

Donde c es una constante de integración que se determina a partir de las condiciones iniciales, para m=m₀, v=0, la gota parte del reposo con una masa inicial m₀.

${\displaystyle v={\left(\frac{g}{k}\frac{\beta +1}{2+\beta -\alpha }\right)}^{1/(1+\beta )}{\left(1-{\left(\frac{m_0}{m}\right)}^{2+\beta -\alpha }\right)}^{1/(1+\beta )}{m}^{(1-\alpha )/(1+\beta )}}$

Para obtener la masa en función del tiempo, introducimos la expresión de v en la ecuación dm/dt=k·m^α·v^β

${\displaystyle {\displaystyle \underset{m_0}{\overset{m}{\int }}{m}^{-(\alpha +\beta )/(1+\beta )}{\left(1-{\left(\frac{m_0}{m}\right)}^{2+\beta -\alpha }\right)}^{-\beta /(1+\beta )}dm=}k{\left(\frac{g}{k}\frac{\beta +1}{2+\beta -\alpha }\right)}^{\beta /(1+\beta )}t}$

Después de hacer el cambio de variable z=(m₀/m)²+β-α, la integral se expresa en términos de la función especial beta.

Aceleración de la gota

Partimos de las ecuaciones del movimiento de la gota

${\displaystyle \begin{array}{l}\frac{dm}{dt}=k{m}^{\alpha }{v}^{\beta }\\ m\frac{dv}{dt}+v\frac{dm}{dt}=mg\end{array}}$

Introducimos la primera en la segunda, y despejamos la masa m

${\displaystyle m^{1-\alpha }=k\frac{v^{\beta +1}}{g-dv/dt}}$

Derivamos con respecto del tiempo

${\displaystyle \left(1-\alpha \right)m^{-\alpha }\frac{dm}{dt}=k\frac{\left(\beta +1\right)v^{\beta }\left(\frac{dv}{dt}\right)\left(g-\frac{dv}{dt}\right)+v^{\beta +1}\frac{d^{2}v}{d{t}^2}}{{\left(g-\frac{dv}{dt}\right)}^2}}$

Sustituimos dm/dt=k·m^α·v^β

${\displaystyle \frac{d^{2}v}{d{t}^2}=\frac{g-dv/dt}{v}\left(g(1-\alpha )-\left(2+\beta -\alpha \right)\frac{dv}{dt}\right)}$

La aceleración es constante cuando el término entre paréntesis es nulo

${\displaystyle \frac{dv}{dt}=\frac{(1-\alpha )}{2+\beta -\alpha }g}$

• Para β=1 y α=2/3, la aceleración tiende a g/7
• Para β=0 y α=2/3, la aceleración tiende a g/4

Casos particulares

En esta sección vamos a estudiar estos dos casos

La masa m de una gota supuesta esférica de radio r es

${\displaystyle m=\rho \frac{4}{3}\pi r^3}$

La ecuación que describe la variación de la masa con el tiempo dm/dt=k·m^αv^β, se escribe en términos del radio r de la gota

${\displaystyle \frac{dr}{dt}=\gamma r^{3\alpha -2}{v}^{\beta }\gamma =\frac{k}{3}{\left(\frac{4\rho \pi }{3}\right)}^{\alpha -1}}$

La ecuación del movimiento se escribe

${\displaystyle \begin{array}{l}\frac{dv}{dt}=g-v\frac{dm}{dt}\frac{1}{m}\\ \frac{dv}{dt}=g-3\gamma r^{3\alpha -3}{v}^{\beta +1}\end{array}}$

α=2/3, β=0

El sistema de dos ecuaciones diferenciales se convierte en otro más sencillo

${\displaystyle \begin{array}{l}\frac{dr}{dt}=\gamma \\ \frac{dv}{dt}=g-3\gamma \frac{v}{r}\end{array}}$

Convertimos las dos ecuaciones diferenciales en una única ecuación diferencial en dv/dr, para determinar la velocidad de la gota en función del radio

${\displaystyle \begin{array}{l}\frac{dv}{dt}=\frac{dv}{dr}\frac{dr}{dt}\\ \frac{dv}{dr}=\frac{g}{\gamma }-3\frac{v}{r}\end{array}}$

Resolvemos esta la ecuación diferencial con las condiciones iniciales, cuando r=r₀, v=0. Se trata de una ecuación diferencial de la forma

${\displaystyle \frac{dy}{dx}+3\frac{y}{x}=a}$

Hacemos el cambio y=u·v

${\displaystyle \begin{array}{l}u\frac{dv}{dx}+\frac{du}{dx}v+3\frac{uv}{x}=a\\ v\left(\frac{du}{dx}+3\frac{u}{x}\right)+u\frac{dv}{dx}=a\end{array}}$

La solución de u es

${\displaystyle \begin{array}{l}\frac{du}{dx}+3\frac{u}{x}=0\\ \frac{du}{u}=-3\frac{dx}{x}\\ \ln u=-3\ln xu=\frac{1}{x^3}\end{array}}$

La solución de v es

${\displaystyle \begin{array}{l}\frac{1}{x^3}\frac{dv}{dx}=a\\ v=a\frac{x^4}{4}+C\end{array}}$

Solución completa y=u·v es

${\displaystyle y=\frac{1}{x^3}\left(a\frac{x^4}{4}+C\right)}$

Retornamos a las variables r=x, v=y, a=g/γ

${\displaystyle v=\frac{1}{r^3}\left(\frac{g}{\gamma }\frac{r^4}{4}+C\right)}$

La constante C se determina a partir de las condiciones iniciales , para r=r₀, v=0;

${\displaystyle v=\frac{g}{4\gamma }\left(r-\frac{r_0^4}{r^3}\right)}$

Resolvemos aplicando procedimientos numéricos, el sistema de dos ecuaciones diferenciales, tomando α=2/3, y β=0.

beta=0;
r0=0.0001;
gamma=2.5e-7;
%x(1) es la velocidad, x(2) es el radio de la gota
f=@(t,x) [9.81-3*gamma*x(2)^(3*alfa-3)*x(1)^(beta+1); 
gamma*x(2)^(3*alfa-2)*x(1)^beta];
[t,x]=ode45(f,[0,300],[0,r0]);
subplot(1,2,1)
plot(t,x(:,2)*1000)
grid on
xlabel('t (s)')
ylabel('r (mm)')
subplot(1,2,2)
plot(t,x(:,1))
grid on
xlabel('t (s)')
ylabel('v(m/s)')
figure
hold on
plot(x(:,2)*1000,x(:,1)) %numérico
%Expresión de la velocidad en función del radio
v=@(r) 9.81*r.*(1-(r0*1000./r).^4)/(4*gamma*1000);
fplot(v,[r0,x(end,2)]*1000)
hold off
legend('numérico','exacto','location','northwest')
grid on
ylabel('v (m/s)')
xlabel('r (mm)')
title('Gota que cae')

Representamos el radio r y la velocidad v de la gota en función del tiempo

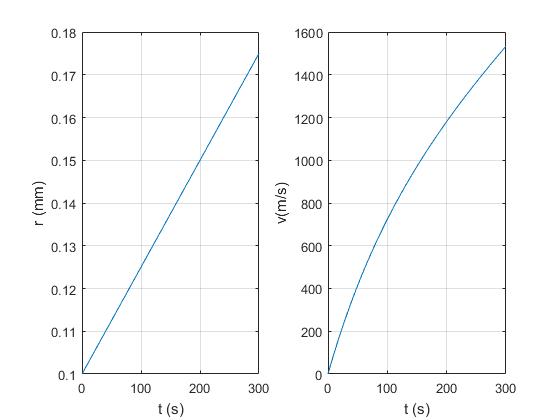
El radio r crece linealmente con el tiempo t

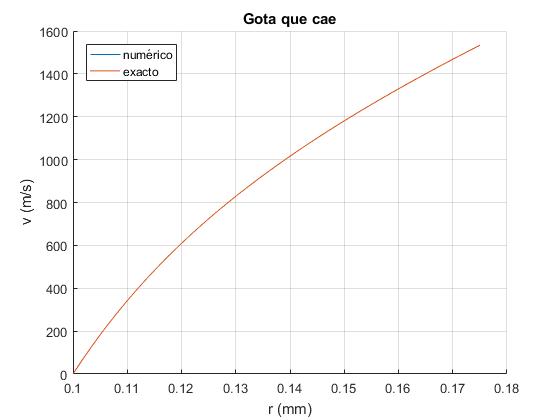
Representamos la velocidad de la gota v en función de su radio r. Vemos que la solución numérica coincide con la expresión analítica que hemos obtenido de la velocidad en función del radio v(r). Cuando r se hace grande, la velocidad v crece linealmente con r

α=2/3, β=1

El sistema de dos ecuaciones diferenciales se convierte en otro más sencillo

${\displaystyle \{\begin{array}{l}\frac{dv}{dt}=g-3\gamma \frac{v^2}{r}\\ \frac{dr}{dt}=\gamma v\end{array}}$

Convertimos las dos ecuaciones diferenciales en una única ecuación diferencial en dv/dr, para determinar la velocidad de la gota en función del radio

${\displaystyle \begin{array}{l}\frac{dv}{dt}=\frac{dv}{dr}\frac{dr}{dt}\\ \frac{dv}{dr}=\frac{g}{\gamma v}-3\frac{v}{r}\end{array}}$

Resolvemos esta la ecuación diferencial con las condiciones iniciales, cuando r=r₀, v=0. Se trata de una ecuación diferencial de la forma

${\displaystyle \frac{dy}{dx}+3\frac{y}{x}=\frac{a}{y}}$

Multiplicando por y

${\displaystyle y\frac{dy}{dx}+3\frac{y^2}{x}=a}$

Haciendo el cambio de variable,

${\displaystyle z=y^2\frac{dz}{dx}=2y\frac{dy}{dx}}$

La ecuación diferencial se convierte en

${\displaystyle \frac{1}{2}\frac{dz}{dx}+3\frac{z}{x}=a}$

Sea z=u·v

${\displaystyle \begin{array}{l}\frac{1}{2}\left(u\frac{dv}{dx}+\frac{du}{dx}v\right)+3\frac{u·v}{x}=a\\ v\left(\frac{1}{2}\frac{du}{dx}+3\frac{u}{x}\right)+\frac{1}{2}u\frac{dv}{dx}=a\end{array}}$

La solución de u es

${\displaystyle \begin{array}{l}\frac{1}{2}\frac{du}{dx}+3\frac{u}{x}=0\\ \frac{du}{u}=-6\frac{dx}{x}\\ \ln u=-6\ln xu=\frac{1}{x^6}\end{array}}$

La solución de v es

${\displaystyle \begin{array}{l}\frac{1}{2}\frac{1}{x^6}\frac{dv}{dx}=a\\ v=\frac{2}{7}a{x}^7+C\end{array}}$

La solución completa y²=u·v es,

${\displaystyle y^2=\frac{1}{x^6}\left(\frac{2}{7}a{x}^7+C\right)}$

Retornando las variables r=x, v=y, a=g/γ

${\displaystyle v^2=\frac{1}{r^6}\left(\frac{2}{7}\frac{g}{\gamma }{r}^7+C\right)}$

La constante C se determina a partir de las condiciones iniciales, para r=r₀, v=0;

${\displaystyle v=\sqrt{\frac{2}{7}\frac{g}{\gamma }\left(r-\frac{r_0^7}{r^6}\right)}}$

Resolvemos aplicando procedimientos numéricos, el sistema de dos ecuaciones diferenciales, tomando α=2/3, y β=1.

alfa=2/3;
beta=1;
r0=0.0001;
gamma=2.5e-7;
%x(1) es la velocidad, x(2) es el radio de la gota
f=@(t,x) [9.81-3*gamma*x(2)^(3*alfa-3)*x(1)^(beta+1);
 gamma*x(2)^(3*alfa-2)*x(1)^beta];
[t,x]=ode45(f,[0,300],[0,r0]);
subplot(1,2,1)
plot(t,x(:,2)*1000)
grid on
xlabel('t (s)')
ylabel('r (mm)')
subplot(1,2,2)
plot(t,x(:,1))
grid on
xlabel('t (s)')
ylabel('v(m/s)')
figure
hold on
v=@(r) sqrt(2*9.81*r.*(1-(r0*1000./r).^7)/(7*gamma*1000));
plot(x(:,2)*1000,x(:,1))
fplot(v,[r0,x(end,2)]*1000)
hold off
legend('numérico','exacto','location','northwest')
grid on
ylabel('v (m/s)')
xlabel('r (mm)')
title('Gota que cae')

Utilizando Data cursor, en la gráfica de la velocidad (derecha), medimos las coordenadas de dos puntos separados (99.55, 169.6) y (202.2,314.4). Calculamos la pendiente m de la recta

${\displaystyle m=\frac{313.4-169.6}{202.2-99.5}=1.4}$

que es g/7 la aceleración límite constante que alcanza la gota de lluvia

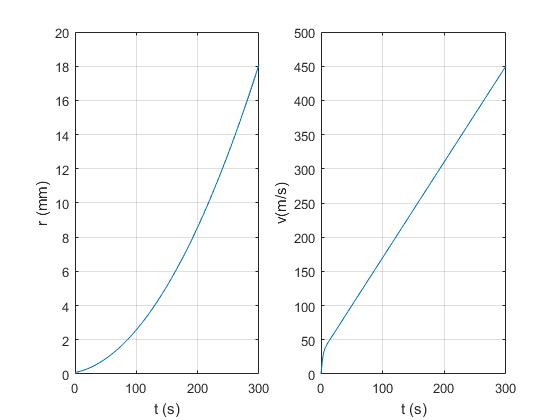
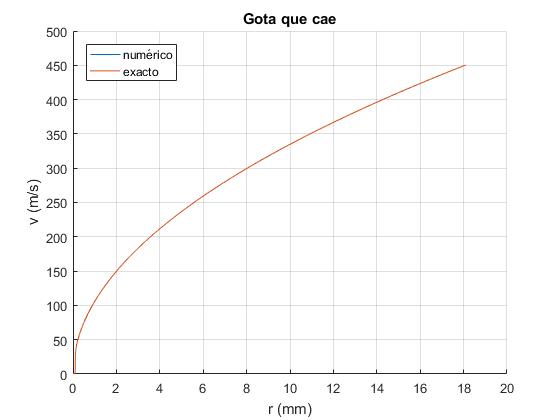
Representamos la velocidad de la gota v en función de su radio r. Vemos que la solución numérica coincide con la expresión analítica que hemos obtenido de la velocidad en función del radio v(r).

Rozamiento

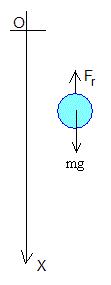
Las ecuaciones del movimiento de una gota de masa m que cae a través de la niebla son:

${\displaystyle \begin{array}{l}m\frac{dv}{dt}+v\frac{dm}{dt}=mg-\frac{1}{2}{C}_D{\rho }_{a}A{v}^2\\ \frac{dm}{dt}=k{m}^{\alpha }{v}^{\beta }\end{array}}$

Donde F_r es la fuerza de rozamiento que experimenta un cuerpo que se mueve en el seno de un fluido. Para una gota esférica de radio r

${\displaystyle \begin{array}{l}m=\rho \frac{4}{3}\pi r^3\\ \frac{dv}{dt}=g-3\frac{v}{r}\frac{dr}{dt}-\frac{3}{8}\frac{{\rho }_a}{\rho }{C}_D\frac{v^2}{r}\\ \frac{dr}{dt}=\gamma r^{3\alpha -2}{v}^{\beta }\end{array}}$

Donde C_D se denomina coeficiente de arrastre, ρ_a=0.856 kg/m³ es la densidad del fluido (aire) y ρ=1000 kg/m³ la densidad del agua

El coeficiente de arrastre es una función del número de Reynolds, Re. El número Re se define para un objeto esférico de radio r

${\displaystyle \mathrm{Re}=\frac{2rv}{\eta }}$

η=2.06·10^-5 m²/s es la viscosidad del fluido (aire).

Para resolver estas ecuaciones es necesario establecer una relación entre el coeficiente de arrastre C_D y el número de Reynolds, Re para un intervalo particular de números Re. Por ejemplo, si las gotas se mueven en el aire en régimen laminar Re<1 entonces C_D=24/Re. La fuerza de rozamiento es proporcional a la velocidad (fórmula de Stokes). Para otros intervalos se pueden encontrar expresiones que ajustan a los datos experimentales. En el libro citado en las referencias, se sugiere la fórmula

${\displaystyle C_D=\frac{12}{\sqrt{\mathrm{Re}}}}$

El sistema de dos ecuaciones diferenciales se transforma en

${\displaystyle \begin{array}{l}\frac{dv}{dt}=g-3\gamma r^{3\alpha -3}{v}^{\beta +1}-\frac{9}{2\sqrt{2}}\frac{{\rho }_a}{\rho }\sqrt{\eta }{\left(\frac{v}{r}\right)}^{3/2}\\ \frac{dr}{dt}=\gamma r^{3\alpha -2}{v}^{\beta }\end{array}}$

Consideremos el caso α=2/3, β=1

${\displaystyle \begin{array}{l}\delta =\frac{9}{2\sqrt{2}}\frac{0.856}{1000}\sqrt{2.06·{10}^{-5}}=0.0124\\ \frac{dv}{dt}=g-3\gamma \frac{v^2}{r}-\delta {\left(\frac{v}{r}\right)}^{3/2}\\ \frac{dr}{dt}=\gamma v\end{array}}$

r0=0.0001;
gamma=2.5e-7;
delta=0.0124;
%x(1) es la velocidad, x(2) es el radio de la gota
f=@(t,x) [9.81-3*gamma*x(1)^2/x(2)-delta*(x(1)/x(2))^(3/2); gamma*x(1)];
[t,x]=ode45(f,[0,150],[0,r0]);
subplot(1,2,1)
plot(t,x(:,2)*1000)
grid on
xlabel('t (s)')
ylabel('r (mm)')
subplot(1,2,2)
plot(t,x(:,1))
grid on
xlabel('t (s)')
ylabel('v(m/s)')
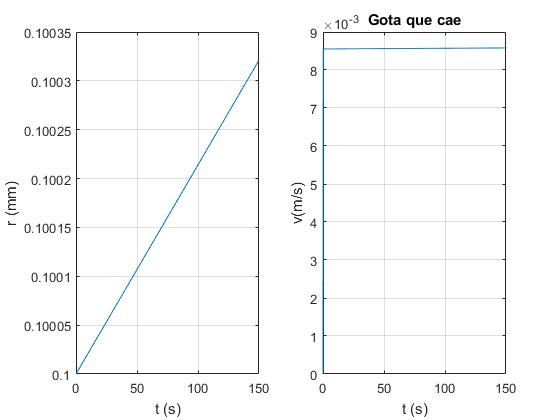
title('Gota que cae')

Vemos que la velocidad de la gota alcanza rápidamente un valor límite constante (derecha), y que el radio de la gota crece linealmente con el tiempo (izquierda)

Referencias

Adawi I. Comments on the raindrop problem. Am. J. Phys. 54 (8) August 1986, pp. 739-740

Alan D. Sokal The falling raindrop, revisited. Am. J. Phys. 78 (6) June 2010, pp. 643-644

Carl E. Mungan More about the falling raindrop. Am. J. Phys. 78 (12) December 2010. pp. 1421

Este artículo está disponible en la dirección: https://www.usna.edu/Users/physics/mungan/Publications/Publications.php#fndtn-panel120162017

Russell L. Herman. A Course in Mathematical Methods for Physicist. CRC Press (2014), 117-123