Rebotes en el plano inclinado (I)

Situación inicial: caída libre

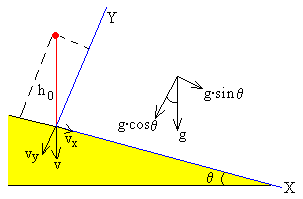
La pelota se deja caer verticalmente desde una altura h₀. Parte con velocidad inicial cero, desde la posición

x₀=-h₀·sinθ,
y₀=h₀·cosθ

Las componentes de la aceleración son

a_x=g·sinθ
a_y=-g·cosθ

El movimiento a lo largo de la recta vertical es la composición de dos movimientos uniformemente acelerados. Las componentes de la velocidad en función del tiempo son

v_x= g·sinθ·t
v_y=-g·cosθ·t

Las coordenadas de la pelota son

${\displaystyle \begin{array}{l}x=-h_0\sin \theta +\frac{1}{2}g\sin \theta ·t^2\\ y=h_0\cos \theta -\frac{1}{2}g\cos \theta ·t^2\end{array}}$

La trayectoria es la línea recta y=-x/tanθ

La pelota llega al origen x=0, y=0 en el instante

${\displaystyle t_0=\sqrt{\frac{2h_0}{g}}}$

La velocidad con la que llega al origen es

v_x= g·sinθ·t₀
v_y=-g·cosθ·t₀

Primera etapa

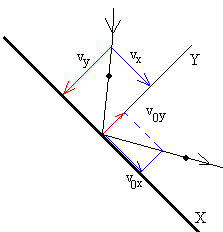
La pelota rebota:

• La componente X de su velocidad no se modifica, v_0x=v_x

• La componente Y de su velocidad cambia de sentido y disminuye su módulo, v_0y=-e·v_y

La pelota parte del origen x₀=0, y₀=0, en el instante t₀, con una velocidad inicial

v_0x= g·sinθ·t₀
v_0y=e·g·cosθ·t₀

Las componentes de la velocidad en función del tiempo son

v_x=v_0x+g·sinθ·(t-t₀)
v_y=v_0y-g·cosθ·(t-t₀)

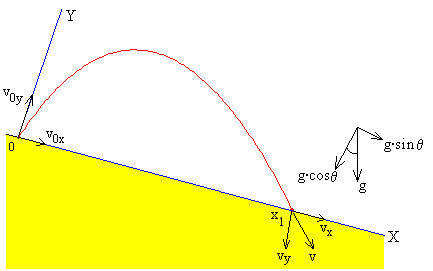
Las coordenadas de la pelota son

${\displaystyle \begin{array}{l}x=v_{0x}(t-t_0)+\frac{1}{2}g\sin \theta ·{\left(t-t_0\right)}^2\\ y=v_{0y}(t-t_0)-\frac{1}{2}g\cos \theta ·{\left(t-t_0\right)}^2\end{array}}$

La pelota llega al plano inclinado cuando y=0, en el instante t₁.

${\displaystyle t_1=t_0+\frac{2v_{0y}}{g·\cos \theta }=t_0(1+2e)}$

La posición x₁ del punto de impacto es

${\displaystyle x_1=2g{t}_0^{2}e(1+e)\sin \theta }$

Las componentes de la velocidad final son

v_x=g·t₀·(1+2e)·sinθ
v_y=-e·g·t₀·cosθ

Segunda etapa

La pelota rebota:

• La componente X de su velocidad no se modifica, v_1x=v_x

• La componente Y de su velocidad cambia de sentido y disminuye su módulo, v_1y=-e·v_y

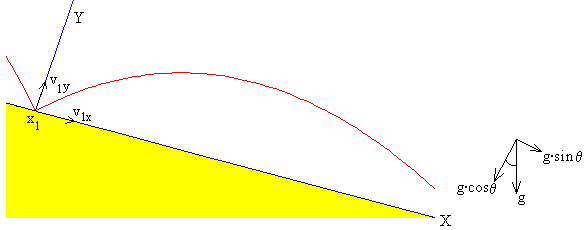
La pelota parte de la posición x₁, y₁=0 en el instante t₁, con una velocidad inicial

v_1x= g·t₀·(1+2e)·sinθ
v_1y=e²·g·t₀·cosθ

Las componentes de la velocidad en función del tiempo son

v_x=v_1x+ g·sinθ·(t-t₁)
v_y=v_1y-g·cosθ·(t-t₁)

Las coordenadas de la pelota son

${\displaystyle \begin{array}{l}x=x_1+v_{1x}(t-t_1)+\frac{1}{2}g\sin \theta ·{\left(t-t_1\right)}^2\\ y=v_{1y}(t-t_1)-\frac{1}{2}g\cos \theta ·{\left(t-t_1\right)}^2\end{array}}$

La pelota llega al plano inclinado cuando y=0, en el instante t₂.

${\displaystyle t_2=t_1+\frac{2v_{1y}}{g·\cos \theta }=t_0(1+2e+2e^2)}$

La posición x₂ del punto de impacto es

${\displaystyle x_2=2g{t}_0^2(e+2e^2+2e^3+e^4)\sin \theta }$

Las componentes de la velocidad final son

v_x=g·t₀·(1+2e+2e²)·sinθ
v_y=-e²·g·t₀·cosθ

Tercera etapa

La pelota rebota:

• La componente X de su velocidad no se modifica, v_2x=v_x

• La componente Y de su velocidad cambia de sentido y disminuye su módulo, v_2y=-e·v_y

La pelota parte de la posición  x₂, y₂=0, en el instante t₂, con una velocidad inicial

v_2x= g·t₀·(1+2e+2e²)·sinθ
v_2y=e³·g·t₀·cosθ

Las componentes de la velocidad en función del tiempo son

v_x=v_2x+ g·sinθ·(t-t₂)
v_y=v_2y-g·cosθ·(t-t₂)

Las coordenadas de la pelota son

${\displaystyle \begin{array}{l}x=x_2+v_{2x}(t-t_2)+\frac{1}{2}g\sin \theta ·{\left(t-t_2\right)}^2\\ y=v_{2y}(t-t_2)-\frac{1}{2}g\cos \theta ·{\left(t-t_2\right)}^2\end{array}}$

La pelota llega al plano inclinado cuando y=0, en el instante t₃.

${\displaystyle t_3=t_2+\frac{2v_{2y}}{g·\cos \theta }=t_0(1+2e+2e^2+2e^3)}$

La posición x₃ del punto de impacto es

${\displaystyle x_3=2g{t}_0^2(e+2e^2+3e^3+3e^4+2e^5+e^6)\sin \theta }$

Las componentes de la velocidad final son

v_x=g·t₀·(1+2e+2e²+2e³)·sinθ
v_y=-e³·g·t₀·cosθ

Cuarta etapa

La pelota rebota:

• La componente X de su velocidad no se modifica, v_3x=v_x

• La componente Y de su velocidad cambia de sentido y disminuye su módulo, v_3y=-e·v_y

La pelota parte de x₃, y₃=0, en el instante t₃, con una velocidad inicial

v_3x= g·t₀·(1+2e+2e²+2e³)·sinθ
v_3y=e⁴·g·t₀·cosθ

Las componentes de la velocidad de la pelota en función del tiempo son

v_x=v_3x+ g·sinθ·(t-t₃)
v_y=v_3y-g·cosθ·(t-t₃)

Las coordenadas de la pelota son

${\displaystyle \begin{array}{l}x=x_3+v_{3x}(t-t_3)+\frac{1}{2}g\sin \theta ·{\left(t-t_3\right)}^2\\ y=v_{3y}(t-t_3)-\frac{1}{2}g\cos \theta ·{\left(t-t_3\right)}^2\end{array}}$

La pelota llega al plano inclinado cuando y=0, en el instante t₄.

${\displaystyle t_4=t_3+\frac{2v_{3y}}{g·\cos \theta }=t_0(1+2e+2e^2+2e^3+2e^4)}$

La posición x₄ del punto de impacto es

${\displaystyle x_4=2g{t}_0^2(e+2e^2+3e^3+4e^4+4e^5+3e^6+2e^7+e^8)\sin \theta }$

Las componentes de la velocidad final son

v_x=g·t₀·(1+2e+2e²+2e³+2e⁴)·sinθ
v_y=-e⁴·g·t₀·cosθ

Ejemplo

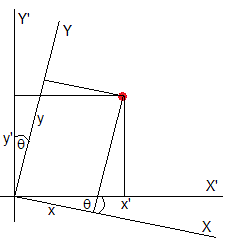
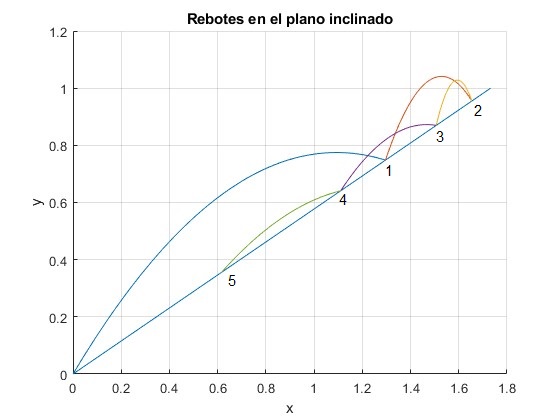
Dejamos caer una pelota desde una altura h₀=1 m, sobre un plano inclinado θ=15°. El coeficiente de restitución es e=0.8. Vamos a representar la trayectoria de la pelota sobre el plano inclinado. Para ello es necesario girar los ejes un ángulo θ tal como se aprecia en la figura

${\displaystyle \{\begin{array}{l}x\text{'}=x\cos \theta +y\sin \theta \\ y\text{'}=-x\sin \theta +y\cos \theta \end{array}}$

t0=sqrt(2*1/9.8); %cae desde una altura de 1 m
th=pi/12; % plano inclinado
ex=0.8; %coeficiente de restitución
x0=0;
vx=9.8*sin(th)*t0; %velocidad inicial
vy=-9.8*cos(th)*t0;
tt=t0; %tiempo total
hold on
line([0,10*cos(th)],[0,-10*sin(th)])
for i=1:5
    v0x=vx; %velocidad inicial
    v0y=-ex*vy;
    x=@(t) x0+v0x*t+4.9*sin(th)*t.^2; %ejes X a lo largo del plano inclinado
    y=@(t) v0y*t-4.9*cos(th)*t.^2;
    xp=@(t) x(t)*cos(th)+y(t)*sin(th);
    yp=@(t) -x(t)*sin(th)+y(t)*cos(th);
    t1=2*v0y/(9.8*cos(th));
    fplot(xp,yp,[0,t1])
    tt=tt+t1;
    disp([tt,x(t1)]) %tiempo, distancia del choque al origen
    x0=x(t1);
    vx=v0x+9.8*sin(th)*t1; %velocidad final
    vy=v0y-9.8*cos(th)*t1;
end
hold off
grid on
xlabel('x')
ylabel('y')
title('Rebotes en el plano inclinado')

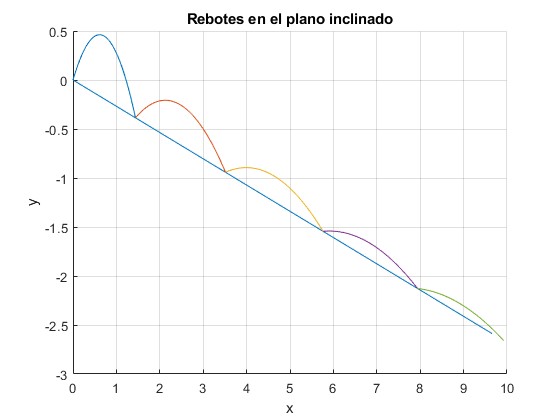
Los tiempos t₁, t₂, ... y las posiciones de impacto sobre el plano inclinado x₁, x₂, ... son

   t          x
    1.1746    1.4908
    1.7528    3.6375
    2.2154    5.9656
    2.5855    8.2188
    2.8815   10.2715

Etapa n

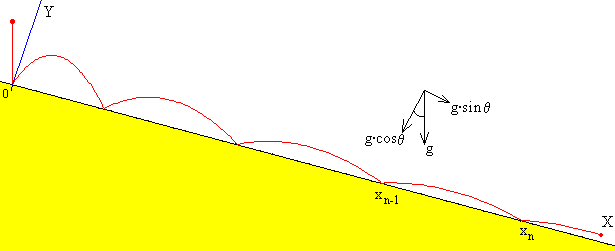
Al finalizar la etapa n, la posición de la pelota es

${\displaystyle x_n=2g{t}_0^2\left({\displaystyle \sum _{i=1}^{n}i·}\left(e^i+e^{2n+1-i}\right)\right)\sin \theta }$

que se alcanza en el instante

${\displaystyle t_n=t_0\left(1+2e\left({\displaystyle \sum _{i=0}^{n-1}{e}^i}\right)\right)}$

Las componentes de la velocidad final son

${\displaystyle \begin{array}{l}{v}_x=g·\sin \theta ·t_0\left(1+2e\left({\displaystyle \sum _{i=0}^{n-1}{e}^i}\right)\right)\\ v_y=-e^{n}g·t_0\cos \theta \end{array}}$

Después de muchos rebotes (n→∞)

Sabiendo que

${\displaystyle {\displaystyle \sum _{i=0}^{\infty }{e}^i}=\frac{1}{1-e}}$

es la suma de los infinitos términos de una progresión geométrica cuyo primer término es a₀=1, y cuya razón es e<1

${\displaystyle t_{\infty }=t_0\frac{1+e}{1-e}}$

El valor de t_∞ es idéntico al que hemos obtenido para el caso de rebotes en el plano horizontal.

Las componentes de la velocidad tienden a

${\displaystyle \begin{array}{l}{v}_x=g{t}_0\frac{1+e}{1-e}\sin \theta \\ v_y=0\end{array}}$

Teniendo en cuenta que

${\displaystyle \underset{n\to \infty }{\lim }\left({\displaystyle \sum _{i=1}^{n}i·}\left(e^i+e^{2n+1-i}\right)\right)=\frac{e}{{(1-e)}^2}}$

Comprobamos con e=0.8, y n=200

x=0.8;  %coeficiente de restitución
n=200;
k=1:n;
s=sum(k.*(x.^k+x.^(2*n+1-k)));
y=x/(1-x)^2;
disp([s, y])

>> 20.0000   20.0000

Utilizamos Math Symbolic para sumar la serie

>> syms x k n;
>> assume(x>0 & x<1);
>> sum=symsum(k*(x^k+x^(2*n+1-k)),k,1,n)
 sum =(x - x*x^n - n*x*x^n + n*x^n*x^2)/(x - 1)^2 - 
(x^n*x^2 - x^(2*n)*x^2 - n*x*x^n + n*x^n*x^2)/(x - 1)^2
>> limit(sum,n,inf)
ans =x/(x - 1)^2

La posición de los sucesivos rebotes en el plano inclinado, alcanza un límite x_∞

${\displaystyle x_{\infty }=2g{t}_0^2\frac{e}{{(1-e)}^2}\sin \theta }$

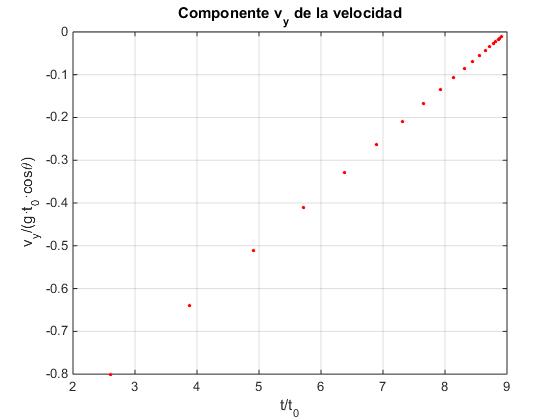
En la figura, se muestra la variación de la componente Y de la velocidad, al final de cada una de las etapas del movimiento de la pelota. Como vemos v_y tiende a cero cuando t→t_∞.

e=0.8; %coeficiente de restitución
N=20;
t=zeros(N,1);
v=zeros(N,1);
for n=1:N;
    k=1:n;
    t(n)=1+2*e*sum(e.^(k-1));
    v(n)=-e^n;
end
plot(t,v,'ro','markersize',2,'markerfacecolor','r')
grid on
xlabel('t/t_0')
ylabel('v_y/(g·t_0·cos\theta)')
title('Componente v_y de la velocidad')

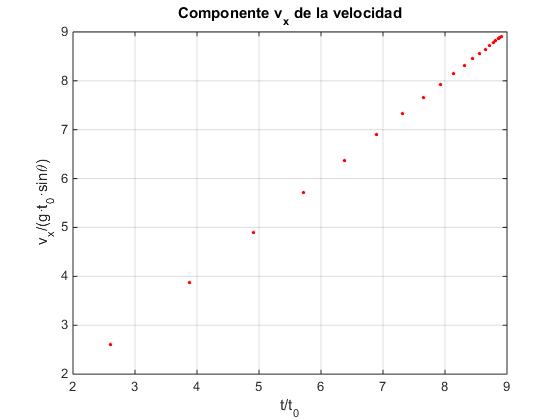
En la figura, se muestra la variación de la componente X de la velocidad, al final de cada una de las etapas del movimiento de la pelota. Como vemos v_x tiende a un valor límite cuando t→t_∞.

e=0.8; %coeficiente de restitución
N=20;
t=zeros(N,1);
v=zeros(N,1);
for n=1:N;
    k=1:n;
    t(n)=1+2*e*sum(e.^(k-1));
    v(n)=t(n);
end
plot(t,v,'ro','markersize',2,'markerfacecolor','r')
grid on
xlabel('t/t_0')
ylabel('v_x/(g·t_0·sin\theta)')
title('Componente v_x de la velocidad')

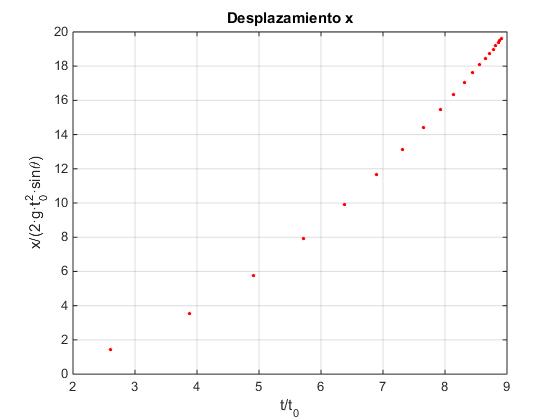
En la figura, se muestra la posición x_i de la pelota en el momento que rebota en el plano inclinado Como vemos x no crece indefinidamente, sino que tiende a un valor límite x_∞ cuando t→t_∞.

e=0.8; %coeficiente de restitución
N=20;
t=zeros(N,1);
x=zeros(N,1);
for n=1:N;
    k=1:n;
    t(n)=1+2*e*sum(e.^(k-1));
    x(n)=sum(k.*(e.^k+e.^(2*n+1-k)));
end
plot(t,x,'ro','markersize',2,'markerfacecolor','r')
grid on
xlabel('t/t_0')
ylabel('x/(2·g·t_0^2·sin\theta)')
title('Desplazamiento x')

Actividades

Se introduce

• El ángulo del plano inclinado θ, en el control titulado Pendiente
• El coeficiente de restitución e, en el control titulado Coef. restitución
• La altura desde la que se deja cera la pelota h₀, se ha fijado en h₀=1 m.

Se pulsa el botón titulado Nuevo

Se observa los sucesivos rebotes de la pelota en el plano inclinado.

En la parte superior, se proporcionan los datos de la posición y velocidad de la pelota en función del tiempo, referidos a un sistema de Referencia en el que el eje X está en el plano horizontal y el eje Y es perpendicular al mismo

Rebotes en el plano inclinado (II)

Describimos en este apartado, una variante del problema descrito en el primero. Se lanza la pelota hacia el origen con velocidad v₀ haciendo un ángulo φ con el plano inclinado.

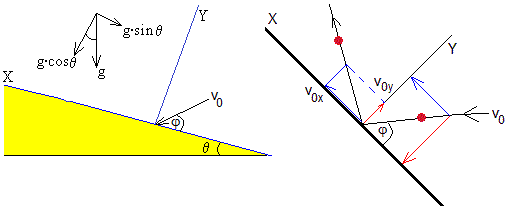
Cuando la pelota choca con el plano inclinado

• La componente X de su velocidad no se modifica, v_0x=v₀cosφ
• La componente Y de su velocidad cambia de sentido y disminuye su módulo, v_0y=e·v₀sinφ

Vamos a estudiar este ejemplo

• Angulo del plano inclinado, θ=π/6 (30°)
• Coeficiente de restituación, e=0.8
• Velocidad inicial de la pelota, v₀=5 m/s
• Angulo de la velocidad, φ=π/6, se lanza horizontalmente hacia el origen

Primera etapa

• La posición inicial para la primera etapa del movimiento es x₀=0 m, parte del origen
• La velocidad inicial es, v_0x=4.3301 m/s, v_0y=2.0000 m/s

Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}\{\begin{array}{l}{v}_x=v_{0x}-g\sin \theta ·t\\ v_y=v_{0y}-g\cos \theta ·t\end{array}\\ \{\begin{array}{l}x=v_{0x}t-\frac{1}{2}g\sin \theta ·t^2\\ y=v_{0y}t-\frac{1}{2}g\cos \theta ·t^2\end{array}\end{array}}$

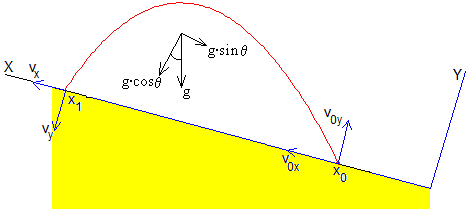
La pelota llega al plano inclinado y=0, en el instante t₁

${\displaystyle t_1=\frac{2v_{0y}}{g\cos \theta }=\frac{2e{v}_0\sin \phi }{g\cos \theta }}$

Para este ejemplo, t₁=0.4713 s, la posición del punto de impacto es

${\displaystyle x_1=v_0\cos \phi ·t_1-\frac{1}{2}g\sin \theta ·t_1^2}$

x₁=1.4966 m. Las componentes de la velocidad final antes del próximo choque son

${\displaystyle \{\begin{array}{l}{v}_x=v_0\cos \phi -g\sin \theta ·t_1\\ v_y=e{v}_0\cos \phi -g\cos \theta ·t_1\end{array}}$

v_x=2.0207 m/s, v_y=-2.0000 m/s.

La componente v_x de la velocidad se anula en el instante

${\displaystyle t_x=\frac{v_0\cos \phi }{g\sin \theta }}$

t_x=0.8837 s. A partir de este instante, la pelota inicia su movimiento hacia abajo, pero antes, rebotará sobre el plano inclinado como vamos a comprobar

Segunda etapa

• La posición inicial para la segunda etapa del movimiento es x₁=1.4966 m,
• La velocidad inicial es, v_0x=v_x=2.0207 m/s, v_0y=-e·v_y=1.6000 m/s

Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}\{\begin{array}{l}{v}_x=v_{0x}-g\sin \theta ·\left(t-t_1\right)\\ v_y=v_{0y}-g\cos \theta ·\left(t-t_1\right)\end{array}\\ \{\begin{array}{l}x=x_1+v_{0x}\left(t-t_1\right)-\frac{1}{2}g\sin \theta ·{\left(t-t_1\right)}^2\\ y=v_{0y}\left(t-t_1\right)-\frac{1}{2}g\cos \theta ·{\left(t-t_1\right)}^2\end{array}\end{array}}$

La pelota llega al plano inclinado y=0, en el instante t₂

${\displaystyle t_2=t_1+\frac{2v_{0y}}{g\cos \theta }}$

Para este ejemplo, t₂=0.8484 s, la posición del punto de impacto es

${\displaystyle x_2=x_1+v_{0x}\left(t_2-t_1\right)-\frac{1}{2}g\sin \theta ·{\left(t_2-t_1\right)}^2}$

x₂=1.9102 m. Las componentes de la velocidad final antes del próximo choque son

${\displaystyle \{\begin{array}{l}{v}_x=v_{0x}-g\sin \theta ·\left(t_2-t_1\right)\\ v_y=v_{0y}-g\cos \theta ·\left(t_2-t_1\right)\end{array}}$

v_x=0.1732 m/s, v_y=-1.6000 m/s.

Tercera etapa

• La posición inicial para la tercera etapa del movimiento es x₂=1.9102 m,
• La velocidad inicial es, v_0x=v_x=0.1732 m/s, v_0y=-e·v_y=1.2800 m/s

Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}\{\begin{array}{l}{v}_x=v_{0x}-g\sin \theta ·\left(t-t_2\right)\\ v_y=v_{0y}-g\cos \theta ·\left(t-t_2\right)\end{array}\\ \{\begin{array}{l}x=x_2+v_{0x}\left(t-t_2\right)-\frac{1}{2}g\sin \theta ·{\left(t-t_2\right)}^2\\ y=v_{0y}\left(t-t_2\right)-\frac{1}{2}g\cos \theta ·{\left(t-t_2\right)}^2\end{array}\end{array}}$

La pelota llega al plano inclinado y=0, en el instante t₃

${\displaystyle t_3=t_2+\frac{2v_{0y}}{g\cos \theta }}$

Para este ejemplo, t₃=1.1500 s. Este tiempo es mayor que t_x, la componente v_x de la velocidad ha cambiado de signo y la partícula cambia el sentido del movimiento (hacia abajo)

La posición del punto de impacto es

${\displaystyle x_3=x_2+v_{0x}\left(t_3-t_2\right)-\frac{1}{2}g\sin \theta ·{\left(t_3-t_2\right)}^2}$

x₃=1.7396 m que es menor que x₂. Las componentes de la velocidad final antes del próximo choque son

${\displaystyle \{\begin{array}{l}{v}_x=v_{0x}-g\sin \theta ·\left(t_3-t_2\right)\\ v_y=v_{0y}-g\cos \theta ·\left(t_3-t_2\right)\end{array}}$

v_x=-1.3048 m/s (ha cambiado de signo), v_y=-1.2800 m/s.

Etapa n

Representamos la trayectoria de la pelota

th=pi/6; % plano inclinado 30º
ex=0.8; %coeficiente de restitución
x0=0; %parte del origen
v0=5; %velocidad inicial
phi=th; %ángulo de la velocidad con el plano inclinado
vx=v0*cos(phi); %velocidad inicial
vy=-v0*sin(phi);
tt=0; %tiempo total
hold on
line([0,2*cos(th)],[0,2*sin(th)])
disp(['   t','          x']) 
for i=1:5
    v0x=vx; %velocidad inicial
    v0y=-ex*vy;
    x=@(t) x0+v0x*t-4.9*sin(th)*t.^2; %ejes X a lo largo del plano inclinado
    y=@(t) v0y*t-4.9*cos(th)*t.^2;
    xp=@(t) x(t)*cos(th)-y(t)*sin(th);
    yp=@(t) x(t)*sin(th)+y(t)*cos(th);
    t1=2*v0y/(9.8*cos(th));
    fplot(xp,yp,[0,t1])
    tt=tt+t1;
    disp([tt,x(t1)]) %tiempo, distancia del impacto al origen
    x0=x(t1);
    vx=v0x-9.8*sin(th)*t1; %velocidad final
    vy=v0y-9.8*cos(th)*t1;
end
hold off
grid on
xlabel('x')
ylabel('y')
title('Rebotes en el plano inclinado')

Los tiempos t₁, t₂, ... y las posiciones de impacto sobre el plano inclinado x₁, x₂, ... son

   t          x
    0.4713    1.4966
    0.8484    1.9102
    1.1500    1.7395
    1.3913    1.2820
    1.5843    0.7106

Actividades

Se introduce

• El ángulo del plano inclinado θ, en el control titulado Pendiente
• El coeficiente de restitución e, en el control titulado Coef. restitución
• La velocidad inicial v₀ con la que se lanza la pelota, en el control titulado Velocidad inicial
• En la dirección φ, ángulo que forma con el plano inclinado, en el control titulado Angulo

Se pulsa el botón titulado Nuevo

Se observa los sucesivos rebotes de la pelota en el plano inclinado.

En la parte superior, se proporcionan los datos de la posición y velocidad de la pelota en función del tiempo

Referencias

Physics challenges for teachers and students. Solutions to October 2004. The Physics Teacher, 42 (2004) pp. S2