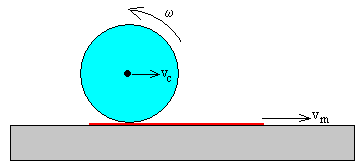
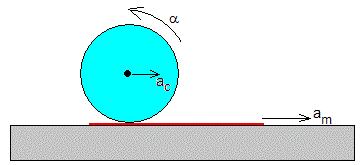
En la figura, se representa un cuerpo redondo de masa m y radio R que rueda sin deslizar sobre un mantel que se desplaza hacia la derecha con velocidad constante v_m. Vamos a calcular la velocidad del centro de masa de dicho cuerpo v_c respecto de la mesa y su velocidad angular ω de rotación.

Dinámica

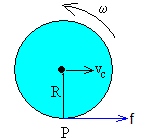
La fuerza f que ejerce el mantel sobre el cuerpo redondo actúa en el punto de contacto P. Las otras dos fuerzas: el peso y la reacción del plano horizontal no contribuyen al movimiento.

Las ecuaciones del movimiento son:

• Movimiento de traslación del centro de masas. a_c es la aceleración del cuerpo relativa a la mesa

f=m·a_c

• Movimiento de rotación alrededor de un eje que pasa por el c.m.

f·R=I_c·α

donde I_c=kmR², siendo k=1 para un aro, k=1/2 para un cilindro y k=2/5 para una esfera.

Las dos ecuaciones nos permiten relacionar ambas aceleraciones a_c=k·Rα

La misma relación se establece entre las velocidades v_c de traslación del c.m. y la velocidad angular de rotación alrededor de un eje que pase por el c.m.

v_c=k·Rω

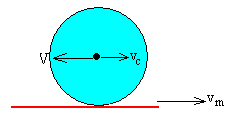
Si el cuerpo rueda sin deslizar sobre el mantel, la velocidad V del c.m. respecto del mantel será V=ωR y estará dirigida hacia la izquierda ya que la velocidad angular de rotación ω es de sentido contrario a las agujas del reloj. Teniendo en cuenta el signo, la relación entre ambas velocidades será v_c =-kV

Si la velocidad del mantel es v_m se cumplirá que V=v_c-v_m

Conocida la velocidad v_m del mantel calculamos la velocidad v_c del c.m. del cuerpo respecto de la mesa

${\displaystyle v_c=\frac{k·v_m}{1+k}}$

y la velocidad relativa V del cuerpo respecto del mantel

${\displaystyle V=-\frac{v_m}{1+k}}$

Si d es la distancia inicial que hay entre el punto P de contacto entre el cuerpo y el mantel y su borde izquierdo. El tiempo que emplea el cilindro en abandonarlo es t=d/|V|. En ese mismo tiempo, el c.m. del cilindro ha recorrido hacia la derecha una distancia x=v_c·t=k·d.

Momento angular

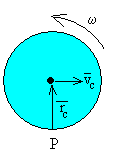
La fuerza exterior F que hace moverse al cilindro está aplicada en el punto P. El momento de dicha fuerza es cero. Por lo que el momento angular respecto de P debe de ser constante.

Para un sistema de partículas la relación entre el momento angular respecto a un eje que pasa por el c.m. y el momento angular respecto de un eje instantáneo que pasa por P es

${\displaystyle \overrightarrow{L}=\overrightarrow{L_{cm}}+m\overrightarrow{r_{cm}}\times \overrightarrow{v_{cm}}}$

Los dos momentos angulares tienen la misma dirección (perpendicular al plano del dibujo) y sentidos opuestos

L=I_cω-mRv_c=0

Escribiendo I_c=kmR², obtenemos de nuevo, la misma relación entre la velocidad de traslación del c.m. y la velocidad de rotación ω.

v_c=kRω

Cuando el cuerpo redondo abandona el mantel, no puede moverse ni a la izquierda ni a la derecha, queda completamente en reposo, ya que de otro modo el momento angular dejaría de ser nulo.

Actividades

Se introduce

• La velocidad v_m del mantel en el control titulado Velocidad
• Se elige el tipo de cuerpo que rueda, un cilindro, aro o esfera activando el botón de radio correspondiente.
• El radio R y la masa m del cuerpo redondo se han fijado en una unidad.

Se pulsa el botón titulado Nuevo

Se observa el movimiento de traslación del c.m. del cuerpo respecto de la mesa hacia la derecha mientras rueda hacia la izquierda sobre el mantel.

Relacionamos el desplazamiento x del del c.m. respecto de la mesa con el desplazamiento del cuerpo sobre el mantel d para cada uno de los cuerpos.

Observamos que cuando abandona el mantel, el cuerpo permanece en reposo.

La aceleración del mantel es a_m

Estudiamos el caso en el que la aceleración del mantel es constante e igual a a_m

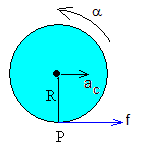
Las ecuaciones del movimiento son:

• Movimiento de traslación del centro de masas. a_c es la aceleración del cuerpo relativa a la mesa

f=m·a_c

• Movimiento de rotación alrededor de un eje que pasa por el c.m.

f·R=I_c·α

donde I_c=kmR², siendo k=1 para un aro, k=1/2 para un cilindro y k=2/5 para una esfera.

Las dos ecuaciones nos permiten relacionar ambas aceleraciones a_c=k·Rα

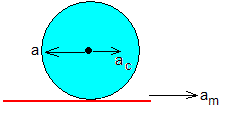
Si el cuerpo rueda sin deslizar sobre el mantel, la aceleración a del c.m. respecto del mantel será a=αR y estará dirigida hacia la izquierda ya que la aceleración angular de rotación α es de sentido contrario a las agujas del reloj. Teniendo en cuenta el signo, la relación entre ambas aceleraciones será a_c =-ka

Si la aceleración del mantel es a_m se cumplirá que a=a_c-a_m

Conocida la aceleración a_m del mantel, calculamos la aceleración a_c del c.m. del cuerpo respecto de la mesa

${\displaystyle a_c=\frac{k·a_m}{1+k}}$

y la aceleración relativa a del cuerpo respecto del mantel

${\displaystyle a=-\frac{a_m}{1+k}}$

La fuerza f que ejerce el mantel sobre el cuerpo es

${\displaystyle f=m{a}_c=m\frac{k}{1+k}{a}_m}$

Esta fuerza tiene que ser menor que la máxima, μ_sN=μ_smg

La aceleración a_m del mantel tiene que ser menor que la máxima posible

${\displaystyle \begin{array}{l}f\le {\mu }_{s}mg\\ a_m\le {\mu }_{s}g\frac{k+1}{k}\end{array}}$

Relacionamos las aceleraciones, velocidades y desplazamientos del centro de masa del cuerpo y del mantel

${\displaystyle \begin{array}{l}{a}_c=\frac{k}{k+1}{a}_m\\ v_c=\frac{k}{k+1}{v}_m\\ \Delta x_c=\frac{k}{k+1}\Delta x_m\end{array}}$

Supondremos que el cuerpo y el mantel parten del reposo en el instante t=0

Por ejemplo, para un cuerpo cilíndrico k=1/2, los desplazamientos, en el intervalo de tiempo Δt, del cuerpo y del mantel están relacionados por Δx_c=Δx_m/3

Problema

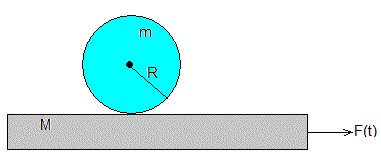
Un cilindro de masa m y momento de inercia mR²/2 se coloca sobre una plataforma de masa M. Sobre la plataforma actúa una fuerza periódica F(t)=F₀cos(ω₀t).

La plataforma desliza sin rozamiento sobre el plano horizontal. El cilindro rueda sobre una superficie horizontal rugosa cuyo coeficiente cinético es μ_k.

Vamos a calcular las velocidades máximas de la plataforma v_y, y del cilindro v_x respecto del laboratorio

Supondremos que el coeficiente estático μ_s es suficientemente grande para que se cumpla a_m≤ 3μ_sg, para k=1/2, es decir, un cilindro, a_m es la aceleración de la plataforma

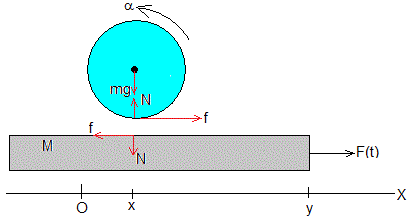
• Las ecuaciones del movimiento (traslación y rotación) del cilindro son

Sea x la posición del centro del cilindro

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=f\\ I\frac{d^2\theta }{d{t}^2}=fR,mR\frac{d^2\theta }{d{t}^2}=2f\end{array}}$

• La ecuación del movimiento de la plataforma es

Sea y la posición dela plataforma

${\displaystyle M\frac{d^{2}y}{d{t}^2}=F-f}$

El cilindro rueda sin deslizar, si

${\displaystyle y-x=R\theta }$

y-x es el desplazamiento del cilindro relativo a la plataforma y θ es el ángulo girado por el cilindro

${\displaystyle \begin{array}{l}\frac{d^{2}y}{d{t}^2}-\frac{d^{2}x}{d{t}^2}=R\frac{d^2\theta }{d{t}^2}\\ \frac{F-f}{M}-\frac{f}{m}=\frac{2f}{m}\\ \frac{F}{M}=f\left(\frac{1}{M}+\frac{3}{m}\right)\\ f=\frac{F}{1+3\frac{M}{m}}\end{array}}$

• La velocidad de la plataforma es

${\displaystyle \begin{array}{l}M\frac{d{v}_y}{dt}=F-f\\ \frac{d{v}_y}{dt}=\frac{3}{m+3M}F\\ \frac{d{v}_y}{dt}=\frac{3}{m+3M}{F}_0\cos \left({\omega }_{0}t\right)\\ {\displaystyle \underset{0}{\overset{v_y}{\int }}d{v}_y=}\frac{3F_0}{m+3M}{\displaystyle \underset{0}{\overset{t}{\int }}\cos \left({\omega }_{0}t\right)·dt}\\ v_y=\frac{3F_0}{m+3M}\frac{1}{{\omega }_0}\sin \left({\omega }_{0}t\right)\end{array}}$

• La velocidad del centro de masas del cilindro es

${\displaystyle \begin{array}{l}m\frac{d{v}_x}{dt}=f\\ \frac{d{v}_x}{dt}=\frac{1}{m+3M}{F}_0\cos \left({\omega }_{0}t\right)\\ v_x=\frac{F_0}{m+3M}\frac{1}{{\omega }_0}\sin \left({\omega }_{0}t\right)\end{array}}$

• La velocidad angular de rotación del cilindro es

${\displaystyle \begin{array}{l}\frac{d\omega }{dt}=\frac{1}{R}\frac{2}{m+3M}{F}_0\cos \left({\omega }_{0}t\right)\\ \omega =\frac{1}{{\omega }_{0}R}\frac{2F_0}{m+3M}\sin \left({\omega }_{0}t\right)\end{array}}$

Se cumple que v_y-v_x=Rω. El cilindro rueda sin deslizar sobre la plataforma

• La posición y de la plataforma en función del tiempo t

${\displaystyle \begin{array}{l}y=\frac{3F_0}{m+3M}\frac{1}{{\omega }_0}{\displaystyle \underset{0}{\overset{t}{\int }}\sin \left({\omega }_{0}t\right)·dt}\\ y=\frac{3F_0}{m+3M}\frac{1}{{\omega }_0^2}\left(1-\cos \left({\omega }_{0}t\right)\right)\end{array}}$

• La posición x del centro del cilindro en función del tiempo t

${\displaystyle x=\frac{F_0}{m+3M}\frac{1}{{\omega }_0^2}\left(1-\cos \left({\omega }_{0}t\right)\right)}$

La velocidad alcanza su valor máximo en el instante ω₀t₁=π/2

Movimiento del cilindro sobre la plataforma en reposo

Una situación interesante se produce cuando la plataforma se detiene bruscamente en este instante t₁. Supondremos que las velocidades de traslación y angular de rotación del cilindro no se ven afectadas

La velocidad de traslación del centro del cilindro en el instante t₁ sería

${\displaystyle v_1=\frac{F_0}{m+3M}\frac{1}{{\omega }_0}}$

La velocidad angular de rotación del cilindro en dicho instante sería

${\displaystyle {\omega }_{1}R=\frac{2F_0}{m+3M}\frac{1}{{\omega }_0}}$

En la posición

${\displaystyle x_1=\frac{F_0}{m+3M}\frac{1}{{\omega }_0^2}}$

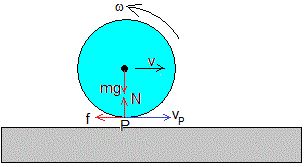
En dicho instante, no se cumple la condición de rodar sin deslizar: ω₁R es el doble de v₁

La fuerza de rozamiento f=μ_kN=μ_kmg se opone a la velocidad del punto P de contacto del cilindro con la plataforma en reposo. Como f es una fuerza constante, la aceleración es constante y también la angular

La fuerza de rozamiento f hace que el cilindro disminuya su velocidad de traslación, la angular de rotación hasta que se detiene

• Movimiento de traslación del cilindro

${\displaystyle \begin{array}{l}a=\frac{f}{m}=\frac{-{\mu }_{k}mg}{m}\\ v=v_1-{\mu }_{k}gt\end{array}}$

La velocidad v se anula en el instante t₂, cuando la posición del centro del cilindro es x₂

${\displaystyle \begin{array}{l}{t}_2=t_1+\frac{v_1}{{\mu }_{k}g}=t_1+\frac{1}{{\mu }_{k}g{\omega }_0}\frac{F_0}{m+3M}\\ x_2=x_1+v_1\left(t_2-t_1\right)-\frac{1}{2}{\mu }_{k}g{\left(t_2-t_1\right)}^2=x_1+\frac{1}{2}\frac{v_1^2}{{\mu }_{k}g}\end{array}}$

• Movimiento de rotación del cilindro

${\displaystyle \begin{array}{l}I\alpha =-fR=-{\mu }_{k}mgR\\ \alpha =\frac{-{\mu }_{k}mgR}{\frac{1}{2}m{R}^2}=-2\frac{{\mu }_{k}g}{R}\\ \omega ={\omega }_1-2\frac{{\mu }_{k}g}{R}t\end{array}}$

La velocidad angular ω se anula en el instante t₃

${\displaystyle t_3=t_1+\frac{{\omega }_{1}R}{2{\mu }_{k}g}=t_1+\frac{1}{{\mu }_{k}g{\omega }_0}\frac{F_0}{m+3M}}$

Como vemos t₃ coincide con t₂ el instante en el que el cilindro se encuentra en reposo

Representamos la velocidad v_x de traslación del cilindro y la velocidad angular de rotación ωR, en función del tiempo, para los siguientes datos

• Masa del cilindro, m= 1 kg
• Radio del cilindro, R= 1 m
• Masa de la plataforma, M= 3 kg
• Amplitud de la fuerza, F₀=5 N
• Frecuencia angular de la fuerza oscilante, ω₀=1 rad/s
• El mantel es una superficie rugosa cuyo coeficiente cinético, μ_k=0.1

m=1; %masa cilindro
M=3; %masa plataforma
R=1; %radio cilindro
F0=5; %amplitud fuerza
w0=1; %frecuencia angular
mu=0.1; %coef. cinético rozamiento
C=F0/(w0*(m+3*M));
%vy=@(t) 3*C*sin(w0*t); %velocidad mantel
vx=@(t) C*sin(w0*t); %velocidad centro cilindro
w=@(t) 2*C*sin(w0*t); %velocidad angular cilindro
t0=pi/(2*w0); %tiempo final
hold on
fplot(vx,[0,t0])
fplot(w,[0,t0])
%segunda etapa, mantel fijo
v=@(t) C-mu*9.8*(t-t0);
w=@(t) 2*C-2*mu*9.8*(t-t0);
t1=t0+C/(mu*9.8);
fplot(v,[t0,t1])
fplot(w,[t0,t1])
line([t0,t0],[0,C],'lineStyle','--')
hold off
grid on
lxlabel('t (s)')
ylabel('v,\omega·R')
title('Velocidades')

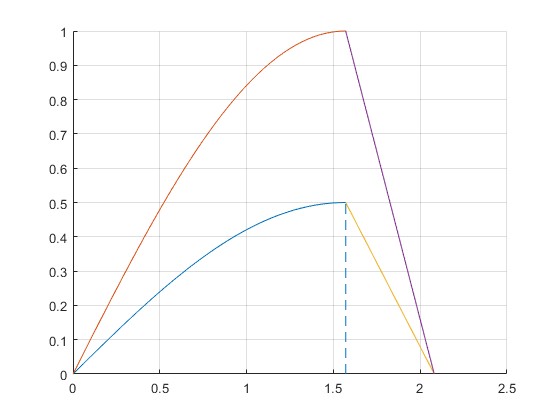
La línea a trazos marca el instante t₀

Representamos la posición x del centro del cilindro, en función del tiempo, para los mismos datos

m=1; %masa cilindro
M=3; %masa plataforma
R=1; %radio cilindro
F0=5; %amplitud fuerza
w0=1; %frecuencia angular
mu=0.1; %coef. cinético rozamiento
C=F0/(w0*(m+3*M));
x=@(t) C*(1-cos(w0*t))/w0; %posición cilindro
t0=pi/(2*w0); %tiempo final
hold on
fplot(x,[0,t0])
%segunda etapa, mantel fijo
x=@(t) C/w0+C*(t-t0)-mu*9.8*(t-t0).^2/2;
t1=t0+C/(mu*9.8);
fplot(x,[t0,t1])
line([t0,t0],[0,C/w0],'lineStyle','--')
hold off
grid on
xlabel('t (s)')
ylabel('x (m)')
title('Posición')

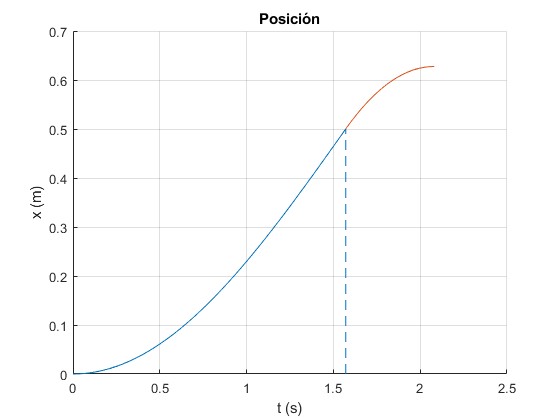
Actividades

Se introduce

• La masa de la plataforma, en el control titulado Masa M
• El coeficiente cinético, en el control titulado Coef. cinético μ_k
• La masa del cilindro se ha fijado en m=1 kg
• El radio del cilindro se ha fijado en R=1 m
• La amplitud de la fuerza se ha fijado en F₀=5N
• La frecuencia angular de la fuerza oscilante se ha fijado en, ω₀=1 rad/s

Se pulsa el botón titulado Nuevo

Observamos la plataforma en movimiento y el cilindro rodando sin deslizar sobre la plataforma

En el instante t=π/(2ω₀), la plataforma se detiene bruscamente y el cilindro rueda y desliza sobre la plataforma hasta que se detiene

En la parte superior se proporciona, el tiempo t en s y la posición x en m del centro del cilindro

Referencias

Ferguson J. Pulling the rug from under round objects. The Physics Teacher vol 39, April 2001, pp. 224-225.

R. De Luca. Physics at the grocery store. Revista Brasileira de Ensino de Física, vol. 44, e20220086 (2022)

Pan Pearl River Delta Physics Olympiad 2015. Q2