Ecuación de la catenaria

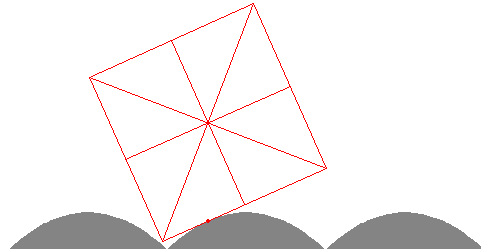
Supongamos una rueda cuadrada de lado 2a, cuyo centro de masa se mueve a lo largo de una trayectoria horizontal y permanece justo encima del punto de contacto entre uno de los lados de la rueda y el camino.

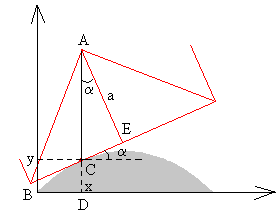
El triángulo isósceles ABE representa un octante del cuadrado. Como vemos en la figura AE=a, y AB=$\sqrt{2}a$ .

Inicialmente la esquina B del rectángulo está situada en el origen, al moverse rodando sin deslizar la longitud BC será igual a la longitud del arco OC. Por otra parte, el punto C será tal que la longitud AC+CD=AB se mantendrá constante durante todo el movimiento, es decir, el centro del rectángulo describe una trayectoria que es una recta horizontal.

Si la ordenada del punto C es y y el ángulo que forma el lado BE con la horizontal es α, la relación  AC+CD=AB se escribe

${\displaystyle \frac{a}{\cos \alpha }+y=\sqrt{2}a}$

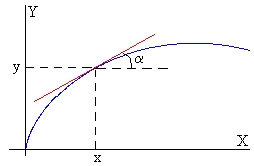
Recordando la interpretación geométrica de la derivada, la tangente del ángulo α es

${\displaystyle \tan \alpha =\frac{dy}{dx}}$

Aplicamos la conocida relación 1+tan²α=sec²α, obtenemos

${\displaystyle 1+{\left(\frac{dy}{dx}\right)}^2={\left(\frac{\sqrt{2}a-y}{a}\right)}^2}$

Hacemos la sustitución

${\displaystyle u=\frac{1}{\cos \alpha }=\sqrt{2}-\frac{y}{a}du=-\frac{1}{a}dy}$

La ecuación diferencial está lista para ser integrada

${\displaystyle -\frac{1}{a}dx=\frac{du}{\sqrt{u^2-1}}}$

La condición inicial es que la curva ha de pasar por el origen x=0, y=0 con lo que se determina la constante de integración k.

${\displaystyle {\cosh }^{-1}u=-\frac{x}{a}+kk={\cosh }^{-1}\sqrt{2}=0.88137}$

o bien,

${\displaystyle u=\cosh \left(k-\frac{x}{a}\right)}$

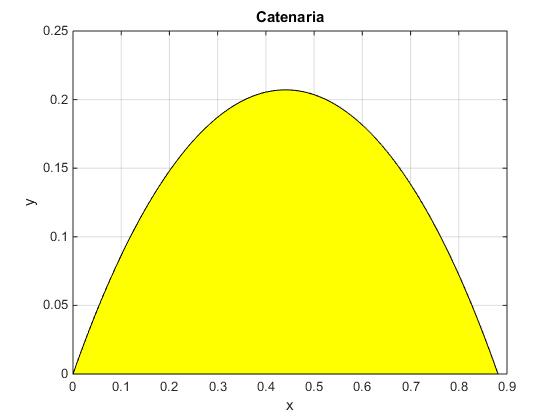
Deshaciendo el cambio, se llega a la ecuación de una catenaria

${\displaystyle y=a\left(\sqrt{2}-\cosh \left(k-\frac{x}{a}\right)\right)}$

A medida que el cuadrado rueda sin deslizar gira 90º y retorna a la configuración inicial, excepto una traslación d. Esta traslación se determina haciendo y=0 en la ecuación de la catenaria y se obtiene d=2ka.

El vértice de la catenaria se encuentra en el punto simétrico x=ka y vale $y=(\sqrt{2}-1)a$

a=0.5;
k=acosh(sqrt(2));
x=linspace(0,2*k*a,100);
y=a*(sqrt(2)-cosh(k-x/a));
fill(x,y, 'y');
xlabel('x');
ylabel('y');
title('Catenaria')

Relación entre la velocidad del c.m. y la velocidad angular de rotación

Como la distancia entre el punto de contacto C y el centro de la rueda A no es constante la conocida relación v=ω·r deja de ser válida. Para obtener la nueva relación entre v y ω procedemos del siguiente modo:

${\displaystyle v=\frac{dx}{dt}\omega =-\frac{d\alpha }{dt}}$

Si tomamos como sentido positivo de ω el de las agujas del reloj, nos fijaremos que α disminuye a medida que la rueda se mueve:

• En el comienzo de la catenaria x=0 donde α=+π/4

• En el medio x=ka (en el vértice) donde α=0

• En el extremo de la catenaria x=2ka donde α=-π/4

${\displaystyle \omega =-\frac{d\alpha }{dx}\frac{dx}{dt}=-\frac{d\alpha }{dx}v}$

Teniendo en cuenta que la pendiente de la recta tangente a la catenaria en el punto x es

${\displaystyle \frac{dy}{dx}=\tan \alpha }$

Derivamos y respecto de x en la ecuación de la catenaria

${\displaystyle \frac{dy}{dx}=\sinh \left(k-\frac{x}{a}\right)}$

Derivamos tanα con respecto de x

${\displaystyle \frac{1}{{\cos }^2\alpha }\frac{d\alpha }{dx}=-\frac{1}{a}\cosh \left(k-\frac{x}{a}\right)}$

Teniendo en cuenta que

${\displaystyle u=\frac{1}{\cos \alpha }=\cosh \left(k-\frac{x}{a}\right)}$

Nos queda

${\displaystyle \frac{d\alpha }{dx}=-\frac{1}{a}\cos \alpha \frac{d\alpha }{dt}\frac{dt}{dx}=-\frac{1}{a}\cos \alpha }$

Finalmente

ωa=v·cosα

Energía cinética de rotación y de traslación

La rueda tiene dos clases de energía cinética

• la de traslación del c.m.
• de la rotación alrededor de un eje que pasa por el c.m.

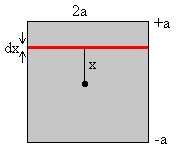
En primer lugar, calculamos el momento de inercia de una rueda cuadrada de masa M y de lado 2a respecto de un eje perpendicular al plano de la rueda y que pasa por su centro.

El momento de inercia de una varilla de masa dm y longitud 2a respecto de un eje perpendicular a la varilla delgada que pasa por su centro vale (línea de color rojo en la figura)

${\displaystyle dI=\frac{1}{12}{(2a)}^{2}dm=\frac{1}{3}{a}^{2}dm}$

Aplicando el teorema de Steiner calculamos el momento de inercia de dicha varilla respecto de un eje paralelo que pasa por el centro del cuadrado, siendo x la distancia entre ejes.

${\displaystyle d{I}_c=\frac{1}{3}{a}^{2}dm+x^{2}dm}$

La masa dm de la varilla de longitud 2a y anchura dx es

${\displaystyle dm=\frac{M}{4a^2}2adx=\frac{M}{2a}dx}$

Integrando respecto de x entre –a y +a obtenemos el momento de inercia del cuadrado respecto de un eje perpendicular al mismo y que pasa por su centro.

${\displaystyle I_c={\displaystyle \underset{-a}{\overset{a}{\int }}\left(\frac{Ma}{6}+\frac{M}{2a}{x}^2\right)}dx=\frac{2}{3}M{a}^2}$

La energía cinética de la rueda cuadrada es

${\displaystyle E_k=\frac{1}{2}M{v}^2+\frac{1}{2}\frac{2}{3}M{a}^2{\omega }^2=\frac{1}{2}M{v}^2\left(1+\frac{2}{3}{\cos }^2\alpha \right)}$

Si no hay pérdidas de energía debido al rozamiento, a medida que el cuadrado rueda sin deslizar, la energía cinética E_k se mantendrá constante. Sin embargo, la velocidad del c.m. v no es constante.

Para una esfera el cociente entre la energía cinética de rotación y de traslación del c.m. es constante, ya que la relación entre la velocidad v de traslación y la velocidad angular ω de rotación es constante,  v= ω·R

${\displaystyle \frac{E_k\text{(rotación)}}{E_k\text{ (traslación)}}=\frac{\frac{1}{2}\left(\frac{2}{5}m{R}^2\right){\omega }^2}{\frac{1}{2}m{v}^2}=\frac{2}{5}}$

Para una rueda cuadrada este cociente no es constante

${\displaystyle \frac{E_k\text{(rotación)}}{E_k\text{ (traslación)}}=\frac{\frac{1}{2}\left(\frac{2}{3}M{a}^2\right)\frac{v^2}{a^2}{\cos }^2\alpha }{\frac{1}{2}M{v}^2}=\frac{2}{3}{\cos }^2\alpha }$

Como α varía entre –π/4 y +π/4. El cociente varía entre 1/3 para α =π/4 ó α =-π/4 y 2/3 para α=0.

• En el punto medio o vértice α=0 de la catenaria la energía de rotación es máxima y la de traslación es mínima

• En los extremos α =π/4 ó α =-π/4 la energía de rotación es mínima y la de traslación es máxima.

Si tomamos la energía cinética total E_k como la unidad,

• En un extremo, la energía cinética de rotación es 1/4 de energía cinética total y la de traslación las 3/4 partes

• En el vértice de la catenaria, la energía cinética de traslación es las 3/5 partes de la energía total.

La energía cinética de traslación varía entre un mínimo de 3/5 y un máximo de 3/4 de la energía cinética total.

Ecuación del movimiento

Conocida la energía cinética total E_k, despejamos la velocidad v del centro del cuadrado

${\displaystyle v=\sqrt{\frac{2E_k/M}{1+\frac{2}{3}{\cos }^2\alpha }}}$

De la relación entre la velocidad v del centro del cuadrado y la velocidad angular ω=-dα/dt de rotación ωa=v·cosα, obtenemos la ecuación diferencial

${\displaystyle \frac{d\alpha }{dt}=-\frac{1}{a}\sqrt{\frac{2E_k}{M}}\frac{1}{\sqrt{1+\frac{2}{3}{\cos }^2\alpha }}\cos \alpha }$

que se resuelve por procedimientos numéricos con la condición inicial t=0, parte del origen x=0, α=π/4.

Una vez calculada el ángulo α de la tangente a la catenaria (véase la segunda figura de esta página) en función del tiempo t se calcula la ordenada y mediante la relación deducida al principio de esta página

${\displaystyle \frac{a}{\cos \alpha }+y=\sqrt{2}a}$

Que junto con la ecuación de la catenaria

${\displaystyle y=a\left(\sqrt{2}-\cosh \left(k-\frac{x}{a}\right)\right)}$

dan lugar a la ecuación trascendente.

${\displaystyle \frac{\text{1}}{\text{cos}\alpha }-\cosh \left(k-\frac{x}{a}\right)=0}$

que se resuelve por procedimientos numéricos para calcular el valor de la abscisa x.

Actividades

• La longitud de la mitad del lado del cuadrado se ha fijado en a=1
• La energía cinética total E_k constante de la rueda cuadrada se ha fijado de modo que

${\displaystyle \frac{1}{a}\sqrt{\frac{2E_k}{M}}=1}$

Se pulsa el botón titulado Nuevo

Se observa el movimiento de rodar sin deslizar de un cuadrado sobre un camino formado por tres catenarias invertidas. Se señala el punto de contacto entre un lado del cuadrado y la catenaria a medida que se desplaza la rueda.

Se observa que el punto de contacto está siempre debajo del centro del cuadrado y que el centro del cuadrado está siempre a la misma altura.

Observamos como cambia la velocidad v del c.m. y la velocidad de rotación ω a medida que se desplaza rueda. Un diagrama en forma de tarta nos muestra cómo cambia la energía cinética de rotación y de traslación manteniéndose la suma constante.

Fuerzas sobre la rueda

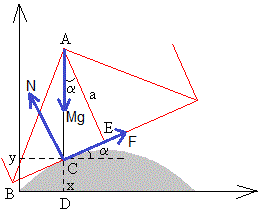
Las fuerzas que actúan sobre la rueda cuadrada son:

• El peso Mg en el centro de la rueda A
• La reacción N de la superficie en el punto de contacto C
• La fuerza de rozamiento F

Las ecuaciones del movimiento son:

• Equilibrio en la dirección vertical

Ncosα+Fsinα=Mg

• Dinámica de traslación en la dirección horizontal, siendo a_c la aceleración del centro de masas A

-Nsinα+Fcosα=Ma_c

• Dinámica de rotación alrededor de un eje perpendicular a la rueda y que pasa por su centro

N·atanα-F·a=I_c(dω/dt)

En el sistema de las dos primeras ecuaciones despejamos F y N

${\displaystyle \{\begin{array}{l}F=Mg\sin \alpha +M{a}_c\cos \alpha \\ N=Mg\cos \alpha -M{a}_c\sin \alpha \end{array}}$

Conocida la velocidad de traslación v del centro de la rueda y la velocidad angular de rotación dα/dt, calculamos la aceleración a_c del c.m. (véase el apartado Ecuación del movimiento)

${\displaystyle a_c=\frac{dv}{dt}=\frac{dv}{d\alpha }\frac{d\alpha }{dt}=-\frac{4}{3}\frac{E_k}{Ma}\sin \alpha {\cos }^2\alpha {\left(1+\frac{2}{3}{\cos }^2\alpha \right)}^{-2}}$

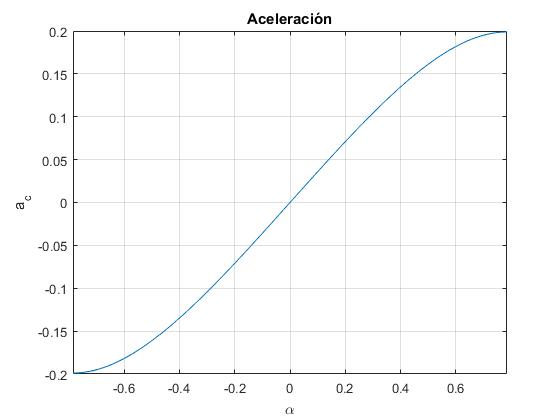
La aceleración a_c es proporcional a la energía cinética E_k, es máxima en los extremos α=-π/4 y α=π/4 y cero en el vértice α=0

f=@(alfa) (sin(alfa).*cos(alfa).^2)./(1+2*cos(alfa).^2/3).^2;
fplot(f,[-pi/4,pi/4])
grid on
xlabel('\alpha')
ylabel('a_c')
title('Aceleración')

Conocida la aceleración a_c, el valor de F y N es

${\displaystyle \begin{array}{l}F=Mg\sin \alpha \left\{1-\eta {\cos }^3\alpha {\left(1+\frac{2}{3}{\cos }^2\alpha \right)}^{-2}\right\}\\ N=Mg\cos \alpha \left\{1+\eta {\sin }^2\alpha \cos \alpha {\left(1+\frac{2}{3}{\cos }^2\alpha \right)}^{-2}\right\}\end{array}\}\eta =\frac{4E_k}{3Mga}}$

El movimiento de rodar sin deslizar se produce siempre que F≤μ_sN, siendo μ_s el coeficiente estático

${\displaystyle {\mu }_s\ge \frac{F}{N}=\frac{\sin \alpha \left({\left(1+\frac{2}{3}{\cos }^2\alpha \right)}^2-\eta {\cos }^3\alpha \right)}{\cos \alpha \left({\left(1+\frac{2}{3}{\cos }^2\alpha \right)}^2+\eta {\sin }^2\alpha \cos \alpha \right)}}$

hold on
for eta=[2,4,12]
    f=@(alfa) (sin(alfa).*((1+2*cos(alfa).^2/3).^2-(eta*cos(alfa).^3)))./
(cos(alfa).*((1+2*cos(alfa).^2/3).^2+eta*((sin(alfa).^2).*cos(alfa))));
    fplot(f,[-pi/4,pi/4], 'displayName',num2str(eta))
end
hold off
grid on
legend('-DynamicLegend','location','northeast')
xlabel('\alpha')
ylabel('F/N')
title('Rueda sin deslizar')

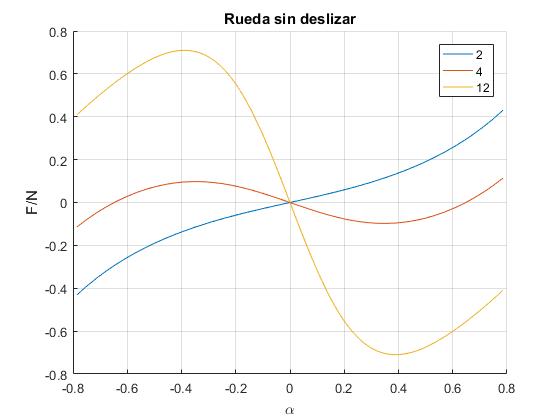
La fuerza de rozamiento F puede ser positiva o negativa, en el sentido inicado en la figura o en el contrario. Lo que nos interesa es su módulo

Cuando α=0, entonces F=0. Cuando η=0, para α=π/4, F/N=1, por lo que μ_s≥1. Como cabría esperar para que la rueda en reposo permanezca sin deslizar en el extremo de la catenaria, cuya pendiente es 45°

Para η=2, F/N crece hasta que alcanza el valor máximo 0.43 en el extremo del intervalo α=π/4. Este es el valor mínimo del coeficiente estático μ_s para que una rueda cuadrada cuya energía cinética es porporcional a 2 ruede sin deslizar.

Cuando la energía cinética de la rueda aumenta, η=12, observamos que F/N tiene un extremo 0.71 para el ángulo α=0.39. El valor mínimo del coeficiente estático será μ_s=0.71

El coeficiente estático mímimo μ_s para η=2 es mayor que para η=4, y es menor que para η=12. Habrá por tanto, un valor de η para el que μ_s presente un valor mínimo

La función F/N es monótona creciente, hasta cierto valor de η, alrededor de 1.7 en la que presenta un extremo. El valor mínimo del coeficiente estático es el valor de la función F/N en π/4

Cuando la función F/N presenta un extremo en el intervalo [0,π/4], su derivada en dicho intervalo es cero. El cálculo de la derivada y su simplificación es larga y tediosa, por lo que acudimos a Math Symbolic Toolbox de MATLAB para realizar esta tarea

>> syms x eta;
>> y=(sin(x)*((1+2*cos(x)^2/3)^2-eta*cos(x)^3))/(cos(x)*((1+2*cos(x)^2/3)^2+
eta*sin(x)^2*cos(x)));
>> z=simplify(diff(y))
 
z =(216*cos(x)^2 + 216*cos(x)^4 + 96*cos(x)^6 + 16*cos(x)^8 + 81*eta^2*cos(x)^4 - 
81*eta^2*cos(x)^6 + 162*eta*cos(x) - 243*eta*cos(x)^3 - 180*eta*cos(x)^5 
+ 36*eta*cos(x)^7 + 81)/(cos(x)^2*(4*cos(x)^4 - 9*eta*cos(x)^3 + 12*cos(x)^2 
+ 9*eta*cos(x) + 9)^2)

El comando latex(z) nos proporciona el código de esta expresión que podemos pegar en la ventana de MathType, después de hacer algunos arreglos, el resultado es

${\displaystyle z=\frac{-81{\eta }^2{\cos }^{6}x+81{\eta }^2{\cos }^{4}x+36\eta {\cos }^{7}x-180\eta \cos {\text{}}^{5}x-243\eta {\cos }^{3}x+162\eta \cos x+16\cos {\text{}}^{8}x+96{\cos }^{6}x+216{\cos }^{4}x+216{\cos }^{2}x+81}{{\cos }^{2}x{(4\cos {\text{}}^{4}x-9\eta {\cos }^3\text{}x+12{\cos }^{2}x+9\eta \cos x+9)}^2}}$

Solamente precisamos calcular la raíz del numerador de la fracción z(x), el ángulo x, para el cual la función y(x) presenta un extremo. Comparamos la ordenada de este extremo, si lo tuviese, con el valor de la función y(π/4). El mayor de los dos será el coeficiente estático mínimo

k=[0:0.1:1.5, 1.7:0.1:5];
mu=zeros(1,length(k));
for i=1:length(k)
    eta=k(i)^2;
   z =@(x) 216*cos(x)^2 + 216*cos(x)^4 + 96*cos(x)^6 + 16*cos(x)^8 + 
81*eta^2*cos(x)^4 - 81*eta^2*cos(x)^6 + 162*eta*cos(x) - 243*eta*cos(x)^3 
- 180*eta*cos(x)^5 + 36*eta*cos(x)^7 + 81;
   y=@(x) (sin(x)*((1+2*cos(x)^2/3)^2-eta*cos(x)^3))/(cos(x)*((1+2*cos(x)^2/3)^2+
eta*sin(x)^2*cos(x)));
   X=fzero(z, pi/8);
   if isnan(X)
       mu(i)=abs(y(pi/4));
   else
       if abs(y(X))>abs(y(pi/4))
           mu(i)=abs(y(X));
       else
            mu(i)=abs(y(pi/4));
       end
   end
end
plot(k,mu)
grid on
xlabel('sqrt(\eta)')
ylabel('\mu_m')
title('Coeficiente estático mínimo')

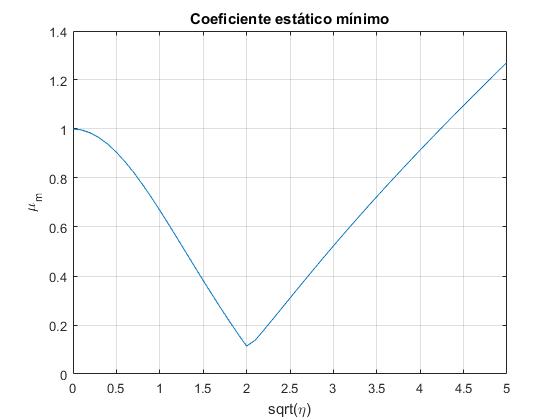
El script tiene dificultades para calcular los valores de los coeficientes estáticos mínimos, en el intervalo k=[1.5,1.7]. La imagen reproduce la figura 4 del segundo artículo citado en las referencias y confirma, que el mínimo de μ_s se encuentra alrededor de k=2, o η=4

Referencias

Klein N. Square wheel. Am. J. Phys. 61(10) October 1993, pp. 893-896.

Para el último apartado, Fuerzas sobre la rueda

L. Takacs. The square wheel revisited. Am. J. Phys. 62 (12) December 1994, pp. 1141-1144