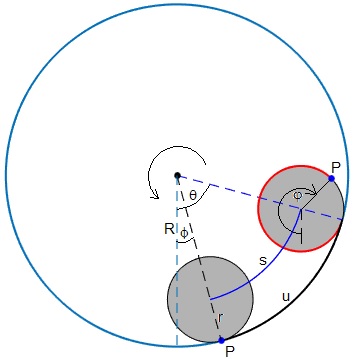
Un cuerpo cilíndrico de radio r rueda sin deslizar sobre la superficie interior de un tubo radio R. El tubo gira alrededor de su eje, en el instante t ha girado un ángulo ø, la posición angular del eje del cilindro es θ y la posición angular del punto P es φ

El centro del cilindro describe un arco s=(R-r)(θ-ø) (en color azul), mientras rueda una longitud u=R/=(θ-ø) sobre la pista (en color negro) e igual al arco de color rojo pintado sobre el cuerpo. La relación entre los ángulos es

${\displaystyle \phi =\frac{R\left(\theta -\varphi \right)}{r}-\theta =\frac{R-r}{r}\theta -\frac{R}{r}\varphi }$

Parte de la figura ha sido elaborada con el siguiente código

r=0.25; %radio del cuerpo que rueda
hold on
%pista
fplot(@(t) cos(t), @(t) sin(t), [0,2*pi], 'linewidth',1.5)
%cuerpo
ang=(1:360)*pi/180;
th=15*pi/180; %ángulo
x1=(1-r)*sin(th)+r*cos(ang);
y1=-(1-r)*cos(th)+r*sin(ang);
fill(x1,y1,[0.7 0.7 0.7])
line([0,sin(th)],[0,-cos(th)],'linestyle','--')
plot(0,0,'bo','linewidth',1,'markersize',4,'markeredgecolor','k',
'markerfacecolor','k')

th=60*pi/180; %ángulo
x1=(1-r)*sin(th)+r*cos(ang);
y1=-(1-r)*cos(th)+r*sin(ang);
fill(x1,y1,[0.7 0.7 0.7])
line([0,sin(th)],[0,-cos(th)],'linestyle','--','color','b')
fplot(@(t) (1-r)*sin(th)+r*cos(t), @(t) -(1-r)*cos(th)+r*sin(t),[-th/r-(pi/2-th)
,-(pi/2-th)], 'linewidth',1.5, 'color','r')
fplot(@(t) (1-r)*cos(t), @(t) (1-r)*sin(t), [-pi/2+pi/12,-(pi/2-th)],
 'linewidth',1,'color','b')
fplot(@(t) cos(t), @(t) sin(t), [-pi/2+pi/12,-(pi/2-th)], 'linewidth',
1.5,'color','k')
plot(sin(pi/12),-cos(pi/12),'bo','linewidth',1,'markersize',4,'markeredgecolor',
'b','markerfacecolor','b')
plot((1-r)*sin(th)+r*cos(-th/r-(pi/2-th)),-(1-r)*cos(th)+r*sin(-th/r-(pi/2-
th)),'bo','linewidth',1,'markersize',4,'markeredgecolor','b',
'markerfacecolor','b')
plot(0,0,'bo','linewidth',1,'markersize',4,'markeredgecolor','k',
'markerfacecolor','k')
line([0,sin(pi/12)],[0,-cos(pi/12)],'linestyle','--','color','k')
line([0,0],[0,-1],'linestyle','--')

hold off
axis equal
axis off

Ecuaciones del movimiento

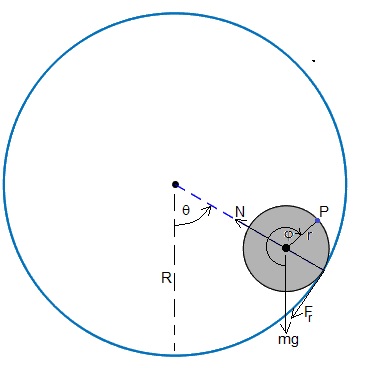
Sobre el cilindro actúan tres fuerzas

• El peso, mg
• la reacción N de la superficie del tubo en el punto de contacto
• La fuerza de rozamiento F_r que hace que el cilindro ruede sin deslizar por la superficie interior del tubo

Escribimos las ecuaciones del movimiento del cilindro y del tubo

• Movimiento del cilindro

• Movimiento de traslación del centro de masas

${\displaystyle m(R-r)\frac{d^2\theta }{d{t}^2}=-mg\sin \theta -F_r}$

• Movimiento de rotación alrededor del eje del cilindro

${\displaystyle \begin{array}{l}\left(\frac{1}{2}m{r}^2\right)\frac{d^2\phi }{d{t}^2}=F_{r}r\\ \left(\frac{1}{2}mr\right)\left(\frac{R-r}{r}\frac{d^2\theta }{d{t}^2}-\frac{R}{r}\frac{d^2\varphi }{d{t}^2}\right)=F_r\\ \left(\frac{1}{2}m\right)\left(\left(R-r\right)\frac{d^2\theta }{d{t}^2}-R\frac{d^2\varphi }{d{t}^2}\right)=F_r\end{array}}$

F_r es la fuerza que ejerce el tubo sobre el cilindro



• Movimiento de rotación del tubo alrededor de su eje fijo

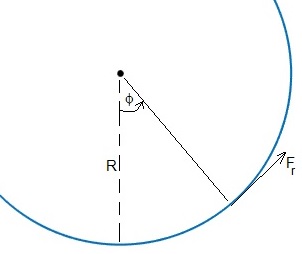
Por la tercera ley de Newton, la fuerza que el cilindro ejerce sobre el tubo F_r es igual y de sentido contrario.

${\displaystyle \left(M{R}^2\right)\frac{d^2\varphi }{d{t}^2}=F_{r}R}$

Tenemos un sistema de tres ecuaciones diferenciales. Entre las dos primeras eliminamos la fuerza de rozamiento F_r

${\displaystyle \begin{array}{l}(R-r)\frac{d^2\theta }{d{t}^2}=-g\sin \theta -\left(\frac{1}{2}\right)\left(\left(R-r\right)\frac{d^2\theta }{d{t}^2}-R\frac{d^2\varphi }{d{t}^2}\right)\\ \frac{3}{2}\left(R-r\right)\frac{d^2\theta }{d{t}^2}-\frac{1}{2}R\frac{d^2\varphi }{d{t}^2}+g\sin \theta =0\end{array}}$

Combinamos la segunda y tercera ecuación del movimiento

${\displaystyle \begin{array}{l}\left(\frac{1}{2}m\right)\left(\left(R-r\right)\frac{d^2\theta }{d{t}^2}-R\frac{d^2\varphi }{d{t}^2}\right)=MR\frac{d^2\varphi }{d{t}^2}\\ m\left(R-r\right)\frac{d^2\theta }{d{t}^2}-\left(m+2M\right)R\frac{d^2\varphi }{d{t}^2}=0\\ \frac{d}{dt}\left(m\left(R-r\right)\frac{d\theta }{dt}-\left(m+2M\right)R\frac{d\varphi }{dt}\right)=0\end{array}}$

Aparece una constante del movimiento que denominaremos J

${\displaystyle J=\left(m+2M\right)R\frac{d\varphi }{dt}-m\left(R-r\right)\frac{d\theta }{dt}}$

Energía del sistema

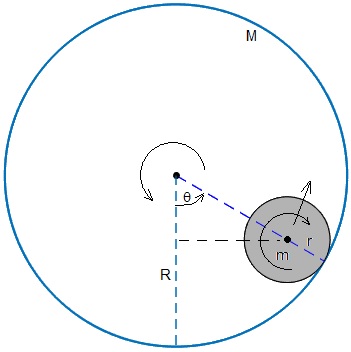
La energía del sistema formado por el cilindro y el tubo es constante

• Energía de rotación del tubo con velocidad angular dø/dt
• Energía de traslación del c.m. del cilindro con velocidad (R-r)dθ/dt y de rotación alrededor de su eje con velocidad angular dφ/dt
• Energía potencial del c.m. del cilindro referida al punto más bajo del tubo

${\displaystyle \begin{array}{l}E=\frac{1}{2}\left(M{R}^2\right){\left(\frac{d\varphi }{dt}\right)}^2+\frac{1}{2}\left(\frac{1}{2}m{r}^2\right){\left(\frac{d\phi }{dt}\right)}^2+\frac{1}{2}m{\left(R-r\right)}^2{\left(\frac{d\theta }{dt}\right)}^2+mg\left(R-r\right)\left(1-\cos \theta \right)\\ E=\frac{1}{2}\left(M{R}^2\right){\left(\frac{d\varphi }{dt}\right)}^2+\frac{1}{2}\left(\frac{1}{2}m{r}^2\right){\left(\frac{R-r}{r}\frac{d\theta }{dt}-\frac{R}{r}\frac{d\varphi }{dt}\right)}^2+\frac{1}{2}m{\left(R-r\right)}^2{\left(\frac{d\theta }{dt}\right)}^2+mg\left(R-r\right)\left(1-\cos \theta \right)\\ E=\frac{1}{4}\left(2M+m\right)R^2{\left(\frac{d\varphi }{dt}\right)}^2-\frac{1}{2}mR\left(R-r\right)\frac{d\theta }{dt}\frac{d\varphi }{dt}+\frac{3}{4}m{\left(R-r\right)}^2{\left(\frac{d\theta }{dt}\right)}^2+mg\left(R-r\right)\left(1-\cos \theta \right)\end{array}}$

Ecuaciones de Lagrange

Volvemos a obtener las ecuaciones del movimiento. La lagrangiana es

${\displaystyle \begin{array}{l}L=E_k-E_p(\theta )\\ L=\frac{1}{2}\left(M{R}^2\right){\left(\frac{d\varphi }{dt}\right)}^2+\frac{1}{2}\left(\frac{1}{2}m{r}^2\right){\left(\frac{d\phi }{dt}\right)}^2+\frac{1}{2}m{\left(R-r\right)}^2{\left(\frac{d\theta }{dt}\right)}^2-mg\left(R-r\right)\left(1-\cos \theta \right)\\ L=\frac{1}{4}\left(2M+m\right)R^2{\left(\frac{d\varphi }{dt}\right)}^2-\frac{1}{2}mR\left(R-r\right)\frac{d\theta }{dt}\frac{d\varphi }{dt}+\frac{3}{4}m{\left(R-r\right)}^2{\left(\frac{d\theta }{dt}\right)}^2-mg\left(R-r\right)\left(1-\cos \theta \right)\end{array}}$

La primera ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ -\frac{1}{2}mR\left(R-r\right)\frac{d^2\varphi }{d{t}^2}+\frac{3}{2}m{\left(R-r\right)}^2\frac{d^2\theta }{d{t}^2}+mg\left(R-r\right)\sin \theta =0\\ \frac{3}{2}\left(R-r\right)\frac{d^2\theta }{d{t}^2}-\frac{1}{2}R\frac{d^2\varphi }{d{t}^2}+g\sin \theta =0\end{array}}$

Como la lagrangiana L no depende de ø, hay una cantidad que se conserva

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\varphi }}\right)-\frac{\partial L}{\partial \varphi }=0\\ \frac{d}{dt}\left(\frac{1}{2}\left(2M+m\right)R^2\frac{d\varphi }{dt}-\frac{1}{2}mR\left(R-r\right)\frac{d\theta }{dt}\right)=0\\ \frac{d}{dt}\left(\left(2M+m\right)R\frac{d\varphi }{dt}-m\left(R-r\right)\frac{d\theta }{dt}\right)=0\\ J=\left(2M+m\right)R\frac{d\varphi }{dt}-m\left(R-r\right)\frac{d\theta }{dt}\end{array}}$

Movimiento del cilindro

En el sistema de dos ecuaciones

${\displaystyle \{\begin{array}{l}\frac{3}{2}\left(R-r\right)\frac{d^2\theta }{d{t}^2}-\frac{1}{2}R\frac{d^2\varphi }{d{t}^2}+g\sin \theta =0\\ \left(2M+m\right)R\frac{d^2\varphi }{d{t}^2}-m\left(R-r\right)\frac{d^2\theta }{d{t}^2}=0\end{array}}$

Eliminamos d²ø/dt²

${\displaystyle \frac{d^2\theta }{d{t}^2}+\left(\frac{2M+m}{3M+m}\right)\frac{g}{R-r}\sin \theta =0}$

El c.m. del cilindro se comporta como un péndulo simple, por lo que cabe esperar que describa oscilaciones o rotaciones, dependiendo de las condiciones iniciales

Cuando las oscilaciones son de pequeña amplitud, sinθ≈θ. El cilindro describe un Movimiento Armónico Simple de periodo

${\displaystyle P=2\pi \sqrt{\frac{R-r}{g}\left(\frac{m+3M}{m+2M}\right)}}$

La reacción N y la fuerza de rozamiento F_r

La ecuación del movimiento del cilindro en la dirección normal, véase la primera figura, es

${\displaystyle m{\left(\frac{d\theta }{dt}\right)}^2(R-r)=N-mg\cos \theta }$

De la ecuación del movimiento del c.m. del cilindro obtenemos F_r

${\displaystyle \begin{array}{l}m(R-r)\frac{d^2\theta }{d{t}^2}=-mg\sin \theta -F_r\\ \frac{d^2\theta }{d{t}^2}+\left(\frac{2M+m}{3M+m}\right)\frac{g}{R-r}\sin \theta =0\\ F_r=-mg\sin \theta +m(R-r)\left(\frac{2M+m}{3M+m}\right)\frac{g}{R-r}\sin \theta \\ F_r=-m\frac{M}{3M+m}g\sin \theta \end{array}}$

Se tiene que cumplir que la reacción N>0, y que el valor absoluto la fuerza de rozamiento |F_r|<μ_sN, sea menor que el valor máximo, en caso contrario el cilindro desliza

Ejemplos

Resolveremos el sistema de dos ecuaciones diferenciales

${\displaystyle \begin{array}{l}\frac{d^2\theta }{d{t}^2}=-\left(\frac{2M+m}{3M+m}\right)\frac{g}{R-r}\sin \theta =0\\ \frac{d\varphi }{dt}=\frac{J+m\left(R-r\right)}{\left(2M+m\right)R}\frac{d\theta }{dt}\end{array}}$

Con distintas condiciones iniciales, comprobaremos que la energía del sistema se mantiene constante

• Radio del tubo, R=1 m
• Radio del cilindro, r=0.25 m
• Masa del tubo, M=1 kg
• Masa del cilindro, m=2 kg

En el instante t=0

• Posición angular del tubo, ø=0, velocidad angular, dø/dt=0
• Posición angular del cilindro, θ=0, velocidad angular, dθ/dt=1. Velocidad angular de rotación dφ/dt=0

Se le proporciona una velocidad inicial al cilindro

R=1; %radio del tubo
r=0.4; %radio del cilindro
M=1; %masa del tubo
m=2; %masa del cilindro

w2=(2*M+m)*9.8/((3*M+m)*(R-r));
vx=1; vy=0;
J=(2*M+m)*R*vy-m*(R-r)*vx;
f=@(t,x) [x(2);-w2*sin(x(1)); (J+m*(R-r)*x(2))/((2*M+m)*R)]; 
[t,x]=ode45(f,[0,5],[0,vx,0]);
hold on
plot(t,x(:,1)) %cilindro macizo
plot(t,x(:,3)) %tubo
hold off
grid on
xlabel('t')
ylabel('\theta')
legend('cilindro','tubo','location','best')
title('Movimiento del cilindro')
%energía
E_ini=3*m*(R-r)^2*vx^2/4;
vy=(J+m*(R-r)*x(:,2))/((m+2*M)*R);
E=(2*M+m)*R*R*vy.^2/4-m*R*(R-r)*vy.*x(:,2)/2+3*m*(R-r)^2*x(:,2).^2/4
+m*9.8*(R-r)*(1-cos(x(:,1)));

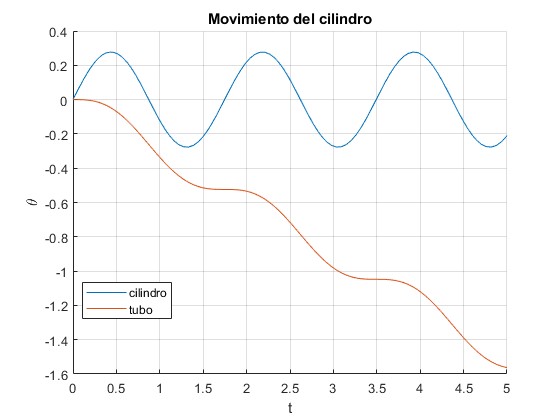
Observamos oscilaciones de pequeña delcilindro alrededor de la posición θ=0. Mientras, el tu gira en el sentido de las agujas del reloj. Comprobamos que el periodo de las oscilaciones aproximadamente coincide con la aproximación sinθ≈θ

Comprobamos que la energía se mantiene constante

>> E_ini
E_ini =    0.5400
>> E
E = 0.5400
    0.5400
    .....
    0.5396
    0.5394

En el instante t=0

• Posición angular del tubo, ø=0, velocidad angular, dø/dt=0
• Posición angular del cilindro, θ=π/3 (60°), velocidad angular, dθ/dt=0. Velocidad angular de rotación dφ/dt=0

Desplazamos el cilindro un ángulo de 60° y lo soltamos

R=1; %radio del tubo
r=0.4; %radio del cilindro
M=1; %masa del tubo
m=2; %masa del cilindro

w2=(2*M+m)*9.8/((3*M+m)*(R-r));
th_0=pi/3;
J=0;
f=@(t,x) [x(2);-w2*sin(x(1)); (J+m*(R-r)*x(2))/((2*M+m)*R)]; 
[t,x]=ode45(f,[0,5],[th_0,0,0]);
hold on
plot(t,x(:,1)) %cilindro macizo
plot(t,x(:,3)) %tubo
hold off
grid on
xlabel('t')
ylabel('\theta')
legend('cilindro','tubo','location','best')
title('Movimiento del cilindro')
%energía
E_ini=m*9.8*(R-r)*(1-cos(th_0));
J=0;
vy=(J+m*(R-r)*x(:,2))/((m+2*M)*R);
E=(2*M+m)*R*R*vy.^2/4-m*R*(R-r)*vy.*x(:,2)/2+3*m*(R-r)^2*x(:,2).^2/4
+m*9.8*(R-r)*(1-cos(x(:,1)));

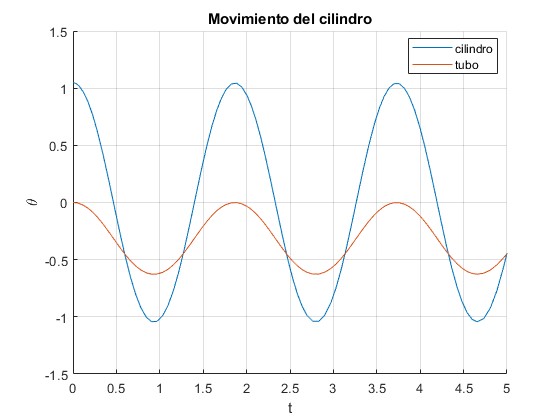
Observamos oscilaciones del cilindro y del tubo. Comprobamos que la energía se matiene constante

>> E_ini
E_ini =    5.8800
>> E
E = 5.8800
    5.8800
    ....
    5.8424
    5.8424

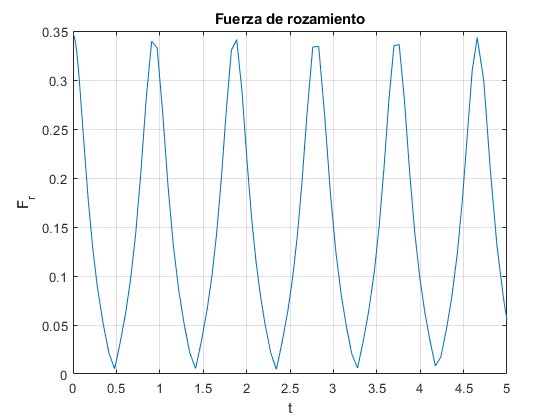
Representamos el cociente entre el valor absoluto de la fuerza de rozamiento y la reacción del tubo, |F_r|/N en función del tiempo t. Vemos que si el coeficiente estático es mayor que 0.35, el cilindro rueda sin deslizar

R=1; %radio del tubo
r=0.4; %radio del cilindro
M=1; %masa del tubo
m=2; %masa del cilindro

w2=(2*M+m)*9.8/((3*M+m)*(R-r));
th_0=pi/3;
J=0;
f=@(t,x) [x(2);-w2*sin(x(1)); (J+m*(R-r)*x(2))/((2*M+m)*R)]; 
[t,x]=ode45(f,[0,5],[th_0,0,0]);
Fr=abs(-m*M*9.8*sin(x(:,1))/(3*M+m));
N=m*9.8*cos(x(:,1))+m*x(:,2).^2*(R-r);
plot(t,Fr./N)
grid on
xlabel('t')
ylabel('F_r')
title('Fuerza de rozamiento')

Actividades

Se introduce

• La masa del cilindro, m, en el control titulado Masa cilindro
• El radio del cilindro, r, en el control titulado Radio
• La masa del tubo se ha fijado en M=1 kg
• El radio del tubo se ha fijado en R=1 m
• La posición angular inicial (en grados) del cilindro en el control titulado Posición
• La velocidad inicial (en rad/s) del c. m. del cilindro en el control titulado Velocidad
• La velocidad angular inicial de rotación del cilindro dφ/dt=0
• Se ha fijado la posición angular ø=0 y la velocidad angular inicial de rotación del tubo dø/dt=0

Se pulsa el botón titulado Nuevo

Observamos el movimiento de rotación del tubo y al cilindro rodando sin deslizar por el interior del tubo

En la parte derecha, se proporcionan los datos del

• El tiempo t en s
• La posición angular θ del c.m. del cilindro
• La velocidad angular dθ/dt del c. m. del cilindro
• La posición angular ø del tubo
• La reacción N del tubo

El programa calcula en cada instante el tanto por ciento de error relativo en la energía o el cociente

${\displaystyle \left|\frac{E-E_0}{E_0}\right|·100}$

donde E es la energía del sistema en cualquier instante t, y E₀ es la energía inicial del sistema.

Este valor se proporciona en caracteres de color rojo en la parte inferior derecha. Su valor debe ser siempre cero, o un valor muy pequeño lo que indica que la energía del sistema permanece constante y el programa realiza los cálculos correctamente.

Cuando la reacción N≤0 del tubo, la animación se detiene

Referencias

APhO Problems and Solutions, 2009 Thailand. Rolling Cylinders