Superficie cilíndrica convexa

En la página titulada Oscilaciones de un cuerpo que rueda sobre superficie cóncava, estudiamos el movimiento de un cuerpo que rueda sin deslizar sobre una superficie cilíndrica cóncava

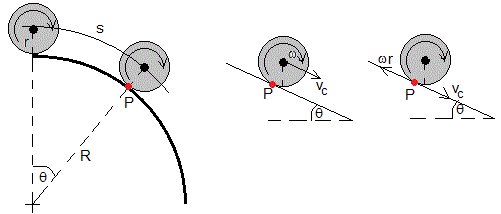
Como hemos demostrado, para que un cuerpo en forma de aro, cilindro o esfera de radio r, ruede sin deslizar en un plano horizontal o inclinado, se tiene que cumplir que v_c=ωr, a fin de que la velocidad del punto P de contacto del cuerpo con el plano sea nula. Donde

• v_c es la velocidad del centro de masas
• ω es la velocidad angular de rotación alrededor de un eje que pasa por el centro

En el caso de que el cuerpo ruede sobre una superficie cilíndrica, la velocidad del centro de masas es

${\displaystyle v_c=\frac{ds}{dt}=(R+r)\frac{d\theta }{dt}}$

La velocidad angular de rotación es

${\displaystyle \omega =\frac{d\phi }{dt}}$

Para que la velocidad del punto P de contacto sea nula, se tiene que cumplir que

${\displaystyle (R+r)\frac{d\theta }{dt}=r\frac{d\phi }{dt}}$

La relación entre el desplazamiento angular del centro del cuerpo θ y el ángulo φ girado por el cuerpo es (R+r)θ=rφ

Vamos a comprobar esta relación de forma geométrica

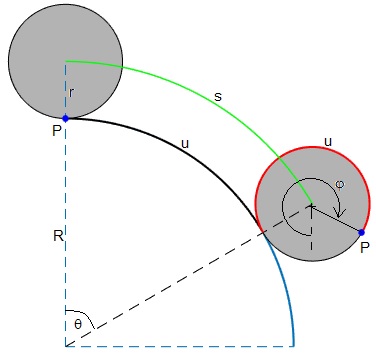
Un cuerpo de radio r rueda sin deslizar sobre una superficie cilíndrica de radio R. El centro del cuerpo describe un arco s=(R+r)θ (en color verde), mientras el cuerpo rueda una longitud u=Rθ sobre la pista (en color negro) e igual al arco de color rojo pintado sobre el cuerpo. la posición angular del punto P del cuerpo, como vemos en la figura es, φ=u/r+θ o bien, (R+r)θ=rφ

${\displaystyle \phi =\frac{R+r}{r}\theta }$

Parte de la figura ha sido elaborada con el siguiente código

th=pi/3; %ángulo
r=0.25; %radio del cuerpo que rueda
hold on
fplot(@(t) cos(t), @(t) sin(t), [0, pi/2], 'linewidth',1.5)
ang=(1:360)*pi/180;
x1=r*cos(ang);
y1=(1+r)+r*sin(ang);
fill(x1,y1,[0.7 0.7 0.7])
line([0,0],[0,1+r],'linestyle','--')
line([0,1],[0,0],'linestyle','--')

x1=(1+r)*sin(th)+r*cos(ang);
y1=(1+r)*cos(th)+r*sin(ang);
fill(x1,y1,[0.7 0.7 0.7])
line([0,(1+r)*sin(th)],[0,(1+r)*cos(th)],'linestyle','--','color','k')
fplot(@(t) cos(t), @(t) sin(t), [pi/2-th,pi/2,], 'linewidth',1.5,'color','k')
fplot(@(t) (1+r)*sin(th)+r*cos(t), @(t) (1+r)*cos(th)+r*sin(t), 
[-th/r-(pi/2+th),-(pi/2+th)], 'linewidth',1.5, 'color','r')
fplot(@(t) (1+r)*cos(t), @(t) (1+r)*sin(t), [pi/2-th, pi/2], 
'linewidth',1,'color','g')
plot(0,1,'bo','linewidth',1,'markersize',4,'markeredgecolor',
'b','markerfacecolor','b')
plot((1+r)*sin(th)+r*cos(-th/r-(pi/2+th)),(1+r)*cos(th)+
r*sin(-th/r-(pi/2+th)),'bo','linewidth',1,'markersize',4,'markeredgecolor',
'b','markerfacecolor','b')

hold off
axis equal
axis off

Movimiento de la esfera

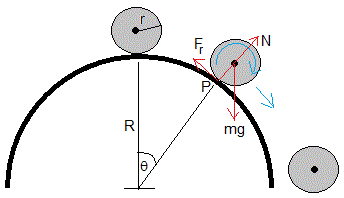
La cúpula semiesférica tiene un radio R, y la esfera tiene un radio r. Se sitúa la esfera en el origen, en el vértice de la cúpula, θ=0. Cuando el centro de la esfera se ha desplazado un ángulo θ, las fuerzas que actúan son:

• El peso, mg
• La reacción N o fuerza que ejerce la cúpula sobre la esfera
• La fuerza de rozamiento F_r

Etapas del movimiento:

• Cuando F_r<μN la esfera rueda sin deslizar sobre la cúpula
• Cuando F_r=μN la esfera rueda y desliza
• Cuando N=0, la esfera deja de tener contacto con la cúpula. El centro de la esfera describe un movimiento parabólico hasta que impacta en el suelo.

La esfera rueda sin deslizar

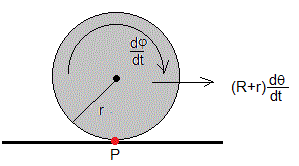
Para que la esfera ruede si deslizar, el punto P de contacto de la esfera con la cúpula tiene que tener velocidad cero, lo que implica una relación entre la velocidad de traslación y la velocidad angular de rotación

${\displaystyle \begin{array}{l}\left(R+r\right)\frac{d\theta }{dt}=r\frac{d\phi }{dt}\\ \left(R+r\right)\theta =r\phi \end{array}}$

O bien, una relación entre el ángulo θ que se desplaza el centro de la esfera y el ángulo φ que gira la esfera. Se supone que en el instante t=0, θ=0 y φ=0.

Principio de conservación de la energía

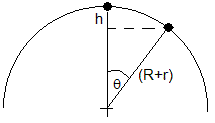
A medida que la esfera rueda sin deslizar, disminuye la energía potencial del centro de la esfera (punto de color negro en la figura) correspondiente a una altura h=(R+r)-(R+r)cosθ

Como consecuencia, se incrementa la energía cinética de traslación del centro de masa (c.m.) de la esfera y la energía cinética de rotación alrededor de un eje que pasa por el c.m. El momento de inercia de la esfera de masa m y radio r es 2mr²/5.

${\displaystyle mg(R+r)-mg(R+r)\cos \theta =\frac{1}{2}m{\left((R+r)\frac{d\theta }{dt}\right)}^2+\frac{1}{2}\left(\frac{2}{5}m{r}^2\right){\left(\frac{d\phi }{dt}\right)}^2}$

Teniendo en cuenta la relación entre la velocidad angular de traslación dθ/dt y la de rotación dφ/dt, despejamos dθ/dt

${\displaystyle \begin{array}{l}{\left(\frac{d\theta }{dt}\right)}^2=\frac{10g}{7(R+r)}(1-\cos \theta )\\ \frac{d\theta }{dt}=2\sqrt{\frac{5g}{7(R+r)}}\sin \frac{\theta }{2}\end{array}}$

Ecuaciones del movimiento

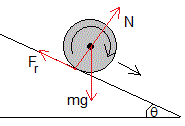
En la figura, se representan las fuerzas sobre la esfera

• Movimiento de traslación del centro de masa

${\displaystyle m(R+r)\frac{d^2\theta }{d{t}^2}=mg\sin \theta -F_r}$

• Movimiento de rotación alrededor de un eje que pasa por el c.m

${\displaystyle \left(\frac{2}{5}m{r}^2\right)\frac{d^2\phi }{d{t}^2}=F_r·r}$

Si la esfera rueda sin deslizar, ambas aceleraciones están relacionadas (R+r)θ=rφ. Despejamos la fuerza de rozamiento F_r del sistema de ecuaciones

${\displaystyle F_r=\frac{2}{7}mg\sin \theta }$

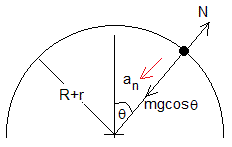
El centro de la esfera describe una arco de circunferencia de radio (R+r) con velocidad (R+r)dθ/dt. Aplicamos la ecuación de la dinámica del movimiento circular,

${\displaystyle \begin{array}{l}m(R+r){\left(\frac{d\theta }{dt}\right)}^2=mg\cos \theta -N\\ N=\frac{mg}{7}\left(17\cos \theta -10\right)\end{array}}$

Si la esfera rodase sin deslizar, la reacción N se haría cero para el ángulo cosθ_n=10/17. Para una partícula obtuvimos cosθ_n=2/3

Final de la primera etapa

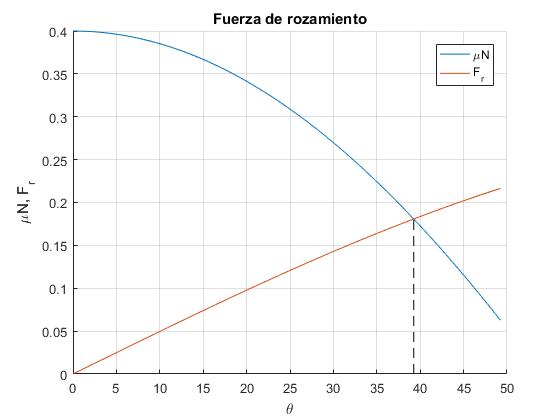
En la figura, representamos F_r y μN en función del ángulo θ. Para el ángulo θ tal que F_r=μN la esfera empieza a deslizar. Este ángulo está señalado en la figura mediante una línea vertical a trazos

${\displaystyle \begin{array}{l}\frac{2}{7}mg\sin \theta =\mu \frac{mg}{7}\left(17\cos \theta -10\right)\\ 2\sin \theta -17\mu \cos \theta +10\mu =0\end{array}}$

Se puede expresar como ecuación de segundo grado en cosθ

${\displaystyle \begin{array}{l}(289{\mu }^2+4){\cos }^2\theta -340{\mu }^2\cos \theta +100{\mu }^2-4=0\\ \cos {\theta }_s=\frac{170{\mu }^2+2\sqrt{189{\mu }^2+4}}{289{\mu }^2+4}\end{array}}$

En este ejemplo, la cúpula tiene un radio R=1 y el coeficiente de rozamiento μ=0.4

R=1; %radio
mu=0.4; %coef. rozamiento

aDesliza=acos((170*mu^2+2*sqrt(189*mu^2+4))/(289*mu^2+4))*180/pi;
muN=@(x) mu*(17*cos(x*pi/180)-10)/7;
Fr=@(x) 2*sin(x*pi/180)/7;

hold on
fplot(muN,[0,aDesliza+10])
fplot(Fr,[0,aDesliza+10])
line([aDesliza,aDesliza], [0,Fr(aDesliza)], 'LineStyle','--','color','k')
hold off

grid on
xlabel('\theta')
ylabel('\muN, F_r');
legend('\muN', 'F_r')
title('Fuerza de rozamiento')

>> aDesliza
ans =   39.2545

Este ángulo límite θ_s se incrementa con el coeficiente de rozamiento μ, tal como vemos en la figura más abajo

f=@(x) acos((170*x.^2+2*sqrt(189*x.^2+4))./(289*x.^2+4))*180/pi;
fplot(f,[0,1])
grid on
xlabel('\mu')
ylabel('\theta_s')
title('Empieza a deslizar')

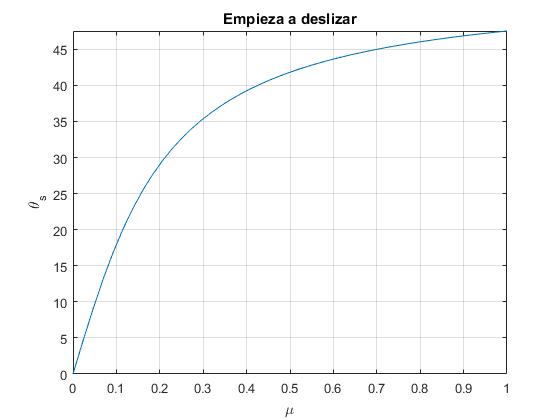
Para este ángulo límite θ_s, el cuadrado de la velocidad angular (dθ/dt)_s de traslación del c.m. de la esfera es

${\displaystyle {\left(\frac{d\theta }{dt}\right)}_s^2=\frac{10g}{7(R+r)}(1-\cos {\theta }_s)}$

Caso particular: no hay rozamiento μ=0

Si el rozamiento fuera nulo μ=0, entonces cosθ_s=1, θ_s=0, no tendríamos movimiento de rotación, solamente de traslación, el principio de conservación de la energía se escribiría

${\displaystyle \begin{array}{l}mg(R+r)-mg(R+r)\cos \theta =\frac{1}{2}m{\left((R+r)\frac{d\theta }{dt}\right)}^2\\ {\left(\frac{d\theta }{dt}\right)}^2=\frac{2g}{(R+r)}(1-\cos \theta )\end{array}}$

La reacción de la cúpula N valdría

${\displaystyle \begin{array}{l}m(R+r){\left(\frac{d\theta }{dt}\right)}^2=mg\cos \theta -N\\ N=3mg\cos \theta -2mg\end{array}}$

N se hace cero para el ángulo cosθ_s=2/3, que corresponde a un ángulo de 48° con la vertical, tal como ya hemos calculado al estudiar el movimiento de una partícula que desliza sin rozamiento sobre la cúpula.

La esfera rueda y desliza

Cuando θ>θ_s la esfera rueda y desliza, la fuerza de rozamiento alcanza su valor máximo, F_r=μN. Las ecuaciones del movimiento son:

• Movimiento de traslación del centro de masa

${\displaystyle m(R+r)\frac{d^2\theta }{d{t}^2}=mg\sin \theta -\mu N}$

• Movimiento de rotación alrededor de un eje que pasa por el c.m.

${\displaystyle \left(\frac{2}{5}m{r}^2\right)\frac{d^2\phi }{d{t}^2}=\mu N·r}$

No hay relación entre el movimiento de traslación y rotación

El centro de la esfera describe una arco de circunferencia de radio (R+r) con velocidad (R+r)dθ/dt. Aplicamos la ecuación de la dinámica del movimiento circular,

${\displaystyle mg\cos \theta -N=m(R+r){\left(\frac{d\theta }{dt}\right)}^2}$

Eliminamos N entre la primera y la tercera ecuación, y procedemos de forma similar al estudio del movimiento de una partícula que desliza con rozamiento sobre un cúpula semicircular

${\displaystyle m(R+r)\frac{d^2\theta }{d{t}^2}=mg\sin \theta -\mu \left(mg\cos \theta -m(R+r){\left(\frac{d\theta }{dt}\right)}^2\right)}$

Teniendo en cuenta que

${\displaystyle \frac{d^2\theta }{d{t}^2}=\frac{d\omega }{dt}=\frac{d\omega }{d\theta }\frac{d\theta }{dt}=\omega \frac{d\omega }{d\theta }=\frac{1}{2}\frac{d{\omega }^2}{d\theta }\omega =\frac{d\theta }{dt}}$

Se transforma una ecuación diferencial de segundo orden en otra de primero.

${\displaystyle \begin{array}{l}\frac{1}{2}\frac{d{\omega }^2}{d\theta }-\mu {\omega }^2=\frac{g}{(R+r)}\left(\sin \theta -\mu \cos \theta \right)\\ \frac{1}{2}\frac{dz}{d\theta }-\mu z=\frac{g}{(R+r)}\left(\sin \theta -\mu \cos \theta \right)\end{array}}$

con z=ω². La solución de la ecuación diferencial se compone de dos términos:

La solución particular z₁=Asinθ+Bcosθ

Introduciendo la solución particular en la ecuación diferencial obtenemos los valores de los coeficientes A y B

${\displaystyle A=\frac{-6\mu }{4{\mu }^2+1}\frac{g}{(R+r)}B=\frac{4{\mu }^2-2}{4{\mu }^2+1}\frac{g}{(R+r)}}$

Buscamos la solución de la ecuación diferencial homogénea

${\displaystyle \frac{1}{2}\frac{dz}{d\theta }-\mu z=0\frac{dz}{z}=2\mu ·d\theta {\displaystyle \int \frac{dz}{z}={\displaystyle \int 2\mu ·d\theta }}}$

Integrando ambos miembros obtenemos lnz=2μθ+cte, o bien, z₂=C·exp(2μθ)

La solución completa es z=z₁+z₂

${\displaystyle z=C\exp (2\mu \theta )+\frac{g}{(R+r)}\frac{-6\mu ·\text{sin}\theta +(4{\mu }^2-2)\cos \theta }{4{\mu }^2+1}}$

La constante C se determina a partir de las condiciones iniciales, para θ=θ_s, dθ/dt=(dθ/dt)_s

Finalmente, la ecuación que nos proporciona el cuadrado de la velocidad angular (dθ/dt)² en función del ángulo θ, es

${\displaystyle {\left(\frac{d\theta }{dt}\right)}^2=\frac{g}{(R+r)}\left\{\begin{array}{l}\exp \left(2\mu (\theta -{\theta }_s)\right)\left(\frac{10}{7}-\frac{68{\mu }^2-4}{7(4{\mu }^2+1)}\cos {\theta }_s+\frac{6\mu }{4{\mu }^2+1}\sin {\theta }_s\right)\\ -\frac{6\mu }{4{\mu }^2+1}\text{sin}\theta +\frac{(4{\mu }^2-2)}{4{\mu }^2+1}\cos \theta \end{array}\right\}}$

Ahora, calculamos la reacción N de la cúpula

${\displaystyle N=mg\cos \theta -m(R+r){\left(\frac{d\theta }{dt}\right)}^2}$

N se hace cero para el ángulo crítico θ_n tal que

${\displaystyle \begin{array}{l}3\cos \theta +6\mu \sin \theta \\ -\exp \left(2\mu (\theta -{\theta }_s)\right)\left\{\frac{10}{7}(4{\mu }^2+1)-\frac{68{\mu }^2-4}{7}\cos {\theta }_s+6\mu \sin {\theta }_s\right\}=0\end{array}}$

En este ejemplo, representamos la reacción N en función del ángulo θ>θ_s. La cúpula tiene un radio R=1 y el coeficiente de rozamiento μ=0.4. Calculamos el ángulo crítico θ_n para el cual N=0, conocido θ_s=39.25°

R=1; %radio
mu=0.4; %coef. rozamiento
aDesliza=acos((170*mu^2+2*sqrt(189*mu^2+4))/(289*mu^2+4));

N=@(x) cos(x*pi/180)-exp(2*mu*(x*pi/180-aDesliza))*
(10/7-(68*mu^2-4)*cos(aDesliza)/(28*mu^2+7)+6*mu*sin(aDesliza)/(4*mu^2+1))
+6*mu*sin(x*pi/180)/(4*mu^2+1)-(4*mu^2-2)*cos(x*pi/180)/(4*mu^2+1);
hold on
fplot(N,[aDesliza,pi/2]*180/pi)
f=@(x) 3*cos(x)+6*mu*sin(x)-(10*(4*mu^2+1)/7-(68*mu^2-4)*cos(aDesliza)/7
+6*mu*sin(aDesliza))*exp(2*mu*(x-aDesliza));
aNormal=fzero(f,aDesliza)*180/pi;

line([aNormal,aNormal], [-2.5,0], 'LineStyle','--','color','k')
hold off
grid on
xlabel('\theta')
ylabel('N')
title('Reacción N')

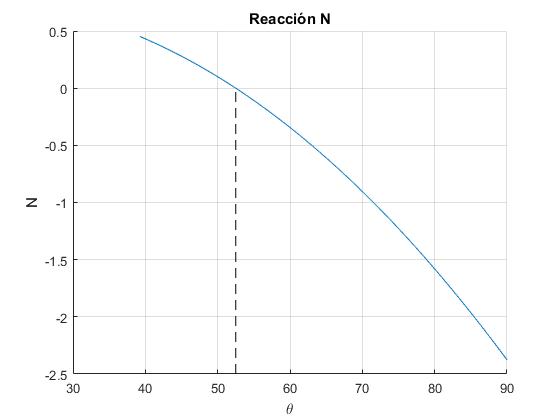
>> aNormal =   52.5008

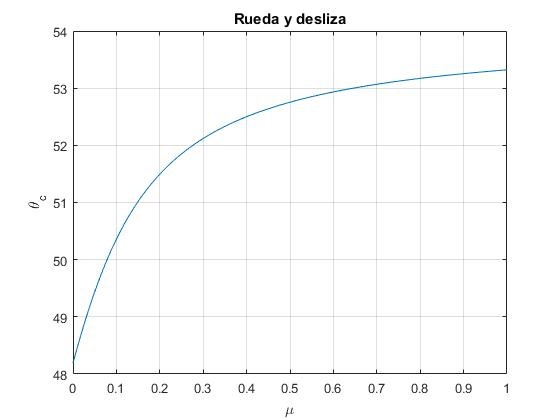
En la figura, se representa el ángulo θ_n en función del coeficiente de rozamiento μ. Este ángulo crece a partir de 48° cuando μ=0

g=@(x) acos((170*x.^2+2*sqrt(189*x.^2+4))./(289*x.^2+4));
roza=0:0.01:1;
k=0;
aNormal=zeros(1,length(roza));

for mu=roza
   aDesliza=g(mu); %ángulo límite rueda y desliza
    f=@(x) 3*cos(x)+6*mu*sin(x)-(10*(4*mu^2+1)/7-(68*mu^2-4)*cos(aDesliza)/7
+6*mu*sin(aDesliza))*exp(2*mu*(x-aDesliza));
    k=k+1;
    aNormal(k)=fzero(f,[aDesliza,pi/2]); %ángulo límite, N=0 
end
plot(roza,aNormal*180/pi)
grid on
xlabel('\mu')
ylabel('\theta_c')
title('Rueda y desliza')

Movimiento completo

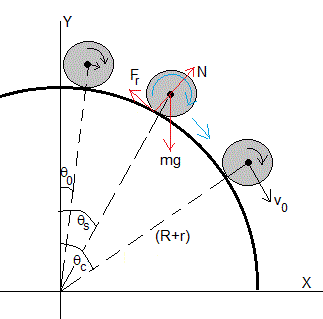
En este apartado, describiremos el movimiento del c.m. de la esfera cuya posición angular es θ. En la figura, se muestran las etapas del movimiento de la esfera sobre la cúpula

• La posición inicial de partida, desviado un pequeño ángulo θ₀ de la posición de equilibrio inestable θ=0
• Mientras la esfera está en contacto con la cúpula pueden ocurrir dos casos:
• La esfera rueda sin deslizar, la fuerza de rozamiento F_r es menor que el valor máximo μN en el intervalo entre θ₀ y θ_s
• La fuerza de rozamiento F_r=μN y la esfera rueda y desliza, en el intervalo entre θ_s y θ_n, para este ángulo N=0
• La esfera deja de estar en contacto con con la cúpula y su centro describe una trayectoria parabólica hasta que impacta en el suelo

El estado inicial

Para que comience el movimiento de la esfera, hemos de desviarla un pequeño ángulo θ₀ de su posición de equilibrio inestable θ=0. Aplicando el principio de conservación de la energía calculamos la velocidad inicial de traslación del c.m. para este ángulo inicial

${\displaystyle {\left(\frac{d\theta }{dt}\right)}_0=2\sqrt{\frac{5g}{7(R+r)}}\sin \frac{{\theta }_0}{2}}$

Rueda sin deslizar

Dado el coeficiente de rozamiento μ, calculamos el ángulo límite θ_s. Entre θ₀ y θ_s la esfera rueda sin deslizar

${\displaystyle \cos {\theta }_s=\frac{170{\mu }^2+2\sqrt{189{\mu }^2+4}}{289{\mu }^2+4}}$

Resolvemos aplicando procedimientos numéricos la ecuación diferencial que describe la posición angular θ del c.m. en función del tiempo t, con las condiciones iniciales especificadas, en el instante t=0, la posición inicial del c.m. es θ₀ y la velocidad angular inicial es (dθ/dt)₀

${\displaystyle (R+r)\frac{d^2\theta }{d{t}^2}=\frac{5}{7}g\sin \theta }$

En este ejemplo, representamos la posición angular θ en función del tiempo t. La cúpula tiene un radio R=1, la esfera tiene radio r=0.3 y el coeficiente de rozamiento μ=0.4. La posición inicial de partida es θ₀=0.01 rad

R=1; %radio
mu=0.4; %coef. rozamiento
r=0.3; %radio de la esfera
aDesliza=acos((170*mu^2+2*sqrt(189*mu^2+4))/(289*mu^2+4)); %ángulo límite

%posición inicial y velocidad inicial del c.m.
x0=[0.01,sqrt(980/R)*2*sin(0.01/2)]; 
f=@(t,x) [x(2);9.8*5*sin(x(1))/(7*(R+r))]; 
opts=odeset('events',@(t,x) stop_cupula_esfera(t,x,aDesliza));
tspan=[0,100]; 
[t,x]=ode45(f,tspan,x0,opts);
tFin=t(end);
hold on
plot(t,x(:,1)*180/pi)
... %continúa

El procedimiento de cálculo se detiene cuando la posición angular θ del c.m. alcanza el ángulo límite θ_s, definiendo la función

function [value,isterminal,direction]=stop_cupula_esfera(~,x,xFin)
    value=x(1)-xFin; 
    isterminal=1;
    direction=0; 
end

Al finalizar la primera etapa, la posición angular del c.m. de la esfera es θ_s y la velocidad angular es

${\displaystyle {\left(\frac{d\theta }{dt}\right)}_s=2\sqrt{\frac{5g}{7(R+r)}}\sin \frac{{\theta }_s}{2}}$

Rueda y desliza

Calculamos el ángulo límite θ_n para el cual la rueda deja de tener contacto con la cúpula, la reacción N=0, resolviendo la ecuación transcendente

${\displaystyle \begin{array}{l}3\cos \theta +6\mu \sin \theta \\ -\exp \left(2\mu (\theta -{\theta }_s)\right)\left\{\frac{10}{7}(4{\mu }^2+1)-\frac{68{\mu }^2-4}{7}\cos {\theta }_s+6\mu \sin {\theta }_s\right\}=0\end{array}}$

En el intervalo angular entre θ_s y θ_n, la esfera rueda y desliza, la ecuación del movimiento del c.m. de la esfera es

${\displaystyle (R+r)\frac{d^2\theta }{d{t}^2}=g\sin \theta -\mu \left(g\cos \theta -(R+r){\left(\frac{d\theta }{dt}\right)}^2\right)}$

Se resuelve aplicando procedimientos numéricos con las condiciones iniciales señaladas en el apartado anterior: la posición inicial del c.m. de la esfera es θ_s y su velocidad inicial (dθ/dt)_s.

....
 %ángulo límite, rueda sin deslizar
aDesliza=acos((170*mu^2+2*sqrt(189*mu^2+4))/(289*mu^2+4)); 
wDesliza=sqrt(10*9.8*(1-cos(aDesliza))/(7*(R+r)));

f=@(x) 3*cos(x)+6*mu*sin(x)-(10*(4*mu^2+1)/7-(68*mu^2-4)*cos(aDesliza)/7
+6*mu*sin(aDesliza))*exp(2*mu*(x-aDesliza));
aNormal=fzero(f,aDesliza); %ángulo límite para N=0

x0=[aDesliza,wDesliza];
f=@(t,x) [x(2); 9.8*sin(x(1))/(R+r)-mu*(9.8*cos(x(1))/(R+r)-x(2)^2)]; 
opts=odeset('events',@(t,x) stop_cupula_esfera(t,x,aNormal));
tspan=[0,100]; %hasta un tiempo de 3
[t,x]=ode45(f,tspan,x0,opts);
plot(t+tFin,x(:,1)*180/pi)
line([0,tFin], [aDesliza,aDesliza]*180/pi, 'LineStyle','--','color','k')
line([0,tFin+t(end)], [aNormal,aNormal]*180/pi, 'LineStyle','--','color','k')
line([tFin,tFin], [0,aDesliza]*180/pi, 'LineStyle','--','color','k')
line([tFin+t(end),tFin+t(end)], [0,aNormal]*180/pi, 'LineStyle','--','color','k')

hold off
grid on
xlabel('t')
ylabel('\theta');
title('Posición angular en función del tiempo')

El procedimiento de cálculo se detiene cuando la posición angular θ del c.m. alcanza el ángulo límite θ_n

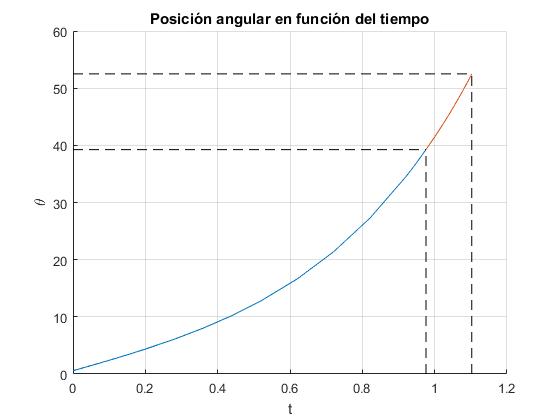
En color azul, se representa la primera etapa del movimiento: la esfera rueda sin deslizar. En color anaranjado, la segunda etapa: la esfera rueda y desliza, se señalan los instantes y los ángulos θ_s y θ_n

El ángulo límite es θ_n=52.5°. Comprobamos que la normal N para este ángulo es próxima a cero

>> w_c=sqrt(9.8*(exp(2*mu*(aNormal-aDesliza))*
(10/7-(68*mu^2-4)*cos(aDesliza)/(28*mu^2+7)+6*mu*sin(aDesliza)/(4*mu^2+1))-
6*mu*sin(aNormal)/(4*mu^2+1)+(4*mu^2-2)*cos(aNormal)/(4*mu^2+1))/(R+r));
>> normal=9.8*cos(aNormal)-(R+r)*w_c^2;
>> aNormal*180/pi
ans =   52.5008
>> normal
normal =   1.7764e-15

Al finalizar la segunda etapa, la posición del c.m. de la esfera es θ_n y su velocidad angular (dθ/dt)_n es

${\displaystyle {\left(\frac{d\theta }{dt}\right)}_n^2=\frac{g}{(R+r)}\left\{\begin{array}{l}\exp \left(2\mu ({\theta }_n-{\theta }_s)\right)\left(\frac{10}{7}-\frac{68{\mu }^2-4}{7(4{\mu }^2+1)}\cos {\theta }_s+\frac{6\mu }{4{\mu }^2+1}\sin {\theta }_s\right)\\ -\frac{6\mu }{4{\mu }^2+1}\text{sin}{\theta }_n+\frac{(4{\mu }^2-2)}{4{\mu }^2+1}\cos {\theta }_n\end{array}\right\}}$

Tiro parabólico

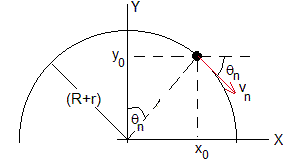
El c.m. de la esfera describe un movimiento parabólico, que parte de la posición x₀=(R+r)sinθ_n, y₀=(R+r)cosθ_n, con velocidad inicial v_n=(R+r)(dθ/dt)_n y haciendo un ángulo θ_n por debajo de la horizontal, tal como se aprecia en la figura. Las ecuaciones del movimiento son:

${\displaystyle \begin{array}{l}\overrightarrow{v}\{\begin{array}{l}{v}_x=v_n\cos {\theta }_n\\ v_y=-v_n\sin {\theta }_n-gt\end{array}\\ \overrightarrow{r}\{\begin{array}{l}x=R\sin {\theta }_n+v_n\cos {\theta }_{n}t\\ y=R\left(1-\cos {\theta }_n\right)-v_n\sin {\theta }_{n}t-\frac{1}{2}g{t}^2\end{array}\end{array}}$

Movimiento de rotación de la esfera

En la simulación más abajo, además del movimiento de traslación del centro de masas de la esfera, se visualiza el movimiento de rotación de la esfera alrededor de un eje que pasa por el cm.

Cuando la esfera rueda sin deslizar, en el intervalo de θ₀ a θ_s. El ángulo φ que gira la esfera está relacionado con la posición angular θ del centro de la esfera, (R+r)θ=rφ

El ángulo y la velocidad angular al finalizar la primera etapa, cuando θ=θ_s valen

${\displaystyle \begin{array}{l}{\phi }_s=\frac{\left(R+r\right)}{r}{\theta }_s\\ {\left(\frac{d\phi }{dt}\right)}_s=\frac{\left(R+r\right)}{r}{\left(\frac{d\theta }{dt}\right)}_s\end{array}}$

Estas son la posición angular y velocidad angular iniciales para la siguiente etapa del movimiento.

Cuando la esfera rueda y desliza, el movimiento de rotación y el movimiento de traslación no están relacionados. En esta etapa, entre los ángulos θ_s y θ_n, se resuelve por procedimientos numéricos el sistema de dos ecuaciones diferenciales

${\displaystyle \begin{array}{l}(R+r)\frac{d^2\theta }{d{t}^2}=g\sin \theta -\mu \left(g\cos \theta -(R+r){\left(\frac{d\theta }{dt}\right)}^2\right)\\ \frac{2}{5}r\frac{d^2\phi }{d{t}^2}=\mu \left(g\cos \theta -(R+r){\left(\frac{d\theta }{dt}\right)}^2\right)\end{array}}$

Con las condiciones iniciales especificadas: además de las mencionadas φ_s y (dφ/dt)_s, las que corresponden al movimiento del c.m. de la esfera: la posición inicial θ_s y su velocidad inicial (dθ/dt)_s, que describimos en apartados anteriores

Cuando la posición angular del centro de la esfera alcanza el ángulo crítico θ_n, la reacción N=0, la velocidad angular final de rotación de la esfera (dφ/dt)_n se mantien constante. El ángulo girado por la esfera desde ese instante es

${\displaystyle \phi ={\phi }_n+{\left(\frac{d\phi }{dt}\right)}_n\left(t-t_n\right)}$

Siendo t_n el instante en el que el centro de la esfera alcanza la posición θ_n y el ángulo girado por la esfera es φ_n

Actividades

Se introduce

• El radio r de la esfera en el control titulado Radio esfera
• El radio de la cúpula se ha fijado en R=1 m
• El coeficiente de rozamiento μ en el control titulado Coef. rozamiento que tendrá que ser mayor que cero
• El ángulo inicial de partida se ha fijado en θ₀=0.01 rad

Se pulsa el botón titulado Nuevo

Observamos el movimiento de traslación de la esfera sobre la cúpula y el movimiento de rotación alrededor de un eje que pasa por el c.m. Se señalan mediante líneas de color rojo y azul los ángulos críticos θ_s y θ_n.

Se calcula la energía (potencial gravitatoria, cinética de traslación y cinética de rotación) para cada etapa del movimiento, la energía se conserva excepto en la etapa en la que la esfera desliza, que disminuye ligeramente.

Se sugiere al lector probar con un rozamiento muy pequeño, pero no nulo. Para examinar el caso μ=0 se recomienda visitar la página titulada Movimiento sobre una cúpula semiesférica. Sin rozamiento

La esfera rueda sobre una cúpula semiesférica móvil

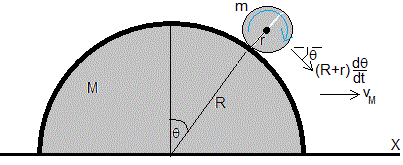
Supongamos que la cúpula semiesférica tiene masa M y se puede mover sin rozamiento en el plano horizontal. El análisis de este problema es similar al que se ha llevado a cabo en la página titulada Un cuerpo desliza sobre una cúpula semiesférica móvil.

Conservación del momento lineal

Sea M la masa de la cúpula y V_M su velocidad. La conservación del momento lineal a lo largo del eje X se escribe

${\displaystyle \begin{array}{l}M{V}_M+m\left((R+r)\frac{d\theta }{dt}\cos \theta +V_M\right)=0\\ V_M=-\frac{m\left(R+r\right)\frac{d\theta }{dt}\cos \theta }{m+M}\end{array}}$

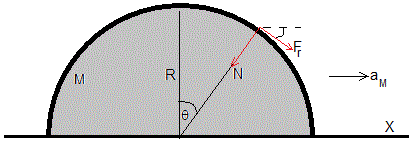
La velocidad de la cúpula, V_M es de sentido contrario al indicado en la figura, la cúpula se mueve hacia la izquierda

Conservación de la energía

${\displaystyle mg(R+r)-mg(R+r)\cos \theta =\frac{1}{2}M{V}_M^2+\frac{1}{2}m\left\{{\left((R+r)\frac{d\theta }{dt}\cos \theta +V_M\right)}^2+{\left((R+r)\frac{d\theta }{dt}\sin \theta \right)}^2\right\}+\frac{1}{2}\left(\frac{2}{5}m{r}^2\right){\left(\frac{d\phi }{dt}\right)}^2}$

Teniendo en cuenta que la esfera rueda sin deslizar

${\displaystyle \begin{array}{l}mg(R+r)\left(1-\cos \theta \right)=\frac{1}{2}M{V}_M^2+\frac{1}{2}m\left\{{\left(R+r\right)}^2{\left(\frac{d\theta }{dt}\right)}^2+2V_M\left(R+r\right)\frac{d\theta }{dt}\cos \theta +V_M^2\right\}+\frac{1}{5}m{\left((R+r)\frac{d\theta }{dt}\right)}^2\\ mg(R+r)\left(1-\cos \theta \right)=\frac{1}{2}\left(m+M\right)V_M^2+\frac{7}{10}m{\left(R+r\right)}^2{\left(\frac{d\theta }{dt}\right)}^2+m{V}_M\left(R+r\right)\frac{d\theta }{dt}\cos \theta \end{array}}$

En este sistema de dos ecuaciones, despejamos la velocidad de la cúpula V_M y la velocidad del centro de masas de la esfera (R+r)dθ/dt

${\displaystyle \begin{array}{l}{V}_M^2=\frac{10m^{2}g\left(R+r\right)\left(1-\cos \theta \right){\cos }^2\theta }{\left(7\left(M+m\right)-5m{\cos }^2\theta \right)\left(M+m\right)}\\ \left(R+r\right)\frac{d\theta }{dt}=-\frac{M+m}{m}\frac{V_M}{\cos \theta }\\ {\left(\frac{d\theta }{dt}\right)}^2=\frac{10g\left(M+m\right)\left(1-\cos \theta \right)}{\left(R+r\right)\left(7\left(M+m\right)-5m{\cos }^2\theta \right)}\end{array}}$

Ecuaciones del movimiento

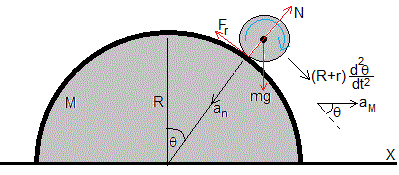
Supongamos que la aceleración de la cúpula semiesférica es a_M hacia la derecha. En la figura, se muestran las fuerzas sobre la esfera

• El peso, mg
• La reacción de la cúpula, N>0
• La fuerza de rozamiento, en el punto de contacto de la esfera con la cúpula, F_r

Para que la esfera ruede sin deslizar, F_r≤μN

• La ecuación del movimiento del c.m. de la esfera en la dirección tangencial

${\displaystyle m\left\{\left(R+r\right)\frac{d^2\theta }{d{t}^2}+a_M\cos \theta \right\}=mg\sin \theta -F_r}$

• La ecuación del movimiento del c.m. de la esfera en la dirección normal

${\displaystyle m\left\{\left(R+r\right){\left(\frac{d\theta }{dt}\right)}^2-a_M\sin \theta \right\}=mg\cos \theta -N}$

• La ecuación de la dinámica de rotación de la esfera

${\displaystyle \begin{array}{l}{F}_r·r=\left(\frac{2}{5}m{r}^2\right)\frac{d^2\phi }{d{t}^2}\\ F_r=\frac{2}{5}m\left(R+r\right)\frac{d^2\theta }{d{t}^2}\end{array}}$

• La ecuación del movimiento de la cúpula semiesférica a lo largo del eje X



${\displaystyle F_r\cos \theta -N\sin \theta =M{a}_M}$

En el sistema de cuatro ecuaciones eliminamos F_r y N, quedando el sistema de dos ecuaciones

${\displaystyle \begin{array}{l}\{\begin{array}{l}m\left\{\left(R+r\right)\frac{d^2\theta }{d{t}^2}+a_M\cos \theta \right\}=mg\sin \theta -\frac{2}{5}m\left(R+r\right)\frac{d^2\theta }{d{t}^2}\\ \frac{2}{5}m\left(R+r\right)\frac{d^2\theta }{d{t}^2}\cos \theta -\left\{mg\cos \theta -m\left(\left(R+r\right){\left(\frac{d\theta }{dt}\right)}^2+a_M\sin \theta \right)\right\}\sin \theta =M{a}_M\end{array}\\ \{\begin{array}{l}\frac{7}{5}\left(R+r\right)\frac{d^2\theta }{d{t}^2}+a_M\cos \theta =g\sin \theta \\ \frac{2}{5}m\left(R+r\right)\frac{d^2\theta }{d{t}^2}\cos \theta -mg\cos \theta \sin \theta +m\left(R+r\right){\left(\frac{d\theta }{dt}\right)}^2\sin \theta =\left(M+m{\sin }^2\theta \right)a_M\end{array}\end{array}}$

Despejamos la aceleración de la cúpula a_M

${\displaystyle \begin{array}{l}\frac{2}{7}m\left\{g\sin \theta -a_M\cos \theta \right\}\cos \theta -mg\cos \theta \sin \theta +m\left(R+r\right){\left(\frac{d\theta }{dt}\right)}^2\sin \theta =\left(M+m{\sin }^2\theta \right)a_M\\ -\frac{5}{7}mg\cos \theta \sin \theta +\frac{10g\left(M+m\right)\left(1-\cos \theta \right)}{7\left(M+m\right)-5m{\cos }^2\theta }\sin \theta =\left(M+m{\sin }^2\theta +\frac{2}{7}m{\cos }^2\theta \right)a_M\\ a_M=\frac{5mg\sin \theta \left(14\left(M+m\right)+5m{\cos }^3\theta -21\left(M+m\right)\cos \theta \right)}{{\left(7\left(M+m\right)-5m{\cos }^2\theta \right)}^2}\end{array}}$

La aceleración del centro de masas de la esfera es

${\displaystyle \left(R+r\right)\frac{d^2\theta }{d{t}^2}=\frac{5}{7}\left(g\sin \theta -a_M\cos \theta \right)}$

Angulos límite

• La reacción N=0 de la cúpula se hace cero.

La esfera deja de estar en contacto con la cúpula semiesférica, a_M=0

De la ecuación del movimiento en la dirección normal

${\displaystyle \left(R+r\right){\left(\frac{d\theta }{dt}\right)}^2=g\cos \theta }$

De la conservación de la energía y momento lineal

${\displaystyle \begin{array}{l}\frac{10g\left(M+m\right)\left(1-\cos \theta \right)}{7\left(M+m\right)-5m{\cos }^2\theta }=g\cos \theta \\ 5\frac{m}{M+m}{\cos }^3\theta -17\cos \theta +10=0\end{array}}$

El ángulo θ_n se obtiene resolviendo la ecuación cúbica en cosθ

Cuando la masa de la cúpula M o M+m es muy grande obtenemos el resultado anterior cosθ_n=10/17

• La esfera empieza a deslizar cuando F_r=μN

${\displaystyle \begin{array}{l}{F}_r=\mu N\\ \frac{2}{5}m\left(R+r\right)\frac{d^2\theta }{d{t}^2}=\mu \left\{mg\cos \theta -m\left(\left(R+r\right){\left(\frac{d\theta }{dt}\right)}^2-a_M\sin \theta \right)\right\}\\ \frac{2}{7}\left(g\sin \theta -a_M\cos \theta \right)=\mu g\cos \theta -\mu \frac{10g\left(M+m\right)\left(1-\cos \theta \right)}{\left(7\left(M+m\right)-5m{\cos }^2\theta \right)}+\mu a_M\sin \theta \\ \frac{2}{7}g\sin \theta -\mu g\cos \theta =\left(\frac{2}{7}\cos \theta +\mu \sin \theta \right)a_M-\mu \frac{10g\left(M+m\right)\left(1-\cos \theta \right)}{\left(7\left(M+m\right)-5m{\cos }^2\theta \right)}\end{array}}$

La raíz de la ecuación transcendente, nos da el ángulo θ_s para el cual la esfera empieza a deslizar

Cuando la masa de la cúpula M o M+m es muy grande, a_M≈0, obtenemos el resultado anterior (cúpula inmóvil)

${\displaystyle \begin{array}{l}\frac{2}{7}g\sin \theta -\mu g\cos \theta =-\mu \frac{10g\left(1-\cos \theta \right)}{7}\\ 2\sin \theta -17\mu \cos \theta +10\mu =0\end{array}}$

Referencias

Diego C. de Souza, Vitor R. Coluci. The motion of a ball moving down a circular path. Am. J. Phys. 85 (2) February 2017, pp. 124-129

Chinese Physics Olympiad 2018 Finals. Theoretical Exam. Solution. Problem 1. https://physoly.tech/static/files/archive/CPhO-2018-F-S.pdf