Movimiento de una esfera en una pista circular vertical
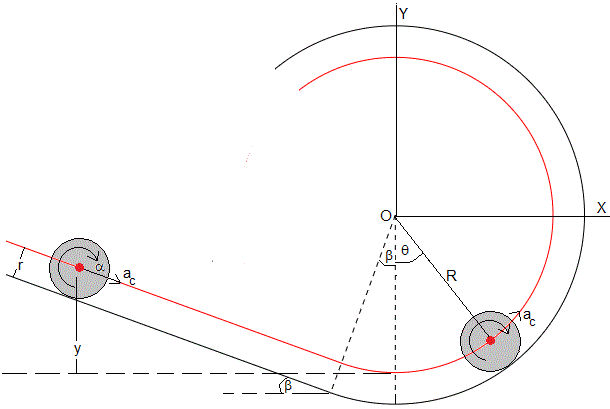
Como vemos en la figura, la pista consta de dos partes, una pista recta, inclinada un ángulo β, que enlaza con una pista circular de radio r+R. La parte recta de la pista es tangente a la circunferencia en el punto de coordenadas, -(r+R)sinβ, -(r+R)cosβ. La línea negra en la figura es la pista y la línea roja la trayectoria del centro (c.m.) de la esfera
Se suelta una esfera de radio r en la pista inclinada a una altura y=H. La esfera rueda sin deslizar a lo largo de la pista recta, entra en la pista circular en la posición angular -β y recorre la pista circular. La posición del centro de la esfera en la pista circular viene dada por el ángulo θ. Puede ocurrir que:
- La esfera ruede sin deslizar sobre la pista
- La esfera ruede y deslice
- Cuando la reacción de la pista se anule, N=0 , la esfera deja de tener contacto con la pista. El centro de la esfera describe una trayectoria parabólica hasta que impacta en el suelo.
La esfera rueda sobre la pista inclinada
A medida que la esfera rueda sin deslizar, disminuye la energía potencial del centro de la esfera. Como consecuencia, se incrementa la energía cinética de traslación del centro de masa (c.m.) de la esfera y la energía cinética de rotación alrededor de un eje que pasa por el c.m. El momento de inercia de la esfera de masa m y radio r es 2mr2/5.
Supongamos que la esfera se suelta a una altura H, la velocidad del centro de la esfera cuando se encuentra a una altura y se obtiene aplicando el principio de conservación de la energía. Si la esfera rueda sin deslizar, la velocidad angular de rotación alrededor de un eje que pasa por el centro de masa es vc/r. Siendo vc la velocidad de traslación del c. m.
La velocidad vc de la esfera al final del plano inclinado, se obtiene para, y=R-Rcosβ. Esta es la velocidad final de la esfera cuando abandona la pista inclinada y la inicial al entrar en la pista circular en la posición angular -β
Ecuaciones del movimiento
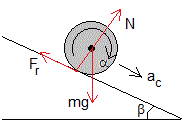
Cuando la esfera se mueve en el plano inclinado un ángulo β, las fuerzas que actúan son:
- El peso, mg
- La reacción N o fuerza que ejerce el plano inclinado sobre la esfera
- La fuerza de rozamiento Fr
En la figura, se representan las fuerzas sobre la esfera
-
Movimiento de traslación del centro de masa
Movimiento de rotación alrededor de un eje que pasa por el c.m
Si la esfera rueda sin deslizar, ambas aceleraciones están relacionadas, ac=rα.
mac=mgsinβ-Fr
Despejamos la fuerza de rozamiento Fr del sistema de ecuaciones y la aceleración del c.m.
La fuerza de rozamiento
El máximo valor de la fuerza de rozamiento es μsN=μsmgcosβ. Si Fr es menor que este valor, entonces la esfera rueda sin deslizar. Para un valor dado de μs el ángulo β del plano inclinado debe cumplir
En el programa interactivo, al final de esta página, el plano tiene 20° de inclinación, por lo que μs>0.104
Final de la primera etapa
La esfera se ha desplazado a lo largo del pista inclinada, x y la velocidad final de su c.m. es vc
Como rueda sin deslizar, habrá girado alrededor del eje que pasa por el c.m. un ángulo φ1=x/r
Movimiento en la pista circular: rueda sin deslizar
La posición angular del c.m. de la esfera en la pista viene dada por el ángulo θ, tal como vemos en la primera figura. La posición angular inicial de la esfera es θ=-β
La velocidad del centro de la esfera en la posición angular θ es
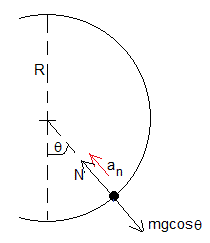
Como el c. m. de la esfera está describiendo un arco de circunferencia de radio R, por la dinámica del movimiento circular
La reacción N de la pista se hace cero y por tanto, la esfera cae, para el ángulo cos(θmax)=-10(H/R-1)/17, θmax sería el desplazamiento angular máximo de la esfera a lo largo de la pista
Para H/R=1, la esfera se detiene en la posición angular θ=π/2. Para H/R<1, la reacción N de la pista no puede ser cero, por lo que la partícula se detiene en la posición angular cosθ=(R-H)/R y regresa al punto de partida
Para que la esfera ruede sin deslizar, la fuerza de rozamiento Fr debe ser inferior al valor máximo μsN. Dado que N cambia con θ, la descripción del movimiento de la esfera en la pista circular vertical no es tan sencilla. Como veremos, la esfera rueda sin deslizar hasta un ángulo crítico θs y luego, desliza hasta que la reacción del plano se hace cero, θn y la esfera cae de la pista o bien, la esfera rueda sin deslizar hasta un ángulo crítico θs y luego, se detiene
Dependiendo del valor H/R y del coeficiente estático μs se pueden producir distintos casos que analizaremos con detalle a continuación
Ecuaciones del movimiento
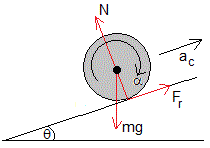
Cuando la esfera se mueve en la pista circular, las fuerzas que actúan son:
- El peso, mg
- La reacción N o fuerza que ejerce la pista sobre la esfera
- La fuerza de rozamiento Fr
En la figura, se representan las fuerzas sobre la esfera
-
Movimiento de traslación del centro de masa
Movimiento de rotación alrededor de un eje que pasa por el c.m
Si la esfera rueda sin deslizar, ambas aceleraciones están relacionadas, ac=rα.
mac=-mgsinθ+Fr
Despejamos la fuerza de rozamiento Fr del sistema de ecuaciones y la aceleración del c.m.
El centro de masas de la esfera describe un arco de circunferencia de radio R, la aceleración tangencial del c.m. ac es igual al radio R por la aceleración angular d2θ/dt2. Para calcular la posición angular θ del c.m. en función del tiempo t se precisa resolver, aplicando algún procedimiento numérico, la ecuación diferencial
con las condiciones iniciales siguientes: en el instante t=0, θ=-β, dθ/dt=vc/R, siendo vc la velocidad del c.m. al finalizar la primera etapa del movimiento
La fuerza de rozamiento
La esfera rueda sin deslizar, siempre que la fuerza de rozamiento Fr sea inferior al valor máximo μs·N.
Estudiamos la función
La función tiene una asíntota vertical, se hace infinito, cuando el denominador se hace cero, cuando 10(H/R-1)≤17, es decir, H/R≤2.7.
- Para H/R=2.7, la función tiende hacia infinito para el ángulo θ=π
- Para H/R<2.7, el denominador se hace cero para el ángulo
cos(θ)=-10(H/R-1)/17
Representamos la función f(θ) para varios valores del cociente H/R en el intervalo entre π/2 y π. De este modo, nos hacemos una idea del valor que tendría que tener μs para que la esfera describa la trayectoria circular vertical rodando sin deslizar.
hold on
for H_R=[2.7,2.75,2.8,2.9,3]
f=@(x) 2*sin(x)./(17*cos(x)+10*(H_R-1));
fplot(f,[pi/2,pi], 'displayName',num2str(H_R))
end
ylim([0,0.6])
set(gca,'XTick',pi/2:pi/6:pi)
set(gca,'XTickLabel',{'\pi/2','2\pi/3','5\pi/6','\pi'})
title('Coeficiente estático')
xlabel('\phi')
ylabel('\mu_s')
legend('-DynamicLegend','location','northwest')
grid on
hold off
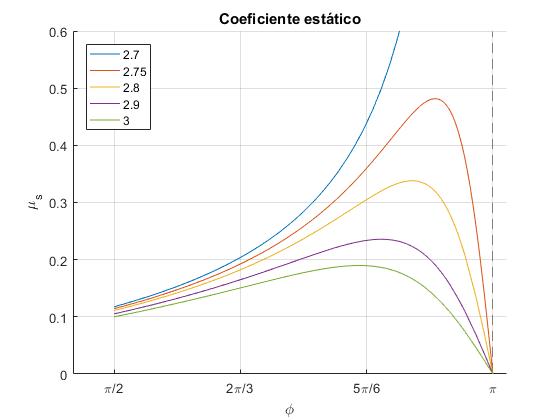
Cuando H/R>2.7, el valor mínimo de μs corresponde al máximo de la función f(θ).
Sustituyendo cosθmax en la función
Nos fijamos en la función f(θ) para H/R=2.75
>> acos(-17/(10*1.75)) ans = 2.9020 2/sqrt(100*1.75^2-289) ans = 0.4815
Así pues, μs tendrá que ser mayor que 0.4815, para que una esfera que se deja caer desde la altura H/R=2.75 ruede sin deslizar por la pista circular vertical.
Si μs es inferior al máximo, la ecuación
nos dará dos ángulos, el menor es la posición angular θs a partir de la cual la esfera desliza, tendremos que resolver esta ecuación transcendente por procedimientos numéricos
Mediante este script de MATLAB, dibujamos la función f(θ) para H/R=2.75, trazamos la recta μs=0.3, calculamos la raíz de la ecuación trascendente f(θ)=μs, que estará en el intervalo entre π/2 y θmax
R=1;
H=2.75;
mu_s=0.3; %coeficiente estático
%ángulo crítico para empezar a deslizar
f=@(x) 2*sin(x)./(17*cos(x)+10*(H/R-1));
hold on
fplot(f,[pi/2,pi])
set(gca,'XTick',pi/2:pi/6:pi)
set(gca,'XTickLabel',{'\pi/2','2\pi/3','5\pi/6','\pi'})
line([pi/2, pi],[mu_s,mu_s],'color','r')
th_max= acos(-17/(10*(H/R-1))); %máximo
line([th_max,th_max],[0,f(th_max)],'linestyle','--','color','k')
g=@(x) f(x)-mu_s;
aDesliza=fzero(g,[pi/2, th_max]); %primera raíz
line([aDesliza,aDesliza],[0,f(aDesliza)],'linestyle','--','color','b')
plot(aDesliza,0,'bo','markersize',4,'markeredgecolor','b',
'markerfacecolor','b')
hold off
ylim([0,0.6])
title('Angulo que empieza a deslizar')
xlabel('\phi')
ylabel('\mu_s')
grid on
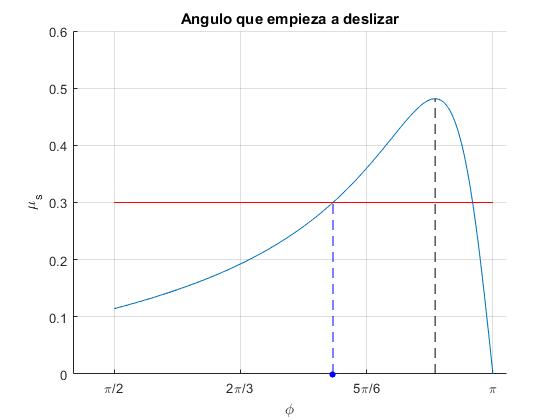
>> aDesliza*180/pi ans = 141.9935
Para H/R=2.75, la esfera empieza a deslizar en la posición angular 142°
Para H/R=2.7
>mu_s=0.3; >> aDesliza=2*atan(17*mu_s/2)*180/pi aDesliza = 137.1741
Para H/R=2.7, la esfera empieza a deslizar en la posición angular 137°
Para H/R<2.7
La función f(θ) tiene una asíntota vertical para el ángulo, cos(θmax)=-10(H/R-1)/17. Cualquiera que sea el coeficiente estático μs siempre habrá un ángulo θs<θmax, para el cual la esfera empieza a deslizar.
Mediante este script de MATLAB, dibujamos la función f(θ) para H/R=2.5, trazamos la recta μs=0.3, calculamos la raíz de la ecuación trascendente f(θ)=μs, que estará en el intervalo entre π/2 y θmax
R=1;
H=2.5;
mu_s=0.3;
f=@(x) 2*sin(x)./(17*cos(x)+10*(H/R-1));
hold on
fplot(f,[pi/2,pi], 'displayName',num2str(H))
set(gca,'XTick',pi/2:pi/6:pi)
set(gca,'XTickLabel',{'\pi/2','2\pi/3','5\pi/6','\pi'})
line([pi/2, pi],[mu_s,mu_s],'color','r')
g=@(x) f(x)-mu_s;
aDesliza=fzero(g,pi/2);
line([aDesliza,aDesliza],[0,f(aDesliza)],'linestyle','--','color','b')
plot(aDesliza,0,'bo','markersize',4,'markeredgecolor','b',
'markerfacecolor','b')
hold off
ylim([0,0.6])
title('Coeficiente estático')
xlabel('\phi')
ylabel('\mu_s')
grid on
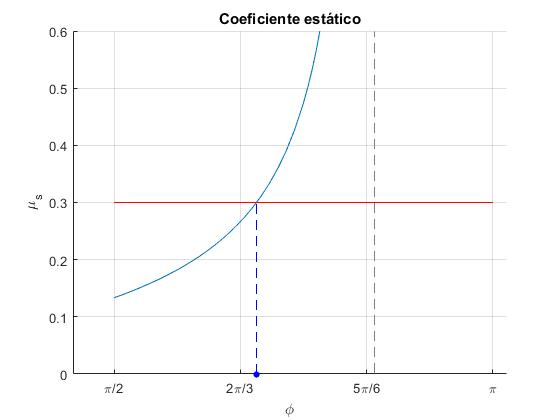
>> aDesliza*180/pi ans = 123.8169
Para H/R=2.5, la esfera empieza a deslizar en la posición angular 124°
Final de la segunda etapa
El final de la segunda etapa se produce:
Cuando H/R>2.7 y el coeficiente estático μs es mayor que el máximo de f(θ)
En caso contrario, cuando H/R≤2.7, o cuando H/R>2.7 y el coeficiente estático μs es menor que el máximo de f(θ)
La esfera rueda sin deslizar hasta alcanzar la posición final θ=π
la esfera empieza a deslizar para un ángulo θs<π
Aplicando el principio de conservación de la energía, la velocidad del c.m. de la esfera es
ya que la esfera rueda sin deslizar, el ángulo girado por la esfera al finalizar esta etapa será
Donde φ1 es el ángulo girado por la esfera en la primera etapa
Movimiento en la pista circular: desliza
Cuando un cuerpo desliza sobre un plano, la fuerza de rozamiento Fr=μk·N, donde N es la reacción del plano. El coeficiente cinético μk suele ser menor que el coeficiente estático μs
En este caso, los movimientos de traslación del c.m. y de rotación alrededor de un eje que pasa por el c.m. no están relacionados por vc=r·dφ/dt. La reacción N de la pista circular va disminuyendo y puede ocurrir, que se haga cero a cierto ángulo crítico θn<π, la esfera cae
Ecuaciones del movimiento
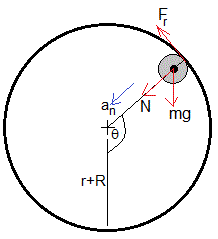
Cuando la esfera se mueve en la pista circular, las fuerzas que actúan son:
- El peso, mg
- La reacción N o fuerza que ejerce la pista sobre la esfera
- La fuerza de rozamiento Fr
En la figura, se representan las fuerzas sobre la esfera
-
Movimiento de traslación del centro de masa
Movimiento de rotación alrededor de un eje que pasa por el c.m
El centro de la esfera describe una arco de circunferencia de radio R con velocidad Rdθ/dt. Aplicamos la ecuación de la dinámica del movimiento circular
La reacción N de la pista circular
Eliminamos N entre la primera y la tercera ecuación, y procedemos de forma similar al estudio del movimiento de una partícula que desliza con rozamiento sobre un cúpula semicircular
Teniendo en cuenta que
Se transforma una ecuación diferencial de segundo orden en otra de primero.
con z=ω2. La solución de la ecuación diferencial se compone de dos términos:
La solución particular z1=Asinθ+Bcosθ
La solución de la ecuación diferencial homogénea
Introduciendo esta solución en la ecuación diferencial obtenemos los valores de los coeficientes A y B
Integrando ambos miembros obtenemos lnz=2μkθ+cte, o bien, z2=Cexp(2μkθ)
La solución completa es z=z1+z2
La constante C se determina a partir de las condiciones iniciales, para θ=θs, dθ/dt=(dθ/dt)s
La velocidad para la posición angular θs se calculó aplicando el principio de conservación de la energía vs=R(dθ/dt)s
Calculamos la constante C
La solución completa se expresa
Finalmente, la reacción N de la pista circular es
Calculamos el ángulo θn<π, para el que N se hace cero
Mediante este script de MATLAB, representamos N en función de θ para H/R=2.7 y μs=μk=0.3. Calculamos la posición angular θn<π que tendrá que ser mayor que θs para el que la reacción N se hace cero. En la primera parte del script, se calcula θs dado H/R y μs, en la segunda parte, se calcula θn dado θs y μk
R=1;
H=2.7; %es H/R, ya que R=1
mu_s=0.3; %coeficiente estático
%ángulo crítico para empezar a deslizar
f=@(x) 2*sin(x)./(17*cos(x)+10*(H/R-1))-mu_s;
aDesliza=pi;
if H>2.7
if mu_s<2/sqrt(100*(H7R-1)^2-289)
ang=acos(-17/(10*(H/R-1)));
aDesliza=fzero(f,[pi/2,ang]);
end
elseif H<2.7
aDesliza=fzero(f,pi/2);
else
aDesliza=2*atan(8.5*mu_s);
end
%la reacción N es nula
mu=mu_s;
g=@(x) 2*9.8*(5*(H-1+cos(aDesliza))/7-(3*mu*sin(aDesliza)+
(1-2*mu^2)*cos(aDesliza))/(4*mu^2+1))*exp(2*mu*(x-aDesliza))
+3*9.8*(2*mu*sin(x)+cos(x))/(4*mu^2+1);
hold on
fplot(g,[aDesliza,pi])
if sign(g(aDesliza))~=sign(g(pi))
aNormal=fzero(g,[aDesliza,pi]);
plot(aNormal,0,'ro','markersize',4,'markeredgecolor','r',
'markerfacecolor','r')
end
hold off
set(gca,'XTick',pi/2:pi/6:pi)
set(gca,'XTickLabel',{'\pi/2','2\pi/3','5\pi/6','\pi'})
grid on
xlabel('\theta')
ylabel('N');
title('Reacción de la pista')
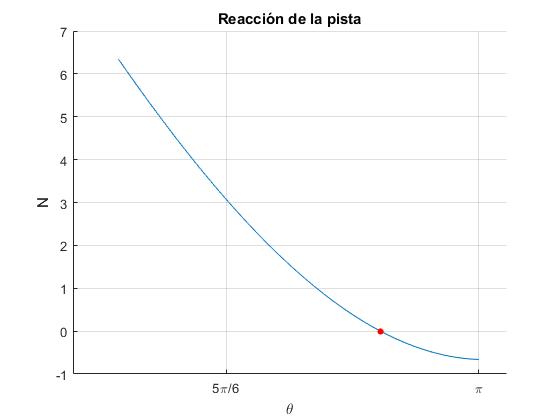
>> aNormal*180/pi ans = 168.3093
Para H/R=2.7 y μs=μk=0.3, la esfera cae en la posición angular θn=168°
Una partícula que parte de H/R=2.7 y que desliza sin rozamiento, alcanzaría la parte más alta de la trayectoria circular, θ=π. Sin embargo, una esfera que parte de la misma posición y que rueda sin deslizar, no la alcanza debido a que empieza a deslizar un poco antes de llegar dicha posición, perdiendo energía.
Las ecuaciones del movimiento
La ecuación del movimiento de traslación del c.m. es
La ecuación del movimiento de rotación alrededor de un eje que pasa por el c.m. es
Podríamos sustituir (dθ/dt)2, por la larga expresión en términos de θ deducida en el apartado anterior
Si solamente, estamos interesados en la posición del c.m. de la esfera, resolvemos la primera ecuación diferencial con las siguientes condiciones iniciales: en el instante t=0, θ=θs, con velocidad inicial (dθ/dt)s
Se estamos también interesados en el movimiento de rotación de la esfera, se resuelve el sistema de dos ecuaciones diferenciales con las condiciones adicionales, dφ/dt=R(dθ/dt)s/r y φ=φs.
Final de la tercera etapa
Si el movimiento transcurre en el primer cuadrante de la pista circular, θ<π/2, la reacción de la pista N no puede ser cero, la esfera rueda si deslizar, luego, empieza a deslizar para la posición angular θs hasta que finalmente, se detiene
Cuando la reacción N=0 de la pista circular se anula para la posición angular θn>π/2, la velocidad del c.m. de la esfera es vn=R(dθ/dt)n. La velocidad angular de rotación es (dφ/dt)n y el ángulo φn, en esta posición la esfera empieza a caer
Trayectoria parabólica
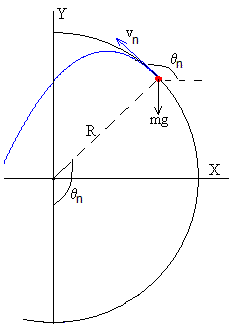
El c.m. de la esfera describe una trayectoria parabólica, que parte del punto (Rsinθn, R(1-cosθn)), con velocidad vn, haciendo un ángulo θn con la horizontal
La velocidad angular de rotación de la esfera se mantiene constante e igual a (dφ/dt)n. El ángulo girado φ al cabo de un cierto tiempo t es
Movimiento completo
En este apartado, describiremos el movimiento del c.m. de la esfera a lo largo de la pista circular cuya posición angular es θ.
El c.m. de la esfera parte de la posición angular -β con velocidad
Mientras la esfera está en contacto con la pista circular puede ocurrir, dependiendo de los valores de H/R y μs:
- Que la esfera ruede sin deslizar, en el intervalo entre -β y π
- Que la esfera ruede sin deslizar, en el intervalo entre -β y θs, y deslice en el intervalo θs a π
- Que la esfera ruede sin deslizar, en el intervalo entre -β y θs, deslice en el intervalo θs a θn, en ésta posición angular, la normal se hace cero
- Que la esfera ruede sin deslizar, en el intervalo entre -β y θs y deslice hasta que se detenga
- La esfera deja de estar en contacto con con pista circular en la posición angular θn y su c. m. describe una trayectoria parabólica
Completamos el script anterior resolviendo las ecuaciones diferenciales, por el procedimiento ode45 de MATLAB, que desciben el movimiento en la pista circular
Rueda sin deslizar
Rueda y desliza
con las condiciones iniciales siguientes: en el instante t=0, θ=-β, dθ/dt=vc/R, siendo vc la velocidad del c.m. al final de la pista inclinada
La velocidad del c.m. se puede calcular aplicando el principio de conservación de la energía
con las condiciones iniciales: en el instante t=0, θ=θs, velocidad inicial (dθ/dt)s
R=1;
H=0.7;
mu_s=0.3; %coeficiente estático
angulo=20*pi/180; %ángulo de la pista inclinada
%ángulo crítico para empezar a deslizar
f=@(x) 2*sin(x)./(17*cos(x)+10*(H/R-1))-mu_s;
aDesliza=pi;
if H>2.7
if mu_s<2/sqrt(100*(H/R-1)^2-289)
ang=acos(-17/(10*(H/R-1)));
aDesliza=fzero(f,[pi/2,ang]);
end
elseif H<2.7
aDesliza=fzero(f,[0,acos(-10*(H/R-1)/17)-0.1]);
%aDesliza=fzero(f,pi/2);
else
aDesliza=2*atan(8.5*mu_s);
end
%rueda sin deslizar
%velocidad en el punto más bajo de la pista circular
x0=[0,sqrt(10*9.8*(H/R-1+cos(angulo))/7)/R];
ff=@(t,x) [x(2);-9.8*5*sin(x(1))/(7*R)];
opts=odeset('events',@(t,x) stop_bucle_esfera(t,x,aDesliza));
[t,x]=ode45(ff,[0,100],x0,opts);
tFin=t(end);
hold on
plot(t,x(:,1)*180/pi)
%rueda y desliza
%La reacción N se hace cero para
if aDesliza<pi
mu=mu_s;
aNormal=pi; %ángulo límite para N=0
g=@(x) 2*9.8*(5*(H-1+cos(aDesliza))/7-(3*mu*sin(aDesliza)+
(1-2*mu^2)*cos(aDesliza))/(4*mu^2+1))*exp(2*mu*(x-aDesliza))
+3*9.8*(2*mu*sin(x)+cos(x))/(4*mu^2+1);
if sign(g(aDesliza))~=sign(g(pi))
aNormal=fzero(g,[aDesliza,pi]);
end
gg=@(t,x) [x(2); -9.8*sin(x(1))/R+mu*(9.8*cos(x(1))/R+x(2)^2)];
if aNormal>pi/2
opts=odeset('events',@(t,x) stop_bucle_esfera(t,x,aNormal));
else
opts=odeset('events',@(t,x) stop_bucle_esfera1(t,x));
end
%velocidad para el ángulo límite, empieza a deslizar
x0=[aDesliza,sqrt(10*9.8*(H/R-1+cos(aDesliza))/7)/R];
[t,x]=ode45(gg,[0,100],x0,opts);
plot(t+tFin,x(:,1)*180/pi)
line([0,tFin], [aDesliza,aDesliza]*180/pi, 'LineStyle','--','color','k')
line([tFin,tFin], [0,aDesliza]*180/pi, 'LineStyle','--','color','k')
if aNormal>pi/2
line([0,tFin+t(end)], [aNormal,aNormal]*180/pi, 'LineStyle','--',
'color','k')
line([tFin+t(end),tFin+t(end)], [0,aNormal]*180/pi, 'LineStyle',
'--','color','k')
else
line([0,tFin+t(end)], [x(end,1),x(end,1)]*180/pi, 'LineStyle','--',
'color','k')
line([tFin+t(end),tFin+t(end)], [0,x(end,1)]*180/pi, 'LineStyle',
'--','color','k')
end
end
hold off
grid on
xlabel('t')
ylabel('\theta');
title('Movimiento de la esfera')
El procedimiento de cálculo se detiene cuando la posición angular θ del c.m. alcanza el ángulo límite θs y θn, definiendo la función
function [value,isterminal,direction]=stop_cupula_esfera(~,x,xFin)
value=x(1)-xFin;
isterminal=1;
direction=0;
end
Si el ángulo final θ<π/2, la esfera rueda sin deslizar, desliza y se detiene. El procedimiento de cálculo se detiene cuando la velocidad final es cero, definiendo la función
function [value,isterminal,direction]=stop_bucle_esfera1(~,x)
value=x(2);
isterminal=1;
direction=0;
end
Cambiando los valores de las variables H (H/R) y mu_s (μs) en el script podemos explorar los casos mencionados:
Sea H/R=2.75 y μs=0.5, el coeficiente estático es mayor que el máximo de la función f(θ), por lo que la esfera rueda sin deslizar hasta que llega a la posición angular final θ=π
Sea H/R=2.75 y μs=0.3, el coeficiente estático es menor que el máximo de la función f(θ), por lo que la esfera rueda sin deslizar hasta la posición angular θs=142° y luego, desliza hasta que llega a la posición angular final θ=π
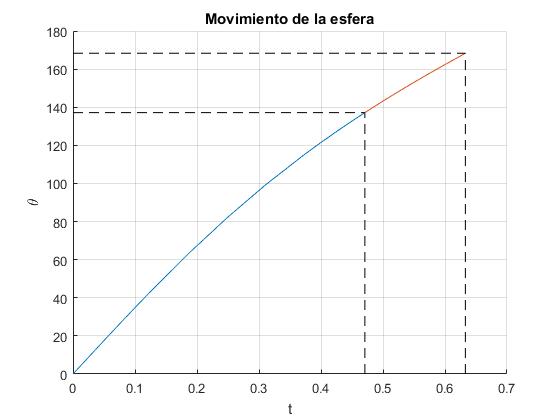
Sea H/R=2.7 y μs=0.3, la esfera desliza en la posición angular θs=137°, antes de llegar a la posición final θ=180°. La reacción N de la pista se hace cero en la posición angular θn=168° que es su posición final
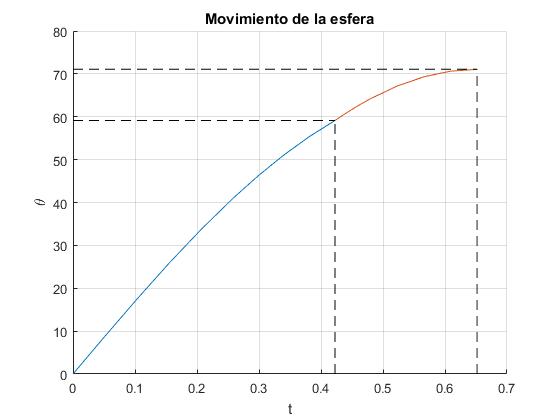
Sea H/R=0.7 y μs=0.3, si la esfera rodase sin deslizar, se detendría en la posición cos(θmax)=-10(H/R-1)/17, θmax=79.8°. La reacción de la pista no puede ser cero para θ<π/2. Por tanto, la esfera rueda sin deslizar hasta la posición angular θs=59° y luego, desliza hasta que se detiene en la posición final 71°
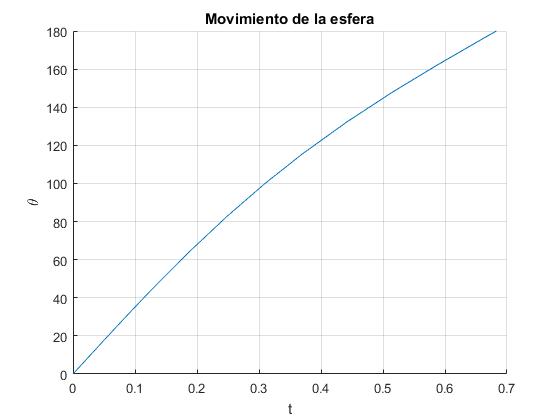
>> aDesliza*180/pi ans = 141.9935 >> aNormal*180/pi ans = 180
En color azul, se representa la primera etapa del movimiento: la esfera rueda sin deslizar. En color anaranjado, la segunda etapa: la esfera rueda y desliza, se señalan los instantes y los ángulos θs y θn
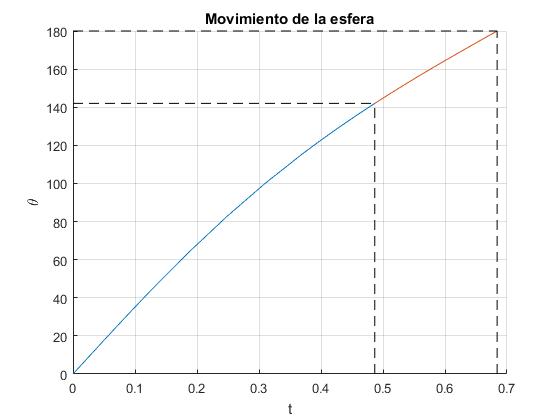
>> aDesliza*180/pi ans = 137.1741 >> aNormal*180/pi ans = 168.3093
>> acos(-10*(H/R-1)/17)*180/pi ans = 79.8358 >> aDesliza*180/pi ans = 59.1311 >> x(end,1)*180/pi ans = 71.0655
Actividades
Se introduce
- El radio de la esfera se ha fijado en r=0.2
- El radio del c.m. de la esfera se ha fijado en R=1 m
- El ángulo de la pista inclinada se ha fijado en β=20°
- El coeficiente estático μs en el control titulado Coeficiente estático que tendrá que ser mayor que 0.15
- La altura H/R a la que se suelta la esfera situada sobre la pista inclinada, en el control titulado Altura
Se pulsa el botón titulado Nuevo
Observamos el movimiento de la esfera sobre la pista. Se señalan mediante líneas de color azul, los ángulos críticos θs y θn.
Se calcula la energía (potencial gravitatoria, cinética de traslación y cinética de rotación) para cada etapa del movimiento, la energía se conserva excepto en la etapa en la que la esfera desliza, que disminuye ligeramente.
Referencias
Peter L. Tea, Jr. Trouble on the loop-the-loop, Am. J. Phys. 55 (9), September 1987, pp. 826-829

