Deformaciones de la rueda y del plano horizontal
Hasta ahora hemos supuesto que la rueda y el plano horizontal eran perfectamente rígidos, pero esta no es la situación real.
- Movimiento de un disco
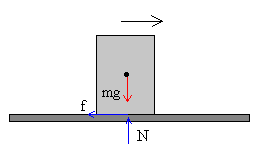
- Movimiento de un bloque
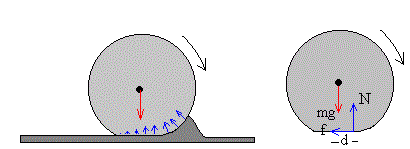
En la figura de la izquierda, vemos las fuerzas que se ejercen sobre un disco que se deforma y un plano horizontal que también se deforma. La resultante de las fuerzas que se ejercen en la superficie de contacto se muestran en la figura de la derecha.
Dicha resultante, tiene dos componentes: una componente vertical N y una componente horizontal f. La componente vertical N no pasa en general por el centro de masas, sino a una pequeña distancia d.
Las ecuaciones del movimiento para un disco de masa M y radio R son
La primera ecuación corresponde a la dinámica del movimiento de traslación del centro de masas. La segunda, la rotación alrededor de un eje que pasa por el c.m. La última ecuación, es la condición de rodar sin deslizar. El valor de la aceleración del c.m. ac y el valor de la fuerza f se pueden obtener de las ecuaciones del movimiento
La aceleración del cuerpo vale
Normalmente, el coeficiente dinámico μk es mucho mayor que el cociente d/R. Por lo que concluimos, que un cuerpo que desliza se detiene mucho antes que un cuerpo que rueda sin deslizar.
Movimiento uniforme
Calculamos la fuerza F que tenemos que aplicar en el c.m. para mantener ambos cuerpos (bloque y disco) en movimiento uniforme.
- En el caso del disco tenemos que ac=0 y α =0.
- En el caso del bloque obtenemos F=μkmg.
obtenemos que F=mgd/R.
De nuevo, concluimos que la fuerza F necesaria para mantener deslizando con velocidad constante a un cuerpo es superior a la fuerza necesaria para hacer rodar otro cuerpo de la misma masa, siempre que se cumpla que
Un cuerpo rígido que rueda sobre una superficie horizontal deformable.
En general, la deformación se produce en ambos cuerpos, en la mayor parte de los casos podemos suponer que es uno el que se deforma. Por ejemplo, en el caso del juego del billar, la bola experimenta una deformación mucho menor que el tapete. En el caso de un automóvil, la rueda experimenta mayor deformación que el asfalto o cemento de la carretera.
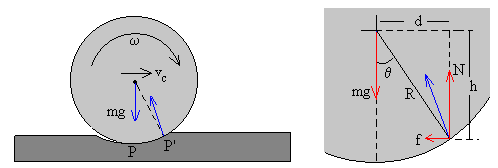
Consideremos el caso de una bola de billar que rueda sobre un tapete. Como se aprecia en la figura, la reacción es normal a la superficie en el punto de contacto y se aplica en un punto P’ que está muy cercano al punto P. La reacción no es vertical y tiene por tanto dos componentes N y f.
Observamos en la parte derecha de la figura, que d=Rsinθ. Para pequeñas deformaciones, el ángulo θ es pequeño, aproximamos sinθ≈θ y h≈R.
La componente f de la reacción se opone al movimiento de traslación del c.m. El momento resultante, f·h-N·d, favorece movimiento de rotación
Para una esfera I=2mR2/5, la aceleración ac del c.m.
Energías
La pérdida de energía se debe a la deformación de la superficie que está en contacto con el sólido que rueda y su vuelta a la forma inicial una vez que se ha desplazado, resultando una histéresis elástica que es la responsable de la pérdida de energía
La energía inicial es la suma de la energía cinética de traslación del centro de masa y de rotación alrededor de un eje que pas por el c.m.
Cuando el cuerpo se desplaza dx, el trabajo de las fuerzas que actúan sobre el cuerpo que rueda es
La fuerza f se opone al desplazamiento del cuerpo. El momento M=fR-Nd favorece el movimiento de rotación. Si el cuerpo rueda sin deslizar, dx=R·dθ
dW=-d·mg·dx/R
La fuerza f se opone al desplazamiento y a la vez, proporciona un momento que favorece la rotación, el trabajo neto de la fuerza f es nulo
Integrando, W=-d·mg·x/R
Cuando el cuerpo se detiene, la energía cinética inicial se convierte en trabajo
Ejemplo 1
- Radio de la rueda, R=4.96·10-3/2 m
- Masa, m=0.3973 kg
- Momento de inercia, I=6.57·10-4 kg·m2
- Aceleración, a=2.23·10-3 m/s2
- Velocidad inicial, v0=50.7·10-3 m/s
En la página titulada Medida de la velocidad y aceleración se explica como se mide la velocidad inicial y la aceleración de un cuerpo cuyo movimiento es rectilíneo y uniformemente acelerado, a partir de un registro de la posición xi en los instantes ti
De las ecuaciones del movimiento uniformente acelerado, obtenemos la distancia total recorrida por el cuerpo
xf=0.5763 m
Conocida la aceleración ac calculamos d=1.523·10-4 m
Conocido la distancia hasta que se detiene xf calculamos d=1.523·10-4 m
>> R=4.96e-3/2; >> m=0.3973; >> I=6.57e-4; >> a=2.23e-3; >> d=a*R*(1+I/(m*R^2)/9.8 d = 1.523e-04 >> v0=50.7e-3; >> xf=v0^2/(2*a); >> d=R*m*(1+I/m*R^2)*v0^2/(2*m*9.8*xf) d = 1.523e-04 d/R=0.0614
Ejemplo 2
En la misma pista, rueda un cuerpo hecho del mismo material pero con otras dimensiones
- Radio de la rueda, R=20·10-3/2 m
- Masa, m=0.7205 kg
- Momento de inercia, I=6.742·10-4 kg·m2
- Aceleración, a=32.6·10-3 m/s2
- Velocidad inicial, v0=192.7·10-3 m/s
>> R=20e-3/2; >> m=0.7205; >> I=6.742e-4; >> a=32.6e-3; >> d=a*R*(1+I/(m*R^2))/9.8 d = 3.4454e-04 >> v0=192.7e-3; >> xf=v0^2/(2*a); >> d=R*m*(1+I/(m*R^2))*v0^2/(2*m*9.8*xf) d = 3.4454e-04 >> d/R = 0.0345
Actividades
Se introduce
- El ángulo θ≈d/R en grados, en el control titulado Deformación
- La velocidad inicial del c.m. de la esfera se ha fijado en v0=1 m/s
Se pulsa el botón titulado Nuevo.
Se supone que la aproximación sinθ≈θ se mantiene hasta los 20º. En la parte inferior, observamos el movimiento de la bola de billar rodando sin deslizar sobre el plano horizontal. El programa interactivo nos proporciona la velocidad del c.m. en función del tiempo, y la distancia que recorre la bola de billar en dm. En la parte superior, vemos la deformación de la superficie horizontal y las fuerzas que actúan sobre la bola de billar.
Nota: un ángulo de 20º es bastante exagerado para la mayor parte de los casos prácticos, pero nos permite apreciar en la simulación la deformación de la superficie horizontal y las fuerzas que ejerce sobre la bola de billar.
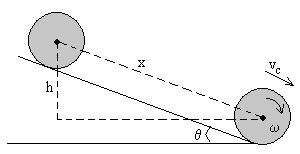
Un cuerpo rígido que se mueve sobre un plano inclinado deformable
El movimiento de un cilindro o una esfera a lo largo de un plano inclinado no se produce para cualquier inclinación del plano, por pequeña que esta sea, sino que requiere un ángulo umbral.
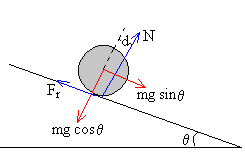
En la figura, se han dibujado las fuerzas que actúan sobre el cuerpo que rueda sin deslizar. Las componentes del peso, la fuerza de rozamiento en la rodadura Fr, la reacción N
La reacción N no se aplica en el punto de contacto entre la rueda y el plano, sino que pasa por delante del centro de masas a una distancia d del mismo. Su existencia se justifica como ya hemos visto en que el plano y la rueda se deforman ligeramente en la zona de contacto.
El valor del brazo d depende de diversos factores entre ellos la velocidad con que baja rodando el cuerpo, pero supondremos que es constante.
Como vemos en la figura, el momento de la reacción N=mgcosθ ya no es nulo sino que se opone al momento de la fuerza Fr.
Las ecuaciones del movimiento son ahora las siguientes:
- Movimiento de traslación del c.m.
- Movimiento de rotación alrededor de un eje que pasa por el c.m.
- La condición de que el cuerpo ruede sin deslizar es
mg·sinθ -Fr=mac
Fr·R-d·mgcosθ =Icα
ac=α ·R
Para un cilindro Ic=mR2/2
Que como vemos se convierten en las ecuaciones que describen el movimiento de un cilindro que rueda sin deslizar, cuando d=0.
El movimiento del cilindro no se inicia hasta un ángulo tal que ac≥ 0 es decir hasta que el ángulo θ>θ0
Relaciones energéticas
Al encontrarse el punto de contacto entre el cuerpo rígido y el plano inclinado instantáneamente en reposo sobre la superficie, la fuerza de rozamiento Fr es estática. El máximo valor que puede alcanzar es μs·N. Siendo N la reacción del plano inclinado N=mgcosθ . Mientras Fr no supere el valor máximo μs·mgcosθ , el movimiento del cuerpo será de rodar sin deslizar
La fuerza de rozamiento en la rodadura Fr no realiza trabajo neto. Pero ahora la reacción N si realiza un trabajo (momento por ángulo girado). –Nd·φ =-(d·mgcos θ )·x/R. Siendo x la longitud que recorre el cilindro a lo largo del plano inclinado.
De este modo, una parte de la energía potencial mgh se convierte en trabajo de la reacción N.
Si d=0 la energía potencial mgh se convierte en energía cinética de traslación del c.m. y en energía cinética de rotación alrededor de un eje que pasa por el c.m.
Ejemplo:
- Sea un cilindro de radio R=20 cm
- Supongamos que la reacción N del plano se aplica a una distancia d=1 cm del centro de masa.
El ángulo mínimo θ0 del plano inclinado para que el cilindro inicie el descenso es
tanθ0=1/20, θ0≈3º
-
Supongamos que el cilindro parte del reposo y recorre un plano de θ=3θº de inclinación y de x=3 m de longitud.
La aceleración del c.m. del cilindro es
La velocidad del c.m. en la base del plano inclinado es
Si x=3 m, vc=4.23 m/s
Aplicamos el balance energético
vc=4.23 m/s
Referencias
Hierrezuelo J., Carnero C.. Sliding and rolling: the physics of a rolling ball. Phys. Educ. 30 (1995), pp. 177- 182
López R., Gálvez F.J. Longitud de rodadura. Revista Española de Física 12 (1) 1998 págs. 41-43.
Surajit Chakrabarti, Rajesh B Khaparde, Alimohammed H Kachwala. Experimental study of the coefficient of rolling friction of the axle of a Maxwell's wheel on a soft horizontal surface. Eur. J. Phys. 41 (2020) 035803

