Movimiento en el plano horizontal

Sea una cinta de masa M, longitud L y espesor e pequeño comparado con el radio R de la cinta completamante enrollada.

En el instante t, el sistema consta de una cinta de longitud x, situada en el plano horizontal y un cilindro de masa m y radio r, cuyo centro C lleva una velocidad v que hace un ángulo θ con la horizontal y gira alrededor de un eje que pasa por C con velocidad angular ω. Supondremos que el cilindro rueda sin deslizar.

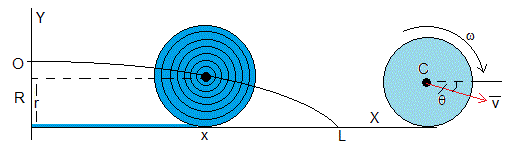
Como apreciamos en la figura, a medida que la cinta se desenrolla el radio r del cilindro disminuye, su centro C describe la trayectoria señalada en la figura que comienza en el origen O y termina en el punto (L,-R)

La longitud L de la cinta y su radio R cuando está completamente enrollada están relacionadas, πR²=Le.

El radio r del cilindro cuando se ha desenrollado una longitud x es, πr²=(L-x)e

${\displaystyle r=R\sqrt{1-\frac{x}{L}}=R\sqrt{1-u}}$

Siendo u=x/L, la proporción de cinta desenrollada

La masa del cilindro de radio r es, m=M(1-x/L)=M(1-u)

Principio de conservación de la energía

Aplicamos el principio de conservación de la energía a este sistema por que no hay un mecanismo aparente de disipación de la energía al menos durante las primeras etapas del movimiento. Al final, cuando se desenrolla completamente x tiende a L y la masa m tiende a cero. Un cilindro de masa m que tiende a cero y que lleva una energía finita, implica que la velocidad de su centro C tiende a infinito.

Energía potencial

Una parte de la cinta de masa (M-m) se encuentra en el plano horizontal, su energía potencial es -(M-m)gR. El centro de masas del cilindro de masa m se encuentra a una altura r, su energía potencial referida al origen O es -mg(R-r). La energía potencial total es E_p=-(M-m)gR-mg(R-r)

${\displaystyle E_p=-MgR\left(1-{\left(1-u\right)}^{3/2}\right)}$

Energía cinética

La parte x de la cinta desenrollada, se encuentra en reposo. La energía cinética del cilindro de masa m y radio r se compone de dos términos: la de traslación del centro de masas con velocidad v y la de rotación alrededor de un eje que pasa por el centro de masas con velocidad angular ω.

${\displaystyle E_k=\frac{1}{2}m{v}^2+\frac{1}{2}I{\omega }^2}$

Donde I=mr²/2 es el momento de inercia del cilindro

Las coordendas del centro C del cilindro son (x, -(R-r)). Derivando con respecto del tiempo obtenemos las componentes de la velocidad

${\displaystyle \begin{array}{l}{v}_x=\frac{dx}{dt}\\ v_y=\frac{dr}{dt}=-\frac{R}{2L}{\left(1-\frac{x}{L}\right)}^{-1/2}\frac{dx}{dt}\\ v^2={\left(\frac{dx}{dt}\right)}^2\left(\frac{R^2+4L^2(1-u)}{4L^2(1-u)}\right)\end{array}}$

La velocidad angular de rotación r·ω=dx/dt, de un sólido rígido de radio r que rueda sin deslizar. La energía cinética del cilindro, suma de los términos traslación y rotación, es

${\displaystyle E_k=\frac{1}{8}M\left(\frac{R^2+6L^2(1-u)}{L^2}\right){\left(\frac{dx}{dt}\right)}^2}$

Dado que la energía inicial es cero, el principio de conservación de la energía se escribe

${\displaystyle \frac{1}{8}M\left(\frac{R^2+6L^2(1-u)}{L^2}\right){\left(\frac{dx}{dt}\right)}^2-MgR\left(1-{\left(1-u\right)}^{3/2}\right)=0}$

Despejamos dx/dt y luego, calculamos el módulo de la velocidad v del centro C del cilindro

${\displaystyle \begin{array}{l}{\left(\frac{dx}{dt}\right)}^2=\frac{8gR{L}^2\left(1-{\left(1-u\right)}^{3/2}\right)}{R^2+6L^2(1-u)}\\ v^2=\frac{8gR{L}^2\left(1-{\left(1-u\right)}^{3/2}\right)}{R^2+6L^2(1-u)}\left(\frac{R^2+4L^2(1-u)}{4L^2(1-u)}\right)\end{array}}$

Cuando la cinta se desenrolla completamente, x tiende a L, o u tiende a 1, la velocidad v tiende a infinito.

Ecuación del movimiento

Le proporcionamos a la cinta completamente enrollada x=0, o u=0, una velocidad inicial (dx/dt)₀=V₀L , para que empiece a desenrollarse. La energía cinética inicial sería

${\displaystyle E_0=\frac{1}{8}M\left(R^2+6L^2\right)V_0^2}$

El principio de conservación de la energía se escribe en términos de u=x/L

${\displaystyle \frac{1}{8}M\left(R^2+6L^2\right)V_0^2=\frac{1}{8}M\left(R^2+6L^2(1-u)\right){\left(\frac{du}{dt}\right)}^2-MgR\left(1-{\left(1-u\right)}^{3/2}\right)}$

Despejamos du/dt

${\displaystyle {\left(\frac{du}{dt}\right)}^2=\frac{\left(R^2+6L^2\right)V_0^2+8gR\left(1-{\left(1-u\right)}^{3/2}\right)}{R^2+6L^2(1-u)}}$

Para obtener el tiempo t que tarda en desenrollarse x o la proporción u=x/L integramos con respecto de u.

${\displaystyle t={\displaystyle \underset{0}{\overset{u}{\int }}\sqrt{\frac{R^2+6L^2(1-u)}{\left(R^2+6L^2\right)V_0^2+8gR\left(1-{\left(1-u\right)}^{3/2}\right)}}}du}$

Para evitar la confusión entre el límite superior u y la variable u en el integrando, escribimos de forma equivalente.

${\displaystyle t={\displaystyle \underset{0}{\overset{u}{\int }}\sqrt{\frac{R^2+6L^2(1-z)}{\left(R^2+6L^2\right)V_0^2+8gR\left(1-{\left(1-z\right)}^{3/2}\right)}}}dz}$

Ejemplo

Sea la longitud de la cinta L=22.8 cm, el radio del cilindro cuando está completamente enrollada R=1.45 cm, la velocidad inicial v₀/L=V₀=0.36 s^-1

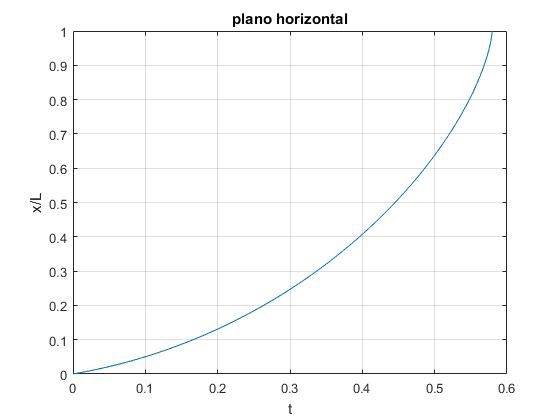
El tiempo T para que la cinta se desenrolle completamente, se obtiene poniendo el límite superior u=1 que equivale a x=L

>> R=1.45/100; %radio inicial
>> L=22.8/100; %longitud de la cinta
>> V0=0.36;  %velocidad incial (dx/dt)/L
 
>> f=@(x) sqrt((R^2+6*L^2*(1-x))./((R^2+6*L^2)*V0^2+8*9.8*R*(1-(1-x).^(3/2))));
>> integral(f,0,1)
ans =    0.5794

Elaboramos un script para representar la función implícita t=f(u), la posición u=x/L del centro del cilindro en función del tiempo t

R=1.45/100; %radio inicial
L=22.8/100; %longitud de la cinta
V0=0.36;  %velocidad incial (dx/dt)/L
 
f=@(x) sqrt((R^2+6*L^2*(1-x))./((R^2+6*L^2)*V0^2+8*9.8*R*(1-(1-x).^(3/2))));
uu=linspace(0,1,100);
t=zeros(1,length(uu));
i=1;
for u=uu
    t(i)=integral(f,0,u);
    i=i+1;
end
plot(t,uu)
grid on
xlabel('t')
ylabel('x/L')
title('plano horizontal')

Movimiento en el plano inclinado

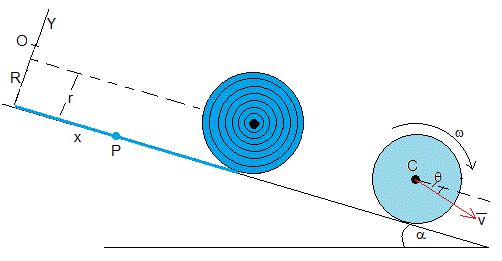
Estudiamos ahora el movimiento de la cinta en el plano inclinado. Establecemos los ejes como se indica en la figura, el eje X a lo largo del plano inclinado. La cinta parte del reposo, con energía cero. Lo único que cambia en esta situación es la energía potencial.

La energía potencial de la parte x de la cinta situada en el plano inclinado es -(M-m)g(xsinα/2+Rcosα). El centro de masa de esta parte de la cinta está en P distante x/2 del eje Y.

El centro C del cilindro de masa m y radio r, ha disminuido su altura en xsinα+(R-r)cosα, su energía potencial es mg(xsinα+(R-r)cosα)

${\displaystyle \begin{array}{l}{E}_p=-\left\{(M+m)g\frac{x}{2}\sin \alpha +(MgR-mgr)\cos \alpha \right\}=\\ -Mg\left\{(2-u)\frac{u}{2}L\sin \alpha +R\left(1-{\left(1-u\right)}^{3/2}\right)\cos \alpha \right\}\end{array}}$

La expresión de la energía cinética no cambia

${\displaystyle E_k=\frac{1}{8}M\left(\frac{R^2+6L^2(1-u)}{L^2}\right){\left(\frac{dx}{dt}\right)}^2=\frac{1}{8}M\left(R^2+6L^2(1-u)\right){\left(\frac{du}{dt}\right)}^2}$

Aplicamos el principio de conservación de la energía y despejamos du/dt

${\displaystyle {\left(\frac{du}{dt}\right)}^2=\frac{8g\left\{(2-u)\frac{u}{2}L\sin \alpha +R\left(1-{\left(1-u\right)}^{3/2}\right)\cos \alpha \right\}}{R^2+6L^2(1-u)}}$

Integramos respecto de u, para obtener la función implícita t=f(u), de la posición u=x/L en función del tiempo t

${\displaystyle t={\displaystyle \underset{0}{\overset{u}{\int }}\sqrt{\frac{R^2+6L^2(1-u)}{8g\left\{(2-u)\frac{u}{2}L\sin \alpha +R\left(1-{\left(1-u\right)}^{3/2}\right)\cos \alpha \right\}}}}du}$

Para evitar la confusión entre la variable u en el integrando y el límite superior u, escribimos de forma equivalente

${\displaystyle t={\displaystyle \underset{0}{\overset{u}{\int }}\sqrt{\frac{R^2+6L^2(1-z)}{8g\left\{(2-z)\frac{z}{2}L\sin \alpha +R\left(1-{\left(1-z\right)}^{3/2}\right)\cos \alpha \right\}}}}dz}$

Cuando la pendiente del plano inclinado se hace α=0, obtenemos la expresión de t=f(u) para el plano horizontal, deducida en el apartado anterior

El tiempo total que tarda en desenrollarse se obtiene cuando x=L, poniendo u=1 en el límite superior de la integral definida.

>> R=1.45/100; %radio inicial
>> L=22.8/100; %longitud de la cinta
>> alfa=pi/6;  %pendiente
 
>> f=@(x) sqrt((R^2+6*L^2*(1-x))./(8*9.8*((2-x).*x*L*sin(alfa)/2
+R*(1-(1-x).^(3/2))*cos(alfa))));
>> integral(f,0,1)
ans =    0.2918

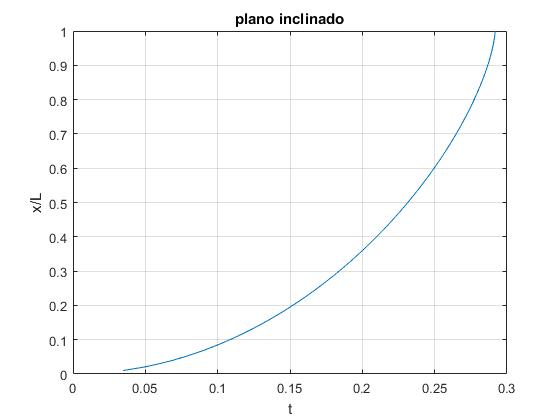
Elaboramos un script para representar la función implícita t=f(u), la posición u=x/L del centro del cilindro en función del tiempo t

R=1.45/100; %radio inicial
L=22.8/100; %longitud de la cinta
alfa=pi/6;  %pendiente
 
f=@(x) sqrt((R^2+6*L^2*(1-x))./(8*9.8*((2-x).*x*L*sin(alfa)/2+
R*(1-(1-x).^(3/2))*cos(alfa))));
uu=linspace(0.01,1,100);
t=zeros(1,length(uu));
i=1;
for u=uu
    t(i)=integral(f,0,u);
    i=i+1;
end
plot(t,uu)
grid on
xlabel('t')
ylabel('x/L')
title('plano inclinado')

Actividades

Se introduce

• La longitud L de la cinta, en el control titulado Longitud
• El ángulo del plano inclinado, en el control titulado Plano inclinado
• El espesor de la cinta se ha fijado en 0.25 cm

El programa interactivo calcula una tabla de tiempos t para valores de u comprendidos entre u=0.001 y u=1, con Δu=0.01, resolviendo la integral por procedimientos numéricos (fórmula de Simpson). El valor u=0 produce un error Infinity (infinito) como puede apreciarse en el integrando

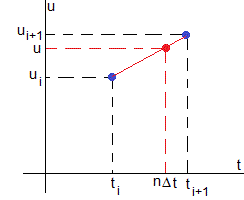
Para producir la animación, se calcula y se muestra las posiciones x=u·L del cilindro de radio variable para los tiempos n·Δt, donde n=1,2, ..... La posición correspondiente al instante n·Δt se calcula utilizando la interpolación lineal tal como se muestra en la figura

Una cinta se enrolla

En los apartados anteriores hemos estudiado cómo la cinta se desenrolla en el plano horizontal y en el plano inclinado. En este apartado, vamos a estudiar el caso contrario

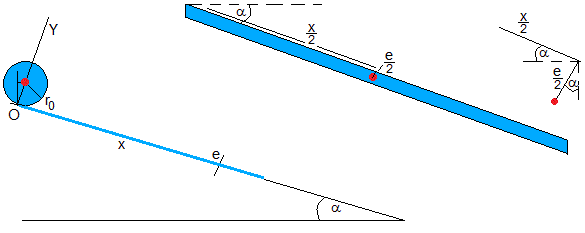
Supongamos una cinta enrollada de radio inicial r₀ y longitud l, se coloca en el origen O de un plano inclinado de ángulo α y se suelta, incrementando su radio r a medida que desciende

Conservación de la energía

La energía potencial de su centro de masas es

${\displaystyle V_0=m_{0}g{r}_0\cos \alpha =\rho \left(\pi r_0^{2}l\right)g{r}_0\cos \alpha }$

A la que hemos de sumar la energía potencial de la cinta (a la derecha en la figura) situada sobre el plano inclinado, de longitud x y espesor e. La energía potencial de su centro de masa es

${\displaystyle V_1=-\rho elxg\left(\frac{x}{2}\sin \alpha +\frac{e}{2}\cos \alpha \right)}$

Cuando la cinta enrollada se ha desplazado x, su masa m y radio r, son

${\displaystyle \begin{array}{l}m=\rho \left(\pi r^{2}l\right)=\rho \left(\pi r_0^{2}l\right)+\rho elx\\ \pi r^2=\pi r_0^2+ex\end{array}}$

Donde ρ es la densidad del material y l la longitud del cilindro de radio r

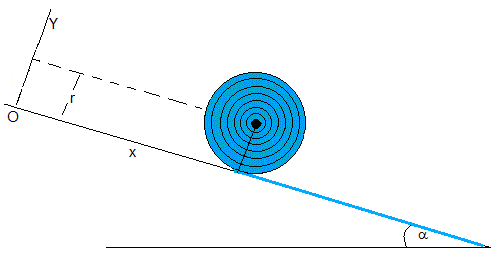
La energía potencial del centro de masa es

${\displaystyle V_2=-mgx\sin \alpha +mgr\cos \alpha }$

Las coordenadas del centro del cilindro son (x, r). La suma de energía cinética de traslación y de rotación alrededor del eje del cilindro es

${\displaystyle E_k=\frac{1}{2}m\left({\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dr}{dt}\right)}^2\right)+\frac{1}{2}\left(\frac{1}{2}m{r}^2\right){\omega }^2}$

La velocidad angular de rotación r·ω=dx/dt, de un sólido rígido de radio r que rueda sin deslizar.

El principio de conservación de la energía se escribe

${\displaystyle \begin{array}{l}\rho \left(\pi r_0^{2}l\right)g{r}_0\cos \alpha -\rho elxg\left(\frac{x}{2}\sin \alpha +\frac{e}{2}\cos \alpha \right)=\\ \frac{1}{2}\rho \left(\pi r^{2}l\right)\left({\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dr}{dt}\right)}^2\right)+\frac{1}{2}\left(\frac{1}{2}\rho \left(\pi r^{2}l\right)r^2\right)\frac{1}{r^2}{\left(\frac{dx}{dt}\right)}^2+\rho \left(\pi r^{2}l\right)g\left(-x\sin \alpha +r\cos \alpha \right)\end{array}}$

Teniendo en cuenta la relación entre r y x y su derivada

${\displaystyle 2\pi r\frac{dr}{dt}=e\frac{dx}{dt}}$

La conservación de la energía se escribe

${\displaystyle \frac{1}{4}\left(3\pi r^2+\frac{e^2}{2\pi }\right){\left(\frac{dx}{dt}\right)}^2=\pi r_0^{3}g\cos \alpha -\frac{g}{2}\left\{\left(2\pi r^3+e^{2}x\right)\cos \alpha +\left(e{x}^2-2\pi r^{2}x\right)\sin \alpha \right\}}$

Integramos para obtener la función implícita t=f(x)

${\displaystyle t={\displaystyle \underset{0}{\overset{x}{\int }}dz\sqrt{\frac{\frac{1}{4}\left(3\pi r^2+\frac{e^2}{2\pi }\right)}{\pi r_0^{3}g\cos \alpha -\frac{g}{2}\left\{\left(2\pi r^3+e^{2}z\right)\cos \alpha +\left(e·z^2-2\pi r^{2}z\right)\sin \alpha \right\}}}}}$

Las variables r y z en el integrando están relacionadas

${\displaystyle r^2=r_0^2+\frac{ez}{\pi }}$

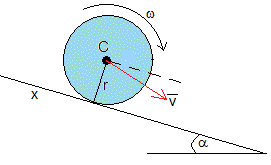
Elaboramos un script para representar la función implícita t=f(x), la posición x del centro del cilindro en función del tiempo t, con los siguientes datos

• Espesor de la cinta, e=5 mm
• Radio inicial de la cinta enrollada situada en el origen O, r₀=10 cm
• Angulo del plano inclinado, α=30°

function enrolla
    e=5/1000; %espesor, 5 mm
    r0=10/100; %radio inicial, 10 cm
    alfa=pi/6; %pendiente, 30°
    
    xx=linspace(0.01,1,100);
    t=zeros(1,length(xx));
    i=1;
    for x=xx
        t(i)=integral(@func,0,x);
         i=i+1;
    end
    plot(t,xx)
    grid on
    xlabel('t(s)')
    ylabel('x(m)')
    title('Posición')
  
    function res=func(z)
      r=sqrt(r0^2+e*z/pi);
      num=(3*pi*r.^2+e^2/(2*pi))/4;
      den=pi*r0^3*9.8*cos(alfa)-4.9*((2*pi*r.^3+e^2*z)*cos(alfa)+
(e*z.^2-2*pi*(r.^2).*z)*sin(alfa));
      res=sqrt(num./den);
    end
end

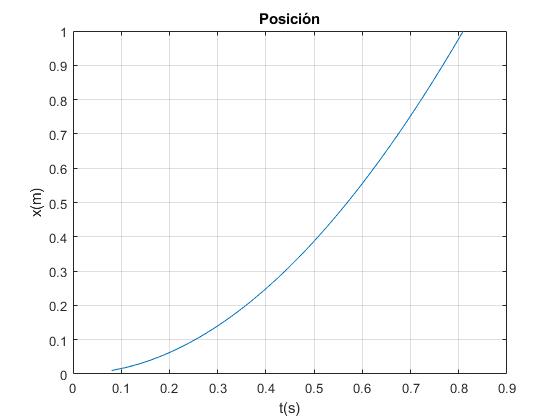
Representamos el radio r del cilindro en cm. Añadiendo al script

...
    r=sqrt(r0^2+e*xx/pi)*100; %radio en cm
    plot(t,r)
 ...

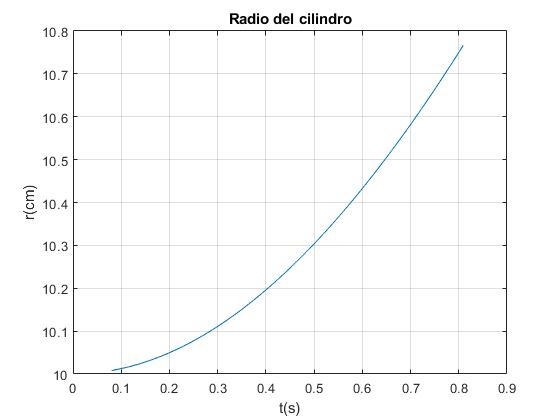
Representamos la componente a lo largo del plano inclinado de la velocidad v del cilindro. Añadiendo al primer script

...
     v=1./func(xx); %velocidad
     plot(t,v)
...

Derivamos con respecto del tiempo

${\displaystyle \left(1+\frac{e^2}{6{\pi }^2{r}^2}\right)\frac{dv}{dt}=\frac{2}{3}g\sin \alpha -g\frac{3re+e^2}{3\pi r^2}\cos \alpha -\frac{e}{2\pi r^2}{v}^2}$

Despreciando los términos en e²

${\displaystyle \frac{dv}{dt}\approx \frac{2}{3}g\sin \alpha -g\frac{e}{\pi r}\cos \alpha -\frac{e}{2\pi r^2}{v}^2}$

El primer término, corresponde a la aceleración del centro de masas de un cilindro que rueda sin deslizar a lo largo de un plano inclinado de ángulo α

Ecuaciones del movimiento

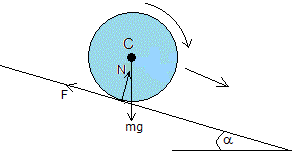
Las fuerzas sobre el cilindro de masa m y radio r son

• El peso, mg
• La reacción del plano inlinado, N
• La fuerza F en el punto de contacto

Escribimos la ecuación del movimiento de traslación del centro de masas, teniendo en cuenta que p_x es la componente del momento lineal a lo largo del plano inclinado y mgsinα-F es la resultante de las fuerzas a lo largo de dicha dirección

${\displaystyle \begin{array}{l}mg\sin \alpha -F=\frac{d{p}_x}{dt}\\ \left(\rho \pi r^{2}l\right)g\sin \alpha -F=m\frac{dv}{dt}+v\frac{dm}{dt}=\rho \pi r^{2}l\frac{dv}{dt}+v\frac{d\left(\rho \pi r^{2}l\right)}{dt}=\rho l\left(\pi r^2\frac{dv}{dt}+e{v}^2\right)\end{array}}$

La ecuación del movimiento de rotación alrededor del eje del cilindro

${\displaystyle rF=\frac{d(I_c\omega )}{dt}=\frac{d}{dt}\left(\frac{1}{2}m{r}^2\frac{v}{r}\right)=\frac{1}{2}\rho l\left(3\pi r^2\frac{dr}{dt}v+\pi r^3\frac{dv}{dt}\right)=\frac{1}{2}\rho l\left(\frac{3}{2}er{v}^2+\pi r^3\frac{dv}{dt}\right)}$

Eliminamos la fuerza desconocida F en el sistema de dos ecuaciones

${\displaystyle \frac{dv}{dt}=\frac{2}{3}g\sin \alpha -\frac{7}{6}\frac{e}{\pi r^2}{v}^2}$

Esta ecuación no coincide con la obtenida a partir de la conservación de la energía.

Referencias

Ira M. Freeman. The Dynamics of a Roll of Tape. Am. J. Phys. 14 (1946) pp. 124-126

Carl E Mungan, Trevor C Lipscombe, When experiment and energy conservation collide: video analysis of an unrolling mat. Eur. J. Phys. 39 (2018) 025004

Kirk T. McDonald. Snowball/Log Rolling down a Snowy Slope. May 25,2019. https://www.physics.princeton.edu/~mcdonald/examples/snowball.pdf