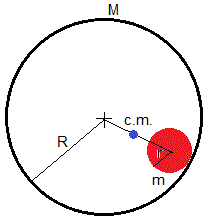
Consideremos un cilindro hueco de masa M y radio R de pequeño espesor, (en color negro) al que se ha soldado un cilindro macizo de masa m y radio r (de color rojo), tal como se muestra en la figura. La distancia r_cmdel centro de masas al centro del cilindro hueco es

${\displaystyle r_{cm}=\frac{m}{m+M}(R-r)}$

El momento de inercia I_cm del sistema respecto de un eje paralelo al del cilindro que pasa por el centro de masa es

${\displaystyle \begin{array}{l}{I}_{cm}=M{R}^2+M{r}_{cm}^2+\frac{1}{2}m{r}^2+m{\left((R-r)-r_{cm}\right)}^2=\\ M{R}^2+\frac{1}{2}m{r}^2+\frac{mM}{m+M}{\left(R-r\right)}^2\end{array}}$

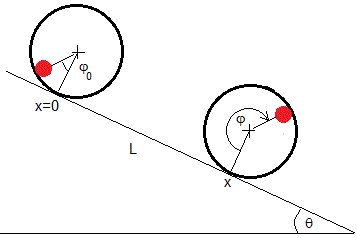
El cilindro hueco parte del origen de un plano inclinado de longitud L y ángulo θ. El cilindro macizo forma un ángulo inicial φ₀. Cuando el centro del cilindro hueco se desplaza x a lo largo del plano inclinado, el ángulo que gira el cilindro macizo es φ-φ₀. De modo que, x=R(φ-φ₀), tal como se muestra en la figura

Energía cinética

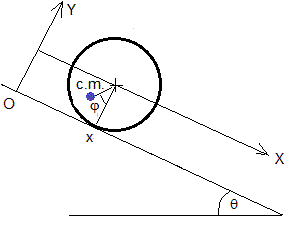
El movimiento del cilindro asimétrico es la suma de dos movimientos: de la traslación del centro de masas y el movimiento de rotación alrededor de un eje paralelo al de los cilindros y que pasa por el centro de masas

La posición del centro de masas es

${\displaystyle \{\begin{array}{l}{x}_{cm}=x-r_{cm}\sin \phi =R(\phi -{\phi }_0)-r_{cm}\sin \phi \\ y_{cm}=-r_{cm}\cos \phi \end{array}}$

Derivando respecto del tiempo, obtenemos la velocidad del centro de masas

${\displaystyle \{\begin{array}{l}\frac{d{x}_{cm}}{dt}=R\frac{d\phi }{dt}-r_{cm}\cos \phi \frac{d\phi }{dt}\\ \frac{d{y}_{cm}}{dt}=r_{cm}\sin \phi \frac{d\phi }{dt}\end{array}}$

La energía cinética del cilindro es la suma de la energía cinética de traslación del centro de masas y la energía cinética de rotación, con velocidad angular dφ/dt, alrededor de un eje paralelo a los ejes de los cilindros que pasa por el centro de masas

${\displaystyle \begin{array}{l}{E}_k=\frac{1}{2}\left(M+m\right)\left({\left(\frac{d{x}_{cm}}{dt}\right)}^2+{\left(\frac{d{y}_{cm}}{dt}\right)}^2\right)+\frac{1}{2}{I}_{cm}{\left(\frac{d\phi }{dt}\right)}^2=\\ =\frac{1}{2}\left((2M+m)R^2+\frac{1}{2}m{r}^2+m{(R-r)}^2-2mR(R-r)\cos \phi \right){\left(\frac{d\phi }{dt}\right)}^2=\\ =\frac{1}{2}\left(I-2mR(R-r)\cos \phi \right){\left(\frac{d\phi }{dt}\right)}^2\end{array}}$

Donde la variable I agrupa los términos constantes

${\displaystyle I=(2M+m)R^2+\frac{1}{2}m{r}^2+m{(R-r)}^2}$

Energía potencial

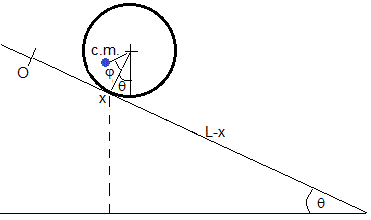
En un momento dado, el cilindro se encuntra en la posición x. Tomando el nivel cero de energía potencial en el vértice del plano inclinado de longitud L, la energía potencial del centro de masas es

${\displaystyle \begin{array}{l}{E}_p=(M+m)g{h}_{cm}=(M+m)g\left((L-x)\sin \theta +R\cos \theta -r_{cm}\cos (\theta +\phi )\right)=\\ (M+m)gL\sin \theta +(M+m)gR\cos \theta -(M+m)gR(\phi -{\phi }_0)\sin \theta -mg(R-r)\cos (\theta +\phi )\end{array}}$

Los dos primeros términos son constantes y no intervienen en la ecuación del movimiento

Ecuación del movimiento

La Lagrangiana es la diferencia E_k-E_p

${\displaystyle \begin{array}{l}L=\frac{1}{2}\left(I-2mR(R-r)\cos \phi \right){\left(\frac{d\phi }{dt}\right)}^2+(M+m)gR(\phi -{\phi }_0)\sin \theta \\ +mg(R-r)\cos (\theta +\phi )\end{array}}$

La ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\phi }}\right)-\frac{\partial L}{\partial \phi }=0\\ \left(I-2mR(R-r)\cos \phi \right)\frac{d^2\phi }{d{t}^2}+mR(R-r)\sin \phi {\left(\frac{d\phi }{dt}\right)}^2-(M+m)gR\sin \theta +\\ mg(R-r)\sin (\theta +\phi )=0\end{array}}$

Se resuelve la ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, el cilindro macizo se ha desplazado φ₀ y el sistema parte del reposo. La posición x del cilindro hueco es x=R(φ-φ₀)

Ejemplo

Consideremos el siguiente sistema:

• Masa del cilindro hueco, M=200 g
• Radio del cilindro hueco, R=10 cm
• Masa del cilindro macizo, m=800 g
• Radio del cilindro macizo, r=1.2 cm
• Angulo del plano inclinado, θ=10°

Sea el desplazamiento inicial del cilindro macizo φ₀=120°, señalado por un punto de color rojo en la figura más abajo

Representamos la función energía potencial E_p(φ) y la energía inicial E₀=E_p(φ₀) mediante una recta horizontal

M=0.2; % cilindro hueco
R=0.1; %cilindro hueco
m=0.8; %cilindro macizo
r=0.012; %radio macizo
theta=10*pi/180; %plano inclinado
 
fi_0=120*pi/180; %ángulo inicial
%energía potencial
Ep=@(x) (M+m)*sin(theta)+(M+m)*R*cos(theta)-(M+m)*R*(x-fi_0)*sin(theta)
-m*(R-r)*cos(theta+x);
E0=Ep(fi_0); %energía inicial
hold on
fplot(Ep,[-pi,5*pi])
line([-pi,5*pi],[E0,E0])
plot(fi_0,E0, 'ro', 'markersize',4,'markerfacecolor','r')
%mínimo y máximo
fi=asin((M+m)*R*sin(theta)/(m*(R-r)))-theta; %mínimo
plot(fi,Ep(fi), 'bo', 'markersize',4,'markerfacecolor','b')
fi=pi-asin((M+m)*R*sin(theta)/(m*(R-r)))-theta; %máximo
plot(fi,Ep(fi), 'bo', 'markersize',4,'markerfacecolor','b')

hold off
xlabel('\phi')
ylabel('E_p');
title('Energía potencial')
grid on

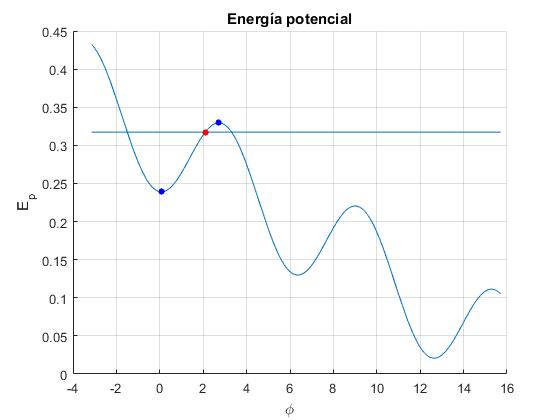
El sistema oscila entre dos posiciones, una de ellas es x=R·φ₀ y la otra se obtiene resolviendo la ecuación transcendente E₀=E_p(φ)

>> f=@(x) Ep(x)-E0;
>> fzero(f,-120*pi/180)
ans =   -1.4992

que son -85.9°

Calculamos el máximo y mínimo local de la función energía potencial, representados por los puntos de color azul

${\displaystyle \frac{d{E}_p(\phi )}{d\phi }=-(M+m)gR\sin \theta +mg(R-r)\sin (\theta +\phi )=0}$

El primer mínimo corresponde al ángulo ø

${\displaystyle \theta +\varphi =\arcsin \left(\frac{(M+m)R}{m(R-r)}\sin \theta \right)}$

El primer máximo ø se obtiene para

${\displaystyle \theta +\varphi =\pi -\arcsin \left(\frac{(M+m)R}{m(R-r)}\sin \theta \right)}$

Con los datos del ejemplo, el máximo local se obtiene para ø=155.7°

Para ángulos iniciales φ₀<ø el movimiento es oscilatorio y para ángulos mayores el cilindro baja rodando por la rampa. Esta posición es de equilibrio inestable y corresponde a la frontera entre dos tipos completamente diferentes de movimiento

Resolvemos la ecuación diferencial del movimiento para obtener la velocidad del centro del cilindro en función del tiempo.

M=0.2; % masa cilindro hueco
R=0.1; % radio cilindro hueco
m=0.8; % masa cilindro macizo
r=0.012; %radio cilindro macizo
theta=10*pi/180; %plano inclinado
fi_0=120*pi/180; %ángulo inicial

I=(2*M+m)*R^2+m*r^2/2+m*(R-r)^2; 
 
f=@(t,x) [x(2);((M+m)*9.8*R*sin(theta)-m*9.8*(R-r)*sin(theta+x(1))-
m*R*(R-r)*sin(x(1))*x(2)^2)/(I-2*m*R*(R-r)*cos(x(1)))]; 
[t,x]=ode45(f,[0,4],[fi_0,0]);
plot(t,R*x(:,2))
xlabel('t')
ylabel('v');
title('Movimiento oscilatorio')
grid on

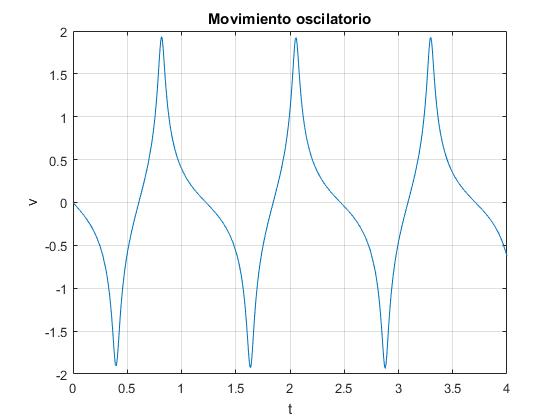
Se podría medir el periodo o la diferencia de tiempos entre dos máximos o dos mínimos

Si cambiamos el ángulo inicial a φ₀=180° el sistema baja rodando por el plano inclinado

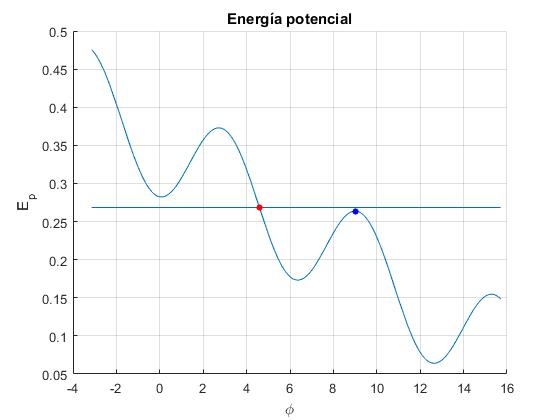
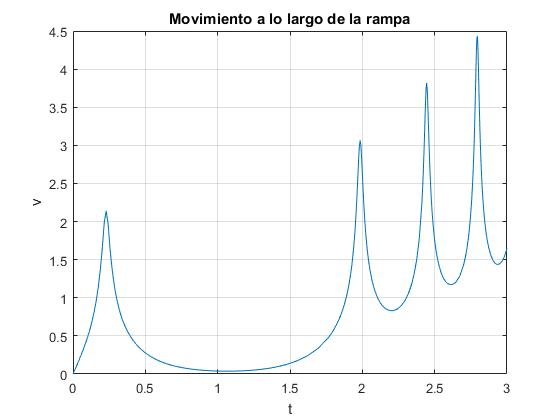
Para φ₀=263°, la energía inicial (punto de color rojo) es próxima a un máximo local (punto de color azul), el cilindro rueda a lo largo de la rampa, pero casi se detiene

M=0.2; % cilindro hueco
R=0.1; %cilindro hueco
m=0.8; %cilindro macizo
r=0.012; %radio macizo
theta=10*pi/180; %plano inclinado
 
fi_0=263*pi/180; %ángulo inicial
%energía potencial
Ep=@(x) (M+m)*sin(theta)+(M+m)*R*cos(theta)-
(M+m)*R*(x-fi_0)*sin(theta)-m*(R-r)*cos(theta+x);
E0=Ep(fi_0); %energía inicial
hold on
fplot(Ep,[-pi,5*pi])
line([-pi,5*pi],[E0,E0])
plot(fi_0,E0, 'ro', 'markersize',4,'markerfacecolor','r')
fi=pi-asin((M+m)*R*sin(theta)/(m*(R-r)))-theta; %máximo
plot(fi+2*pi,Ep(fi+2*pi), 'bo', 'markersize',4,'markerfacecolor','b')

hold off
xlabel('\phi')
ylabel('E_p');
title('Energía potencial')
grid on

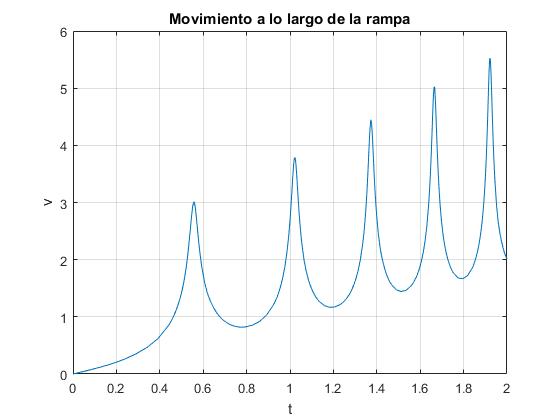
Resolvemos la ecuación diferencial del movimiento

Actividades

Introducimos

• La masa del cilindro hueco, M, en el control titulado Masa cilindro hueco
• La masa del cilindro macizo, m, en el control titulado macizo
• El radio del cilindro hueco, R se ha fijado en 10 cm
• El radio del cilindro macizo, r, en el control titulado Radio
• El ánngulo inicial φ₀, en el control titulado Angulo inicial
• El ángulo del plano inclinado, θ, en el control titulado Plano inclinado

Se pulsa el botón titulado Nuevo

Observamos el movimiento del sistema formado por el cilindro hueco (en color negro) y del cilindro macizo (en color rojo) rodando a lo largo del plano inclinado. A la derecha, se representa la velocidad del centro del cilindro en función del tiempo

Referencias

Antonino Carnevali. Russel May. Rolling motion of non-axisymmetric cylinders. Am J. Phys. 73 (10) October 2005, pp. 909-913