Superficie cilíndrica cóncava

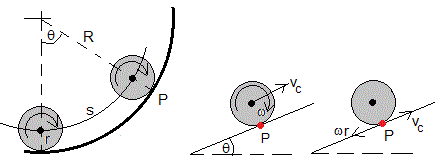
Como hemos demostrado, para que un cuerpo en forma de aro, cilindro o esfera de radio r, ruede sin deslizar en un plano horizontal o inclinado, se tiene que cumplir que v_c=ωr, a fin de que la velocidad del punto P de contacto del cuerpo con el plano sea nula. Donde

• v_c es la velocidad del centro de masas
• ω es la velocidad angular de rotación alrededor de un eje que pasa por el centro

En el caso de que el cuerpo ruede sobre una superficie cilíndrica, la velocidad del centro de masas es

${\displaystyle v_c=\frac{ds}{dt}=(R-r)\frac{d\theta }{dt}}$

La velocidad angular de rotación es

${\displaystyle \omega =\frac{d\phi }{dt}}$

Para que la velocidad del punto P de contacto sea nula, se tiene que cumplir que

${\displaystyle (R-r)\frac{d\theta }{dt}=r\frac{d\phi }{dt}}$

La relación entre el desplazamiento angular del centro del cuerpo θ y el ángulo φ girado por el cuerpo es (R-r)θ=rφ

Vamos a comprobar esta relación de forma geométrica

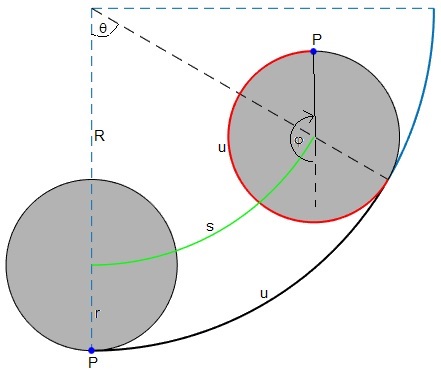
Un cuerpo de radio r rueda sin deslizar sobre una superficie cilíndrica de radio R. El centro del cuerpo describe un arco s=(R-r)θ (en color verde), mientras el cuerpo rueda una longitud u=Rθ sobre la pista (en color negro) e igual al arco de color rojo pintado sobre el cuerpo.

En la figura, se señala la posición inicial del punto P del cuerpo y su posición angular en el instante t, φ=u/r-θ=Rθ/r-θ o bien, (R-r)θ=rφ

${\displaystyle \phi =\frac{R-r}{r}\theta }$

Parte de la figura ha sido elaborada con el siguiente código

th=pi/3; %ángulo
r=0.25; %radio del cuerpo que rueda
hold on
%pista
fplot(@(t) cos(t), @(t) sin(t), [-pi/2,0], 'linewidth',1.5)
%cuerpo
ang=(1:360)*pi/180;
x1=r*cos(ang);
y1=-(1-r)+r*sin(ang);
fill(x1,y1,[0.7 0.7 0.7])
line([0,0],[0,-1],'linestyle','--')
line([0,1],[0,0],'linestyle','--')

x1=(1-r)*sin(th)+r*cos(ang);
y1=-(1-r)*cos(th)+r*sin(ang);
fill(x1,y1,[0.7 0.7 0.7])
line([0,sin(th)],[0,-cos(th)],'linestyle','--','color','k')
fplot(@(t) cos(t), @(t) sin(t), [-pi/2,-(pi/2-th)], 'linewidth',
1.5,'color','k')
fplot(@(t) (1-r)*sin(th)+r*cos(t), @(t) -(1-r)*cos(th)+r*sin(t), 
[-th/r-(pi/2-th),-(pi/2-th)], 'linewidth',1.5, 'color','r')
fplot(@(t) (1-r)*cos(t), @(t) (1-r)*sin(t), [-pi/2,-(pi/2-th)], 
'linewidth',1,'color','g')
plot(0,-1,'bo','linewidth',1,'markersize',4,'markeredgecolor','b',
'markerfacecolor','b')
plot((1-r)*sin(th)+r*cos(-th/r-(pi/2-th)),-(1-r)*cos(th)+
r*sin(-th/r-(pi/2-th)),'bo','linewidth',1,'markersize',4,'markeredgecolor',
'b','markerfacecolor','b')

hold off
axis equal
axis off

Ecuaciones del movimiento

Cuando el cuerpo asciende disminuye su velocidad v_c y ω

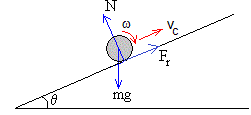
Las fuerzas sobre el cuerpo:

• El peso mg
• La reacción N de la superficie cilíndrica en el punto de contacto P
• La fuerza de rozamiento F_r, cuyo momento hace que disminuya la velocidad angular ω

Formulamos las ecuaciones del movimiento:

• Movimiento de traslación del centro de masas con aceleración a_c=d²s/dt²

${\displaystyle -mg\sin \theta +F_r=m\frac{d^{2}s}{d{t}^2}}$

• Movimiento de rotación alrededor de un eje que pasa por el centro de masas con aceleración angular α=d²φ/dt²

Para un cuerpo redondo (aro, cilindro o esfera) de masa m y de radio r y cuyo momento de inercia I_c=k·mr² siendo k=1 para un cuerpo en forma de un aro, k=1/2 para un cilindro o disco y k=2/5 para una esfera.

${\displaystyle -F_{r}r=\left(k·m{r}^2\right)\frac{d^2\phi }{d{t}^2}}$

La aceleración angular es negativa, disminuye la velociad angular y también la aceleración a_c. Teniendo en cuenta la relación entre aceleraciones, a_c=αr, sumamos las dos ecuaciones para eliminar F_r

${\displaystyle \left(k+1\right)\frac{d^{2}s}{d{t}^2}+g\sin \theta =0}$

Para una superficie cilíndrica de radio R, la relación entre el arco s que describe el c.m. y la posición angular θ del c.m. del cuerpo que rueda es, s=(R-r)θ. La ecuación diferencial del movimiento es

${\displaystyle \left(k+1\right)\left(R-r\right)\frac{d^2\theta }{d{t}^2}+g\sin \theta =0}$

Ecuaciones de Lagrange

La energía cinética del cuerpo que rueda es la suma de la energía cinética de traslación del centro de masa, con velocidad v_c y la energía cinética de rotación alrededor de un eje que pasa por el c.m. con velocidad angular dφ/dt

${\displaystyle \begin{array}{l}{E}_k=\frac{1}{2}m{\left(\frac{ds}{dt}\right)}^2+\frac{1}{2}\left(k·m{r}^2\right){\left(\frac{d\phi }{dt}\right)}^2=\frac{1}{2}m\left(k+1\right){\left(\frac{ds}{dt}\right)}^2=\\ \frac{1}{2}m\left(k+1\right){\left(R-r\right)}^2{\left(\frac{d\theta }{dt}\right)}^2\end{array}}$

La energía potencial, tomando como nivel cero, el eje de la superficie cilíndica es, -mg(R-r)cosθ

La lagrangiana L=E_k-E_p es

${\displaystyle L=\frac{1}{2}m\left(k+1\right){\left(R-r\right)}^2{\left(\frac{d\theta }{dt}\right)}^2+mg\left(R-r\right)\cos \theta }$

La ecuación del movimiento se obtiene

${\displaystyle \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0}$

El resultado es

${\displaystyle \begin{array}{l}m\left(k+1\right){\left(R-r\right)}^2\frac{d^2\theta }{d{t}^2}+mg\left(R-r\right)\sin \theta =0\\ \left(k+1\right)\left(R-r\right)\frac{d^2\theta }{d{t}^2}+g\sin \theta =0\end{array}}$

Cuando las oscilaciones son de amplitud pequeña, hacemos la aproximación, sinθ≈θ

El cuerpo que rueda sobre la superficie cilíndrica, describe aproximadamente un Movimiento Armónico Simple de frecuencia angular ω o periodo P=2π/ω

${\displaystyle {\omega }^2=\frac{g}{\left(k+1\right)\left(R-r\right)}}$

Superficie cóncava cualesquiera

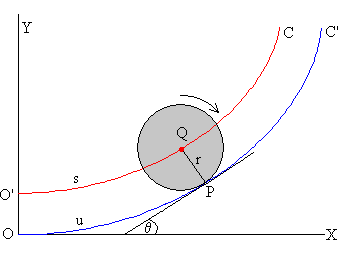
En la figura, se muestra la curva C’ sobre la que rueda el cuerpo redondo de radio r y la curva C que describe el centro de dicho cuerpo. La variable u mide el desplazamiento OP a lo largo de la curva C’. Mientras el c.m. se desplaza s a lo largo de la curva C, el cuerpo gira un ángulo φ.

El ángulo θ mide la pendiente de la recta tangente a la curva C’ en P

Movimiento de rotación y traslación del c.m.

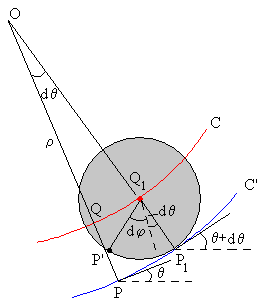
En la figura, vemos que en un intervalo de tiempo comprendido entre los instantes t y t+dt,

• el punto de contacto P se ha movido la distancia PP₁= du a lo largo de la curva C’,

• el c.m. se ha movido la distancia QQ₁=ds a lo largo de la curva C.

Si trazamos las tangentes a la curva C’ en los puntos P y P₁ y las normales a dichas direcciones, vemos que se cortan en un punto O denominado centro de curvatura, la distancia entre dicho punto y P o P₁ se denomina radio de curvatura ρ.

Movimiento de traslación del cuerpo.

El ángulo que forman las rectas tangentes dθ es igual al ángulo que forman las direcciones normales.

El arco PP₁ es igual al producto del radio OP por el ángulo comprendido dθ.

du=ρ· dθ

El arco QQ₁ es igual al producto del radio OQ por el ángulo comprendido dθ.

ds=(ρ-r)· dθ

Movimiento de rotación del cuerpo.

Ahora, nos fijamos en el movimiento de rotación en el intervalo de tiempo comprendido entre los instantes t y t+dt

Como el cuerpo rueda sin deslizar,  la longitud del arco PP₁=P₁P’=du. La pendiente de la curva se ha incrementado en dθ, el ángulo girado por el cuerpo en dicho intervalo dt de tiempo es

${\displaystyle d\phi =\frac{P_{1}P\text{'}}{r}-d\theta =\frac{du}{r}-d\theta }$

Eliminando dθ, tenemos las relaciones

${\displaystyle ds=\left(1-\frac{r}{\rho }\right)dud\phi =\frac{ds}{r}}$

Teniendo en cuenta esta última relación dφ=ds/r, la ecuación del movimiento del cuerpo que rueda se obtiene eliminando F_r, es decir, sumando la ecuación del movimiento de traslación del c.m. y la de rotación alrededor de un eje que pasa por el c.m.

${\displaystyle \left(k+1\right)\frac{d^{2}s}{d{t}^2}+g\sin \theta =0}$

La trayectoria del centro de masas

Vamos a demostrar que cuando la trayectoria del centro de masas es una cicloide, el cuerpo que rueda sin deslizar describe un MAS.

El c.m. describe un Movimiento Armónico Simple (MAS) si la aceleración d²s/dt² es proporcional al desplazamiento s y de signo contrario a éste. Si escribimos

${\displaystyle \text{sin}\theta =\frac{s}{4R}}$

donde R es una constante con dimensiones de longitud que no es el radio r del cuerpo como veremos más adelante. El c.m. describe un MAS

${\displaystyle \frac{d^{2}s}{d{t}^2}+\frac{g}{4R(k+1)}s=0}$

de frecuencia angular y periodo

${\displaystyle {\omega }^2=\frac{g}{4R(k+1)}P=2\pi \sqrt{\frac{4R(k+1)}{g}}}$

Para una esfera k=2/5

${\displaystyle P=4\pi \sqrt{\frac{7R}{5g}}}$

Ecuación de la trayectoria C del centro de masas

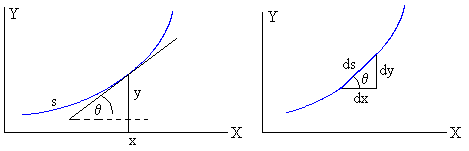
s=4R·sinθ
ds=4R·cosθ·dθ

dx=ds·cosθ=4Rcos²θ·dθ=2R(1+cos2θ)·dθ
dy=ds·sinθ=4R·sinθ·cosθ·dθ=2R·sin2θ·dθ

Integrando x e y con las condiciones iniciales θ=0, x=0, y=r.

x=R(2θ+sin2θ)
y=r+ R(1-cos2θ)

Estas son las ecuaciones paramétricas de una cicloide

Ecuación de la curva C' sobre la que que rueda el cuerpo

ds=4R·cosθ·dθ. De la relación entre ds y du y como du=ρ·dθ

${\displaystyle \begin{array}{l}\left(1-\frac{r}{\rho }\right)du=4R\cos \theta ·d\theta \\ \left(1-\frac{r}{\rho }\right)\rho ·d\theta =4R\cos \theta ·d\theta \end{array}}$

Obtenemos el valor del radio de curvatura ρ

ρ=r+4R·cosθ

La relación entre el desplazamiento infinitesimal du del punto P y la pendiente θ es

du=(r+4R·cosθ)·dθ

dx’=du·cosθ=(r·cosθ+4R·cos²θ)·dθ=(r·cosθ+2R·(1+cos2θ))·dθ
dy’=du·sinθ=(r·sinθ+4R· sinθ·cosθ)·dθ=(r·sinθ+2R· sin2θ)·dθ

Integrando x’ e y’ con las condiciones iniciales θ=0, x=0, y=0.

x’=r·sinθ+R(2θ+sin2θ)
y’=r(1-cosθ)+ R(1-cos2θ)

Esta no es la ecuación de una cicloide salvo que r→0

Representamos la pista y la trayectoria del centro de masas, una cicloide, utilizando código MATLAB

R=1;
r=0.25; %radio del cuerpo que rueda
hold on
fplot(@(t) r*sin(t)+R*(2*t+sin(2*t)), @(t) r*(1-cos(t))+R*(1-cos(2*t)),
[-pi/2,pi/2], 'linewidth',1.5, 'color','k') %pista
fplot(@(t) R*(2*t+sin(2*t)), @(t) r+R*(1-cos(2*t)),[-pi/2,pi/2]) %trayectoria c.m.
   
hold off
axis off
axis equal

Comprobación

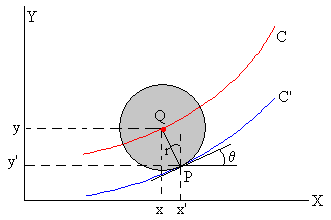
En la figura, vemos que al punto P(x’, y’) es un punto de la curva C’ le corresponde el punto Q(x, y) de la curva C. La relación entre x’ y x, y entre y e y’ es

x=x’-r·sinθ
y=y’+ r·cosθ

La curva C que describe el c.m. es una cicloide invertida (-π/2<θ< π/2) cuyo mínimo está en (0, r) y cuyo disco generador tiene un radio R. Sin embargo, la curva C’ sobre la que rueda el cuerpo no es una cicloide salvo que el radio del cuerpo sea r=0.

Movimiento Armónico Simple

Cuando un cuerpo describe un MAS su desplazamiento (en este caso el arco s) se expresa en función del tiempo de acuerdo con la ecuación.

s=A·sin(ω t+φ )

v_c=ω s₀·cos(ω t+φ)

Donde la amplitud A y la fase inicial φ se determina a partir de las condiciones iniciales, en nuestro caso t=0, s=s₀, v_c=0. La rueda parte de la posición s₀ con velocidad inicial cero.

s=s₀·sin(ω t+π/2)=s₀·cos(ω ·t)

La velocidad v_c del c.m. de la rueda se obtendrá derivando s respecto del tiempo

v_c=-ω s₀·sin(ω t)

Balance energético

El balance energético es similar al que efectuamos al estudiar el movimiento de un cuerpo que baja rodando por un plano inclinado.

Cuando la rueda se encuentra en la posición dada por el arco s a lo largo de la cicloide, o a una altura y sobre el origen. La energía potencial es

${\displaystyle \begin{array}{l}{E}_p=mgy=mgR(1-\cos 2\theta )=2mgR{\sin }^2\theta =\frac{mg}{8R}{s}^2\\ E_p=\frac{mg}{8R}{s}_0^2{\cos }^2(\omega t)\end{array}}$

La energía cinética es la suma de la energía cinética de traslación del c.m. y de rotación alrededor de un eje que pasa por c.m.

${\displaystyle E_k=\frac{1}{2}m{v}_c^2+\frac{1}{2}{I}_c{\omega }^2=\frac{1}{2}m(k+1){\omega }^2{s}_0^2{\sin }^2(\omega t)=\frac{mg}{8R}{s}_0^2{\sin }^2(\omega t)}$

donde se ha tenido en cuenta la relación entre ambas velocidades v_c=ω ·r para que ruede sin deslizar.

La suma de la energía cinética E_k y potencial E_p es constante e igual a

${\displaystyle E=E_k+E_p=\frac{mg}{8R}{s}_0^2}$

Actividades

Se introduce

• La posición inicial s₀ (longitud inicial del arco de la cicloide), en el control titulado Arco inicial
• El cuerpo que rueda, en el control titulado Cuerpo.
• El radio del disco que genera la cicloide se ha fijado en R=1 m, con ello queda fijada la forma de la superficie cóncava
• El radio del cuerpo redondo se ha fijado en r=0.4 m

Se pulsa el botón titulado Nuevo.

Observamos como el cuerpo rueda sin deslizar por un camino en forma de cicloide. La ecuación del movimiento es

s=s₀·cos(ω ·t)

Donde s es la longitud del arco de cicloide y ω la frecuencia angular del MAS

En la parte superior, se muestra el balance energético en un diagrama en forma de tarta. La energía potencial E_p y la energía cinética E_k como suma de la energía cinética de traslación del c.m. y de rotación alrededor de un eje que pasa por el c.m.

Braquistócrona en el campo gravitatorio terreste

En la página titulda Braquistócrona en el campo gravitatorio terreste, tratamos de encontrar la curva que hace que una partícula que cae bajo la acción de la gravedad, emplee un tiempo mínimo en recorrerla. Utilizaremos el cálculo de variaciones para obtener la ecuación de la curva que como vimos es una cicloide

En este apartado, se estudia un ejemplo similar. El centro de masas de una esfera que rueda sin deslizar bajo la acción de su peso, describe una cicloide.

Trayectoria del centro de la esfera

En la figura vemos una esfera de masa m y radio r que rueda sin deslizar a lo largo una pista de color azul paralela a la trayectoria del centro de la esfera (en color rojo). Vamos a demostrar que esta trayectoria del c.m. es una cicloide, pero la pista no lo es.

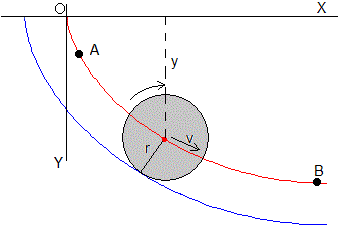
El centro de la esfera parte del reposo cuando coincide con el origen. Cuando el centro ha descendido una altura y, la velocidad de traslación del c.m. es v y la velocidad de rotación alrededor del un eje que pasa por el c.m. es v/r. La conservación de la energía se escribe

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}^2+\frac{1}{2}\left(\frac{2}{5}m{r}^2\right)\frac{v^2}{r^2}-mgy=0\\ v=\sqrt{\frac{10}{7}gy}\end{array}}$

El tiempo que tarda el centro de la esfera en desplazarse de A a B es

${\displaystyle I(y)=\underset{A}{\overset{B}{{\displaystyle \int }}}dt=\underset{A}{\overset{B}{{\displaystyle \int }}}\frac{ds}{v}=\sqrt{\frac{7}{10g}}\underset{A}{\overset{B}{{\displaystyle \int }}}\frac{\sqrt{1+{\dot{y}}^2}dx}{\sqrt{y}}}$

Aplicando la ecuación de Euler-Lagrange a la función f que no depende de x

${\displaystyle f(x,y,\dot{y})=\frac{\sqrt{1+{\dot{y}}^2}}{\sqrt{y}}}$

se obtiene las ecuaciones paramétricas de la curva denominada cicloide

${\displaystyle \{\begin{array}{l}x=R(\phi -\sin \phi )\\ y=R(1-\cos \phi )\end{array}}$

La pista sobre la que rueda la esfera

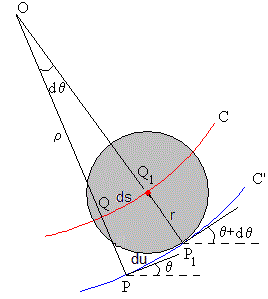
En la figura, vemos que en un intervalo de tiempo comprendido entre los instantes t y t+dt,

• el punto de contacto P se ha movido la distancia PP₁= du a lo largo de la pista C'

• el centro de la esfera se ha movido la distancia QQ₁=ds a lo largo de la curva C.

Si trazamos las tangentes a la curva C’ en los puntos P y P₁ y las normales a dichas direcciones, vemos que se cortan en un punto O denominado centro de curvatura, la distancia entre dicho punto y P o P₁ se denomina radio de curvatura ρ.

El ángulo que forman las rectas tangentes dθ es igual al ángulo que forman las direcciones normales.

El arco PP₁ es igual al producto del radio OP por el ángulo comprendido dθ.

du=ρ·dθ

El arco QQ₁ es igual al producto del radio OQ por el ángulo comprendido dθ.

ds=(ρ-r)·dθ

La longitud del arco ds entre Q y Q₁ es

${\displaystyle \begin{array}{l}ds=\sqrt{d{x}^2+d{y}^2}=\sqrt{R^2{\left(1-\cos \phi \right)}^{2}d{\phi }^2+R^2{\sin }^2\phi d{\phi }^2}=2R\sin \left(\frac{\phi }{2}\right)d\phi \\ \tan \theta =\frac{dy}{dx}=\frac{R\sin \phi ·d\phi }{R\left(1-\cos \phi \right)d\phi }=\frac{1}{\tan \left(\frac{\phi }{2}\right)}\theta =\frac{\pi }{2}-\frac{\phi }{2}\end{array}}$

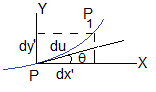
La longitud del arco du entre P y P₁ es

${\displaystyle du=ds+rd\theta =2R\sin \left(\frac{\phi }{2}\right)d\phi +\frac{r}{2}d\phi }$

Sus componentes son

${\displaystyle \begin{array}{l}dx\text{'}=\cos \theta ·du=\cos \left(\frac{\pi }{2}-\frac{\phi }{2}\right)du=\sin \left(\frac{\phi }{2}\right)du=\left(R\left(1-\cos \phi \right)+\frac{r}{2}\sin \left(\frac{\phi }{2}\right)\right)d\phi \\ dy\text{'}=\sin \theta ·du=\sin \left(\frac{\pi }{2}-\frac{\phi }{2}\right)du=\cos \left(\frac{\phi }{2}\right)du=\left(R\sin \phi +\frac{r}{2}\cos \left(\frac{\phi }{2}\right)\right)d\phi \end{array}}$

Integramos respecto del parámetro φ

${\displaystyle \begin{array}{l}x\text{'}=R\left(\phi -\sin \phi \right)-r\cos \left(\frac{\phi }{2}\right)+c_1\\ y\text{'}=-R\cos \phi +r\sin \left(\frac{\phi }{2}\right)+c_2\end{array}}$

Se determinan las constantes c₁ y c₂ sabiendo que para φ=0, x'=-r e y'=0

Las ecuaciones paramétricas de la pista sobre la que rueda la esfera son

${\displaystyle \{\begin{array}{l}x\text{'}=R\left(\phi -\sin \phi \right)-r\cos \left(\frac{\phi }{2}\right)\\ y\text{'}=R\left(1-\cos \phi \right)+r\sin \left(\frac{\phi }{2}\right)\end{array}}$

Vamos a determinar el valor del parámetro R para que el centro de la esfera pase por el punto (x₁, y₁). Para ello, hay que calcular la raíz φ₁ de la ecuación trascendente

${\displaystyle \frac{y_1}{x_1}=\frac{R\left(1-\cos {\phi }_1\right)}{R\left(\phi -\sin {\phi }_1\right)}}$

Conocidos y₁ y φ₁ calculamos R,

${\displaystyle R=\frac{y_1}{1-\cos {\phi }_1}}$

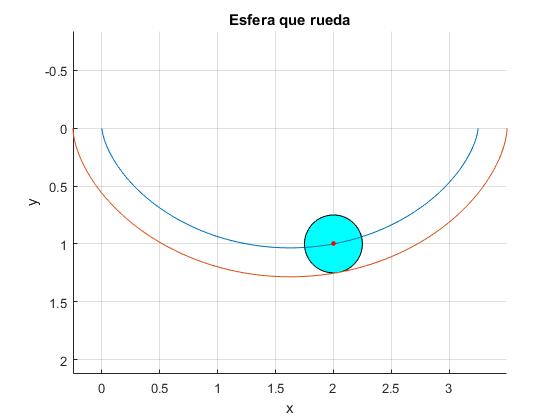
Calculamos el parámetro R de la trayectoria del centro de la esfera, sabiendo que pasa por el punto (x₁=2, y₁=1). Representamos la trayectoria del c.m. y la pista sobre la que rueda sin deslizar una esfera de radio r=0.25

x1=2; %punto
y1=1;
r=0.25; %radio
hold on
f=@(x) (1-cos(x))/(x-sin(x))-y1/x1;
phi=fzero(f,pi);
R=y1/(1-cos(phi)); %parámetro R
ang=(1:360)*pi/180; %esfera
fill(x1+r*cos(ang),y1+r*sin(ang),'c') %la Tierra
%cicloide
fplot(@(th) R*(th-sin(th)),@(th) R*(1-cos(th)),[0,2*pi])
%pista
fplot(@(th) R*(th-sin(th))-r*cos(th/2),@(th) R-R*cos(th)+r*sin(th/2),[0,2*pi])
plot(x1,y1,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
set (gca,'Ydir','reverse')
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Esfera que rueda')

Tiempo que tarda la esfera en discribir un arco de cicloide

Supongamos que la esfera parte del reposo desde el punto A (x₀, y₀), vamos a calcular el tiempo que tarda en llegar al punto B

El principio de conservación de la energía se escribe

${\displaystyle \begin{array}{l}-mg{y}_0=\frac{1}{2}m{v}^2+\frac{1}{2}\left(\frac{2}{5}m{r}^2\right)\frac{v^2}{r^2}-mgy\\ v=\sqrt{\frac{10}{7}g(y-y_0)}\end{array}}$

Calculamos el tiempo T que tarda en desplazarse entre dos puntos A y B

${\displaystyle \begin{array}{l}T=\underset{A}{\overset{B}{{\displaystyle \int }}}\frac{ds}{v}=\sqrt{\frac{7}{10g}}\underset{A}{\overset{B}{{\displaystyle \int }}}\frac{\sqrt{1+{\dot{y}}^2}dx}{\sqrt{y-y_0}}\\ T=\sqrt{\frac{7}{10g}}\underset{A}{\overset{B}{{\displaystyle \int }}}\frac{\sqrt{1+{\left(\frac{\sin \phi }{1-\cos \phi }\right)}^2}R\left(1-\cos \phi \right)d\phi }{\sqrt{R\left(1-\cos \phi \right)-R\left(1-\cos {\phi }_0\right)}}=\sqrt{\frac{7R}{10g}}\underset{A}{\overset{B}{{\displaystyle \int }}}\frac{2\sin \left(\frac{\phi }{2}\right)}{\sqrt{\cos {\phi }_0-\cos \phi }}d\phi =\\ \sqrt{\frac{7R}{10g}}\underset{A}{\overset{B}{{\displaystyle \int }}}\frac{2\sin \left(\frac{\phi }{2}\right)}{\sqrt{2{\cos }^2\left({\phi }_0/2\right)-2{\cos }^2\left(\phi /2\right)}}d\phi \end{array}}$

Haciendo el cambio z=cos(φ/2)/cos(φ₀/2)

${\displaystyle \begin{array}{l}T=-2\sqrt{\frac{7R}{5g}}\underset{A}{\overset{B}{{\displaystyle \int }}}\frac{dz}{\sqrt{1-z^2}}dz={2\sqrt{\frac{7R}{5g}}\arccos \left(\frac{\cos \left(\phi /2\right)}{\cos \left({\phi }_0/2\right)}\right)|}_{{\phi }_0}^{\phi }=\\ 2\sqrt{\frac{7R}{5g}}\arccos \left(\frac{\cos \left(\phi /2\right)}{\cos \left({\phi }_0/2\right)}\right)\end{array}}$

Si A es el origen φ₀=0 y si B es el punto (x₁, y₁), calculamos la raíz φ₁ de la ecuación trascendente y después, el parámetro R, tal como hemos hecho anteriormente

El tiempo T que tarda en llegar la partícula al punto B describiendo un arco de cicloide, partiendo del origen en reposo es

${\displaystyle T=\sqrt{\frac{7R}{5g}}{\phi }_1}$

x1=2; %punto
y1=1;
r=0.25; %radio
f=@(x) (1-cos(x))/(x-sin(x))-y1/x1;
phi=fzero(f,pi);
R=y1/(1-cos(phi)); %parámetro R
T=sqrt(7*R/(5*9.8))*phi; %tiempo
disp(T);

   0.9536

El periodo de la oscilación es 4 veces el tiempo que tarda en ir de A, φ₀=0 a B, φ₁=π (punto más bajo de la trayectoria)

${\displaystyle P=4\pi \sqrt{\frac{7R}{5g}}}$

Que es el resultado obtenido en el primer apartado

Referencias

Gillespie D. T. Simple harmonic motion of a round body rolling on a concave curve. Am. J. Phys. 52 (2) February 1984, pp. 180-182.

Eric Rodgers. Brachistochrone and Tautochrone Curves for Rolling Bodies. Am. J. Phys. 1946, pp. 249-252