Cilindro macizo que rueda por encima de un tubo que rueda sobre un plano horizontal.
Superficie cilíndrica fija
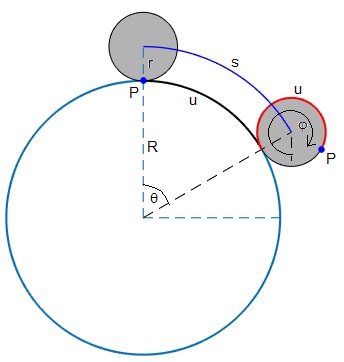
Un cuerpo cilíndrico de radio r rueda sin deslizar sobre la superficie exterior de un tubo radio R. El centro del cuerpo describe un arco s=(R+r)θ (en color azul), mientras el cuerpo rueda una longitud u=Rθ sobre la pista (en color negro) e igual al arco de color rojo pintado sobre el cuerpo
En la figura, se señala la posición inicial del punto P del cilindro macizo y su posición angular en el instante t, φ=u/r+θ=Rθ/r+θ
Parte de la figura ha sido elaborada con el siguiente código
th=pi/3; %ángulo r=0.25; %radio del cuerpo que rueda hold on fplot(@(t) cos(t), @(t) sin(t), [0,2*pi], 'linewidth',1.5) ang=(1:360)*pi/180; x1=r*cos(ang); y1=(1+r)+r*sin(ang); fill(x1,y1,[0.7 0.7 0.7]) line([0,0],[0,1+r],'linestyle','--') line([0,1],[0,0],'linestyle','--') x1=(1+r)*sin(th)+r*cos(ang); y1=(1+r)*cos(th)+r*sin(ang); fill(x1,y1,[0.7 0.7 0.7]) line([0,(1+r)*sin(th)],[0,(1+r)*cos(th)],'linestyle','--','color','k') fplot(@(t) cos(t), @(t) sin(t), [pi/2-th,pi/2,], 'linewidth',1.5,'color','k') fplot(@(t) (1+r)*sin(th)+r*cos(t), @(t) (1+r)*cos(th)+r*sin(t), [-th/r-(pi/2+th),-(pi/2+th)], 'linewidth',1.5, 'color','r') fplot(@(t) (1+r)*cos(t), @(t) (1+r)*sin(t), [pi/2-th, pi/2], 'linewidth',1, 'color','b') plot(0,1,'bo','linewidth',1,'markersize',4,'markeredgecolor','b', 'markerfacecolor','b') plot((1+r)*sin(th)+r*cos(-th/r-(pi/2+th)),(1+r)*cos(th)+r*sin(-th/r-(pi/2+th)), 'bo','linewidth',1,'markersize',4,'markeredgecolor','b', 'markerfacecolor','b') hold off axis equal axis off
Superficie cilíndrica móvil
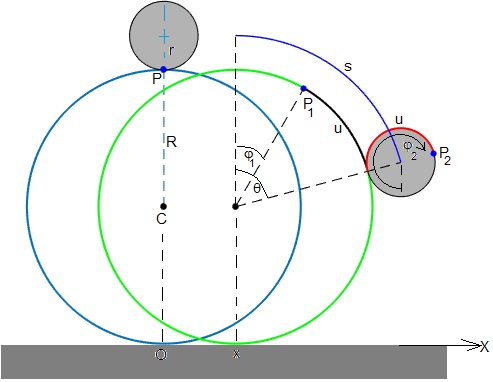
La superficie cilíndrica de radio R, rueda sin deslizar sobre el plano horizontal, en un tiempo t, su centro C se desplaza x y gira alrededor de un eje que pasa por su centro un ángulo φ1=x/R, el punto P de la superficie cilíndrica se convierte en el punto P1. Un cilindro macizo de radio r rueda sin deslizar sobre la superficie cilíndrica exterior de radio R. En el instante t=0, el cilindro está situado en el origen, tal como se indica en la parte izquierda de la figura.
El centro del cilindro macizo se ha desplazado un arco s (en color azul), el cilindro macizo rueda sin deslizar un arco u sobre la superficie cilíndica. La posición angular θ del centro del cilindro macizo, medida desde el origen, θ=u/R+φ1 o bien, u=R(θ-φ1).
El punto de contacto P sobre la superficie del cilindro macizo se ha convertido en el punto P2, ha girado un ángulo u/r, su posición angular es φ2=u/r+θ.
Parte de la figura ha sido elaborada con el siguiente código
r=0.25; %radio del cuerpo que rueda hold on %pista fplot(@(t) cos(t), @(t) sin(t), [0,2*pi], 'linewidth',1.5) %cuerpo ang=(1:360)*pi/180; x1=r*cos(ang); y1=(1+r)+r*sin(ang); fill(x1,y1,[0.7 0.7 0.7]) line([0,0],[0,1],'linestyle','--') plot(0,0,'bo','linewidth',1,'markersize',4,'markeredgecolor','k', 'markerfacecolor','k') plot(0,1,'bo','linewidth',1,'markersize',4,'markeredgecolor', 'b','markerfacecolor','b') %pista aGira=pi/6; th=pi/4+aGira; %ángulo fplot(@(t) aGira+cos(t), @(t) sin(t), [0,2*pi], 'linewidth',1.5,'color','g') x1=aGira+(1+r)*sin(th)+r*cos(ang); y1=(1+r)*cos(th)+r*sin(ang); fill(x1,y1,[0.7 0.7 0.7]) line([aGira,aGira+(1+r)*sin(th)],[0,(1+r)*cos(th)],'linestyle','--', 'color','k') fplot(@(t) aGira+cos(t), @(t) sin(t), [(pi/2-th),pi/2-aGira], 'linewidth',1.5,'color','k') fplot(@(t) aGira+(1+r)*sin(th)+r*cos(t), @(t) (1+r)*cos(th)+r*sin(t), [-pi/2-th-(th-aGira)/r, -pi/2-th], 'linewidth',1.5, 'color','r') fplot(@(t) aGira+(1+r)*cos(t), @(t) (1+r)*sin(t), [(pi/2-th),pi/2], 'linewidth',1,'color','b') plot(aGira+sin(aGira),cos(aGira),'bo','markersize',4,'markeredgecolor', 'b','markerfacecolor','b') plot(aGira+(1+r)*sin(th)+r*cos(-pi/2-th-(th-aGira)/r),(1+r)*cos(th)+ r*sin(-pi/2-th-(th-aGira)/r),'bo','markersize',4,'markeredgecolor', 'b','markerfacecolor','b') plot(aGira,0,'bo','linewidth',1,'markersize',4,'markeredgecolor','k', 'markerfacecolor','k') line([aGira,aGira],[0,1+r],'linestyle','--','color','k') line([aGira,aGira+sin(aGira)],[0,cos(aGira)],'linestyle','--','color','k') hold off axis equal axis off
Posición y velocidad del centro del cilindro macizo
La posición del centro del cilindro macizo y las componentes de su velocidad son
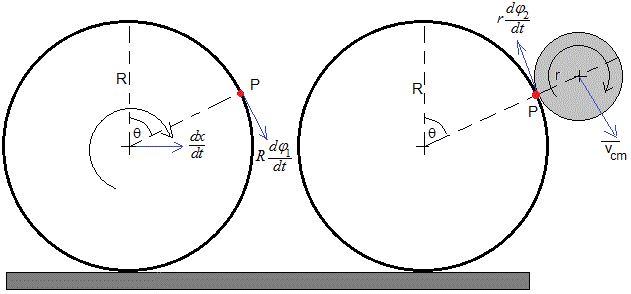
Calculamos la velocidad del punto P de contacto entre el cilindro macizo y el tubo.
En la figura de la izquierda, la velocidad del punto P situado en la posición angular θ en la superficie exterior del tubo de radio R, es la suma de la velocidad de traslación del c.m. dx/dt y de rotación alrededor de un eje que pasa por el centro Rdφ1/dt. Sus componentes son
En la figura de la derecha, la velocidad del punto de contacto P es la suma de la velocidad del centro del cilindro macizo cuyas componentes ya hemos calculado y la velocidad de rotación alrededor de un eje que pasa por el centro del cilindro macizo rdφ2/dt. Las componentes son
Teniendo en cuenta la relación entre φ2, θ y φ1 establecida en el apartado anterior
El punto P está en reposo en el sistema de referencia que se mueve con el tubo. Que es la condición para que el cilindro macizo ruede sin deslizar sobre la superficie exterior del tubo
Energía del sistema
La energía potencial del centro del cilindro macizo de masa m y radio r es
La energía cinética del tubo cilíndrico de masa M y radio R es
La energía cinética del cilindro macizo de masa m y radio r es
Ep=mg(R+(R+r)cosθ)
La energía total en cada instante t se conserva y es igual a la energía inicial
Ecuación del movimiento
La lagrangiana, L=Ek1+Ek2-Ep es
La primera ecuación del movimiento es
La lagrangiana L no depende de φ1, tenemos una constante del movimiento
Denominamos ω0 a dicha constante
Integramos esta ecuación, con las condiciones iniciales: en el instante t=0, θ=θ0, φ1=0.
La posición del centro del tubo es x=R·φ1
Sustituyendo d2φ1/dt2, en la primera ecuación del movimiento
obtenemos
Una ecuación similar a la obtenida en la página titulada Cilindro macizo que rueda en el interior de un tubo que a su vez, rueda en un plano horizontal, salvo el signo del último término, el signo positivo da un carácter oscilatorio a la solución y el signo negativo no lo da
Fuerzas sobre los dos cuerpos
En la página titulada Una esfera rueda sobre una cúpula semiesférica analizamos las tres fases del movimiento de la esfera. En la última, la esfera deja de estar en contacto con la cúpula, cuando la reacción N de la superficie se hace cero, y la esfera comienza a describir una trayectoria parabólica
En este caso, supondremos que el cilindro macizo rueda sin deslizar a lo largo de la superficie exterior del tubo que a su vez, rueda sin deslizar a lo largo del plano horizontal, hasta que la reacción N21 de la superficie se hace cero
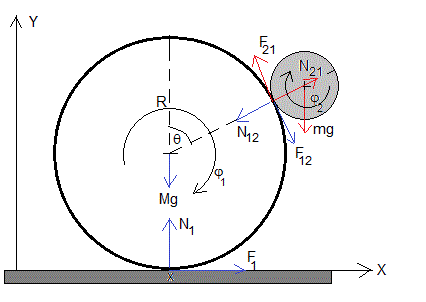
En la figura, se han dibujado las fuerzas que actúan sobre el cilindro macizo (en color rojo) y las fuerza sobre el tubo (en color azul)
- El peso Mg en el centro del tubo y mg en el centro del cilindro macizo
- La reacción del plano horizontal, N1
- La fuerza de rozamiento entre el plano horizontal y el tubo en el punto de contacto, F1
- La fuerza N12 que ejerce el cilindro macizo sobre el tubo en el punto de contacto, que es igual y de sentido contrario a la que ejerce el tubo sobre el cilindro macizo N21
- La fuerza de rozamiento F12 que ejerce la superficie del cilindro macizo sobre el tubo en el punto de contacto, que será igual y de sentido contrario a la que ejerce la superficie del tubo sobre el cilindro F21
El movimiento del centro de masas del sistema solamente depende de las fuerzas exteriores al sistema: N1, F1, mg y Mg
En el instante t, el centro del tubo se ha desplazado x horizontalmente y la posición angular del centro del cilindro macizo es θ, tal como se muestra en la figura
La posición del centro de masas del sistema formado por el tubo de masa M y radio R y el cilindro macizo de masa m y radio r es
La velocidad y aceleración del centro de masas son, respectivamente
La ecuación del movimiento del centro de masas en la dirección horizontal es
-
La ecuación del movimiento del centro de masas en la dirección vertical es
-
La ecuación de la dinámica de rotación del tubo alrededor de un eje que pasa por el centro es
-
La ecuación de la dinámica de rotación del cilindro macizo alrededor de un eje que pasa por el centro es
El tubo está en equilibrio en la dirección vertical
El centro del tubo se mueve horizontalmente con aceleración d2x/dt2
Eliminamos F12 entres las dos últimas ecuaciones. Multiplicamos por cosθ la primera y por sinθ la segunda y sumamos
Introducimos las expresiones de N1 y F1. El resultado es
Introducimos la expresión de d2φ1/dt2. El resultado es
La reacción de la superficie del tubo, N12 se hace cero en el instante ts, el centro del tubo ocupa la posición xs y el centro del cilindro macizo, la posición angular θs
Trayectoria parabólica
Cuando la reacción de la superficie del tubo N12 se hace cero, el centro del cilindro macizo describe una trayectoria parabólica desde la posición inicial y con la velocidad inicial
Las ecuaciones de la trayectoria parabólica son
Solución numérica
Para determinar la posición θ del centro del cilindro macizo en función del tiempo t, se resuelve la ecuación diferencial
con las siguientes condiciones iniciales: en el instante t=0, θ0=0, φ1=0, dθ/dt=(dθ/dt)0=0.01, dφ1/dt=0.
La constante del movimiento ω0 vale
La posición x=R·φ1 del centro del tubo, o el ángulo girado φ1 se obtienen de la expresión
Creamos un script para resolver mediante ode45 de MATLAB la eucación diferencial para obtener la posición angular θ del centro del cilindro macizo en función del tiempo t y posteriormente, la posición x=Rφ1 del centro del tubo y el ángulo girado φ1 en función del tiempo t. El proceso de cálculo se interrumpe cuando la reacción de la superficie del tubo N12=0 se hace cero, el cilindro macizo cae
El cilindro parte del origen y se le proporciona una pequeña velocidad angular inicial
R=1; %radio superficie cilíndrica
r=0.25; %radio cilindro macizo
M=1; %masa superficie cilíndrica
m=2; %masa cilindro macizo
wCilindro=0.01; %velocidad angular inicial
th_0=0; %posición angular inicial
w0=m*(1+r/R)*(2*cos(th_0)-1)*wCilindro/(3*m+4*M);
x0=[th_0,wCilindro];
f=@(t,x) [x(2); -2*(2*cos(x(1))-1)*sin(x(1))*m*x(2)^2/(3*(3*m+4*M)-
(2*cos(x(1))-1)^2*m)+2*9.8*sin(x(1))*(3*m+4*M)/((R+r)*(3*(3*m+4*M)-
(2*cos(x(1))-1)^2*m))];
opts=odeset('events',@(t,x) stop_cilindro3(t,x,m,M,r,R));
[t,x]=ode45(f,[0,50],x0,opts);
phi_1=w0*t-m*(1+r/R)*(2*sin(x(:,1))-x(:,1)-2*sin(th_0)+th_0)/(3*m+4*M);
vPhi=w0-m*(1+r/R)*(2*cos(x(:,1))-1).*x(:,2)/(3*m+4*M);
hold on
plot(t,x(:,1),'r') %cilindro macizo
plot(t,phi_1,'b') %tubo
hold off
grid on
xlabel('t')
ylabel('\theta,\phi_1')
title('Movimiento de los cilindros')
Se define la función stop_cilindro3 para detener el proceso de integración cuando N12=0
function [value,isterminal,direction]=stop_cilindro3(~,x,m,M,r,R)
acel=-2*(2*cos(x(1))-1)*sin(x(1))*m*x(2)^2/(3*(3*m+4*M)-(2*cos(x(1))-1)^2*m)+
2*9.8*sin(x(1))*(3*m+4*M)/((R+r)*(3*(3*m+4*M)-(2*cos(x(1))-1)^2*m));
temp=m*9.8*cos(x(1))+m^2*(R+r)*(2*sin(x(1))*x(2)^2-(2*cos(x(1)))*acel)*sin(x(1))
/(3*m+4*M)-m*(R+r)*x(2)^2;
value=temp;
isterminal=1;
direction=0;
end
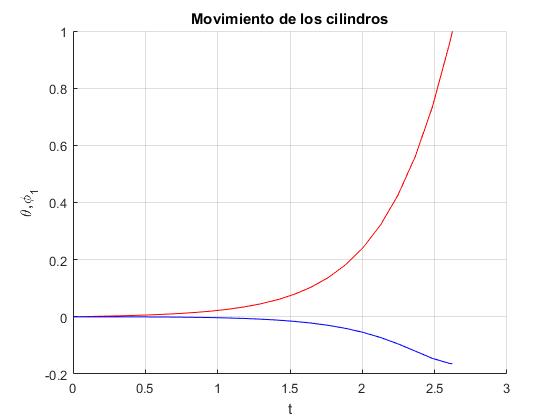
En rojo, la posición angular θ del cilindro macizo, en azul, la del tubo, φ1
El instante final, la posición final del cilindro macizo y del tubo son, respectivamente
>> t(end) ans = 2.6229 >> x(end,1) ans = 0.9996 >> phi_1(end) ans = -0.1642
El cilindro macizo se mueve hacia adelante y el tubo hacia atrás
Comprobamos que la energía inicial, es aproximadamente igual a la energía en cada instante
E0=3*m*(R+r)^2*wCilindro^2/4+m*9.8*(R+(R+r)*cos(th_0))
E0 = 44.1002
>> vPhi=w0-m*(1+r/R)*(2*cos(x(:,1))-1).*x(:,2)/(3*m+4*M);
>> E=3*m*(R+r)^2*x(:,2).^2/4+(3*m/4+M)*R^2*vPhi.^2+m*(R+r)*R*(2*cos(x(:,1))-1).
*x(:,2).*vPhi/2+m*9.8*(R+(R+r)*cos(x(:,1)))
E =
44.1002
44.1002
......
44.1062
44.1064
44.1066
Actividades
Se introduce
- La masa m del cilindro macizo, en el control titulado Masa cilindro macizo
Se ha fijado
- La masa M=1 y el radio R=1, del tubo que rueda sobre el plano horizontal
- El radio r=0.25 del cilindro macizo
- La posición angular inicial del centro del cilindro macizo θ0=0, se ha fijado en el origen
- La velocidad angular inicial del centro del cilindro macizo (dθ/dt)0=0.01, se proporciona una pequeña velocidad angular inicial
Se pulsa el botón titulado Nuevo
Se muestra el tubo de masa M y radio r rodando en el plano horizontal y el cilindro macizo de masa m y radio r rodando sin deslizar en su superficie interior
Se proporcionan los siguientes datos hasta que el cilindro macizo cae de
- El tiempo t
- La posición x=Rφ1 y velocidad dx/dt=R·dφ1/dt del centro del tubo
- La posición angular θ y la velocidad angular dθ/dt del cilindro macizo
El programa calcula en cada instante el tanto por ciento de error relativo en la energía o el cociente
donde E es la energía del sistema en cualquier instante t, y E0 es la energía inicial del sistema.
Este valor se proporciona en caracteres de color rojo en la parte izqiuerda. Su valor debe ser siempre cero, o un valor muy pequeño lo que indica que la energía del sistema permanece constante y el programa realiza los cálculos correctamente.
Referencias
Kirk T. McDonald. Cylinder Rolling on Another Rolling Cylinder.http://physics.princeton.edu/~mcdonald/examples/2cylinders.pdf .

