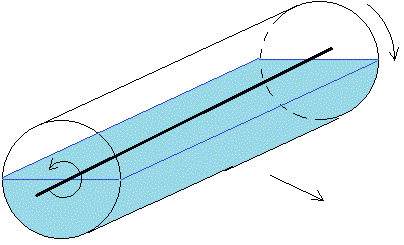
Cuando se llena un cubo de agua y se hace girar, el agua tarda un tiempo en adquirir la misma velocidad angular que el recipiente, esto es debido a que la viscosidad del agua no es grande. Durante el tiempo de observación del movimiento de la botella medio llena de agua, supondremos que el agua se comporta como un sólido rígido que gira alrededor del eje de simetría de la botella, sin interacción alguna entre dos cuerpos

Supondremos también, que la botella rueda sin deslizar a lo largo del plano horizontal o inclinado.

Centro de masas del agua

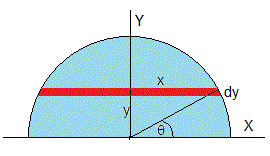
Calculamos el centro de masas de una figura plana homogénea en forma de semicírculo de radio R

Situamos el origen en el centro del semicírculo y los ejes X e Y como se indica en la figura. Por simetría, el centro de masas estará en el eje Y, x_cm=0

Sea σ la densidad superficial (masa por unidad de área) de la placa semicircular. Consideremos una franja, de anchura dy, y de longitud 2x paralela al eje X, marcada en color rojo en la figura. Su masa es dm=σ(2x·dy). La posición y_cm del centro de masas es

${\displaystyle y_{cm}=\frac{{\displaystyle \int ydm}}{{\displaystyle \int dm}}=\frac{{\displaystyle \underset{0}{\overset{R}{\int }}y\left(\sigma 2\sqrt{R^2-y^2}dy\right)}}{{\displaystyle \underset{0}{\overset{R}{\int }}\sigma 2\sqrt{R^2-y^2}dy}}=\frac{\sigma {\displaystyle \underset{0}{\overset{R}{\int }}\left(\sqrt{R^2-y^2}\right)2y·dy}}{\sigma \frac{1}{2}\pi R^2}=\frac{\frac{2}{3}{R}^3}{\frac{1}{2}\pi R^2}=\frac{4R}{3\pi }}$

La integral de numerador es inmediata, la del denominador es el área de un semicírculo, πR²/2, que se puede calcular expresando y en coordenadas polares, y=Rsinθ, dy=Rcosθ·dθ

${\displaystyle {\displaystyle \underset{0}{\overset{R}{\int }}2\sqrt{R^2-y^2}dy={\displaystyle \underset{0}{\overset{\pi /2}{\int }}2R^2{\cos }^2\theta ·d\theta =R^2}}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\left(1+\cos (2\theta )\right)d\theta =}\frac{1}{2}\pi R^2}$

Momento de inercia del agua

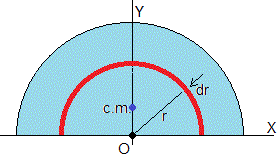
Sea un cilindro homogéneo de radio R cortado por la mitad cuya masa es m

Tomamos un elemento diferencial de masa comprendido entre r y r+dr. La masa de este elemento es

${\displaystyle \frac{m}{\pi R^2/2}\pi r·dr=\frac{2m}{R^2}r·dr}$

El momento de inercia respecto de un eje perpendicular al plano de la figura y que pasa por O es

${\displaystyle {\displaystyle \underset{0}{\overset{R}{\int }}{r}^2\left(\frac{2m}{R^2}r·dr\right)}=\frac{2m}{R^2}{\displaystyle \underset{0}{\overset{R}{\int }}{r}^{3}dr=\frac{1}{2}m{R}^2}}$

El momento de inercia respecto a un eje perpendicular al plano de la figura y que pasa por el centro de masas, I_cm es

${\displaystyle \frac{1}{2}m{R}^2=I_{cm}+m{y}_{cm}^2}$

Movimiento de la botella medio llena en el plano horizontal

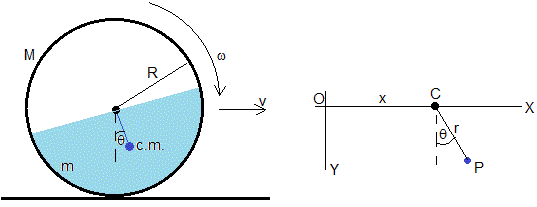
Designaremos por r=4R/(3π), la posición del centro de masas del medio cilindro de agua

En un instante dado, la posición del centro del cilindro C es x, y=0. La posición del centro de masas del agua P es

x_P=x+rsinθ
y_P=rcosθ

Derivamos con respecto del tiempo para obtener la velocidad

${\displaystyle \begin{array}{l}\frac{d{x}_p}{dt}=\frac{dx}{dt}+r\cos \theta \frac{d\theta }{dt}\\ \frac{d{y}_p}{dt}=-r\sin \theta \frac{d\theta }{dt}\end{array}}$

Energía cinética

Calculamos la energía cinética de un cilindro hueco de masa M y radio R que gira alrededor de su eje de simetría con velocidad angular ω y cuyo centro de masas se desplaza con velocidad dx/dt. Téngase en cuenta, que el momento de inercia de un cilindro hueco de masa M y radio R respecto de su eje de simetría es MR²

${\displaystyle \frac{1}{2}M{\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}\left(M{R}^2\right){\omega }^2}$

Si el cilindro rueda sin deslizar, dx/dt=Rω. La energía cinética total del cilindro hueco es

${\displaystyle M{\left(\frac{dx}{dt}\right)}^2}$

La energía cinética del agua se compone también de dos términos. La energía cinética del centro de masas

${\displaystyle \frac{1}{2}m\left({\left(\frac{d{x}_p}{dt}\right)}^2+{\left(\frac{d{y}_p}{dt}\right)}^2\right)=\frac{1}{2}m\left({\left(\frac{dx}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2+2r\frac{dx}{dt}\frac{d\theta }{dt}\cos \theta \right)}$

y la energía cinética de rotación alrededor de un eje paralelo al eje de simetría que pasa por el centro de masas con velocidad angular dθ/dt

${\displaystyle \frac{1}{2}{I}_{cm}{\left(\frac{d\theta }{dt}\right)}^2}$

La energía cinética total es

${\displaystyle \begin{array}{l}T=M{\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}m\left({\left(\frac{dx}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2+2r\frac{dx}{dt}\frac{d\theta }{dt}\cos \theta \right)+\frac{1}{2}{I}_{cm}{\left(\frac{d\theta }{dt}\right)}^2=\\ \frac{1}{2}(2M+m){\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}\left(\frac{1}{2}m{R}^2\right){\left(\frac{d\theta }{dt}\right)}^2+mr\frac{dx}{dt}\frac{d\theta }{dt}\cos \theta \end{array}}$

Energía potencial

Tomando como origen el punto O, la energía potencial del centro del cilindro es cero y la del centro de masa del agua, V=-mgrcosθ

Ecuaciones del movimiento

La lagrangiana de este sistema es

${\displaystyle L=T-V=\frac{1}{2}(2M+m){\left(\frac{dx}{dt}\right)}^2+mr\frac{dx}{dt}\frac{d\theta }{dt}\cos \theta +\frac{1}{4}m{R}^2{\left(\frac{d\theta }{dt}\right)}^2+mgr\cos \theta }$

Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right)-\frac{\partial L}{\partial x}=0\\ (2M+m)\frac{d^{2}x}{d{t}^2}+mr\frac{d^2\theta }{d{t}^2}\cos \theta -mr{\left(\frac{d\theta }{dt}\right)}^2\sin \theta =0\\ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \frac{1}{2}{R}^2\frac{d^2\theta }{d{t}^2}+r\frac{d^{2}x}{d{t}^2}\cos \theta +gr\sin \theta =0\end{array}}$

En este sistema de dos ecuaciones, despejamos las derivadas segundas, respecto del tiempo

${\displaystyle \begin{array}{l}\left(2M+m-\frac{2m{r}^2}{R^2}{\cos }^2\theta \right)\frac{d^{2}x}{d{t}^2}-\frac{2m{r}^2}{R^2}g\cos \theta \sin \theta -mr{\left(\frac{d\theta }{dt}\right)}^2\sin \theta =0\\ \left(\frac{1}{2}{R}^2-\frac{m{r}^2}{2M+m}{\cos }^2\theta \right)\frac{d^2\theta }{d{t}^2}+\frac{m{r}^2}{2M+m}{\left(\frac{d\theta }{dt}\right)}^2\cos \theta \sin \theta +gr\sin \theta =0\end{array}}$

Aproximaciones

Si θ y dθ/dt son pequeños, hacemos las siguientes aproximaciones: cosθ≈1, sinθ≈θ, (dθ/dt)²sinθ≈0. El sistema de dos ecuaciones se reduce a

${\displaystyle \begin{array}{l}\left(2M+m-\frac{2m{r}^2}{R^2}\right)\frac{d^{2}x}{d{t}^2}-\frac{2m{r}^2}{R^2}g\theta =0\\ \left(\frac{1}{2}{R}^2-\frac{m{r}^2}{2M+m}\right)\frac{d^2\theta }{d{t}^2}+gr\theta =0\end{array}}$

La segunda ecuación diferencial es conocida, se trata de un Movimiento Armónico Simple, de frecuencia angular Ω

${\displaystyle \begin{array}{l}\frac{d^2\theta }{d{t}^2}+{\Omega }^2\theta =0{\Omega }^2=\frac{2(2M+m)r}{(2M+m)R^2-2m{r}^2}g\\ \theta =A\sin (\Omega t)+B\cos (\Omega t)\end{array}}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales. En el instante t=0, θ=0, y dθ/dt=(dθ/dt)₀, la velocidad angular inicial es distinta de cero

${\displaystyle \theta =\frac{1}{\Omega }{\left(\frac{d\theta }{dt}\right)}_0\sin (\Omega t)}$

Estas condiciones iniciales se pueden conseguir haciendo chocar la botella medio llena de agua con una pared vertical, en el instante de choque el agua se desplaza como se muestra en al figura

Conocida la solución de la segunda ecuación diferencial, θ(t), buscamos una solución de la primera x(t) que es la posición del centro de la botella

${\displaystyle \begin{array}{l}\left(2M+m-\frac{2m{r}^2}{R^2}\right)\frac{d^{2}x}{d{t}^2}-\frac{2m{r}^2}{R^2}g\frac{1}{\Omega }{\left(\frac{d\theta }{dt}\right)}_0\sin (\Omega t)=0\\ \frac{d^{2}x}{d{t}^2}=\frac{mr\Omega }{2M+m}{\left(\frac{d\theta }{dt}\right)}_0\sin (\Omega t)\end{array}}$

Integramos la ecuación diferencial, para obtener la velocidad del centro de la botella, dx/dt, sabiendo que en instante t=0, parte del reposo, dx/dt=0

${\displaystyle \frac{dx}{dt}=\frac{mr}{2M+m}{\left(\frac{d\theta }{dt}\right)}_0\left(1-\cos (\Omega t)\right)}$

Ejemplo

Sea el radio del cilindro hueco R=50 mm, su masa M=1.74 kg, la masa de agua m=0.91 kg. La posición del centro de masas del agua es r=4R/(3π)

Integramos el sistema de dos ecuaciones diferenciales, con las condiciones iniciales t=0, θ=0, dθ/dt=1. El centro del cilindro hueco parte del origen en reposo, x=0, dx/dt=0

Elaboramos un script para repesentar la velocidad dx/dt del centro del cilindro hueco en función del tiempo t y compararlos con la aproximación para ángulos pequeños

R=50/1000; %radio de la botella
M=0.91; %masa botella
m=1.74; %masa del agua

r=4*R/(3*pi); %posición del c.m. del agua
Omega=sqrt(2*(2*M+m)*r*9.8/((2*M+m)*R^2-2*m*r^2)); %frecuencia angular
u=1; %velocidad angular inicial
x0=[0,0,0,u];
%sistema de dos ecuaciones diferenciales
fg=@(t,x)[x(2);
      (2*m*r^2*9.8*cos(x(3))*sin(x(3))/R^2+m*r*x(4)^2*sin(x(3)))
/(2*M+m-2*m*r^2*cos(x(3))^2/R^2); 
    x(4);
 (-m*r^2*x(4)^2*cos(x(3))*sin(x(3))/(2*M+m)-9.8*r*sin(x(3)))
/(R^2/2-m*r^2^cos(x(3))^2/(2*M+m))];
[t,x]=ode45(fg,[0,2],x0);
hold on
plot(t, x(:,2)) %velocidad dx/dt
%aproximación
v=@(t) m*r*u*(1-cos(Omega*t))/(2*M+m);
fplot(v,[0,2])
hold off
legend('numérico','aproximada','location','northwest')
grid on
xlabel('t')
ylabel('dx/dt')
title('Velocidad en el plano horizontal')

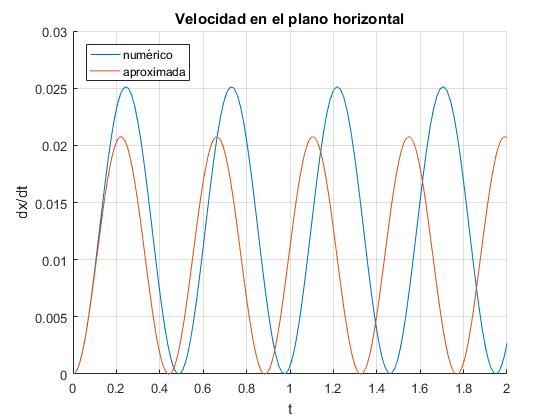
Como apreciamos, la botella medio llena de agua, se pone en movimiento, se vueve a parar y así, sucesivamente

En la imagen apreciamos la diferencia entre la solución del sistema de ecuaciones diferenciales (etiqueta numérico) y la aproximación para ángulos pequeños (etiqueta aproximada)

Comprobamos que el procedimiento numérico funciona adecuadamente, calculando la energía total T+V del sistema en cada instante t, que debe permanecer constante

${\displaystyle $ E=\frac{1}{2}(2M+m){\left(\frac{dx}{dt}\right)}^2+mr\frac{dx}{dt}\frac{d\theta }{dt}\cos \theta +\frac{1}{4}m{R}^2{\left(\frac{d\theta }{dt}\right)}^2-mgr\cos \theta $}$

>> E=(2*M+m)*x(:,2).^2/2+m*r*x(:,2).*x(:,4).*cos(x(:,3))
+m*R^2*x(:,4).^2/4-m*9.8*r*cos(x(:,3))
E =
   -0.3608
   -0.3608
   -0.3608
   ......   

Actividades

Se introduce

• El cociente entre la masa de agua y la masa del cilindro hueco m/M, en el control titulado Masa agua/botella
• El radio R en cm del cilindro hueco, en el control titulado Radio
• Las condiciones iniciales en el instante t=0. La velocidad inicial (dx/dt)₀ en el control titulado Velocidad inicial
• La velocidad angular inicial (dθ/dt)₀ en el control titulado Velocidad angular inicial

Se pulsa el botón titulado Nuevo

Se observa el movimiento del cilindro hueco y del agua en su interior (en color azul claro)

Se representa la velocidad del centro del cilindro hueco dx/dt en función del tiempo

Se resuelve el sistema de dos ecuaciones diferenciales por el procedimiento de Runge-Kutta, se calcula la energía del sistema en cada instante y se compara con la energía inicial. Si el procedimiento numérico funciona adecuadamente, el tanto por ciento de error será cero o próximo a cero.

${\displaystyle \left|\frac{E-E_0}{E_0}\right|·100}$

donde E es la energía del sistema en cualquier instante t, y E₀ es la energía inicial del sistema.

Movimiento de la botella medio llena en el plano inclinado

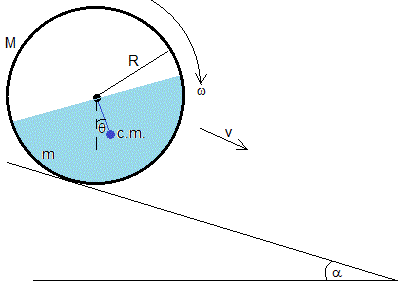
Consideremos ahora el caso de que la botella medio llena de agua se sitúa sobre un plano inclinado de ángulo pequeño α. Supongamos que el cilindro hueco rueda sin deslizar de modo que v=ωR

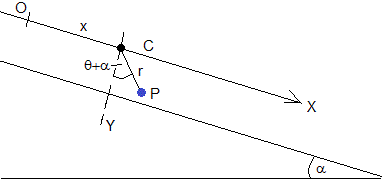
Establecemos los ejes tal como se muestra en la figura, el eje X a lo largo del plano inclinado y el eje Y perpendicular al dicho plano

En un instante dado, la posición del centro del cilindro C es x, y=0. La posición del centro de masas del agua P es

x_P=x+rsin(α+θ)
y_P=rcos(α+θ)

Derivamos con respecto del tiempo para obtener la velocidad.

${\displaystyle \begin{array}{l}\frac{d{x}_p}{dt}=\frac{dx}{dt}+r\cos (\alpha +\theta )\frac{d\theta }{dt}\\ \frac{d{y}_p}{dt}=-r\sin (\alpha +\theta )\frac{d\theta }{dt}\end{array}}$

Energía cinética

Ya hemos demostrado que la energía cinética de un cilindro hueco de masa M y radio R que rueda sin deslizar con velocidad dx/dt es

${\displaystyle M{\left(\frac{dx}{dt}\right)}^2}$

La energía cinética del agua se compone de dos términos. La energía cinética del centro de masas

${\displaystyle \frac{1}{2}m\left({\left(\frac{d{x}_p}{dt}\right)}^2+{\left(\frac{d{y}_p}{dt}\right)}^2\right)=\frac{1}{2}m\left({\left(\frac{dx}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2+2r\frac{dx}{dt}\frac{d\theta }{dt}\cos (\alpha +\theta )\right)}$

y la energía cinética de rotación alrededor de un eje paralelo al eje de simetría que pasa por el centro de masas con velocidad angular dθ/dt

${\displaystyle \frac{1}{2}{I}_{cm}{\left(\frac{d\theta }{dt}\right)}^2}$

La energía cinética total es

${\displaystyle \begin{array}{l}T=M{\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}m\left({\left(\frac{dx}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2+2r\frac{dx}{dt}\frac{d\theta }{dt}\cos (\alpha +\theta )\right)+\frac{1}{2}{I}_{cm}{\left(\frac{d\theta }{dt}\right)}^2=\\ \frac{1}{2}(2M+m){\left(\frac{dx}{dt}\right)}^2+mr\frac{dx}{dt}\frac{d\theta }{dt}\cos (\alpha +\theta )+\frac{1}{4}m{R}^2{\left(\frac{d\theta }{dt}\right)}^2\end{array}}$

Energía potencial

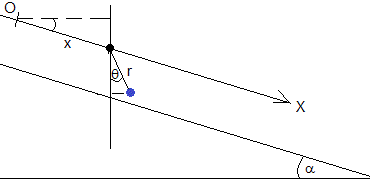
Tomando como origen el punto O, la energía potencial del centro del cilindro es -Mgxsinα, y la del centro de masas del agua, -mg(xsinα+rcosθ). En total

${\displaystyle V=-(M+m)gx\sin \alpha -mgr\cos \theta }$

Ecuaciones del movimiento

La lagrangiana de este sistema es

${\displaystyle \begin{array}{l}L=T-V=\frac{1}{2}(2M+m){\left(\frac{dx}{dt}\right)}^2+mr\frac{dx}{dt}\frac{d\theta }{dt}\cos (\alpha +\theta )+\frac{1}{4}m{R}^2{\left(\frac{d\theta }{dt}\right)}^2\\ +(M+m)gx\sin \alpha +mgr\cos \theta \end{array}}$

Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right)-\frac{\partial L}{\partial x}=0\\ (2M+m)\frac{d^{2}x}{d{t}^2}+mr\frac{d^2\theta }{d{t}^2}\cos (\alpha +\theta )-mr{\left(\frac{d\theta }{dt}\right)}^2\sin (\alpha +\theta )-(M+m)g\sin \alpha =0\\ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \frac{1}{2}{R}^2\frac{d^2\theta }{d{t}^2}+r\frac{d^{2}x}{d{t}^2}\cos (\alpha +\theta )+gr\sin \theta =0\end{array}}$

En este sistema de dos ecuaciones despejamos las derivadas segundas, respecto del tiempo

${\displaystyle \begin{array}{l}\left(2M+m-\frac{2m{r}^2}{R^2}{\cos }^2(\alpha +\theta )\right)\frac{d^{2}x}{d{t}^2}-\frac{2mg{r}^2}{R^2}\sin \theta \cos (\alpha +\theta )-\\ mr{\left(\frac{d\theta }{dt}\right)}^2\sin (\alpha +\theta )-(M+m)g\sin \alpha =0\\ \left(\frac{1}{2}{R}^2-\frac{m{r}^2}{2M+m}{\cos }^2(\alpha +\theta )\right)\frac{d^2\theta }{d{t}^2}+\frac{m{r}^2}{2M+m}{\left(\frac{d\theta }{dt}\right)}^2\sin (\alpha +\theta )\cos (\alpha +\theta )+\\ \frac{(M+m)g}{2M+m}r\sin \alpha \cos (\alpha +\theta )+gr\sin \theta =0\end{array}}$

Aproximaciones

Si θ, α y dθ/dt son pequeños, hacemos las siguientes aproximaciones: cos(α+θ)≈1, sinθ≈θ, sinα≈α, (dθ/dt)²sin(α+θ)≈0. El sistema de dos ecuaciones se reduce a

${\displaystyle \begin{array}{l}\left(2M+m-\frac{2m{r}^2}{R^2}\right)\frac{d^{2}x}{d{t}^2}-\frac{2mg{r}^2}{R^2}\theta -(M+m)g\alpha =0\\ \left(\frac{1}{2}{R}^2-\frac{m{r}^2}{2M+m}\right)\frac{d^2\theta }{d{t}^2}+\frac{(M+m)g}{2M+m}r\alpha +gr\theta =0\end{array}}$

La segunda ecuación diferencial es conocida, se trata de un Movimiento Armónico Simple, de frecuencia angular Ω

${\displaystyle \begin{array}{l}\frac{d^2\theta }{d{t}^2}+{\Omega }^2\theta =-kk={\Omega }^2\alpha \frac{m+M}{2M+m}{\Omega }^2=\frac{2(2M+m)r}{(2M+m)R^2-2m{r}^2}g\\ \theta =A\sin (\Omega t)+B\cos (\Omega t)-\frac{k}{{\Omega }^2}\end{array}}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales. En el instante t=0, θ=0, y dθ/dt=0

${\displaystyle \begin{array}{l}\theta =-\frac{k}{{\Omega }^2}\left(1-\cos (\Omega t)\right)\\ \theta =-\alpha \frac{m+M}{2M+m}\left(1-\cos (\Omega t)\right)\end{array}}$

Conocida la solución de la segunda ecuación diferencial, θ(t), buscamos una solución de la primera x(t) que es la posición del centro de la botella

${\displaystyle \begin{array}{l}\left(2M+m-\frac{2m{r}^2}{R^2}\right)\frac{d^{2}x}{d{t}^2}+\frac{2mg{r}^2}{R^2}\alpha \frac{m+M}{2M+m}\left(1-\cos (\Omega t)\right)-(M+m)g\alpha =0\\ \frac{d^{2}x}{d{t}^2}=\frac{(M+m)g\alpha }{2M+m}+\frac{mrk}{2M+m}\cos (\Omega t)\end{array}}$

Integramos la ecuación diferencial, para obtener la velocidad del centro de la botella, dx/dt, sabiendo que en instante t=0, parte del reposo, dx/dt=0

${\displaystyle \frac{dx}{dt}=\frac{M+m}{2M+m}\alpha gt+r\alpha \frac{m(m+M)}{{\left(2M+m\right)}^2}\Omega \sin (\Omega t)}$

Ejemplo

Sea el radio del cilindro hueco R=44 mm, su masa M=0.14 kg, la masa de agua m=0.51 kg, el ángulo del plano inclinado α=15°. La posición del centro de masas del agua es r=4R/(3π)

Integramos el sistema de dos ecuaciones diferenciales, con las condiciones iniciales t=0, θ=0, dθ/dt=0. El centro del cilindro hueco parte del origen en reposo, x=0, dx/dt=0

Elaboramos un script para repesentar la velocidad dx/dt del centro del cilindro hueco en función del tiempo t y compararlos con la aproximación para ángulos pequeños

R=44/1000; %radio de la botella
M=0.14; %masa botella
m=0.51; %masa del agua
alfa=pi/12; %ángulo del plano inclinado

r=4*R/(3*pi); %posición del c.m. del agua
Omega=sqrt(2*(2*M+m)*r*9.8/((2*M+m)*R^2-2*m*r^2)); %frecuencia angular
x0=[0,0,0,0];
%sistema de dos ecuaciones diferenciales
fg=@(t,x)[x(2);
      (2*m*r^2*9.8*sin(x(3))*cos(alfa+x(3))/R^2+m*r*x(4)^2*sin(alfa+x(3))+
(m+M)*9.8*sin(alfa))/(2*M+m-2*m*r^2*cos(alfa+x(3))^2/R^2); 
    x(4);
 (-m*r^2*x(4)^2*cos(alfa+x(3))*sin(alfa+x(3))/(2*M+m)-(M+m)*r*9.8*sin(alfa)*
cos(alfa+x(3))/(2*M+m)-9.8*r*sin(x(3)))/
(R^2/2-m*r^2*cos(alfa+x(3))^2/(2*M+m))];
[t,x]=ode45(fg,[0,2],x0);
hold on
plot(t, x(:,2)) %velocidad dx/dt
%aproximación
v=@(t) (M+m)*alfa*9.8*t/(2*M+m)+m*(M+m)*Omega*r*alfa*sin(Omega*t)/(2*M+m)^2;
fplot(v,[0,2])
hold off
legend('numérico','aproximada','location','northwest')
grid on
xlabel('t')
ylabel('dx/dt')
title('Velocidad en el plano inclinado')

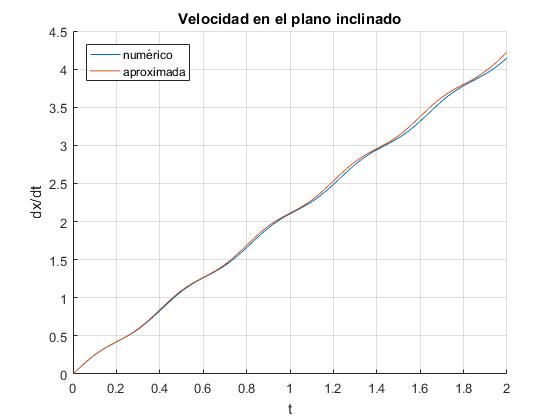
En la imagen, apreciamos la diferencia entre la solución del sistema de ecuaciones diferenciales (etiqueta numérico) y la aproximación para ángulos pequeños (etiqueta aproximada)

Comprobamos que el procedimiento numérico funciona adecuadamente, calculando la energía total T+V del sistema en cada instante t, que debe permanecer constante

${\displaystyle \begin{array}{l}E=\frac{1}{2}(2M+m){\left(\frac{dx}{dt}\right)}^2+mr\frac{dx}{dt}\frac{d\theta }{dt}\cos (\alpha +\theta )+\frac{1}{4}m{R}^2{\left(\frac{d\theta }{dt}\right)}^2\\ -(M+m)gx\sin \alpha -mgr\cos \theta \end{array}}$

>> E=(2*M+m)*x(:,2).^2/2+m*r*x(:,2).*x(:,4).*cos(alfa+x(:,3))
+m*R^2*x(:,4).^2/4-(M+m)*9.8*x(:,1)*sin(alfa)-m*9.8*r*cos(x(:,3))
E =
   -0.0933
   -0.0933
   -0.0933
   ......   

Actividades

Se introduce

• El cociente entre la masa de agua y la masa del cilindro hueco m/M, en el control titulado Masa agua/botella
• El radio R en cm del cilindro hueco, en el control titulado Radio
• El ángulo del plano inclinado en grados, en el control titulado Plano inclinado

Se pulsa el botón titulado Nuevo

Se han establecido las condiciones iniciales en el instante t=0: la posición x=0, θ=0, y la velocidad dx/dt=0, dθ/dt=0

Se observa el movimiento del cilindro hueco y del agua en su interior (en color azul claro)

Se representa la velocidad del centro del cilindro hueco dx/dt en función del tiempo

Se resuelve el sistema de dos ecuaciones diferenciales por el procedimiento de Runge-Kutta, se calcula la energía del sistema en cada instante y se compara con la energía inicial. Si el procedimiento numérico funciona adecuadamente, el tanto por ciento de error será cero o próximo a cero.

Referencias

Andréane Bourges, Amélie Chardac, Aude Caussarieu, Nicolas Plihon, Nicolas Taberlet. Oscillations in a half-empty bottle. Am. J. Phys. 86 (2) February 2018, pp.119-125