Partícula que desliza sobre la superficie interior de un tubo que rueda sobre un plano horizontal

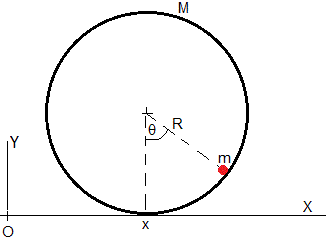
Consideremos un tubo de pequeño espesor, de masa M y radio R que rueda sin deslizar sobre un plano horizontal. Una partícula de masa m puede deslizar sin rozamiento sobre la superficie interior del tubo. Vamos a estudiar el movimiento de este sistema.

La energía cinética del tubo es la suma de la energía cinética de traslación del centro de masas con velocidad v_c y de rotación alrededor de un eje que pasa por el centro de masas con velocidad angular ω. Ambas velocidades están relacionadas, v_c=ω·R.

El momento de inercia de un tubo de pequeño espesor, de masa M y radio R es, MR²

${\displaystyle E_{k1}=\frac{1}{2}M{v}_c^2+\frac{1}{2}\left(M{R}^2\right){\omega }^2=M{v}_c^2=M{\left(\frac{dx}{dt}\right)}^2}$

Siendo x la posición del centro de masas del tubo en el instante t. Como el tubo se mueve en el plano horizontal, su energía potencial no cambia

La posición y velocidad de la partícula de masa m es

${\displaystyle \overrightarrow{r}\{\begin{array}{l}{x}_p=x+r\sin \theta \\ y_p=R-R\cos \theta \end{array}\overrightarrow{v}\{\begin{array}{l}\frac{d{x}_p}{dt}=\frac{dx}{dt}+R\cos \theta \frac{d\theta }{dt}\\ \frac{d{y}_p}{dt}=R\sin \theta \frac{d\theta }{dt}\end{array}}$

La energía cinética de la partícula es

${\displaystyle E_{k2}=\frac{1}{2}m\left\{{\left(\frac{d{x}_p}{dt}\right)}^2+{\left(\frac{d{y}_p}{dt}\right)}^2\right\}=\frac{1}{2}m\left\{{\left(\frac{dx}{dt}\right)}^2+R^2{\left(\frac{d\theta }{dt}\right)}^2+2R\cos \theta \frac{dx}{dt}\frac{d\theta }{dt}\right\}}$

La energía potencial es, E_p=mgR(1-cosθ)

La lagrangiana L=E_k1+E_k1-E_p

${\displaystyle L=\left(M+\frac{1}{2}m\right){\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}m{R}^2{\left(\frac{d\theta }{dt}\right)}^2+mR\cos \theta \frac{dx}{dt}\frac{d\theta }{dt}-mgR(1-\cos \theta )}$

• Como L no depende de x tenemos una constante del movimiento, que denominamos P

${\displaystyle \begin{array}{l}\frac{\partial L}{\partial \dot{x}}=\text{cte}\\ \left(2M+m\right)\frac{dx}{dt}+mR\cos \theta \frac{d\theta }{dt}=P\end{array}}$

Integramos la ecuación diferencial

${\displaystyle x=\frac{1}{2M+m}\left(Pt-mR\sin \theta +mR\sin {\theta }_0\right)}$

Supondremos que el tubo parte del origen, x=0, en el instante t=0

• La energía se mantiene constante

${\displaystyle \begin{array}{l}E=\left(M+\frac{1}{2}m\right){\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}m{R}^2{\left(\frac{d\theta }{dt}\right)}^2+mR\cos \theta \frac{dx}{dt}\frac{d\theta }{dt}+mgR(1-\cos \theta )\\ E=\frac{1}{2}\frac{P^2}{2M+m}+\frac{1}{2}m{R}^2\left(\frac{m{\sin }^2\theta +2M}{2M+m}\right){\left(\frac{d\theta }{dt}\right)}^2+mgR(1-\cos \theta )\end{array}}$

• Para obtener la otra ecuación del movimiento, expresamos la lagrangiana L en términos de θ como se ha hecho para la energía

${\displaystyle \begin{array}{l}L=\frac{1}{2}\frac{P^2}{2M+m}+\frac{1}{2}m{R}^2\left(\frac{m{\sin }^2\theta +2M}{2M+m}\right){\left(\frac{d\theta }{dt}\right)}^2-mgR(1-\cos \theta )\\ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \frac{2M+m{\sin }^2\theta }{2M+m}\frac{d^2\theta }{d{t}^2}+\frac{m}{2M+m}\sin \theta \cos \theta {\left(\frac{d\theta }{dt}\right)}^2+\frac{g}{R}\sin \theta =0\end{array}}$

Para determinar la posición θ de la partícula en función del tiempo t, resolvemos la ecuación diferencial, con las siguientes condiciones iniciales: en el instante t=0, x=0, dx/dt=0 (el tubo parte origen en reposo) y para la partícula: θ=θ₀, dθ/dt=(dθ/dt)₀

La constante del movimiento P vale

${\displaystyle P=mR\cos {\theta }_0{\left(\frac{d\theta }{dt}\right)}_0}$

Ejemplo

• Radio del tubo, R=1
• Masa del tubo, M=1
• Masa de la partícula, m=2
• El tubo parte del reposo en el origen
• La partícula se desvía θ₀=π/6 de su posición de equilibrio y se suelta, (dθ/dt)₀=0

R=1; %radio del tubo
M=1; %masa del tubo
m=2; %masa de la partícula
th_0=pi/6; %posición angular inicial partícula
wP=0;  %velocidad angular inicial partícula
P=m*R*cos(th_0)*wP; 
x0=[th_0,wP];
f=@(t,x) [x(2); -(9.8*(2*M+m)/R+m*cos(x(1))*x(2)^2)*sin(x(1))/
(2*M+m*sin(x(1))^2)]; 
[t,x]=ode45(f,[0,5],x0);
xTubo=(P*t-m*R*sin(x(:,1))+m*R*sin(th_0))/(2*M+m);
hold on
plot(t,x(:,1),'r') %partícula
plot(t,xTubo,'b') %tubo
hold off
grid on
xlabel('t')
ylabel('\theta,x')
title('Movimiento de la partícula y tubo')
%energía
E=P^2/(4*M+2*m)+m*R^2*(m*sin(x(:,1)).^2+2*M).*x(:,2).^2/
(4*M+2*m)+m*9.8*R*(1-cos(x(:,1)));

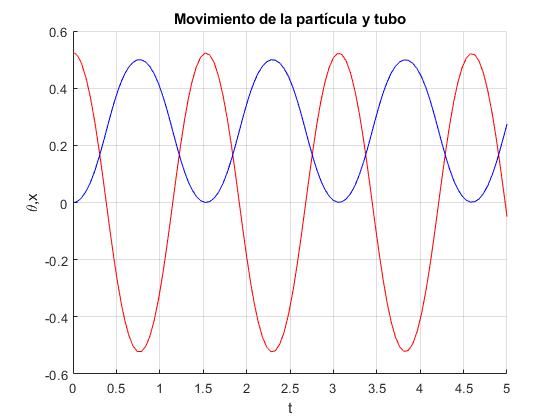
En azul, la posición angular θ de la partícula, en rojo, la posición del eje del tubo, x

Comprobamos que la energía inicial, es aproximadamente igual a la energía en cada instante

>> E0=P^2/(4*M+2*m)+m*R^2*(m*sin(th_0)^2+2*M)*wP^2/
(4*M+2*m)+m*9.8*R*(1-cos(th_0))
E0 =    2.6259
>> E=P^2/(4*M+2*m)+m*R^2*(m*sin(x(:,1)).^2+2*M).*x(:,2).^2/
(4*M+2*m)+m*9.8*R*(1-cos(x(:,1)))
E = 2.6259
    ...
    2.5702
    2.5695

Cambiamos en el script las condiciones iniciales

• La partícula se mantiene en la posición de equilibrio, θ₀=0 y se le proporciona una velocidad angular, (dθ/dt)₀=0.2

....
th_0=0; %posición angular inicial partícula
wP=0.2;  %velocidad angular inicial partícula
....

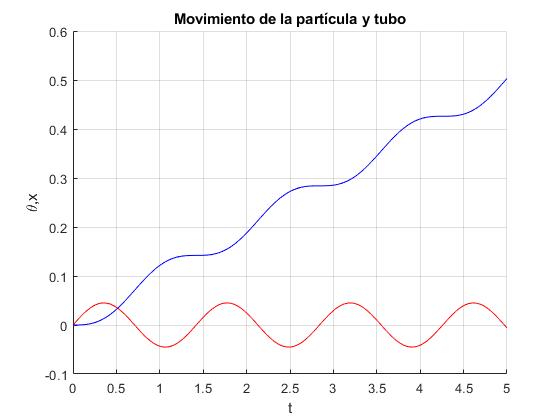
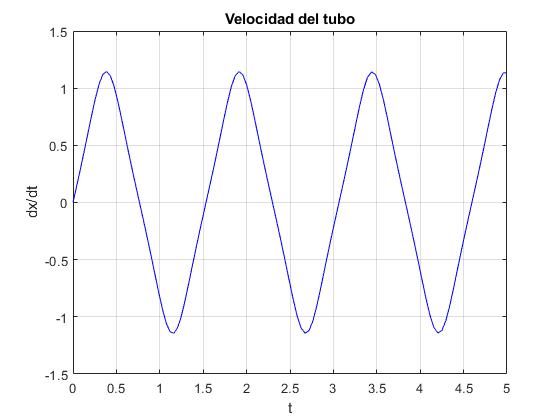
Representamos la velocidad dx/dt del tubo en función del tiempo, observamos los instantes en los que se detiene. La diferencia de dos tiempos consecutivos es un periodo, aproximadamente 1.52 s. Se puede comparar esta medida con el periodo calculado mediante las aproximación de pequeña amplitud (en el apartado que viene a continuación)

R=1; %radio del tubo
M=1; %masa del tubo
m=2; %masa de la partícula
th_0=pi/6; %posición angular inicial partícula
wP=0;  %velocidad angular inicial partícula
P=m*R*cos(th_0)*wP; 
x0=[th_0,wP];
f=@(t,x) [x(2); -(9.8*(2*M+m)/R+m*cos(x(1))*x(2)^2)*sin(x(1))/
(2*M+m*sin(x(1))^2)]; 
[t,x]=ode45(f,[0,5],x0);
vTubo=(P-m*R*cos(x(:,1)).*x(:,2))/(2*M+m);
plot(t,vTubo,'b') %tubo
grid on
xlabel('t')
ylabel('dx/dt')
title('Velocidad del tubo')

Aproximaciones

Cuando θ es pequeño sinθ≈θ, cosθ=1, θ(dθ/dt)²≈0

La ecuación diferencial en θ se transforma en

${\displaystyle \begin{array}{l}\frac{2M}{2M+m}\frac{d^2\theta }{d{t}^2}+\frac{g}{R}\theta =0\\ {\omega }^2=\frac{g}{R}\frac{2M+m}{2M}\end{array}}$

>> w2=9.8*(2*M+m)/(R*2*M)
w2 =   19.6000
>> 2*pi/sqrt(w2)
ans =    1.4192

Que es la ecuación de un Movimiento Armónico Simple de frecuencia angular o periodo P=2π/ω

Actividades

Se introduce

• La masa m de la partícula, en el control titulado Masa partícula
• La posición angular inicial de la partícula θ₀, en el control titulado Posición
• La velocidad angular inicial de la partícula (dθ/dt)₀, en el control titulado Velocidad angular

Se ha fijado

• La masa M=1 y el radio R=1, del tubo que rueda sobre el plano horizontal
• La posición inicial y velocidad inicial del tubo, parte del origen en reposo

Se pulsa el botón titulado Nuevo

Se muestra el tubo de masa M y radio r rodando en el plano horizontal y la partícula de masa m deslizando en su superficie interior

Se proporcionan los datos

• Tiempo t
• La posición x y velocidad dx/dt del centro del tubo
• La posición angular θ y la velocidad angular dθ/dt de la partícula

Se sugiere probar estos dos ejemplos, observando las diferencias

• Posicición inicial θ₀=30°, velocidad angular inicial (dθ/dt)₀=0
• Posicición inicial θ₀=0, velocidad angular inicial (dθ/dt)₀=0.4

El lector puede medir el periodo de la oscilación utilizando los botones Pausa || y Paso a paso >|

El programa calcula en cada instante el tanto por ciento de error relativo en la energía o el cociente

${\displaystyle \left|\frac{E-E_0}{E_0}\right|·100}$

donde E es la energía del sistema en cualquier instante t, y E₀ es la energía inicial del sistema.

Este valor se proporciona en caracteres de color rojo en la parte izquierda. Su valor debe ser siempre cero, o un valor muy pequeño lo que indica que la energía del sistema permanece constante y el programa realiza los cálculos correctamente.

Cilindro macizo que rueda dentro de un tubo que rueda sobre un plano horizontal

Superficie cilíndrica fija

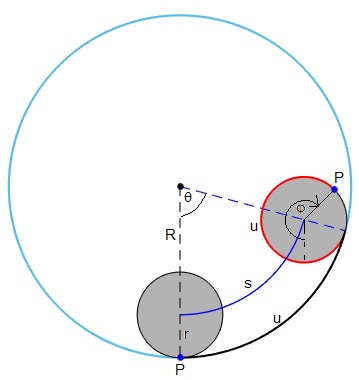
Un cuerpo cilíndrico de radio r rueda sin deslizar sobre la superficie interior de un tubo radio R. El centro del cuerpo describe un arco s=(R-r)θ (en color azul), mientras el cuerpo rueda una longitud u=Rθ sobre la pista (en color negro) e igual al arco de color rojo pintado sobre el cuerpo

En la figura, se señala la posición inicial del punto P del cuerpo y su posición angular en el instante t, φ=u/r-θ=Rθ/r-θ

Parte de la figura ha sido elaborada con el siguiente código

th=75*pi/180; %ángulo
r=0.25; %radio del cuerpo que rueda
hold on
%pista
fplot(@(t) cos(t), @(t) sin(t), [0,2*pi], 'linewidth',1.5)
%cuerpo
ang=(1:360)*pi/180;
x1=r*cos(ang);
y1=-(1-r)+r*sin(ang);
fill(x1,y1,[0.7 0.7 0.7])
line([0,0],[0,-1],'linestyle','--')
plot(0,0,'bo','linewidth',1,'markersize',4,'markeredgecolor','k',
'markerfacecolor','k')

x1=(1-r)*sin(th)+r*cos(ang);
y1=-(1-r)*cos(th)+r*sin(ang);
fill(x1,y1,[0.7 0.7 0.7])
line([0,sin(th)],[0,-cos(th)],'linestyle','--','color','b')
fplot(@(t) (1-r)*sin(th)+r*cos(t), @(t) -(1-r)*cos(th)+r*sin(t), 
[-th/r-(pi/2-th),-(pi/2-th)], 'linewidth',1.5, 'color','r')
fplot(@(t) (1-r)*cos(t), @(t) (1-r)*sin(t), [-pi/2,-(pi/2-th)], 
'linewidth',1,'color','b')
fplot(@(t) cos(t), @(t) sin(t), [-pi/2,-(pi/2-th)], 'linewidth',1.5,
'color','k')
plot(0,-1,'bo','linewidth',1,'markersize',4,'markeredgecolor','b',
'markerfacecolor','b')
plot((1-r)*sin(th)+r*cos(-th/r-(pi/2-th)),-(1-r)*cos(th)+r*sin(-th/r-(pi/2-
th)),'bo','linewidth',1,'markersize',4,'markeredgecolor','b',
'markerfacecolor','b')
plot(0,0,'bo','linewidth',1,'markersize',4,'markeredgecolor','k',
'markerfacecolor','k')
line([0,0],[0,-1],'linestyle','--','color','k')

hold off
axis equal
axis off

Superficie cilíndrica móvil

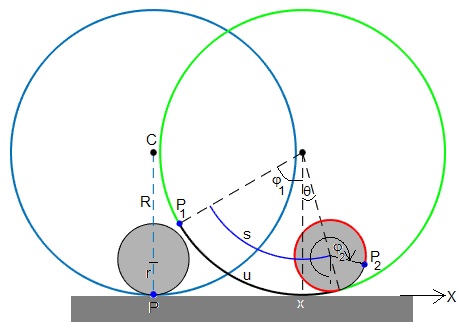
La superficie cilíndrica de radio R, rueda sin deslizar sobre el plano horizontal, en un tiempo t, su centro C se desplaza x y gira alrededor de un eje que pasa por su centro un ángulo φ₁=x/R, el punto P de la superficie cilíndrica se convierte en el punto P₁. Un cilindro macizo de radio r rueda sin deslizar sobre la superficie cilíndrica interior de radio R. En el instante t=0, el cilindro está situado en el origen, tal como se indica en la parte izquierda de la figura.

El centro del cilindro macizo se ha desplazado un arco s (en color azul), el cilindro macizo se ha desplazado un arco u rodando sobre la superficie cilíndica. La posición angular θ del centro del cilindro macizo, medida desde el origen, θ=u/R-φ₁ o bien, u=R(θ+φ₁).

El punto de contacto P sobre la superficie del cilindro macizo se ha convertido en el punto P₂, ha girado un ángulo u/r, su posición angular es φ₂=u/r-θ.

${\displaystyle {\phi }_2=\frac{R(\theta +{\phi }_1)}{r}-\theta =\frac{R-r}{r}\theta +\frac{R}{r}{\phi }_1}$

Parte de la figura ha sido elaborada con el siguiente código

th=75*pi/180; %ángulo
r=0.25; %radio del cuerpo que rueda
hold on
%pista
fplot(@(t) cos(t), @(t) sin(t), [0,2*pi], 'linewidth',1.5)
%cuerpo
ang=(1:360)*pi/180;
x1=r*cos(ang);
y1=-(1-r)+r*sin(ang);
fill(x1,y1,[0.7 0.7 0.7])
line([0,0],[0,-1],'linestyle','--')
plot(0,0,'bo','linewidth',1,'markersize',4,'markeredgecolor','k',
'markerfacecolor','k')
plot(0,-1,'bo','linewidth',1,'markersize',4,'markeredgecolor','b',
'markerfacecolor','b')

%pista
aGira=pi/3;
fplot(@(t) aGira+cos(t), @(t) sin(t), [0,2*pi], 'linewidth',1.5,'color','g')

x1=aGira+(1-r)*sin(th-aGira)+r*cos(ang);
y1=-(1-r)*cos(th-aGira)+r*sin(ang);
fill(x1,y1,[0.7 0.7 0.7])
line([aGira,aGira+sin(th-aGira)],[0,-cos(th-aGira)],'linestyle','--',
'color','k')
fplot(@(t) aGira+cos(t), @(t) sin(t), [-pi/2-aGira,-(pi/2-th+aGira)], 
'linewidth',1.5,'color','k')
fplot(@(t) aGira+(1-r)*sin(th-aGira)+r*cos(t), @(t) -(1-r)*cos(th-aGira)+r*sin(t),
 [-th/r-(pi/2-th+aGira),-(pi/2-th+aGira)], 'linewidth',1.5, 'color','r')
fplot(@(t) aGira+(1-r)*cos(t), @(t) (1-r)*sin(t), [-pi/2-aGira,-(pi/2-th+aGira)],
 'linewidth',1,'color','b')
plot(aGira-sin(aGira),-cos(aGira),'bo','markersize',4,'markeredgecolor','b',
'markerfacecolor','b')
plot(aGira+(1-r)*sin(th-aGira)+r*cos(-th/r-(pi/2-th+aGira)),-(1-r)*cos(th-aGira)+
r*sin(-th/r-(pi/2-th+aGira)),'bo','markersize',4,'markeredgecolor','b',
'markerfacecolor','b')
plot(aGira,0,'bo','linewidth',1,'markersize',4,'markeredgecolor','k',
'markerfacecolor','k')
line([aGira,aGira],[0,-1],'linestyle','--','color','k')
line([aGira,aGira-sin(aGira)],[0,-cos(aGira)],'linestyle','--',
'color','k')

hold off
axis equal
axis off

Posición y velocidad del centro del cilindro macizo

La posición del centro del cilindro macizo y las componentes de su velocidad son

${\displaystyle \{\begin{array}{l}{x}_2=x+(R-r)\sin \theta \\ y_2=R-(R-r)\cos \theta \end{array}\{\begin{array}{l}\frac{d{x}_2}{dt}=\frac{dx}{dt}+(R-r)\cos \theta \frac{d\theta }{dt}\\ \frac{d{y}_2}{dt}=(R-r)\sin \theta \frac{d\theta }{dt}\end{array}}$

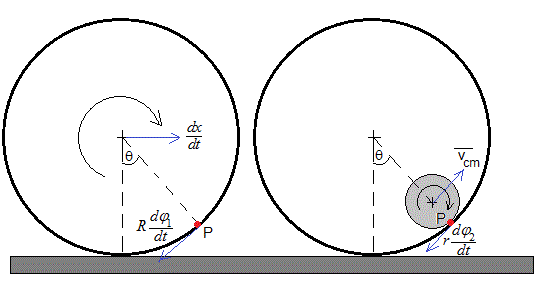
Calculamos la velocidad del punto P de contacto entre el cilindro macizo y el tubo.

En la figura de la izquierda, la velocidad del punto P situado en la posición angular θ en la superficie interior del tubo de radio R, es la suma de la velocidad de traslación del c.m. dx/dt y de rotación alrededor de un eje que pasa por el centro Rdφ₁/dt. Sus componentes son

${\displaystyle \{\begin{array}{l}\frac{dx}{dt}-R\frac{d{\phi }_1}{dt}\cos \theta =R\frac{d{\phi }_1}{dt}-R\frac{d{\phi }_1}{dt}\cos \theta \\ -R\frac{d{\phi }_1}{dt}\sin \theta \end{array}}$

En la figura de la derecha, la velocidad del punto de contacto P sobre la superficie del cilindro macizo es la suma de la velocidad de su centro, cuyas componentes ya hemos calculado y la velocidad de rotación alrededor de un eje que pasa por el centro del cilindro macizo rdφ₂/dt. Las componentes son

${\displaystyle \{\begin{array}{l}\frac{dx}{dt}+(R-r)\cos \theta \frac{d\theta }{dt}-r\frac{d{\phi }_2}{dt}\cos \theta \\ (R-r)\sin \theta \frac{d\theta }{dt}-r\frac{d{\phi }_2}{dt}\sin \theta \end{array}}$

Teniendo en cuenta la relación entre φ₂, θ y φ₁ establecida en el apartado anterior

${\displaystyle \{\begin{array}{l}R\frac{d{\phi }_1}{dt}+(R-r)\cos \theta \frac{d\theta }{dt}-(R-r)\frac{d\theta }{dt}\cos \theta -R\frac{d{\phi }_1}{dt}\cos \theta =R\frac{d{\phi }_1}{dt}-R\frac{d{\phi }_1}{dt}\cos \theta \\ (R-r)\sin \theta \frac{d\theta }{dt}-(R-r)\frac{d\theta }{dt}\sin \theta -R\frac{d{\phi }_1}{dt}\sin \theta =-R\frac{d{\phi }_1}{dt}\sin \theta \end{array}}$

El punto P está en reposo en el sistema de referencia que se mueve con el tubo. Que es la condición para que el cilindro macizo ruede sin deslizar sobre la superficie interior del tubo

Energía del sistema

• La energía potencial del centro del cilindro macizo de masa m y radio r es

E_p=mg(R-(R-r)cosθ)

• La energía cinética del tubo cilíndrico de masa M y radio R es

${\displaystyle E_{k1}=\frac{1}{2}M{\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}\left(M{R}^2\right){\left(\frac{d{\phi }_1}{dt}\right)}^2=M{\left(\frac{dx}{dt}\right)}^2}$

• La energía cinética del cilindro macizo de masa m y radio r es

${\displaystyle \begin{array}{l}{E}_{k2}=\frac{1}{2}m\left\{{\left(\frac{d{x}_2}{dt}\right)}^2+{\left(\frac{d{y}_2}{dt}\right)}^2\right\}+\frac{1}{2}\left(\frac{1}{2}m{r}^2\right){\left(\frac{d{\phi }_2}{dt}\right)}^2=\\ \frac{1}{2}m{\left(\frac{dx}{dt}\right)}^2+\frac{3}{4}m{\left(R-r\right)}^2{\left(\frac{d\theta }{dt}\right)}^2+m(R-r)\cos \theta \frac{dx}{dt}\frac{d\theta }{dt}+\frac{1}{4}m{\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}m(R-r)\frac{d\theta }{dt}\frac{dx}{dt}=\\ \frac{3}{4}m{\left(R-r\right)}^2{\left(\frac{d\theta }{dt}\right)}^2+\frac{3}{4}m{\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}m(R-r)\left(2\cos \theta +1\right)\frac{d\theta }{dt}\frac{dx}{dt}\end{array}}$

La energía total en cada instante t se conserva y es igual a la energía inicial

${\displaystyle E=\frac{3}{4}m{\left(R-r\right)}^2{\left(\frac{d\theta }{dt}\right)}^2+\left(\frac{3}{4}m+M\right){\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}m(R-r)\left(2\cos \theta +1\right)\frac{d\theta }{dt}\frac{dx}{dt}+mg\left(R-(R-r)\cos \theta \right)}$

Ecuaciones del movimiento

La lagrangiana, L=E_k1+E_k2-E_p es

${\displaystyle L=\frac{3}{4}m{\left(R-r\right)}^2{\left(\frac{d\theta }{dt}\right)}^2+\left(\frac{3}{4}m+M\right){\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}m(R-r)\left(2\cos \theta +1\right)\frac{d\theta }{dt}\frac{dx}{dt}-mg\left(R-(R-r)\cos \theta \right)}$

La lagrangiana L no depende de x, tenemos una constante del movimiento

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right)=0\frac{\partial L}{\partial \dot{x}}=\text{cte}\\ \left(\frac{3}{2}m+2M\right)\frac{dx}{dt}+\frac{1}{2}m(R-r)\left(2\cos \theta +1\right)\frac{d\theta }{dt}=v_0\left(\frac{3}{2}m+2M\right)\\ \frac{dx}{dt}=v_0-\frac{m(R-r)}{3m+4M}\left(2\cos \theta +1\right)\frac{d\theta }{dt}\end{array}}$

Integramos esta ecuación, con las condiciones iniciales: en el instante t=0, θ=θ₀, x=0, para obtener la posición x del centro del tubo en función del tiempo t y de la posición angular θ del centro del cilindro macizo

${\displaystyle \begin{array}{l}x=v_{0}t-\frac{m(R-r)}{3m+4M}{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\left(2\cos \theta +1\right)d\theta }\\ x=v_{0}t-\frac{m(R-r)}{3m+4M}\left(2\sin \theta +\theta -2\sin {\theta }_0-{\theta }_0\right)\end{array}}$

Expresamos la lagrangiana L en términos del ángulo θ

${\displaystyle \begin{array}{l}L=\frac{3}{4}m{\left(R-r\right)}^2{\left(\frac{d\theta }{dt}\right)}^2+\left(\frac{3}{4}m+M\right){\left\{v_0-\frac{m(R-r)}{3m+4M}\left(2\cos \theta +1\right)\frac{d\theta }{dt}\right\}}^2+\\ \frac{1}{2}m(R-r)\left(2\cos \theta +1\right)\frac{d\theta }{dt}\left\{v_0-\frac{m(R-r)}{3m+4M}\left(2\cos \theta +1\right)\frac{d\theta }{dt}\right\}-mg\left(R-(R-r)\cos \theta \right)\\ L=\frac{m{(R-r)}^2}{4}\left\{3-\frac{m}{3m+4M}{\left(2\cos \theta +1\right)}^2\right\}{\left(\frac{d\theta }{dt}\right)}^2+\left(\frac{3}{4}m+M\right)v_0^2-mg\left(R-(R-r)\cos \theta \right)\end{array}}$

La ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{d\dot{\theta }}\right)-\frac{\partial L}{d\theta }=0\\ \frac{1}{2}\left\{3\left(3m+4M\right)-m{\left(2\cos \theta +1\right)}^2\right\}\frac{d^2\theta }{d{t}^2}+m\left(2\cos \theta +1\right)\sin \theta {\left(\frac{d\theta }{dt}\right)}^2+\frac{\left(3m+4M\right)g}{R-r}\sin \theta =0\end{array}}$

Para determinar la posición θ del cilindro macizo en función del tiempo t, integramos la ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales: en el instante t=0, x=0, dx/dt=0 (el tubo parte del reposo en el origen) y para el cilindro macizo: θ=θ₀, dθ/dt=(dθ/dt)₀

La constante del movimiento v₀ vale

${\displaystyle v_0=\frac{m(R-r)}{3m+4M}\left(2\cos {\theta }_0+1\right){\left(\frac{d\theta }{dt}\right)}_0}$

Ejemplo

• Radio del tubo, R=1
• Masa del tubo, M=1
• Masa del cilindro macizo, m=2
• Radio del cilindro macizo, r=0.25
• El tubo parte del reposo en el origen
• El cilindro macizo se desvía θ₀=π/6 y se suelta, (dθ/dt)₀=0

R=1; %radio superficie cilíndrica
r=0.25; %radio cilindro macizo
M=1; %masa superficie cilíndrica
m=2; %masa cilindro macizo

wCilindro=0;  %velocidad angular inicial
th_0=pi/6; %posición angular inicial

v0=m*(R-r)*(2*cos(th_0)+1)*wCilindro/(3*m+4*M);
x0=[th_0,wCilindro];
f=@(t,x) [x(2); -2*(2*cos(x(1))+1)*sin(x(1))*m*x(2)^2/
(3*(3*m+4*M)-(2*cos(x(1))+1)^2*m)-2*9.8*sin(x(1))*(3*m+4*M)/((R-r)*(3*(3*m+4*M)-
(2*cos(x(1))+1)^2*m))]; 
[t,x]=ode45(f,[0,5],x0);
xTubo=v0*t-m*(R-r)*(2*sin(x(:,1))+x(:,1)-2*sin(th_0)-th_0)/(3*m+4*M);
hold on
plot(t,x(:,1),'r') %cilindro macizo
plot(t,xTubo,'b') %tubo
hold off
grid on
xlabel('t')
ylabel('\theta,x')
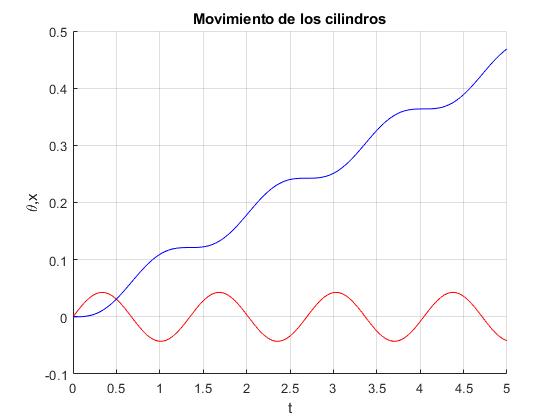
title('Movimiento de los cilindros')

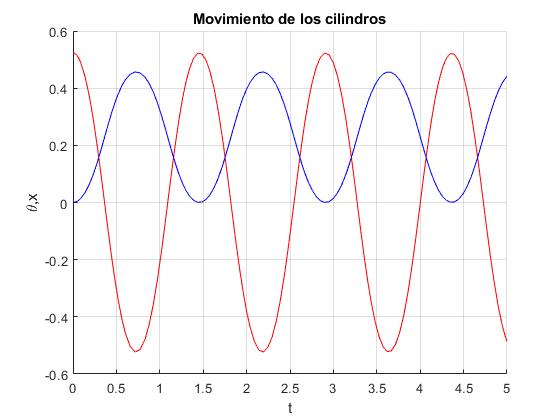
En azul, la posición angular θ del cilindro macizo, en rojo, la del tubo, x

Comprobamos que la energía inicial, es aproximadamente igual a la energía en cada instante

>> E0=3*m*(R-r)^2*wCilindro^2/4+m*9.8*(R-(R-r)*cos(th_0))
E0 =    6.8694
>> vTubo=v0-m*(R-r)*(2*cos(x(:,1))+1).*x(:,2)/(3*m+4*M);
>> E=3*m*(R-r)^2*x(:,2).^2/4+(3*m/4+M)*vTubo.^2+m*(R-r)*
(2*cos(x(:,1))+1).*x(:,2).*vTubo/2+m*9.8*(R-(R-r)*cos(x(:,1)))
E = 6.8694
    6.8694
    ......
    6.8555
    6.8555

Cambiamos en el script las condiciones iniciales

• El cilindro macizo se mantiene en la posición de equilibrio, θ₀=0 y se le proporciona una velocidad angular, (dθ/dt)₀=0.2

....
wCilindro=0.2; %velocidad angular inicial
th_0=0; %posición angular inicial
....

Observamos un comportamiento diferente, véase el programa interactivo al final de la página

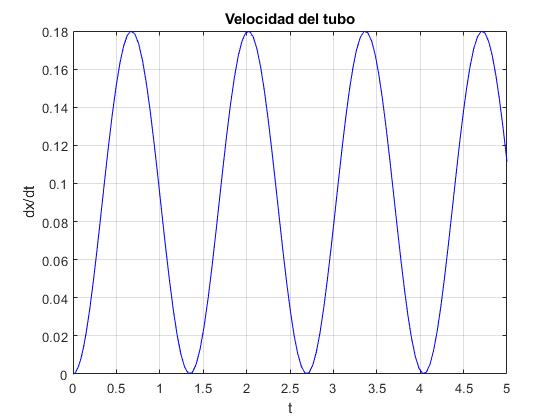
Representamos la velocidad dx/dt del tubo en función del tiempo, observamos los instantes en los que se detiene. La diferencia de dos tiempos consecutivos es un periodo, aproximadamente 1.34 s. Se puede comparar esta medida con el periodo calculado mediante las aproximación de pequeña amplitud (en el apartado que viene a continuación)

R=1; %radio superficie cilíndrica
r=0.25; %radio cilindro macizo
M=1; %masa superficie cilíndrica
m=2; %masa cilindro macizo

wCilindro=0.2;  %velocidad angular inicial
th_0=0; %posición angular inicial

v0=m*(R-r)*(2*cos(th_0)+1)*wCilindro/(3*m+4*M);
x0=[th_0,wCilindro];
f=@(t,x) [x(2); -2*(2*cos(x(1))+1)*sin(x(1))*m*x(2)^2/(3*(3*m+4*M)-
(2*cos(x(1))+1)^2*m)-2*9.8*sin(x(1))*(3*m+4*M)/((R-r)*(3*(3*m+4*M)-
(2*cos(x(1))+1)^2*m))]; 
[t,x]=ode45(f,[0,5],x0);
vTubo=v0-m*(R-r)*(2*cos(x(:,1))+1).*x(:,2)/(3*m+4*M);
plot(t,vTubo,'b') %tubo
grid on
xlabel('t')
ylabel('dx/dt')
title('Velocidad del tubo')

Aproximaciones

Cuando θ es pequeño sinθ≈θ, cosθ=1, θ(dθ/dt)²≈0

La ecuación diferencial en θ se transforma en

${\displaystyle \frac{1}{2}\left(R-r\right)\left(3-3^2\frac{m}{3m+4M}\right)\frac{d^2\theta }{d{t}^2}+g\theta =0}$

Que es la ecuación de un Movimiento Armónico Simple de frecuencia angular o periodo P=2π/ω

${\displaystyle {\omega }^2=\frac{g}{R-r}\frac{3m+4M}{6M}}$

>> w2=9.8*(3*m+4*M)/((R-r)*6*M)
w2 =   21.7778
>> 2*pi/sqrt(w2)
ans =    1.3464

Actividades

Se introduce

• La masa m del cilindro macizo, en el control titulado Masa cilindro macizo
• La posición angular inicial del centro del cilindro macizo θ₀, en el control titulado Posición
• La velocidad angular inicial del centro del cilindro macizo (dθ/dt)₀, en el control titulado Velocidad angular

Se ha fijado

• La masa M=1 y el radio R=1, del tubo que rueda sobre el plano horizontal
• El radio r=0.25 del cilindro macizo
• La posición inicial y velocidad inicial del tubo, ambos nulos

Se pulsa el botón titulado Nuevo

Se muestra el tubo de masa M y radio R rodando en el plano horizontal y el cilindro macizo de masa m y radio r rodando sin deslizar en su superficie interior

Se proporcionan los datos

• Tiempo t
• La posición x y velocidad dx/dt del centro del tubo
• La posición angular θ y la velocidad angular dθ/dt del cilindro macizo

Se sugiere probar estos dos ejemplos, observando las diferencias

• Posicición inicial θ₀=30°, velocidad angular inicial (dθ/dt)₀=0
• Posicición inicial θ₀=0, velocidad angular inicial (dθ/dt)₀=0.4

El lector puede medir el periodo de la oscilación utilizando los botones Pausa || y Paso a paso >|

El programa calcula en cada instante el tanto por ciento de error relativo en la energía o el cociente

${\displaystyle \left|\frac{E-E_0}{E_0}\right|·100}$

donde E es la energía del sistema en cualquier instante t, y E₀ es la energía inicial del sistema.

Este valor se proporciona en caracteres de color rojo en la parte izqiuerda. Su valor debe ser siempre cero, o un valor muy pequeño lo que indica que la energía del sistema permanece constante y el programa realiza los cálculos correctamente.

Referencias

Daniel Arovas. Lecture Notes on Classical Mechanics (A Work in Progress). University of California, San Diego. May 8, 2013, pp. 417-419. https://courses.physics.ucsd.edu/2010/Fall/physics200a/LECTURES/200_COURSE.pdf

Kirk T. McDonald. Cylinder Rolling inside Another Rolling Cylinder.
http://www.physics.princeton.edu/~mcdonald/examples/2cylinders_in.pdf .