La cicloide se produce cuando se hace rodar sin deslizar un disco sobre una superficie horizontal. Un punto del borde del disco describe una curva que se denomina cicloide (palabra griega que significa circular). A un giro del disco le corresponde un arco de la cicloide

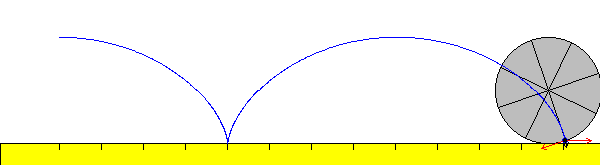
Si el punto P en el instante inicial está en la parte superior del disco, al cabo de un cierto tiempo t las coordenadas del punto P serán, tal como se muestra en la figura

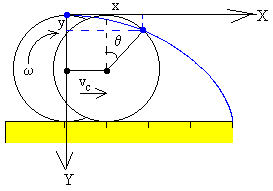
x=v_c·t+R·sinθ
y=R-R·cosθ

donde R es el radio del círculo y θ el ángulo girado en el tiempo t, θ=ω·t.

La relación entre la velocidad de traslación del centro de masas v_c y de rotación ω alrededor de un eje que pasa por el c.m. es v_c=ω·R.

La ecuaciones paramétricas de la cicloide son

x=R(θ +sinθ)
y=R(1-cosθ)

Oscilaciones de una partícula situada en el borde de un aro que rueda

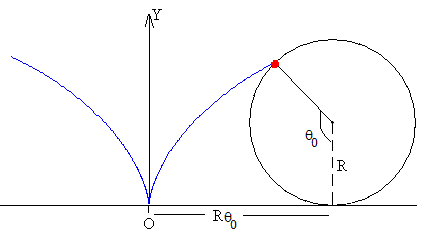
Supongamos que una partícula de masa m se sitúa en el bode de un aro de radio R, que supondremos de masa despreciable, y que rueda sin deslizar sobre una superficie horizontal. En la figura, se muestra la situación inicial:

• la partícula forma un ángulo θ₀ con la dirección vertical
• el centro del aro está a una distancia Rθ₀ del origen O, posición de equilibrio estable.

Trataremos de determinar la posición de la masa puntual a cabo de un cierto tiempo t, así como el periodo P de las oscilaciones que describe este sistema mecánico.

La condición de rodar sin deslizar, implica que el aro gira un ángulo θ, a la vez que su centro se traslada una distancia Rθ, tal como se muestra en la figura.

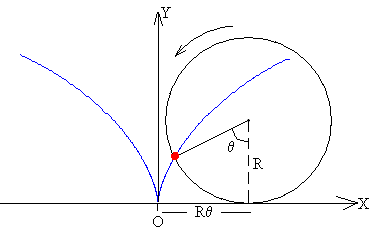
Las coordenadas de la partícula respecto al sistema de referencia, situado en la posición de equilibrio estable son

x=Rθ-Rsinθ
y=R-Rcosθ

Las componentes de la velocidad partícula se obtienen derivando, respecto del tiempo t, las coordenadas x e y.

${\displaystyle \begin{array}{l}{v}_x=\frac{dx}{dt}=R(1-\cos \theta )\frac{d\theta }{dt}\\ v_y=\frac{dy}{dt}=R\text{sin}\theta \frac{d\theta }{dt}\end{array}}$

Principio de conservación de la energía

La energía cinética es

${\displaystyle E_k=\frac{1}{2}m(v_x^2+v_y^2)=2m{R}^2{\left(\frac{d\theta }{dt}\right)}^2{\text{sin}}^{\text{2}}\frac{\theta }{2}}$

la energía potencial es

${\displaystyle E_p=mgy=2mgR{\text{sin}}^2\frac{\theta }{2}}$

La energía total, es la suma de ambas contribuciones, e igual a la energía potencial cuando la partícula se encuentra en el extremo de su trayectoria, θ=θ₀, dθ/dt=0.

${\displaystyle 2m{R}^2{\left(\frac{d\theta }{dt}\right)}^2{\text{sin}}^{\text{2}}\frac{\theta }{2}+2mgR{\text{sin}}^{\text{2}}\frac{\theta }{2}=2mgR{\text{sin}}^{\text{2}}\frac{{\theta }_0}{2}}$

Separando las variables t y θ, la ecuación del movimiento se escribe

${\displaystyle \frac{\text{-sin}(\theta /2)d\theta }{\sqrt{{\text{sin}}^2({\theta }_0/2)-{\text{sin}}^2(\theta /2)}}=\sqrt{\frac{g}{R}}dt}$

El signo menos aparece porque el ángulo θ disminuye con el tiempo. En el instante inicial t=0, la partícula se encuentra en la posición de máximo desplazamiento, θ=θ₀ y se dirige hacia el origen O.

Para integrar la ecuación diferencial, transformamos el denominador en otra forma equivalente mediante la relación sin²θ+cos²θ=1

${\displaystyle \frac{\text{-sin}(\theta /2)d\theta }{\sqrt{{\text{-cos}}^2({\theta }_0/2)+{\cos }^2(\theta /2)}}=\sqrt{\frac{g}{R}}dt}$

Haciendo el cambio de variable

${\displaystyle u=\frac{\cos (\theta /2)}{\cos ({\theta }_0/2)}{\displaystyle \underset{u_0}{\overset{u}{\int }}\frac{2du}{\sqrt{u^2-1}}}=\Omega t}$

donde u₀=1 es el valor de u para θ=θ₀, que es la posición inicial de partida tal como se muestra en la primera figura. Ω es la frecuencia angular de las oscilaciones de un péndulo de longitud igual al radio R de aro.

Esta integral es inmediata y puede consultarse en la tabla de integrales

${\displaystyle \ln \left|u+\sqrt{u^2-1}\right|-\ln u_0=\frac{\Omega t}{2}}$

Como 0≤θ/2≤θ₀/2≤π/2, se cumple que  u≥1

${\displaystyle u+\sqrt{u^2-1}=\exp \left(\frac{\Omega t}{2}\right)}$

Despejamos la raíz cuadrada, elevamos ambos miembros al cuadrado, simplificamos y despejamos u.

${\displaystyle u=\frac{\exp (\Omega t/2)+\exp (-\Omega t/2)}{2}=\cosh \left(\frac{\Omega t}{2}\right)}$

Finalmente, deshacemos el cambio de variable, para obtener la ecuación del movimiento.

cos(θ/2)=cos(θ₀/2)cosh(Ωt/2)

Periodo de las oscilaciones

El tiempo que tarda en alcanzar la posición θ=0, mide un cuarto del periodo P de este oscilador mecánico

1=cos(θ₀/2)cosh(ΩP/8),

De esta ecuación, despejamos el periodo P. Para ello, utilizamos la relación cosh²θ-sinh²θ=1

${\displaystyle \exp \left(\frac{\Omega P}{8}\right)=\frac{1+\text{sin}({\theta }_0/2)}{\cos ({\theta }_0/2)}P=8\sqrt{\frac{R}{g}}\ln \left(\frac{1+\text{sin}({\theta }_0/2)}{\cos ({\theta }_0/2)}\right)}$

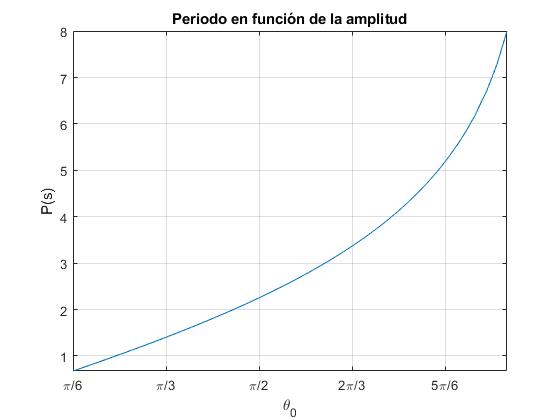
El periodo P es función del máximo desplzamiento angular, θ₀, tiende a cero cuando la amplitud se hace pequeña, a infinito cuando θ₀ tiende a 180º (posición de equilibrio inestable). En el péndulo simple, el periodo es función de la amplitud, pero es aproximadamente independiente de la amplitud cuando se separa ligeramente de la posición de equilibrio estable.

R=1; %radio que genera la cilcoide
P=@(x) (8*sqrt(R/9.8))*log((1+sin(x/2))./cos(x/2));
fplot(P, [30,170]*pi/180)
set(gca,'XTick',0:pi/6:pi)
set(gca,'XTickLabel',{'0','\pi/6','\pi/3','\pi/2','2\pi/3','5\pi/6','\pi'})
grid on
xlabel('\theta_0')
ylabel('P(s)')
title('Periodo en función de la amplitud')

Ecuaciones del movimiento

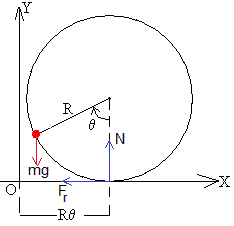
Como el aro no tiene masa, el centro de masa coincide con la posición de la partícula. La posición, velocidad y aceleración del centro de masas son

${\displaystyle \begin{array}{l}\{\begin{array}{l}{x}_c=R\theta -R\sin \theta \\ y_c=R-R\cos \theta \end{array}\\ \{\begin{array}{l}\frac{d{x}_c}{dt}=R\left(1-\cos \theta \right)\frac{d\theta }{dt}\\ \frac{d{x}_c}{dt}=R\sin \theta \frac{d\theta }{dt}\end{array}\\ \{\begin{array}{l}\frac{d^2{x}_c}{d{t}^2}=R\sin \theta {\left(\frac{d\theta }{dt}\right)}^2+R\left(1-\cos \theta \right)\frac{d^2\theta }{d{t}^2}\\ \frac{d^2{y}_c}{d{t}^2}=R\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+R\sin \theta \frac{d^2\theta }{d{t}^2}\end{array}\end{array}}$

Las fuerzas sobre el sistema formado por el aro y la partícula son:

• El peso, mg
• La reacción del plano horizontal, N
• La fuerza de rozamiento, F_r necesaria para que el aro ruede sin deslizar

Las ecuaciones del movimiento son

• Movimiento en la dirección horizontal
• Movimiento en la dirección vertical
• Rotación alrededor de un eje perpendicular al plano del aro y que pasa por el centro de masas

${\displaystyle \begin{array}{l}m\frac{d^2{x}_c}{d{t}^2}=-F_r\\ m\frac{d^2{y}_c}{d{t}^2}=N-mg\\ F_r{y}_c-N\left(R\theta -x_c\right)=I_c\frac{d^2\theta }{d{t}^2}\end{array}}$

El momento de inercia I_c=0, ya que la posición de la partícula coincide con el centro de masas

${\displaystyle \begin{array}{l}-\left(R\sin \theta {\left(\frac{d\theta }{dt}\right)}^2+R\left(1-\cos \theta \right)\frac{d^2\theta }{d{t}^2}\right)\left(R-R\cos \theta \right)-\left(g+R\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+R\sin \theta \frac{d^2\theta }{d{t}^2}\right)R\sin \theta =0\\ 2\sin \frac{\theta }{2}\frac{d^2\theta }{d{t}^2}+\left(\frac{g}{R}+{\left(\frac{d\theta }{dt}\right)}^2\right)\cos \frac{\theta }{2}=0\end{array}}$

Esta es la ecuación difeencial del movimiento

Ecuaciones de Lagrange

Hemos calculado la energía cinética y potencial del sistema formado por el aro y la partícula. La lagrangiana L es

${\displaystyle L=E_k-E_p=2m{R}^2{\left(\frac{d\theta }{dt}\right)}^2{\sin }^2\frac{\theta }{2}-2mgR{\sin }^2\frac{\theta }{2}}$

La ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \frac{d}{dt}\left(4m{R}^2\left(\frac{d\theta }{dt}\right){\sin }^2\frac{\theta }{2}\right)-2m{R}^2{\left(\frac{d\theta }{dt}\right)}^2\sin \frac{\theta }{2}\cos \frac{\theta }{2}+2mgR\sin \frac{\theta }{2}\cos \frac{\theta }{2}=0\\ 4m{R}^2\left(\frac{d^2\theta }{d{t}^2}\right){\sin }^2\frac{\theta }{2}+4m{R}^2{\left(\frac{d\theta }{dt}\right)}^2\sin \frac{\theta }{2}\cos \frac{\theta }{2}-2m{R}^2{\left(\frac{d\theta }{dt}\right)}^2\sin \frac{\theta }{2}\cos \frac{\theta }{2}+2mgR\sin \frac{\theta }{2}\cos \frac{\theta }{2}=0\\ 2\left(\frac{d^2\theta }{d{t}^2}\right)\sin \frac{\theta }{2}+{\left(\frac{d\theta }{dt}\right)}^2\cos \frac{\theta }{2}+\frac{g}{R}\cos \frac{\theta }{2}=0\end{array}}$

Obtenemos la misma ecuación diferencial del movimiento

Resolvemos la ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales: en el instante t=0, θ=θ₀, dθ/dt=0. Interrumpimos el procedimiento poco antes de llegar a θ=0, ya que en esa posición la aceleración angular se hace infinita y el procedimiento numérico deja de funcionar

function cicloide_mas
    R=1; %radio
    alfa=pi/2; %ángulo inicial
    f=@(t,x) [x(2); -(9.8/R+x(2)^2)*cos(x(1)/2)/(2*sin(x(1)/2))]; 
    opts=odeset('events',@stop_cicloide);
    [t,x]=ode45(f,[0,3],[alfa,0], opts);
    plot(t,x(:,1))
    grid on
    xlabel('t')
    ylabel('\theta');
    title('Oscilador')
    
   function [value,isterminal,direction]=stop_cicloide(t,x)
        value=x(1)-pi/360; %se detiene muy cerca del origen (a 0.5 grados)
        isterminal=1;    
        direction=-1; % 1 crece, -1 decrece, 0 no importa
   end
end

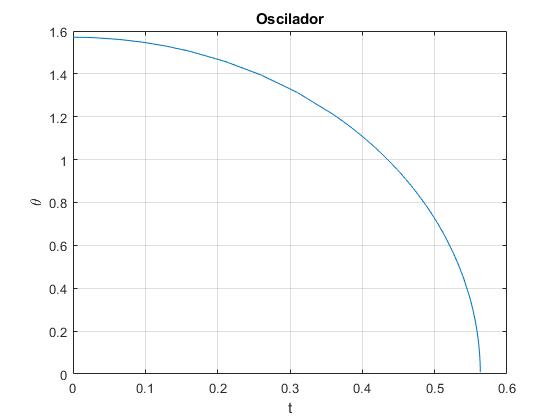
El tiempo de un cuarto de periodo es 0.5631 s, el periodo es 2.2524 s, el mismo valor que se obtendría por la fórmula del periodo

Actividades

Se introduce

• El ángulo inicial θ₀, en el control titulado Ángulo inicial
• El radio del aro se ha fijado en R=1 m

Se pulsa el botón titulado Nuevo

Se observa las oscilaciones de la partícula situada en el borde del aro que rueda sin deslizar.

Oscilaciones de un aro con un pequeño disco fijado en su interior

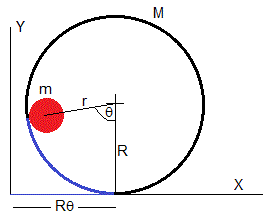
La situación descrita en el primer apartado no es realista, por lo que vamos a estudiar un sistema análogo formado por un aro de masa M, radio R y momento de inercia I_M y un disco sujeto al interior del aro cuyo centro dista r del centro del aro, su masa es m y su momento de inercia I_m

El aro rueda sin deslizar a lo largo del plano horizontal, cuando el aro se ha desplazado Rθ, ha girado un ángulo θ. La posición del centro del disco y del aro son, respectivamente

${\displaystyle \{\begin{array}{l}{x}_m=R\theta -r\sin \theta \\ y_m=R-r\cos \theta \end{array}\{\begin{array}{l}{x}_M=R\theta \\ y_M=R\end{array}}$

La posición, velocidad y aceleración del centro de masas es

${\displaystyle \begin{array}{l}\{\begin{array}{l}{x}_c=\frac{m{x}_m+M{x}_M}{m+M}=R\theta -\frac{m}{m+M}r\sin \theta \\ y_c=\frac{m{y}_m+M{y}_M}{m+M}=R-\frac{m}{m+M}r\cos \theta \end{array}\\ \{\begin{array}{l}\frac{d{x}_c}{dt}=\left(R-\frac{m}{m+M}r\cos \theta \right)\frac{d\theta }{dt}\\ \frac{d{x}_c}{dt}=\frac{m}{m+M}r\sin \theta \frac{d\theta }{dt}\end{array}\\ \{\begin{array}{l}\frac{d^2{x}_c}{d{t}^2}=\frac{m}{m+M}r\sin \theta {\left(\frac{d\theta }{dt}\right)}^2+\left(R-\frac{m}{m+M}r\cos \theta \right)\frac{d^2\theta }{d{t}^2}\\ \frac{d^2{y}_c}{d{t}^2}=\frac{m}{m+M}r\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+\frac{m}{m+M}r\sin \theta \frac{d^2\theta }{d{t}^2}\end{array}\end{array}}$

Ecuación del movimiento

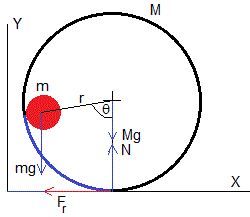
Las fuerzas sobre el sistema formado por el aro y el disco son:

• El peso, mg en el centro del disco y Mg en el centro del aro
• La reacción del plano horizontal, N en el punto de contacto
• La fuerza de rozamiento, F_r necesaria para que el aro ruede sin deslizar

Las ecuaciones del movimiento son

• Movimiento en la dirección horizontal
• Movimiento en la dirección vertical
• Rotación alrededor de un eje perpendicular al plano del aro y que pasa por el centro de masas

${\displaystyle \begin{array}{l}(m+M)\frac{d^2{x}_c}{d{t}^2}=-F_r\\ (m+M)\frac{d^2{y}_c}{d{t}^2}=N-(m+M)g\\ F_r{y}_c-N\left(R\theta -x_c\right)=I_c\frac{d^2\theta }{d{t}^2}\end{array}}$

El momento de inercia del sistema formado por el aro y el disco, respecto del centro de masas es

${\displaystyle \begin{array}{l}{I}_c=I_m+m\left({\left(x_m-x_c\right)}^2+{\left(y_m-y_c\right)}^2\right)+I_M+M\left({\left(x_M-x_c\right)}^2+{\left(y_M-y_c\right)}^2\right)=\\ I_m+I_M+m\left({\left(-\frac{M}{m+M}r\sin \theta \right)}^2+{\left(-\frac{M}{m+M}r\cos \theta \right)}^2\right)+M\left({\left(\frac{m}{m+M}r\sin \theta \right)}^2+{\left(\frac{m}{m+M}r\sin \theta \right)}^2\right)\\ I_c=I_m+I_M+\frac{mM}{m+M}{r}^2\end{array}}$

La fuerza de rozamiento F_r vale.

${\displaystyle F_r=-(m+M)\frac{d^2{x}_c}{d{t}^2}=-mr\sin \theta {\left(\frac{d\theta }{dt}\right)}^2-\left((m+M)R-mr\cos \theta \right)\frac{d^2\theta }{d{t}^2}}$

La reacción del plano N

${\displaystyle N=(m+M)g+mr\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+mr\sin \theta \frac{d^2\theta }{d{t}^2}}$

La ecuación del movimiento

${\displaystyle \begin{array}{l}\left\{-mr\sin \theta {\left(\frac{d\theta }{dt}\right)}^2-\left((m+M)R-mr\cos \theta \right)\frac{d^2\theta }{d{t}^2}\right\}\left(R-\frac{m}{m+M}r\cos \theta \right)-\\ \left\{(m+M)g+mr\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+mr\sin \theta \frac{d^2\theta }{d{t}^2}\right\}\left(\frac{m}{m+M}r\sin \theta \right)=\left(I_m+I_M+\frac{mM}{m+M}{r}^2\right)\frac{d^2\theta }{d{t}^2}\\ -mgr\sin \theta -mRr\sin \theta {\left(\frac{d\theta }{dt}\right)}^2-\left(\frac{m^2}{m+M}{r}^2+(m+M)R^2-2mrR\cos \theta \right)\frac{d^2\theta }{d{t}^2}=\left(I_m+I_M+\frac{mM}{m+M}{r}^2\right)\frac{d^2\theta }{d{t}^2}\\ \left(I_m+I_M+m{r}^2+(m+M)R^2-2mrR\cos \theta \right)\frac{d^2\theta }{d{t}^2}+mRr\sin \theta {\left(\frac{d\theta }{dt}\right)}^2+mgr\sin \theta =0\end{array}}$

La ecuación diferencial del movimiento es

${\displaystyle I(\theta )\frac{d^2\theta }{d{t}^2}+mRr\sin \theta {\left(\frac{d\theta }{dt}\right)}^2+mgr\sin \theta =0}$

Consideremos el sistema formado por el aro y la partícula, el aro tiene masa M=0 y momento de inercia I_M=0 y la partícula de masa m y momento de inercia I_m=0 situada en la interior del aro r=R

${\displaystyle \begin{array}{l}\left(2m{R}^2-2m{R}^2\cos \theta \right)\frac{d^2\theta }{d{t}^2}+m{R}^2\sin \theta {\left(\frac{d\theta }{dt}\right)}^2+mgR\sin \theta =0\\ 4{\sin }^2\frac{\theta }{2}\frac{d^2\theta }{d{t}^2}+2\sin \frac{\theta }{2}\cos \frac{\theta }{2}{\left(\frac{d\theta }{dt}\right)}^2+\frac{g}{R}2\sin \frac{\theta }{2}\cos \frac{\theta }{2}=0\\ 2\sin \frac{\theta }{2}\frac{d^2\theta }{d{t}^2}+\left(\frac{g}{R}+{\left(\frac{d\theta }{dt}\right)}^2\right)\cos \frac{\theta }{2}=0\end{array}}$

La misma ecuación del movimiento obtenida en el primer apartado

Energía

Energía cinética

${\displaystyle \begin{array}{l}{E}_k=\frac{1}{2}{I}_c{\left(\frac{d\theta }{dt}\right)}^2+\frac{1}{2}(m+M)\left({\left(\frac{d{x}_c}{dt}\right)}^2+{\left(\frac{d{y}_c}{dt}\right)}^2\right)=\\ \frac{1}{2}\left(I_m+I_M+\frac{mM}{m+M}{r}^2\right){\left(\frac{d\theta }{dt}\right)}^2+\frac{1}{2}(m+M)\left({\left(\left(R-\frac{m}{m+M}r\cos \theta \right)\right)}^2+{\left(\frac{m}{m+M}r\sin \theta \right)}^2\right){\left(\frac{d\theta }{dt}\right)}^2=\\ E_k=\frac{1}{2}\left(I_m+I_M+m{r}^2+(m+M)R^2-2mRr\cos \theta \right){\left(\frac{d\theta }{dt}\right)}^2\end{array}}$

Energía potencial. La energía potencial del aro no cambia

${\displaystyle E_p=mgr(1-\cos \theta )}$

Ecuaciones de Lagrange

La lagrangiana

${\displaystyle \begin{array}{l}L=E_k-E_p=\frac{1}{2}\left(I_m+I_M+m{r}^2+(m+M)R^2-2mRr\cos \theta \right){\left(\frac{d\theta }{dt}\right)}^2-mgr(1-\cos \theta )\\ =\frac{1}{2}I\left(\theta \right){\left(\frac{d\theta }{dt}\right)}^2-mgr(1-\cos \theta )\end{array}}$

La ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \frac{d}{dt}\left(I(\theta )\frac{d\theta }{dt}\right)-\frac{1}{2}\frac{dI(\theta )}{d\theta }{\left(\frac{d\theta }{dt}\right)}^2+mgr\sin \theta =0\\ I(\theta )\frac{d^2\theta }{d{t}^2}+2mRr\sin \theta {\left(\frac{d\theta }{dt}\right)}^2-mRr\sin \theta {\left(\frac{d\theta }{dt}\right)}^2+mgr\sin \theta =0\\ I(\theta )\frac{d^2\theta }{d{t}^2}+mRr\sin \theta {\left(\frac{d\theta }{dt}\right)}^2+mgr\sin \theta =0\end{array}}$

Obtenemos la misma ecuación diferencial del movimiento

Periodo

El máximo desplazamiento se produce cuando la velocidad angular dθ/dt=0, el ángulo girado es θ₀, la energía cinética es nula y la potencial E=mgr(1-cosθ₀) es igual a la total. Despejamos la velocidad angular

${\displaystyle \begin{array}{l}\frac{1}{2}\left(I_m+I_M+m{r}^2+(m+M)R^2-2mRr\cos \theta \right){\left(\frac{d\theta }{dt}\right)}^2+mgr(1-\cos \theta )=mgr(1-\cos {\theta }_0)\\ {\left(\frac{d\theta }{dt}\right)}^2=\frac{2mgr(\cos \theta -\cos {\theta }_0)}{I_m+I_M+m{r}^2+(m+M)R^2-2mRr\cos \theta }\\ {\left(\frac{d\theta }{dt}\right)}^2=\frac{2mgr(\cos \theta -\cos {\theta }_0)}{I+2mrR(1-\cos \theta )},I=I_m+I_M+M{R}^2+m{\left(R-r\right)}^2\\ {\left(\frac{d\theta }{dt}\right)}^2=\frac{mgr}{I}\frac{2(\cos \theta -\cos {\theta }_0)}{1+\frac{k}{2}(1-\cos \theta )},k=\frac{4mrR}{I}\end{array}}$

El periodo es cuatro veces el tiempo que tarda en desplazarse desde 0 a θ₀

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{P}{\int }}dt}=4\sqrt{\frac{I}{mgr}}{\displaystyle \underset{0}{\overset{{\theta }_0}{\int }}\sqrt{\frac{1+\frac{k}{2}(1-\cos \theta )}{2(\cos \theta -\cos {\theta }_0)}}}\\ P=4\sqrt{\frac{I}{mgr}}{\displaystyle \underset{0}{\overset{{\theta }_0}{\int }}\sqrt{\frac{1+k{\sin }^2\frac{\theta }{2}}{4\left({\sin }^2\frac{{\theta }_0}{2}-{\sin }^2\frac{\theta }{2}\right)}}}\end{array}}$

Hacemos el cambio de variable

${\displaystyle \begin{array}{l}\sin \frac{\theta }{2}=\sin (x)\sin \frac{{\theta }_0}{2}\\ \frac{1}{2}\cos \frac{\theta }{2}·d\theta =\cos (x)\sin \frac{{\theta }_0}{2}·dx\end{array}}$

La integral se transforma

${\displaystyle \begin{array}{l}P=4\sqrt{\frac{I}{mgr}}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\sqrt{\frac{1+k{\sin }^2(x){\sin }^2\frac{{\theta }_0}{2}}{4\left({\sin }^2\frac{{\theta }_0}{2}-{\sin }^{2}x·{\sin }^2\frac{{\theta }_0}{2}\right)}}}\frac{2\cos x·\sin \frac{{\theta }_0}{2}}{\sqrt{1-{\sin }^{2}x·{\sin }^2\frac{{\theta }_0}{2}}}dx\\ P=4\sqrt{\frac{I}{mgr}}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\sqrt{\frac{1+k{\sin }^2(x){\sin }^2\frac{{\theta }_0}{2}}{1-{\sin }^{2}x·{\sin }^2\frac{{\theta }_0}{2}}}}dx\\ P=P_0\frac{2}{\pi }{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\sqrt{\frac{1+k{\sin }^2(x){\sin }^2\frac{{\theta }_0}{2}}{1-{\sin }^{2}x·{\sin }^2\frac{{\theta }_0}{2}}}}dx,P_0=2\pi \sqrt{\frac{I}{mgr}}\end{array}}$

El máximo desplazamiento θ₀ ha de ser menor que π

Representamos el cociente P/P₀ en función del máximo desplazamiento θ₀, para varios valores del parámetro k. θ₀ tiene que ser algo menor que π para no producir error

th0=linspace(0,3,50);
P=zeros(1,length(th0));
hold on
for k=[0,0.5,1,2,8]
    i=1;
    for th_0=th0
        f=@(x) sqrt((1+k*sin(x).^2*sin(th_0/2)^2)./(1-sin(x).^2*sin(th_0/2)^2));
        P(i)=integral(f,0,pi/2)*2/pi;
        i=i+1;
    end
    plot(th0,P,'displayName',num2str(k))
end
set(gca,'XTick',0:pi/6:pi)
set(gca,'XTickLabel',{'0','\pi/6','\pi/3','\pi/2','2\pi/3','5\pi/6','\pi'})
xlabel('\theta_0')
ylabel('P/P_0')
legend('-DynamicLegend','location','best')
grid on
title('Periodo')

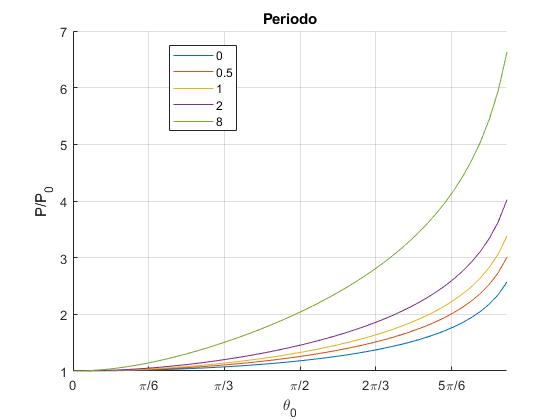
Cuando el momento de inercia I→0 o bien, k→∞, se obtiene el periodo para el sistema formado por el aro y la partícula estudiado en el primer apartado

Movimiento del sistema

Resolvemos la ecuación diferencial del movimiento para el siguiente sistema

• masa del aro, M=25 g
• radio del aro, R= 5 cm
• momento de inercia, I_M=MR²
• masa del disco, m=30 g
• distacia del centro del disco al centro del aro, r=R-0.8 cm
• radio del disco, 0.8 cm
• momento de inercia, I_m=m·0.8²/2 g·cm²

Representamos el desplazamiento angular θ en función del tiepo t durante un periodo P. Las condiciones iniciales son: en el instante t=0, el aro parte de la posición de máximo desplzamiento θ₀ con velocidad angular dθ/dt=0

M=25/1000; %masa aro
R=5/100; %radio aro
m=30/1000; %masa disco
r=R-8/1000; %posición disco
IM=M*R^2;
Im=m*(8/1000)^2/2;

%periodo
I=Im+IM+M*R^2+m*(R-r)^2;
k=4*m*r*R/I;
th_0=pi/2;
g=@(x) sqrt((1+k*sin(x).^2*sin(th_0/2)^2)./(1-sin(x).^2*sin(th_0/2)^2));
P=4*sqrt(I/(m*9.8*r))*integral(g,0,pi/2);

%movimiento
I0=Im+IM+m*r^2+(m+M)*R^2;
f=@(t,x) [x(2); -m*r*(9.8+R*x(2)^2)*sin(x(1))/(I0-2*m*r*R*cos(x(1)))]; 
[t,x]=ode45(f,[0,P],[th_0,0]);
plot(t,x(:,1))
grid on
xlabel('t')
ylabel('\theta');
title('Oscilador')

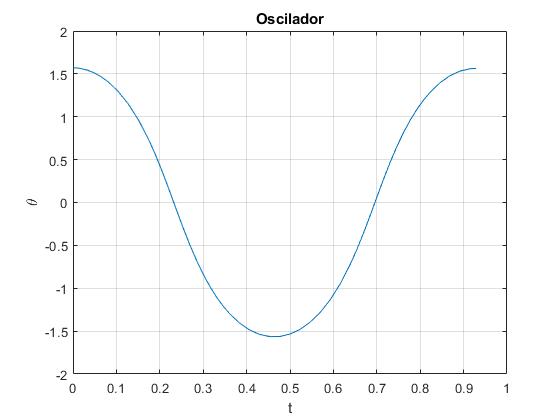
Verificamos que la energía se conserva

>> E0=m*9.8*r*(1-cos(th_0)) %inicial
E0 =    0.0123
>> E=(I0-2*m*r*R*cos(x(:,1))).*x(:,2).^2/2+m*9.8*r*(1-cos(x(:,1)))
E =
    0.0123
    0.0123
    ...
    0.0123
    0.0123    

Reacción N

Representamos la reacción del plano horizontal N/((M+m)g) en función del desplazamiento angular θ

${\displaystyle N=(m+M)g+mr\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+mr\sin \theta \frac{d^2\theta }{d{t}^2}}$

De la conservación de la energía, obtenemos el cuadrado de la velocidad angular (dθ/dt)². De la ecuación diferencial del movimiento, obtenemos la aceleración angular d²θ/dt²,

M=25/1000; %masa aro
R=5/100; %radio aro
m=30/1000; %masa disco
r=R-8/1000; %posición disco
IM=M*R^2;
Im=m*(8/1000)^2/2;
I0=Im+IM+m*r^2+(m+M)*R^2;

hold on
for th_0=[pi/4,pi/2, 3*pi/4]
    %cuadrado de la velocidad
    vel2=@(x) 2*m*9.8*r*(cos(x)-cos(th_0))./(I0-2*m*r*R*cos(x)); 
    %aceleración
    acel=@(x) -m*r*(9.8+R*vel2(x)).*sin(x)./(I0-2*m*r*R*cos(x));
    %reacción N
    N=@(x) ((m+M)*9.8+m*r*cos(x).*vel2(x)+m*r*sin(x).*acel(x))/((M+m)*9.8);
    fplot(N,[-th_0,th_0])
end   
hold off
set(gca,'XTick',-pi:pi/4:pi)
set(gca,'XTickLabel',{'-\pi','-3\pi/4','-\pi/2','-\pi/4','0','\pi/4',
'\pi/2','3\pi/4','\pi'})
legend('\pi/4', '\pi/2','3\pi/4','location','best')
grid on
xlabel('\theta_0')
ylabel('N/((M+m)g)');
title('Reacción N')

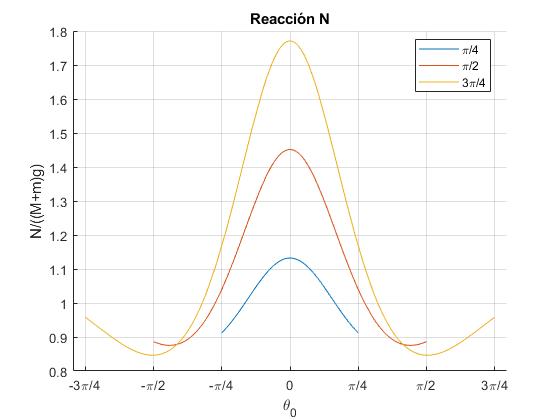
La característica más importante, es el máximo pronunciado de la reacción N cuando el disco pasa por el origen, θ=0, posición de equilibrio estable

Fuerza de rozamiento F_r

${\displaystyle F_r=-mr\sin \theta {\left(\frac{d\theta }{dt}\right)}^2-\left((m+M)R-mr\cos \theta \right)\frac{d^2\theta }{d{t}^2}}$

M=25/1000; %masa aro
R=5/100; %radio aro
m=30/1000; %masa disco
r=R-8/1000; %posición disco
IM=M*R^2;
Im=m*(8/1000)^2/2;
I0=Im+IM+m*r^2+(m+M)*R^2;

hold on
for th_0=[pi/4,pi/2, 3*pi/4]
    %cuadrado de la velocidad
    vel2=@(x) 2*m*9.8*r*(cos(x)-cos(th_0))./(I0-2*m*r*R*cos(x)); 
    %aceleración
    acel=@(x) -m*r*(9.8+R*vel2(x)).*sin(x)./(I0-2*m*r*R*cos(x));
    %Fuerza de rozamiento
    Fr=@(x) (m*r*sin(x).*vel2(x)+((M+m)*R-m*r*cos(x)).*acel(x))/((M+m)*9.8);
    fplot(Fr,[-th_0,th_0])
end   
hold off
set(gca,'XTick',-pi:pi/4:pi)
set(gca,'XTickLabel',{'-\pi','-3\pi/4','-\pi/2','-\pi/4','0','\pi/4',
'\pi/2','3\pi/4','\pi'})
legend('\pi/4', '\pi/2','3\pi/4','location','best')
grid on
xlabel('\theta_0')
ylabel('F_r/((M+m)g)');
title('Fuerza de rozamiento F_r')

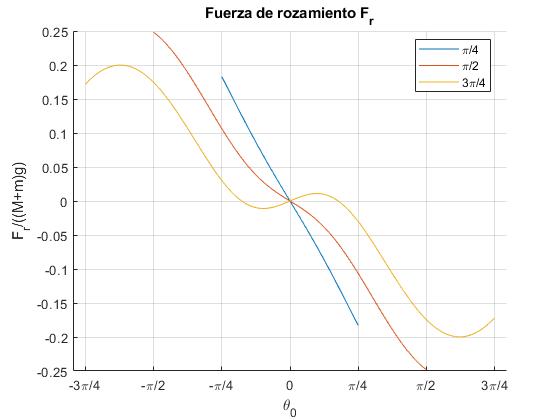
La fuerza de rozamiento suele ser negativa para θ>0, tal como se dibuja en la figura de las fuerzas, y positiva para θ<0. Se opone al movimiento de traslación del centro de masas. Para pequeños desplazamientos angulares iniciales θ₀, tiene un comportamiento lineal (línea de color azul). Para desplazamientos angulares iniciales grandes, el comportamiento es diferente

El análisis de la fuerza de rozamiento F_r y la reacción N es importante, para determinar el ángulo a partir del cual, el sistema formado aro y el disco empieza a deslizar, cuando la fuerza de rozamiento es igual o mayor que μ_sN

Referencias

Levy-Leblond J.M. Rock and roll: Non-isochronous small oscillations (an example). Am. J. Phys. 46 (1) January 1978, pp. 106-107

A. Filipponi. A non-isochronous rocking oscillator. Am. J. Phys. 82 (12), December 2014, pp. 1142-1148