Para amarrar un objeto, que eventualmente pueda ejercer una fuerza intensa, se ata el objeto al extremo de una soga y el otro extremo se enrolla a un poste firmemente fijado al suelo. Esto es lo que hacen los marineros cuando amarran un barco al muelle. La fuerza de rozamiento entre la soga y el poste es tanto mayor cuanto lo sea el ángulo (número de vueltas) de contacto entre ambos cuerpos

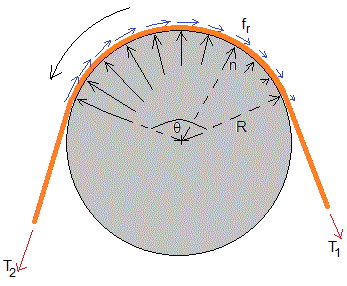
En la figura, se muestran las fuerzas normales n que se producen en cada uno de los puntos de contacto entre la cuerda y el cilindro y las correspondientes fuerzas de rozamiento f_r cuya dirección es tangente a la circunferencia de radio R y opuestas a la dirección de rotación. Esto reduce la tensión de la cuerda de modo que T₁<T₂

En esta página, vamos a establecer la relación entre las dos tensiones T₁ y T₂ y el ángulo de contacto θ de la cuerda con el cilindro cuando la cuerda está a punto de deslizar sobre el cilindro.

En la figura, se muestran las fuerzas sobre un elemento de cuerda de longitud R·Δθ, comprendido entre θ-Δθ/2 y θ+Δθ/2.

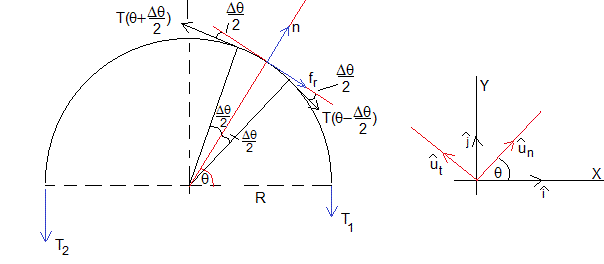
• La tensión que ejerce la parte izquierda de la cuerda T(θ+Δθ/2) sobre dicho elemento, su dirección es tangente a la circunferencia de radio R en la posición angular θ+Δθ/2, o bien hace un ángulo Δθ/2 con la dirección tangencial.

• La tensión que ejerce la parte derecha de la cuerda T(θ-Δθ/2) sobre dicho elemento, su dirección es tangente a la circunferencia de radio R en la posición angular θ-Δθ/2, o bien hace un ángulo Δθ/2 con la dirección tangencial.

• La reacción n de la superficie cilíndrica, cuya dirección es radial

• La fuerza de rozamiento f_r cuya dirección es tangencial y opuesta al movimiento de rotación

Formulamos las ecuaciones de equilibrio en la dirección tangencial

${\displaystyle T\left(\theta +\frac{\Delta \theta }{2}\right)\cos \frac{\Delta \theta }{2}-T\left(\theta +\frac{\Delta \theta }{2}\right)\cos \frac{\Delta \theta }{2}-f_r\Delta \theta =0}$

y en la dirección normal

${\displaystyle -T\left(\theta +\frac{\Delta \theta }{2}\right)\sin \frac{\Delta \theta }{2}-T\left(\theta -\frac{\Delta \theta }{2}\right)\sin \frac{\Delta \theta }{2}+n·\Delta \theta =0}$

Donde f_r y n tienen dimensiones de fuerza por unidad de ángulo en radianes

En el límite cuando Δθ→0, cos(Δθ/2)→1

${\displaystyle \begin{array}{l}{f}_r=\underset{\Delta \theta \to 0}{\lim }\frac{T\left(\theta +\frac{\Delta \theta }{2}\right)-T\left(\theta -\frac{\Delta \theta }{2}\right)}{\Delta \theta }=\frac{dT}{d\theta }\\ n=2T(\theta )\underset{\Delta \theta \to 0}{\lim }\frac{\sin \left(\frac{\Delta \theta }{2}\right)}{\Delta \theta }=T(\theta )\end{array}}$

Hemos calculado los módulos f_r y n, los vectores son

${\displaystyle \begin{array}{l}\overrightarrow{n}=T(\theta )·{\widehat{u}}_n=T(\theta )\left(\cos \theta ·\widehat{i}+\sin \theta ·\widehat{j}\right)\\ \overrightarrow{f_r}=-\frac{dT}{d\theta }{\widehat{u}}_t=-\frac{dT}{d\theta }\left(-\sin \theta ·\widehat{i}+\cos \theta ·\widehat{j}\right)=\frac{dT}{d\theta }\left(\sin \theta ·\widehat{i}-\cos \theta ·\widehat{j}\right)\end{array}}$

Fuerzas que ejerce el cilindro sobre la cuerda

Integramos entre 0 y π para calcular las fuerzas totales $\overrightarrow{F_r}$ y $\overrightarrow{N}$ que ejerce el cilindro sobre la cuerda

• Vector fuerza de rozamiento

${\displaystyle \overrightarrow{F_r}=\left({\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{dT}{d\theta }\sin \theta ·d\theta }\right)\widehat{i}-\left({\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{dT}{d\theta }\cos \theta ·d\theta }\right)\widehat{j}=}$

Integramos por partes la primera, la segunda es similar

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{dT}{d\theta }\sin \theta ·d\theta }\{\begin{array}{l}u=\sin \theta ,du=\cos \theta ·d\theta \\ dv=\frac{dT}{d\theta }d\theta ,v=T(\theta )\end{array}\\ {\displaystyle \int \frac{dT}{d\theta }\sin \theta ·d\theta }=T(\theta )·\sin \theta -{\displaystyle \int T(\theta )\cos \theta ·d\theta }\end{array}}$

El vector $\overrightarrow{F_r}$, es

${\displaystyle \begin{array}{l}\overrightarrow{F_r}=\left({T(\theta )\sin \theta |}_0^{\pi }-{\displaystyle \underset{0}{\overset{\pi }{\int }}T(\theta )·\cos \theta ·d\theta }\right)\widehat{i}-\left({T(\theta )\cos \theta |}_0^{\pi }+{\displaystyle \underset{0}{\overset{\pi }{\int }}T(\theta )·\sin \theta ·d\theta }\right)\widehat{j}=\\ =\left(-{\displaystyle \underset{0}{\overset{\pi }{\int }}T(\theta )·\cos \theta ·d\theta }\right)\widehat{i}-\left(-T(\pi )-T(0)+{\displaystyle \underset{0}{\overset{\pi }{\int }}T(\theta )·\sin \theta ·d\theta }\right)\widehat{j}=\\ \left(T_2+T_1\right)\widehat{j}-{\displaystyle \underset{0}{\overset{\pi }{\int }}T(\theta )\left(\cos \theta ·\widehat{i}+\sin \theta \widehat{j}\right)d\theta }\end{array}}$

Donde T₂=T(π) y T₁=T(0) son las fuerzas que se ejercen sobre la porción de cuerda de longitud πR enrollada en el cilindro en dichas posiciones, θ=0 y π

• Vector fuerza normal

${\displaystyle \overrightarrow{N}={\displaystyle \underset{0}{\overset{\pi }{\int }}T(\theta )\left(\cos \theta ·\widehat{i}+\sin \theta ·\widehat{j}\right)d\theta }}$

La suma de las dos fuerzas que ejerce el cilindro sobre la cuerda es

${\displaystyle {\overrightarrow{F}}_r+\overrightarrow{N}=\left(T_2+T_1\right)\widehat{j}}$

Momentos respecto del eje del cilindro

• La fuerza normal $\overrightarrow{n}$ no produce momento, ya que su dirección es radial
• El momento de la fuerza $\overrightarrow{f_r}$ cuya dirección es tangencial es f_r·R

El momento total respecto del eje del cilindro es

${\displaystyle {\displaystyle \underset{0}{\overset{\pi }{\int }}R·\frac{dT}{d\theta }}d\theta =R\left(T(\pi )-T(0)\right)=R(T_2-T_1)}$

La cuerda a punto de deslizar sobre el cilindro

Cuando la cuerda está a punto de deslizar se cumple que f_r=μ·n

donde μ es el coeficiente estático

Esta relación implica que todos los puntos θ de la cuerda alcanzan esta condición simultáneamente, ya que la cuerda es inextensible.

${\displaystyle \begin{array}{l}\frac{dT}{d\theta }=\mu T(\theta )\\ T(\theta )=T(0)e^{\mu \theta }=T_1{e}^{\mu \theta }\end{array}}$

Como T(π)=T₂, tenemos

${\displaystyle T_2=T_1{e}^{\mu \pi }}$

Ahora, ya podemos calcular el vector $\overrightarrow{F_r}$ que ejerce el cilindro sobre la cuerda cuando está a punto de deslizar (máximo valor de la fuerza de rozamiento)

${\displaystyle \begin{array}{l}\overrightarrow{F_r}=\left(T_2+T_1\right)\widehat{j}-{\displaystyle \underset{0}{\overset{\pi }{\int }}{T}_1{e}^{\mu \theta }\left(\cos \theta ·\widehat{i}+\sin \theta \widehat{j}\right)d\theta }=\\ \left(T_2+T_1\right)\widehat{j}-{T_1\frac{\mu e^{\mu \theta }}{\left({\mu }^2+1\right)}\left\{\left(\cos \theta +\frac{1}{\mu }\sin \theta \right)\widehat{i}+\left(\sin \theta -\frac{1}{\mu }\cos \theta \right)\widehat{j}\right\}|}_0^{\pi }=\\ \left(T_2+T_1\right)\widehat{j}-T_1\frac{\mu }{\left({\mu }^2+1\right)}\left(1+e^{\mu \pi }\right)\left\{-\widehat{i}+\frac{1}{\mu }\widehat{j}\right\}=\left(T_2+T_1\right)\widehat{j}-T_1\frac{\mu }{\left({\mu }^2+1\right)}\left(1+\frac{T_2}{T_1}\right)\left\{-\widehat{i}+\frac{1}{\mu }\widehat{j}\right\}=\\ \frac{\mu }{\left({\mu }^2+1\right)}\left(T_2+T_1\right)\left(\widehat{i}+\mu \widehat{j}\right)\end{array}}$

Ejemplos

En general, la relación entre T₂ y T₁ es

${\displaystyle T_2=T_1{e}^{\mu \theta }}$

donde θ es el ángulo de contacto entre la cuerda y el cilindro

Problema 1

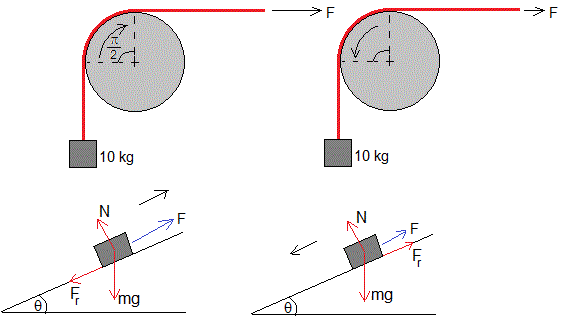
Para que el cuerpo de masa m esté en equlibrio en reposo sobre el plano inclinado, (véase el apartado Ejercicios de la página dedicada al estudio de la Fuerza de rozamiento) la fuerza F que aplicamos no deberá superar un valor máximo ni ser inferior a un valor mínimo, es decir, deberá estar comprendida en el intervalo (F_máx, F_mín)

F_máx=mgsinθ+μ_smgcosθ (figura inferior izquierda)
F_mín=mgsinθ-μ_smgcosθ (figura inferior derecha)

Siendo μ_s=0.3 es el coeficiente estático

• Del mismo modo, en el movimiento de rotación, el valor máximo se obtiene en la figura de la izquierda, identificando T₂=F, T₁=10·9.8, θ=π/2

${\displaystyle \frac{F_{máx}}{10·9.8}=\exp \left(0.3\frac{\pi }{2}\right),F_{máx}=157\text{N}}$

• El valor mínimo, se obtiene en la figura de la derecha, identificando T₂=10·9.8, T₁=F

${\displaystyle \frac{10·9.8}{F_{\min }}=\exp \left(0.3\frac{\pi }{2}\right),F_{\min }=61.2\text{N}}$



• Supongamos que F=50 N, determinar el valor mínimo del ángulo α para que el peso de 10 kg no caiga.

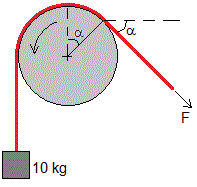
Identificando T₂=10·9.8, T₁=F, θ=π/2+α

${\displaystyle \frac{10·9.8}{50}=\exp \left(0.3\left(\alpha +\frac{\pi }{2}\right)\right),{\alpha }_{\min }=38.5º}$

Problema 2

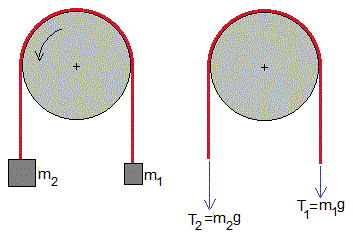
Calcular el coeficiente estático μ_s mínimo que impide el deslizamiento de la cuerda enrollada en el cilindro. Datos, m₂=10 kg, m₁=5 kg

${\displaystyle \begin{array}{l}{T}_2=T_1{e}^{{\mu }_s\pi }\\ {\mu }_s=\frac{1}{\pi }\ln \left(\frac{T_2}{T_1}\right)=\frac{1}{\pi }\ln \left(\frac{m_2}{m_1}\right)\end{array}}$

El resultado es μ_s=0.2206 para el coeficiente estático

Supongamos que incrementamos la masa m₂>m₁exp(πμ_s), la cuerda desliza sobre el cilindro, las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}\{\begin{array}{l}{m}_{2}g-T_2=m_{2}a\\ T_1-m_{1}g=m_{1}a\\ T_2=T_1\exp \left({\mu }_k\pi \right)\end{array}\\ a=\frac{m_2-m_1{e}^{{\mu }_k\pi }}{m_2+m_1{e}^{{\mu }_k\pi }}g\end{array}}$

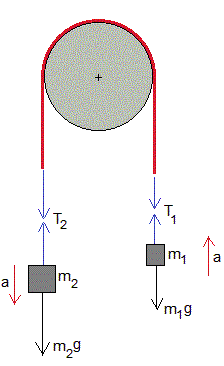
Donde μ_k es el coeficiente cinético. Supondremos que la relación entre las tensiones derivada para el caso estático se mantiene cuando ambos cuerpos (cuerda y cilindro) están en movimiento relativo

Supongamos que m₂=15 kg. La aceleración de las pesas es a=1.96 m/s²

La aceleración a es positiva ya que m₂>m₁exp(μ_sπ) en caso contrario la cuerda permanece en reposo, la tensión T₂=m₂g no supera el valor máximo m₁g·exp(μ_sπ)

Comparamos con el caso más simple, una máquina de Atwood con una polea ideal de masa despreciable

${\displaystyle \begin{array}{l}\{\begin{array}{l}{m}_{2}g-T_1=m_{2}a\\ T_1-m_{1}g=m_{1}a\end{array}\\ a=\frac{m_2-m_1}{m_2+m_1}g\end{array}}$

Con los datos m₂=15 kg, m₁=5 kg la aceleración es a=4.9 m/s²

La máquina de Atwood

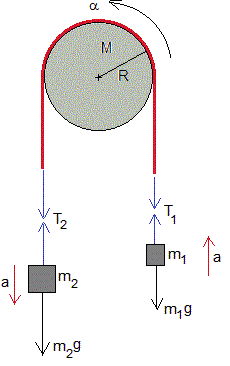
La máquina de Atwood, consta de una polea de masa M y radio R. Si tiene forma de disco su momento de inercia es I=MR²/2

Las pesas que cuelgan del hilo inextensible y de masa despreciable tienen masas m₂ y m₁, respectivamente

Las ecuaciones del movimiento de las pesas y de la polea son

${\displaystyle \{\begin{array}{l}{m}_{2}g-T_2=m_{2}a\\ T_1-m_{1}g=m_{1}a\\ T_{2}R-T_{1}R=\left(\frac{1}{2}M{R}^2\right)\alpha \end{array}}$

Analizamos tres situaciones:

• La cuerda no desliza sobre la polea, se cumple que a=α·R

Resolvemos el sistema de ecuaciones

${\displaystyle \begin{array}{l}a=\frac{m_2-m_1}{m_2+m_1+\frac{1}{2}M}g,\\ T_2=\frac{2m_1+\frac{1}{2}M}{m_2+m_1+\frac{1}{2}M}{m}_{2}g,T_1=\frac{2m_2+\frac{1}{2}M}{m_2+m_1+\frac{1}{2}M}{m}_{1}g\end{array}}$

• En la situación límite, la fuerza de rozamiento alcanza su valor máximo y la cuerda está a punto de deslizar sobre la polea. Se cumple

${\displaystyle \begin{array}{l}a=\alpha R\\ \frac{T_2}{T_1}=e^{{\mu }_s\pi }\end{array}}$

Calculamos la masa crítica de la polea

${\displaystyle \begin{array}{l}\frac{\left(4m_1+M\right)m_2}{\left(4m_2+M\right)m_1}=\exp \left({\mu }_s\pi \right)\\ M_c=\frac{4m_2{m}_1\left(e^{{\mu }_s\pi }-1\right)}{m_2-m_1{e}^{{\mu }_s\pi }}\end{array}}$

Por ejemplo, si m₁=1 kg, m₂= 3 kg y μ_s=0.3, se obtiene que M_c=43.3 kg

Supongamos ahora, que cambiamos la masa de la polea M=40 kg (menor que M_c)

mu=0.3;  %coeficiente estático
m1=1; %pesas
m2=3;
M=40; %masa polea
a=(m2-m1)*9.8/(m2+m1+M/2); %aceleración
T2=(2*m1+M/2)*m2*9.8/(m2+m1+M/2); %tensiones
T1=(2*m2+M/2)*m1*9.8/(m2+m1+M/2);
T2m=T1*exp(mu*pi); %valor máximo de la tensión
disp([T2, T2m])

   26.9500    27.2459

La tensión T₂=26.95 N. El valor máximo de la tensión justo en el momento en que la cuerda empieza a deslizar sobre la polea es T₁exp(πμ_s)=27.25 N. La tensión T₂ es inferior a la máxima, la cuerda no desliza sobre la polea.

• Si la masa de la polea M>M_c, la cuerda puede deslizar sobre la polea

Para que la cuerda deslice sobre la polea se tiene que cumplir que m₂>m₁exp(μ_sπ) al igual que la polea en reposo (problema 2) y esta condición es independiente de la masa M de la polea

Si la cuerda desliza, ya no se cumple la relación entre aceleraciones, a≠α·R. La relación entre las tensiones es

${\displaystyle \frac{T_2}{T_1}=e^{{\mu }_k\pi }}$

Junto con las ecuaciones del movimiento, nos permite calcular la aceleración a de las pesas y la aceleración angular del disco α

${\displaystyle \begin{array}{l}a=\frac{m_2-m_1{e}^{{\mu }_k\pi }}{m_2+m_1{e}^{{\mu }_k\pi }}g,T_1=\frac{2m_2{m}_1}{m_2+m_1{e}^{{\mu }_k\pi }}g\\ \alpha R=\frac{2m_2{m}_1\left(e^{{\mu }_k\pi }-1\right)}{M\left(m_2+m_1{e}^{{\mu }_k\pi }\right)}g\end{array}}$

La aceleración a tiene el mismo valor que el que se obtuvo considerando la polea en reposo (problema 2). Es independiente de la masa M de la polea

Cuando la masa M de la polea es muy grande, su aceleración angular tiende a cero.

Supongamos que m₁=1 kg, m₂= 3 kg, M=50 kg y μ_k=0.3.

mu=0.3;  %coeficiente cinético
m1=1; %pesas
m2=3;
M=50; %masa polea, mayor que la crítica
a=(m2-m1*exp(mu*pi))*9.8/(m2+m1*exp(mu*pi));
T1=2*m1*m2*9.8/(m2+m1*exp(mu*pi));
T2=T1*exp(mu*pi);
alfaR=2*m1*m2*9.8*(exp(mu*pi)-1)/(M*(m2+m1*exp(mu*pi)));
%límite para deslizar
disp([a, alfaR])

  0.7635    0.3309

La cuerda desliza sobre la polea, la aceleración de las pesas es a=0.76 m/s² y la tangencial de un punto del borde de la polea α·R=0.33 m/s²

Si incrementamos el coeficiente estático a μ_s=0.5, deja de cumplirse la relación m₂>m₁exp(μ_sπ), (3<4.81) la tensión de la cuerda T₂=m₂g no supera el valor máximo m₁g·exp(μ_sπ), la cuerda permenece en reposo sobre la polea, estamos en el primer caso.

Actividades

Se introduce

• La masa M de la polea, en el control titulado Masa polea M
• El coeficiente estático μ_s y cinético μ_k con el mismo valor, en el control titulado Coef. rozamiento μ
• La masa de la pesa derecha se ha fijado en m₁=1 kg y la izquierda en m₂=3 kg

Para m₁=1 kg, m₂=3 kg y μ=0.3, la masa crítica de la polea es M_c=43.3 kg

• Si la masa de la polea M es menor que M_c la cuerda no desliza
• Si la masa de la polea M es mayor que M_c la cuerda desliza

En la parte derecha, se proporcionan los datos de

• El tiempo t
• La altura de la pesa izquierda de masa m₂
• La aceleración a de las pesas
• La aceleración tangencial αR de un punto del borde de la polea
• La tensión T₁ de la parte derecha de la cuerda
• La tensión T₂ de la parte izquierda de la cuerda
• El valor máximo de T₂=T₁exp(μ_sπ)

Los puntos de color azul claro sobre la cuerda nos permiten apreciar el movimiento relativo de la cuerda respecto de la polea por ejemplo, para M=45 y μ=0.3

Referencias

Thiago R. de Oliveira, Nivaldo A. Lemos. Force and torque of a string on a pulley. Am. J. Phys. 86 (4), April 2018. pp. 275-279

J. L. Meriam, L. G. Kraige. Engineering Mechanics, Volume 1, Statics. Seventh Edition, John Wiley & Sons, Inc. 2006, pp. 379