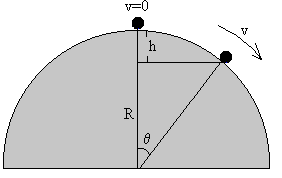
Una cúpula semiesférica fija

La partícula se encuentra inicialmente en reposo sobre el vértice de la cúpula, en una posición de equilibrio inestable. Cuando se desvía ligeramente de esta posición, la partícula desliza sin rozamiento, incrementando su velocidad hasta que llega un momento en el que deja de estar en contacto con la cúpula. En este apartado, calcularemos la posición θ_c para la cual la reacción N de superficie semiesférica es nula.

Conservación de la energía

La energía de la partícula en la posición inicial θ=0, es

E_i=mgR

La energía de la partícula en la posición θ es

${\displaystyle E_f=\frac{1}{2}m{v}^2+mgR\cos \theta }$

Aplicando el principio de conservación de la energía E_i=E_f, calculamos la velocidad del móvil v en la posición θ

${\displaystyle v^2=2gR(1-\cos \theta )v=2\sqrt{gR}\sin \left(\frac{\theta }{2}\right)}$

Dinámica

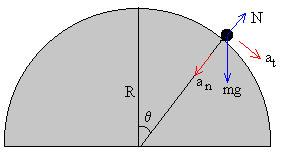
Las fuerzas que actúan sobre la partícula son

• el peso mg
• la reacción de la cúpula N.

La partícula describe un movimiento circular con aceleración tangencial a_t y aceleración normal a_n. Estas aceleraciones se determinan aplicando la segunda ley de Newton a un movimiento circular de radio R

• Ecuación del movimiento en la dirección tangencial

mg·sinθ=ma_t

• Ecuación del movimiento en la dirección normal

mg·cosθ-N=ma_n

La segunda ecuación, junto al principio de conservación de la energía, nos permite calcular la reacción del plano N, en la posición θ

${\displaystyle N=mg\cos \theta -m\frac{v^2}{R}N=3mg\cos \theta -2mg}$

La partícula deja de estar en contacto con la cúpula cuando la reacción N se anule. Para el ángulo θ_c tal que

${\displaystyle \cos {\theta }_c=\frac{2}{3}}$

Aproximadamente, 48º medidos desde la vertical. Como vemos el ángulo límite es independiente del radio de la cúpula, de la masa de la partícula y de la aceleración de la gravedad g.

La velocidad de la partícula cuando alcanza en esta posición es

${\displaystyle v_c^2=\frac{2}{3}gR}$

Ecuación del movimiento

La ecuación del movimiento en la dirección tangencial, nos permite calcular la posición angular θ en función del tiempo t.

${\displaystyle R\frac{d^2\theta }{d{t}^2}=g\sin \theta }$

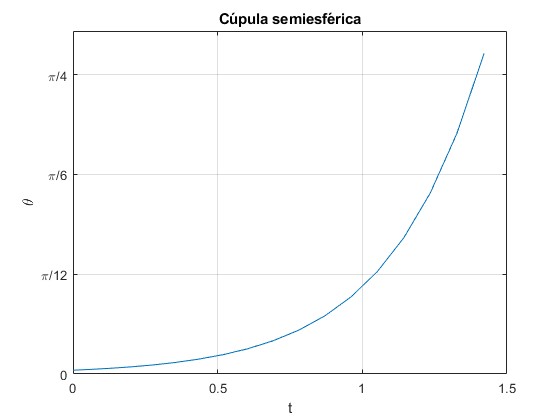
Que se resuelve por procedimientos numéricos. Si se establece las condiciones iniciales t=0, θ=0, dθ/dt=0. La partícula permanece todo el tiempo en esta posición de equilibrio inestable. Las condiciones iniciales serán t=0, θ=θ₀, dθ/dt=ω₀.Donde θ₀ es un pequeño ángulo y ω₀ es la velocidad angular de la partícula correspondiente a este ángulo, que se calcula aplicando el principio de conservación de la energía. En la figura, se representa la posición θ de la partícula en grados, en función del tiempo t

function cupula_5  
    R=1; %radio
    th_c=acos(2/3); %ángulo crítico
    x0=[0.01,sqrt(9.8/R)*2*sin(0.01/2)]; %posición, velocidad inicial
    f=@(t,x) [x(2);9.8*sin(x(1))/R]; 
    opts=odeset('events',@(t,x) stop_cupula(t,x));
    [t,x]=ode45(f,[0,50],x0,opts);
    plot(t,x(:,1)*180/pi)
    grid on
    set(gca,'YTick',0:pi/12:pi/2)
    set(gca,'YTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
    xlabel('t')
    ylabel('\theta')
    title('Cúpula semiesférica')

    function [value,isterminal,direction]=stop_cupula(~,x)
        value=x(1)-th_c; 
        isterminal=1;
        direction=1; 
    end
end

El procedimiento de cálculo se termina cuando se alcanza la posición final θ_c=arccos(2/3), para ello se define la función

Movimiento bajo la aceleración constante de la gravedad

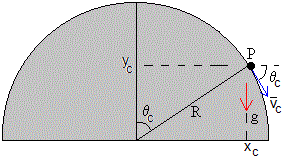
Una vez que la partícula deja de tener contacto con la cúpula, se mueve bajo la acción de su propio peso, es decir, describe una trayectoria parabólica desde el punto de coordenadas

x_c=R·sinθ_c
y_c=R·cosθ_c

Con velocidad inicial

${\displaystyle \begin{array}{l}{v}_{0x}=v_c\cos \theta \\ v_{0y}=v_c\sin \theta \end{array}}$

Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}x=x_c+v_c\cos \theta t\\ y=y_c-v_c\sin \theta t-\frac{1}{2}g{t}^2\end{array}}$

El punto de impacto sobre el suelo se calcula poniendo y=0 en la segunda ecuación, despejando el tiempo t y sustituyéndolo en la primera.

Ejemplo:

Sea el radio de la cúpula es R=1 m. En el momento en el que la partícula deja de tener contacto con la cúpula N=0, su posición angular es cosθ= 2/3 y su velocidad es,

${\displaystyle v_c=\sqrt{\frac{2}{3}9.8·1}=2.56\text{m/s}}$

Cuando llega al suelo y=0. Se resuelve la ecuación de segundo grado t=0.222 s

Se calcula el alcance medido desde el centro de la cúpula x=1.12 m

R=1;
angulo=acos(2/3);
v0=sqrt(2*R*9.8/3);
%tiempo que tarda en llegar al suelo, y=0
t=(sqrt((v0*sin(angulo))^2+2*9.8*R*cos(angulo))-v0*sin(angulo))/9.8;
%alcance
x=R*sin(angulo)+v0*cos(angulo)*t

x =1.1246

Actividades

El radio R de la cúpula se ha fijado en 1 m

Se pulsa el botón Nuevo.

El círculo situado en la parte superior izquierda representa la energía total de la partícula, la porción de color rojo representa la energía cinética, y la porción azul, la energía potencial. Observamos que la energía potencial se va transformando en energía cinética, pero la suma de los valores de ambas clases de energía se mantiene constante a lo largo de la trayectoria de la partícula.

Mediante una línea roja a trazos se señala el ángulo límite arccos(2/3), para el cual la reacción N=0

Solución analítica

La energía de la partícula en la posición inicial θ=0, es

${\displaystyle E=\frac{1}{2}m{v}_0^2+mgR}$

donde v₀ es la velocidad inicial de la partícula. La energía de la partícula en la posición θ, es

${\displaystyle E=\frac{1}{2}m{v}^2+mgR\cos \theta }$

La reacción N de la cúpula es

${\displaystyle N=mg\cos \theta -m\frac{v^2}{R}=3mg\cos \theta -2mg-m\frac{v_0^2}{R}}$

Se anula para el ángulo crítico θ_c

${\displaystyle \cos {\theta }_c=\frac{2}{3}+\frac{1}{3}\frac{v_0^2}{gR}}$

A partir del principio de conservación de la energía, obtenemos la relación implícita entre la posición angular θ y el tiempo t

${\displaystyle \begin{array}{l}E=\frac{1}{2}m{\left(R\frac{d\theta }{dt}\right)}^2+mgR\cos \theta \\ \frac{d\theta }{dt}=\sqrt{\frac{2g}{R}}\sqrt{\frac{E}{mgR}-\cos \theta }\\ {\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{d\theta }{\sqrt{\frac{E}{mgR}-\cos \theta }}}=\sqrt{\frac{2g}{R}}{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ t=\sqrt{\frac{R}{2g}}{\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{d\theta }{\sqrt{\frac{E}{mgR}-\cos \theta }},\theta \le {\theta }_c}\end{array}}$

Buscamos, en el libro titulado 'Table of Integrals, Series, and Products' la solución a integrales de este tipo y la encontramos en el apartado 2.571, n° 5 de la página 179

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{dx}{\sqrt{a-b\cos x}}=\frac{2}{\sqrt{a+b}}}F\left(\delta ,r\right),a>b>\mathrm{0,}0\le x\le \pi \\ \{\begin{array}{l}r=\sqrt{\frac{2b}{a+b}}\\ \delta =\arcsin \sqrt{\frac{\left(a+b\right)\left(1-\cos x\right)}{2\left(a-b\cos x\right)}}\end{array}\end{array}}$

Para este problema,

${\displaystyle \begin{array}{l}a=\frac{E}{mgR}=1+\frac{v_0^2}{2gR}>1\\ b=1\end{array}}$

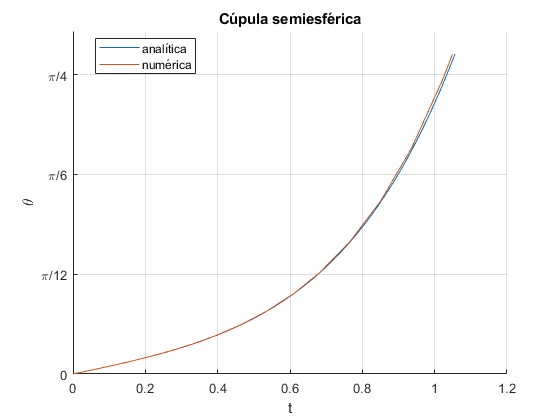
Comparamos la solución analítica y numérica para una cúpula de radio R=1 m. La velocidad de la partícula en el vértice de la cúpula θ=0, es v₀=0.5 m/s

function cupula_4   
    R=1; %radio
    v0=0.2; %velocidad inicial
    th_c=acos(2/3+v0^2/(3*9.8*R)); %ángulo crítico
    a=1+v0^2/(2*9.8*R);
    b=1;
    r=sqrt(2*b/(a+b));
    xx=linspace(0,th_c,100);
    t=zeros(1,length(xx));
    i=1;
    for x=xx
        delta=asin(sqrt((a+b)*(1-cos(x))/(2*(a-b*cos(x)))));
        t(i)=sqrt(R/19.6)*2*ellipticF(delta,r)/sqrt(a+b);
        i=i+1;
    end
    hold on
    plot(t,xx)
    f=@(t,x) [x(2);9.8*sin(x(1))/R]; 
    opts=odeset('events',@(t,x) stop_cupula(t,x));
    [t,x]=ode45(f,[0,50],[0,v0/R],opts);
    plot(t,x(:,1))

    hold off
    grid on
    set(gca,'YTick',0:pi/12:pi/2)
    set(gca,'YTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
    legend('analítica','numérica','location','best')
    xlabel('t')
    ylabel('\theta')
    title('Cúpula semiesférica')

    function [value,isterminal,direction]=stop_cupula(~,x)
        value=x(1)-th_c; 
        isterminal=1;
        direction=1; 
    end
end

Movimiento en una pista de forma f(x)

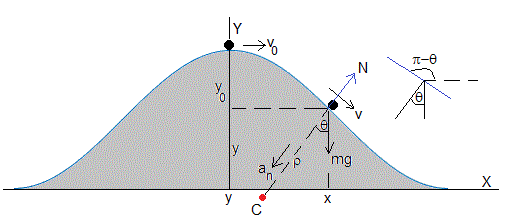
Consideremos una pista con la forma dada por la función f(x) en un intervalo dado. Lanzamos la partícula en el punto más alto con velocidad inicial v₀, queremos conocer si la partícula se saldrá de la pista. Si hay algún punto x donde la reacción se anule, N=0

Aplicando el principio de conservación de la energía, calculamos la velocidad v de la partícula en una punto de abscisa x es

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}_0^2+mg{y}_0=mgy+\frac{1}{2}m{v}^2\\ v^2=v_0^2+2g\left(y_0-y\right)\end{array}}$

Dibujamos la dirección normal, la aceleración normal apunta al centro de curvatura C, sea ρ el radio de curvatura.

${\displaystyle \rho =\frac{{\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}^{3/2}}{\left|\frac{d^{2}y}{d{x}^2}\right|}}$

La ecuación del movimiento en la dirección normal es

${\displaystyle mg\cos \theta -N=m\frac{v^2}{\rho }}$

π-θ es el ángulo que forma la tangente a la pista en el punto (x,y) con la horizontal, tan(π-θ)=dy/dx

${\displaystyle \cos \theta =\frac{1}{\sqrt{1+{\tan }^2\theta }}=\frac{1}{\sqrt{1+{\tan }^2\left(\pi -\theta \right)}}=\frac{1}{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}}$

La partícula deja la pista, cuando la reacción N se anule, en los puntos tales que cumplen

${\displaystyle \begin{array}{l}mg\cos \theta =m\frac{v^2}{\rho }\\ g\left(1+{\left(\frac{dy}{dx}\right)}^2\right)=\left\{v_0^2+2g\left(y_0-y\right)\right\}\left|\frac{d^{2}y}{d{x}^2}\right|\end{array}}$

Analizaremos varias formas de pista, empezando por la más simple, la pista semicircular, estudiada en el primer apartado

Semicircular

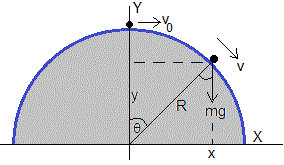
Sea una pista circular de radio R. La ecuación es x²+y²=R². Se lanza la partícula con velociad inicial v₀ desde el punto más alto y₀=R

${\displaystyle \begin{array}{l}\frac{dy}{dx}=\frac{-x}{\sqrt{R^2-x^2}}\\ \frac{d^{2}y}{d{x}^2}=-\frac{R^2}{{\left(R^2-x^2\right)}^{3/2}}\end{array}}$

La partícula se sale de la pista circular, cuando la reacción N se anule, en los puntos tales que cumplen

${\displaystyle \begin{array}{l}g\left(1+\frac{x^2}{R^2-x^2}\right)=\left\{v_0^2+2g\left(R-y\right)\right\}\frac{R^2}{{\left(R^2-x^2\right)}^{3/2}}\\ g=\left\{v_0^2+2g\left(R-y\right)\right\}\frac{1}{\sqrt{R^2-x^2}}\\ 3gy=v_0^2+2gR\\ \frac{y}{R}=\frac{2}{3}+\frac{v_0^2}{3gR}\end{array}}$

Si la velocidad inicial v₀=0, cosθ=y/R=2/3, resultado ya obtenido

El valor máximo de la velocidad inicial v₀ es aquél en el que cosθ=y/R=1, $v_0=\sqrt{gR}$

Elíptica

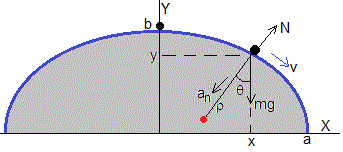
Cosideremos una pista de forma semielíptica de semejes a y b. La ecuación es

${\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$

Se proporciona una pequeña velocidad inicial v₀≈0, a la partícula en el punto más alto o posición de equilibrio inestable.

La ecuación del movimiento en la dirección normal a la pista en el punto (x,y) es

${\displaystyle mg\cos \theta -N=m\frac{v^2}{\rho }}$

• Calculamos la velocidad v en la posición (x,y) aplicando el principio de conservación de la energía

${\displaystyle \begin{array}{l}mgb=\frac{1}{2}m{v}^2+mgy\\ v^2=2g(b-y)\end{array}}$

• El radio de curvatura en el punto (x,y) de la pista vale

${\displaystyle \begin{array}{l}y=\frac{b}{a}\sqrt{a^2-x^2}\\ \frac{dy}{dx}=-\frac{b}{a}\frac{x}{\sqrt{a^2-x^2}}\\ \frac{d^{2}y}{d{x}^2}=-\frac{ab}{{\left(a^2-x^2\right)}^{3/2}}\\ \rho =\frac{{\left(a^4-\left(a^2-b^2\right)x^2\right)}^{3/2}}{a^{4}b}=\frac{{\left(b^4+\left(a^2-b^2\right)y^2\right)}^{3/2}}{a{b}^4}\end{array}}$

• Expresamos cosθ en terminos de la altura y

${\displaystyle \cos \theta =\frac{1}{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}=\frac{1}{\sqrt{1+\frac{b^2}{a^2}\frac{x^2}{a^2-x^2}}}=\frac{ay}{\sqrt{b^4+\left(a^2-b^2\right)y^2}}}$

Expresamos la reacción N en términos de la altura y del punto en la pista

${\displaystyle \begin{array}{l}N=mg\cos \theta -m\frac{v^2}{\rho }=\\ \frac{N}{mg}=\frac{ay}{\sqrt{b^4+\left(a^2-b^2\right)y^2}}-\frac{2(b-y)}{\frac{{\left(b^4+\left(a^2-b^2\right)y^2\right)}^{3/2}}{a{b}^4}}=\frac{a}{\sqrt{b^4+\left(a^2-b^2\right)y^2}}\left(y-\frac{2(b-y)b^4}{b^4+\left(a^2-b^2\right)y^2}\right)\end{array}}$

Representamos N/(mg) para b= 1 m y tres valores de el semeje a= 2, 1, 0.5 m

b=1; %semieje menor
hold on
for a=[2,1,0.5] %semieje mayor
    f=@(y) a*(y-2*(b-y)*b^4./(b^4+(a^2-b^2)*y.^2))./sqrt(b^4+(a^2-b^2)*y.^2);
    fplot(f,[0.5,1],'displayName',num2str(a))
end
hold off
xlabel('y')
ylabel('N/(mg)')
ylim([0,1])
grid on
legend('-DynamicLegend','location','best')
title('Reacción N de la cúpula')

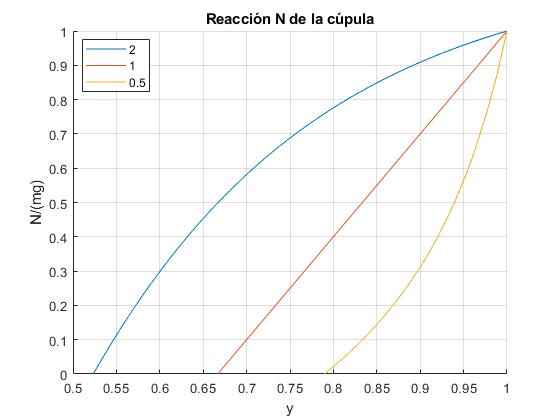
La reacción N se anula, la partícula deja de estar en contacto con la pista, a la altura y_c tal que

${\displaystyle \begin{array}{l}y-\frac{2(b-y)b^4}{b^4+\left(a^2-b^2\right)y^2}=0\\ \left(a^2-b^2\right)y^3+3b^{4}y-2b^5=0\end{array}}$

Utilizamos la función roots de MATLAB para calcular las raíces de la ecuación de tercer gardo. Alternativamente, se puede utilizar la función raices_3

>> a=2; b=1;
>> roots([a^2-b^2,0,3*b^4,-2*b^5])
ans =
  -0.2617 + 1.0979i
  -0.2617 - 1.0979i
   0.5233 + 0.0000i
>> a=1;
>> roots([a^2-b^2,0,3*b^4,-2*b^5])
ans =    0.6667

>> a=0.5;
>> roots([a^2-b^2,0,3*b^4,-2*b^5])
ans =
   -2.2743
    1.4845
    0.7899

• Cuando b=1 y a=2, y_c=0.5233 m
• Cuando b=1 y a=1, trayectoria semicircular, y_c=0.6667=2/3 m
• Cuando b=1 y a=0.5, y_c=0.7899 m

Forma de, Acos(kx)

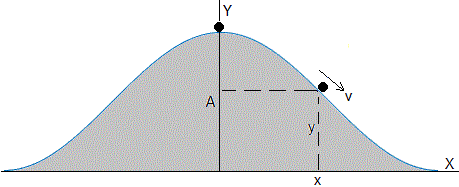
La pista responde a la ecuación y=Acos(kx) en el intervalo (-π/(2k), π/(2k)). Supongamos que la partícula parte del reposo, v₀=0, desde la cúspide a una altura y₀=A

${\displaystyle \begin{array}{l}\frac{dy}{dx}=-kA\sin (kx)\\ \frac{d^{2}y}{d{x}^2}=-k^{2}A\cos (kx)\end{array}}$

La partícula deja la pista, cuando la reacción N se anule, en los puntos tales que cumplen

${\displaystyle \begin{array}{l}1+k^2{A}^2{\sin }^2(kx)=2\left(A-A\cos (kx)\right)k^{2}A\cos (kx)\\ k^2{A}^2{\cos }^2(kx)-2k^2{A}^2\cos (kx)+1+k^2{A}^2=0\\ {\cos }^2(kx)-2\cos (kx)+\frac{1}{k^2{A}^2}+1=0\\ \cos (kx)=\frac{2\pm \sqrt{4-4\left(\frac{1}{k^2{A}^2}+1\right)}}{2}=1\pm i\frac{1}{kA}\end{array}}$

No hay raíces reales de la ecuación de segundo grado en cos(kx), por lo que la partícula desliza a lo largo de la pista

Parábola

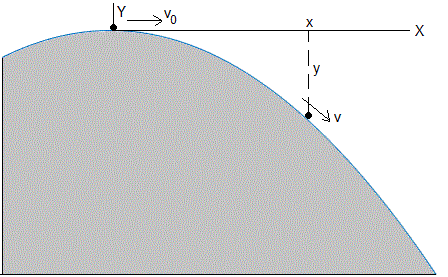
La pista es un tramo de parábola que responde a la ecuación, y=-αx². La partícula se lanza con velocidad inicial v₀ desde la altura y₀=0

${\displaystyle \begin{array}{l}\frac{dy}{dx}=-2\alpha x\\ \frac{d^{2}y}{d{x}^2}=-2\alpha \end{array}}$

La partícula se sale la pista, cuando la reacción N se anule, en los puntos tales que cumplen

${\displaystyle \begin{array}{l}g\left(1+4{\alpha }^2{x}^2\right)=\left\{v_0^2+2g\alpha x^2\right\}2\alpha \\ v_0^2=\frac{g}{2\alpha }\end{array}}$

Esta es la velocidad inicial crítica v_c que hace que N sea cero

Cuando la partícula se lanza con otra velocidad inicial v₀ distanta de v_c, la reacción N de la pista es

${\displaystyle \begin{array}{l}N=mg\cos \theta -m\frac{v^2}{\rho }=\frac{mg}{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}-m\frac{v_0^2+2g\left(0+\alpha x^2\right)}{\frac{{\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}^{3/2}}{\left|\frac{d^{2}y}{d{x}^2}\right|}}=\frac{mg}{\sqrt{1+4{\alpha }^2{x}^2}}-m\frac{v_0^2+2g\alpha x^2}{{\left(1+4{\alpha }^2{x}^2\right)}^{3/2}}2\alpha \\ N=\frac{mg}{\sqrt{1+4{\alpha }^2{x}^2}}\left(1-\frac{2\alpha \frac{v_0^2}{g}+4{\alpha }^2{x}^2}{1+4{\alpha }^2{x}^2}\right)\end{array}}$

Se presentan los siguientes casos:

• Si la velocidad inicial v₀ es igual a la crítica, $v_c=\sqrt{\frac{g}{2\alpha }}$

Comprobamos que N=0

• Si la velocidad inicial v₀ es mayor a la crítica

Comprobamos que N<0, la partícula abandona la pista desde el instante inicial

• Si la velocidad inicial v₀ es menor a la crítica

Comprobamos que N>0, la partícula desliza a lo largo de la pista

Referencias

I.S. Gradshteyn, I.M. Ryzhik. Table of Integrals, Series, and Products. Seventh Edition. Elsevier, 2007

Kirk T. McDonald. Skiing on a Cosine Hill. https://www.physics.princeton.edu/~mcdonald/examples/

Amir Aghamohammadi. The point of departure of a particle sliding on a curved surface. Eur. J. Phys. 33 (2012) pp. 1111–1117

R. S. Dutra, L. C. Ribeiro, C. M. Porto. Uma aplicação da dinâmica de uma partícula em uma trajetória predeterminada: o problema do iglu elipsoidal. Revista Brasileira de Ensino de Física, vol. 41, nº 2, e20180185 (2019)