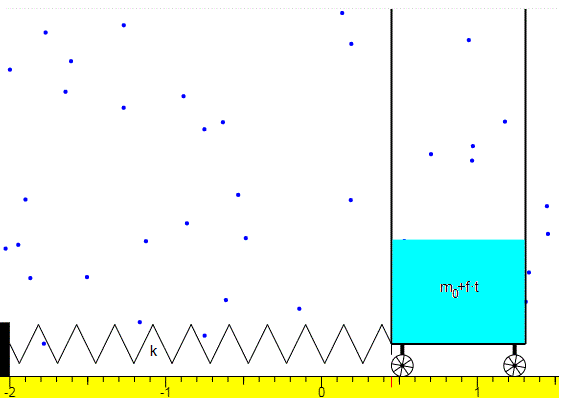
Supongamos que el vagón vacío de masa m₀ se conecta a un muelle elástico de constante k. En el instante t=0 se encuentra en el origen x=0 y se le proporciona una velocidad inicial v₀. A medida que la masa m del vagón se incrementa con el tiempo cabe esperar que la frecuencia de la oscilación del sistema formado por el muelle unido al vagón, ω²=k/m disminuya.

La frecuencia inicial de oscilación del sistema formado por un vagón vacío de masa m₀ unido a un muelle elástico de constante k es

${\displaystyle {\omega }_0^2=\frac{k}{m_0}}$

La ecuación del movimiento de un vagón de masa m=m₀+f·t unido a un muelle elástico de constante k es

${\displaystyle \begin{array}{l}\begin{array}{l}\frac{dp}{dt}=-kx\hfill \\ (m_0+f·t)\frac{dv}{dt}+fv=-kx\hfill \end{array}\\ (m_0+f·t)\frac{d^{2}x}{d{t}^2}+f\frac{dx}{dt}+m_0{\omega }_0^{2}x=0\end{array}}$

Hacemos el cambio de variable

${\displaystyle u=a\sqrt{1+\frac{f·t}{m_0}}a=\frac{2m_0{\omega }_0}{f}}$

Expresamos la derivada primera dx/dt en términos de dx/du

${\displaystyle \frac{dx}{dt}=\frac{dx}{du}\frac{du}{dt}=\frac{{\omega }_0}{\sqrt{1+\frac{f·t}{m_0}}}\frac{dx}{du}}$

Expresamos la derivada segunda d²x/dt² en términos de dx/du y de d²x/du²

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=\frac{d}{dt}\left(\frac{dx}{dt}\right)=\frac{d}{dt}\left(\frac{{\omega }_0}{\sqrt{1+\frac{f·t}{m_0}}}\frac{dx}{du}\right)=\\ -\frac{{\omega }_{0}f}{2m_0}{\left(1+\frac{f·t}{m_0}\right)}^{-3/2}\frac{dx}{du}+\frac{{\omega }_0}{\sqrt{1+\frac{f·t}{m_0}}}\frac{d}{dt}\left(\frac{dx}{du}\right)=\\ -\frac{{\omega }_{0}f}{2m_0}{\left(1+\frac{f·t}{m_0}\right)}^{-3/2}\frac{dx}{du}+\frac{{\omega }_0}{\sqrt{1+\frac{f·t}{m_0}}}\frac{d}{du}\left(\frac{dx}{du}\right)\frac{du}{dt}=\\ -\frac{{\omega }_{0}f}{2m_0}{\left(1+\frac{f·t}{m_0}\right)}^{-3/2}\frac{dx}{du}+\frac{{\omega }_0^2}{1+\frac{f·t}{m_0}}\frac{d^{2}x}{d{u}^2}\end{array}}$

Introducimos estas dos derivadas en la ecuación diferencial del movimiento

${\displaystyle \begin{array}{l}{m}_0\left(1+\frac{f·t}{m_0}\right)\left\{-\frac{{\omega }_{0}f}{2m_0}{\left(1+\frac{f·t}{m_0}\right)}^{-3/2}\frac{dx}{du}+\frac{{\omega }_0^2}{1+\frac{f·t}{m_0}}\frac{d^{2}x}{d{u}^2}\right\}+f\left\{\frac{{\omega }_0}{\sqrt{1+\frac{f·t}{m_0}}}\frac{dx}{du}\right\}+m_0{\omega }_0^{2}x=0\\ m_0{\omega }_0^2\frac{d^{2}x}{d{u}^2}+\frac{f{\omega }_0}{2\sqrt{1+\frac{f·t}{m_0}}}\frac{dx}{du}+m_0{\omega }_0^{2}x=0\\ \frac{d^{2}x}{d{u}^2}+\frac{1}{u}\frac{dx}{du}+x=0\end{array}}$

La solución de esta ecuación diferencial es una combinación lineal de las funciones de Bessel J₀(u) y Y₀(u).

${\displaystyle x=A{J}_0(u)+B{Y}_0(u)}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales: en el instante t=0, en vagón se encuentra en el origen x=0, con velocidad inicial v=v₀

Para calcular la velocidad dx/dt tenemos en cuenta las derivadas de las funciones de Bessel

${\displaystyle \begin{array}{l}\frac{d}{du}{J}_0(u)=-J_1(u)\\ \frac{d}{du}{Y}_0(u)=-Y_1(u)\end{array}}$

>> syms x;
>> diff(besselj(0,x))
 ans =-besselj(1, x)
 
>> diff(bessely(0,x))
 ans =-bessely(1, x)

${\displaystyle \begin{array}{l}\frac{dx}{dt}=-\left(A{J}_1(u)+B{Y}_1(u)\right)\frac{du}{dt}\\ \frac{dx}{dt}=-\left(A{J}_1(u)+B{Y}_1(u)\right)\frac{af}{2m_0\sqrt{1+f·t/m_0}}=-\frac{a^{2}f}{2m_0}\frac{1}{u}\left(A{J}_1(u)+B{Y}_1(u)\right)\end{array}}$

Teniendo en cuenta que para t=0, u=a, calculamos los coeficientes A y B a partir de las condiciones iniciales

${\displaystyle \begin{array}{l}\{\begin{array}{l}0=A{J}_0(a)+B{Y}_0(a)\\ v_0=-\frac{af}{2m_0}\left(A{J}_1(a)+B{Y}_1(a)\right)\end{array}\\ A=-\frac{v_0}{{\omega }_0}\frac{Y_0(a)}{J_1(a)Y_0(a)-J_0(a)Y_1(a)}\\ B=\frac{v_0}{{\omega }_0}\frac{J_0(a)}{J_1(a)Y_0(a)-J_0(a)Y_1(a)}\end{array}}$

La posición x y la velocidad v del vagón son

${\displaystyle \begin{array}{l}x=\frac{v_0}{{\omega }_0}\frac{J_0(a)Y_0(u)-Y_0(a)J_0(u)}{J_1(a)Y_0(a)-J_0(a)Y_1(a)}\\ v=a{v}_0\frac{1}{u}\frac{Y_0(a)J_1(u)-J_0(a)Y_1(u)}{J_1(a)Y_0(a)-J_0(a)Y_1(a)}\end{array}}$

Sea

• f=0.7 kg/s
• v₀=1 m/s
• m₀=50 kg
• Frecuencia angular inicial t=0, ω₀=1 rad/s

m0=50; %Masa del depósito vacío
f=0.7;  %Flujo
v0=1;  %Velocidad inicial del depósito
w0=1; %frecuencia angular inicial
a=2*m0*w0/f;
den=besselj(1,a)*bessely(0,a)-besselj(0,a)*bessely(1,a);

subplot(2,1,1);
v=@(t) a*v0*(bessely(0,a)*besselj(1,a*sqrt(1+f*t/m0))-besselj(0,a)
*bessely(1,a*sqrt(1+f*t/m0)))./(den*a*sqrt(1+f*t/m0));
fplot(v,[0,50])
grid on
xlabel('t(s)')
ylabel('v(m/s)')
title('Velocidad')

subplot(2,1,2);
x=@(t) v0*(besselj(0,a)*bessely(0,a*sqrt(1+f*t/m0))-bessely(0,a)*
besselj(0,a*sqrt(1+f*t/m0)))/(den*w0);
fplot(x,[0,50])
grid on
xlabel('t(s)')
ylabel('x(m)')
title('Posición')

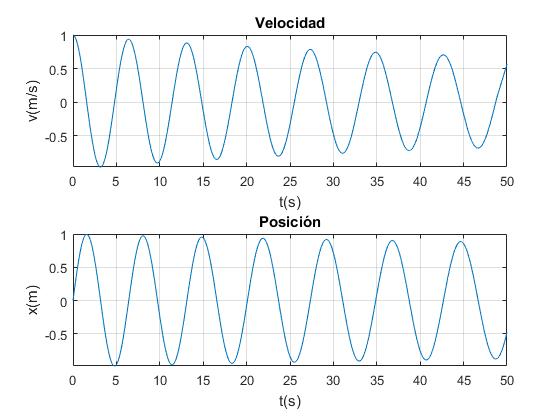
A medida que aumenta la masa m del vagón, la frecuencia angular ω²=k/m disminuye, el periodo aumenta, tal como observamos en al figura

Actividades

Se introduce

• La velocidad inicial v₀, en el control titulado Velocidad inicial

• La masa inicial del vagón se ha fijado en m₀=50 kg

• La razón constante f del incremento de la masa del vagón, en el control titulado Flujo

• Se ha fijado el valor de la constante del muelle o la frecuencia angular inicial ω₀=1 rad/s

Se pulsa el botón titulado Nuevo.

Se observa el movimiento oscilatorio del vagón.

La masa del vagón se incrementa con el tiempo, debido a la caída de la lluvia, que se representa por el movimiento vertical de puntos de color azul.

Referencias

Lapidus I. R. Problem: the rain in the plain falls mainly on the train. Am. J. Phys. 53 (7) July 1985, Enunciado pág 644, solución pág 697.