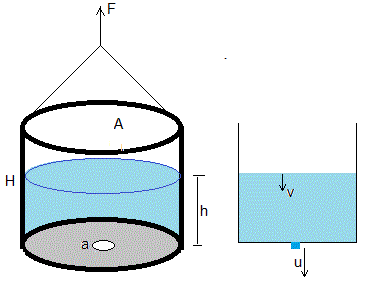
Un recipiente de sección A se llena de líquido de densidad ρ hasta una altura H.

En el instante t=0, se abre un pequeño orificio de sección a<<A situado en el fondo del recipiente. Como consecuencia la altura h del nivel de líquido disminuye con el tiempo hasta que el recipiente se vacía. La ley de Torricelli nos dice que la velocidad de salida del líquido por el pequeño orificio es

${\displaystyle u=\sqrt{2gh}}$

Por la ecuación de continuidad

${\displaystyle au=Av,v=-\frac{dh}{dt}}$

El nivel de líquido h decrece con el tiempo, la velocidad v con la que decrece es

${\displaystyle \frac{dh}{dt}=-\frac{a}{A}\sqrt{2gh}}$

Integramos esta ecuación diferencial con la condición inicial en el instante t=0, el nivel de líquido es H. Separando variables.

${\displaystyle \begin{array}{l}{\displaystyle \underset{H}{\overset{h}{\int }}\frac{dh}{\sqrt{h}}}=-\frac{a}{A}\sqrt{2g}{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ 2\left(\sqrt{h}-\sqrt{H}\right)=-\frac{a}{A}\sqrt{2g}·t\\ \sqrt{h}=\sqrt{H}-\frac{1}{2}\frac{a}{A}\sqrt{2g}·t\\ h={\left(\sqrt{H}-\frac{1}{2}\frac{a}{A}\sqrt{2g}·t\right)}^2\end{array}}$

El recipiente se vacía h=0 en el instante

${\displaystyle T=\frac{A}{a}\sqrt{\frac{2H}{g}}}$

Sea un recipiente cilíndrico de 17 mm de diámetro que contiene líquido hasta una altura H=1.655 m

Vamos a representar la altura h de la superficie libre del líquido en función del tiempo t para tres diámetros del orificio situado en el fondo, 4, 7 y 10 mm

d1=17/1000; %diámetro del recipiente
H=1.655; %altura inicial
hold on
for d2=[4,7,10]/1000 %diámetros orificio
    h=@(t) (sqrt(H)-d2^2*sqrt(2*9.8)*t/(2*d1^2)).^2;
    T=sqrt(2*H/9.8)*d1^2/d2^2; %tiempo vaciado
    fplot(h,[0,T],'displayName',num2str(d2*1000))
end
hold off
grid on
legend('-DynamicLegend','location','best')
xlabel('t (s)')
ylabel('h (m)')
title('Altura del nivel de líquido')

Fuerza de empuje

Colgamos de una balanza un recipiente cilíndrico vacío de seción A y taramos a cero. Lo llenamos de líquido de densidad ρ hasta una altura H. La balanza mide el peso del líquido (ρAH)g en el instante t=0

Abrimos un pequeño orificio de sección a situado en el fondo. En el instante t, la fuerza F que mide la balanza no es el peso del líquido de altura h, (ρAh)g, es algo menor

Hay que tener en cuenta la fuerza de empuje que proporciona al líquido que sale del recipiente con velocidad u, similar a un cohete.

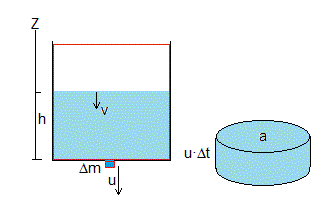
La fuerza externa que actúa sobre el recipiente que contiene líquido hasta una altura h

${\displaystyle \overrightarrow{F_{ext}}=\left(-\left(\rho gh\right)+F\right)\widehat{k}}$

(ρAh)g es el peso del líquido contenido en el recipiente y F es la fuerza que mide la balanza

La fuerza externa cambia el momento lineal del sistema formado por el líquido contenido en el recipiente y el líquido que sale por el orificio situado en el fondo

• Sea Δp₁ es el momento lineal del líquido que sale por el orificio en el intervalo de tiempo comprendido entre t y t+Δt

${\displaystyle \overrightarrow{\Delta p_1}=\Delta m\overrightarrow{u}=\Delta m\left(-u\right)\widehat{k}=\left(\rho a·u·\Delta t\right)\left(-u\right)\widehat{k}=-\rho a·u^2·\Delta t\widehat{k}}$

En el límite cuando Δt→0

${\displaystyle \frac{d\overrightarrow{p_1}}{dt}=-\rho a·u^2\widehat{k}}$

• Sea p₂ el momento lineal del líquido contenido en el recipiente

${\displaystyle \begin{array}{l}\overrightarrow{p_2}=\left(\rho Ah\right)\overrightarrow{v}=-\left(\rho Ah\right)v\widehat{k}=-\rho hau\widehat{k}=-\rho ha\sqrt{2gh}\widehat{k}=-\rho a\sqrt{2g}·h^{3/2}\widehat{k}\\ \frac{d\overrightarrow{p_2}}{dt}=-\rho a\sqrt{2g}\frac{3}{2}\sqrt{h}\frac{dh}{dt}\widehat{k}=-\rho a\sqrt{2g}\frac{3}{2}\sqrt{h}\left(-\frac{a}{A}\sqrt{2gh}\right)\widehat{k}=\frac{3}{2}\rho \frac{a^2}{A}{u}^2\widehat{k}\end{array}}$

La fuerza externa es la suma de las dos contribuciones

${\displaystyle \overrightarrow{F_{ext}}=\frac{d\overrightarrow{p_1}}{dt}+\frac{d\overrightarrow{p_2}}{dt}=-\rho a·u^2\widehat{k}+\frac{3}{2}\rho \frac{a^2}{A}{u}^2\widehat{k}=-\rho a\left(1-\frac{3}{2}\frac{a}{A}\right)\left(2gh\right)\widehat{k}}$

La fuerza F que mide la balanza es

${\displaystyle \begin{array}{l}\overrightarrow{F_{ext}}=\left(-\left(\rho gh\right)+F\right)\widehat{k}\\ -\rho a\left(1-\frac{3}{2}\frac{a}{A}\right)\left(2gh\right)\widehat{k}=\left(-\left(\rho gh\right)+F\right)\widehat{k}\\ F=\left(\rho gh\right)\left(1-2a\left(1-\frac{3}{2}\frac{a}{A}\right)\right)\end{array}}$

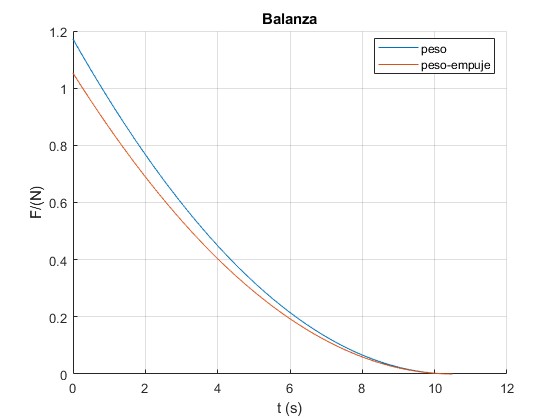
Vamos a representar la fuerza F que ejerce la balanza y el peso del agua (densidad ρ=1000 kg/m³) contenida en el recipente, (ρAh)g en función del tiempo t para un orificio de 4 mm de diámetro. La altura inicial de líquido es H=1.655 m

d1=17/1000; %diámetro del recipiente
H=1.655; %altura inicial
hold on
d2=4/1000; %diámetro del orificio
T=sqrt(2*H/9.8)*d1^2/d2^2; %tiempo de vaciado
h=@(t) (sqrt(H)-d2^2*sqrt(2*9.8)*t/(2*d1^2)).^2; %altura nivel
E=@(t) 2*9800*(d2^2/4)*h(t)*(1-3*d2^2/(2*d1^2)); %empuje
M=@(t) 9800*(d1^2/4)*h(t); %peso
F=@(t) M(t)-E(t); %mide la balanza
fplot(M,[0,T])
fplot(F,[0,T])
hold off
grid on
legend('peso', 'peso-empuje','location','best')
xlabel('t (s)')
ylabel('F/(N)')
title('Balanza')

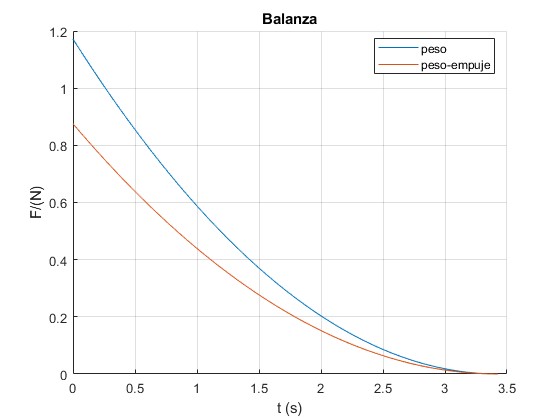
Cambiamos el diámetro del orificio a 7 mm en la variable d2

Referencias

Avi Marchewka, Yiftah Navot. The recoil force on a leaking water tank. Eur. J. Phys. 46 (2025) 035804