Consideremos una cadena delgada, idealmente flexible, de densidad ρ que está apilada en el suelo. Estudiaremos el movimiento de un extremo de la cadena cuando se le aplica una fuerza constante F. Dicha fuerza sería igual a la diferencia entre el empuje y el peso del globo atado a su extremo.

Situando el origen en el suelo, la posición del extremo de la cadena es x>0. Supondremos que en determinado instante t, hay una parte de la cadena x en movimiento con velocidad v y la otra parte, en reposo sobre el suelo.

Equilibrio

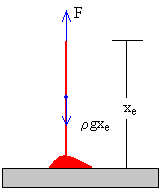
La cadena está en equilibrio, cuando la fuerza aplicada F es igual al peso de la parte de la cadena que cuelga x_e.

F=ρgx_e

Cuando el extremo de la cadena está a una altura x₀<x_e y se suelta, vamos a estudiar el movimiento hacia arriba y hacia abajo de dicho extremo.

Movimiento hacia arriba (v>0)

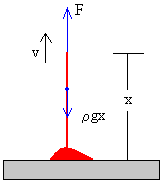
La derivada del momento lineal p, de la parte de la cadena que se mueve, con respecto al tiempo t, es igual a la fuerza resultante

${\displaystyle \frac{dp}{dt}=F-\rho gx}$

donde p es el momento lineal p=(ρx)·v

${\displaystyle x\frac{dv}{dt}+v^2=\frac{F}{\rho }-gx\frac{d^{2}x}{d{t}^2}=\frac{F}{\rho x}-g-\frac{1}{x}{\left(\frac{dx}{dt}\right)}^2}$

Se resuelve esta ecuación diferencial por procedimientos numéricos con las condiciones iniciales t=0, x=x₀, v=dx/dt=0.

• Cuando x<x_e, el extremo de la cadena incrementa su velocidad hacia arriba, ya que la fuerza aplicada F es mayor que el peso ρgx.

• Cuando x>x_e, el extremo de la cadena disminuye su velocidad ya que la fuerza aplicada F es menor que el peso ρgx.

• Cuando la velocidad final se haga cero, (posición de retorno x₁) el movimiento hacia arriba cesa y el extremo de la cadena inicia su movimiento hacia abajo.

Cálculo de la posición de retorno x₁.

Escribiendo la ecuación diferencial del movimiento de la forma

${\displaystyle \frac{d(xv)}{dt}=\frac{F}{\rho }-gx}$

Teniendo en cuenta que $\frac{dy}{dt}=\frac{dy}{dx}·\frac{dx}{dt}$

${\displaystyle v\frac{d(xv)}{dx}=\frac{F}{\rho }-gx(xv)\frac{d(xv)}{dx}=\frac{Fx}{\rho }-g{x}^2}$

Integramos

${\displaystyle \begin{array}{l}{\displaystyle \underset{x_0,v_0}{\overset{x,v}{\int }}(xv)d(xv)}={\displaystyle \underset{x_0}{\overset{x}{\int }}\left(\frac{F}{\rho }x-g{x}^2\right)dx}\\ \frac{1}{2}{\left(xv\right)}^2-\frac{1}{2}{\left(x_0{v}_0\right)}^2=\frac{1}{2}\frac{F}{\rho }{x}^2-\frac{1}{3}g{x}^3-\frac{1}{2}\frac{F}{\rho }{x}_0^2+\frac{1}{3}g{x}_0^3\end{array}}$

Como la velocidad inicial v₀=0, y la velocidad final en la posición de retorno x=x₁ es igualmente nula v=0, llegamos a la ecuación cúbica

${\displaystyle \frac{g}{3}{x}^3-\frac{F}{2\rho }{x}^2+\frac{F}{2\rho }{x}_0^2-\frac{g}{3}{x}_0^3=0}$

Una de cuyas raíces es x₀, la posición de partida.

${\displaystyle (x-x_0)\left(\frac{g}{3}{x}^2+\left(\frac{g}{3}{x}_0-\frac{F}{2\rho }\right)x+\frac{g}{3}{x}_0^2-\frac{F}{2\rho }{x}_0\right)=0}$

La raíz positiva x₁ de la ecuación de segundo grado es

${\displaystyle \begin{array}{l}x=-\left(\frac{x_0}{2}-\frac{3F}{4\rho g}\right)\pm \sqrt{-\frac{3x_0^2}{4}+\frac{9F^2}{16{\rho }^2{g}^2}+\frac{3F{x}_0}{4\rho g}}\\ x_1=\frac{1}{2}\left(\frac{3}{2}{x}_e-x_0\right)+\frac{1}{2}\sqrt{-3x_0^2+\frac{9}{4}{x}_e^2+3x_e{x}_0}\end{array}}$

donde x_e=F/(ρg) es la posición de equilibrio.

Movimiento hacia abajo (v<0)

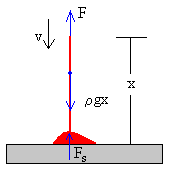
En el caso del movimiento hacia abajo, la situación es diferente. En un intervalo de tiempo dt, una masa dm de la cadena cuya velocidad es v, choca inelásticamente contra el suelo y se detiene completamente. Esta disminución de momento lineal v·dm de la cadena en el tiempo dt, se debe a su interacción con el suelo, que podemos describir mediante una fuerza hacia arriba F_s= vdm/dt=ρv²

Una explicación más completa se encuentra al final de la página titulada Movimiento de una cadena con una máquina de Atwood

La derivada del momento lineal p de la parte de la cadena que se mueve con respecto al tiempo t es igual a la fuerza resultante

${\displaystyle \begin{array}{l}\frac{dp}{dt}=F-\rho gx+F_{s}v\frac{dm}{dt}+m\frac{dv}{dt}=F-\rho gx+v\frac{dm}{dt}\\ \rho x\frac{dv}{dt}=F-\rho gx\end{array}}$

Se resuelve la ecuación diferencial por procedimientos numéricos

${\displaystyle \frac{d^{2}x}{d{t}^2}=\frac{F}{\rho x}-g}$

con las condiciones iniciales siguientes: en el instante t₁, x=x₁, v=dx/dt=0.

• Cuando x>x_e, el extremo de la cadena incrementa su velocidad hacia abajo, ya que el peso ρgx es mayor que la fuerza aplicada F.

• Cuando x<x_e, el extremo de la cadena disminuye su velocidad ya que la fuerza aplicada F es mayor que el peso ρgx.

• Cuando la velocidad final se haga cero, (posición de retorno x₂) el movimiento hacia abajo cesa y el extremo de la cadena inicia su movimiento hacia arriba.

Caso particular.

Cuando la fuerza F=0, la cadena cae libremente. La velocidad de caída del extremo libre es v=-g·t. La fuerza que ejerce el suelo para parar los eslabones que caen es

${\displaystyle F_s=v\frac{dm}{dt}=\rho v^2=\rho {\left(gt\right)}^2}$

Suponemos que v=0, cuando x=L, siendo L la longitud de la cadena. En el instante t, la altura del último eslabón de la cadena es x, una longitud L-x se encuentra en reposo sobre el suelo.

La reacción N del suelo es la suma de dos términos:

• la fuerza F_s que ejerce el suelo para parar los eslabones de la cadena que caen

• el peso de la porción (L-x) de cadena que ya está en reposo sobre el suelo

${\displaystyle \begin{array}{l}x=L+\frac{1}{2}(-g)t^2\\ N=2\frac{M}{L}g(L-x)+\frac{M}{L}g(L-x)=3\frac{M}{L}g(L-x)\end{array}}$

Siendo M=ρL la masa de la cadena.

Cuando llega el último eslabón de la cadena al  suelo x=0.

N=3Mg

Si dejamos caer la cadena sobre el plato de una balanza, ésta medirá una fuerza máxima 3Mg.

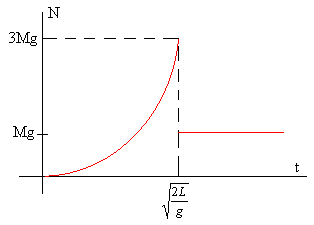
Resumiendo: cuando la cadena está completamente levantada con el primer eslabón tocando el plato de la balanza, ésta mide una fuerza nula. Cuando el último eslabón cae sobre el plato, la balanza mide una fuerza máxima igual a tres veces el peso de la cadena. Finalmente, la balanza mide una fuerza igual al peso de la cadena.

Cálculo de la posición de retorno x₂.

Escribimos la ecuación diferencial del movimiento de la forma

${\displaystyle \frac{dv}{dt}=\frac{F}{\rho x}-gv\frac{dv}{dx}=\frac{F}{\rho x}-g}$

Integramos

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{v}{\int }}vdv}={\displaystyle \underset{x_1}{\overset{x}{\int }}\left(\frac{F}{\rho x}-g\right)dx}\\ \frac{1}{2}{v}^2=\frac{F}{\rho }\ln x-gx-\left(\frac{F}{\rho }\ln x_1-g{x}_1\right)\end{array}}$

En la posición de retorno x₂, la velocidad del extremo de la cadena es v=0.

${\displaystyle x_e\ln \left(\frac{x_1}{x_2}\right)=x_1-x_2}$

donde $x_e=\frac{F}{\rho g}$ es la posición de equilibrio.

Conocido x₁ se calcula x₂, resolviendo la ecuación trascendente por procedimientos numéricos.

La posición de retorno x₂ es ahora la posición de partida x₀ para el movimiento hacia arriba y así, sucesivamente.

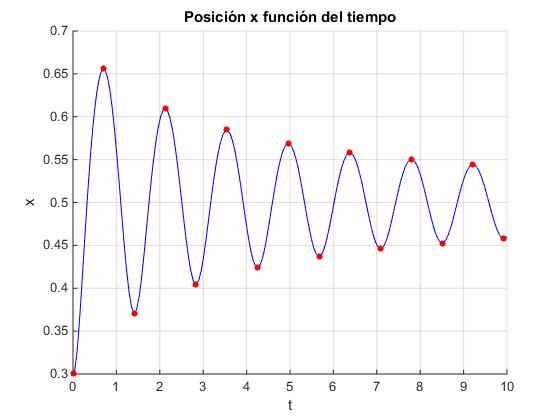
El extremo de la cadena describe una oscilación amortiguada. Al cabo de un cierto tiempo teóricamente infinito, el extremo de la cadena se encuentra en la posición de equilibrio x_e.

Cálculo con MATLAB

Posiciones de retorno

Calculamos las primeras posiciones de retorno. Aquellas en las que la velocidad v=0

xe=0.5; %altura de equilibrio
xAbajo=0.3; %altura inicial menor que la de equilibrio

x0=xAbajo;
for i=1:10
    %movimiento hacia arriba
    xArriba=(3*xe/2-x0)/2+sqrt(-3*x0^2+9*xe^2/4+3*xe*x0)/2;
    x0=xArriba;
    disp([xAbajo xArriba])
    %movimiento hacia abajo
    f=@(x) xe*log(x0/x)-x0+x; 
    xAbajo=fzero(f,[xAbajo xe]);
    x0=xAbajo;
end

    0.3000    0.6558
    0.3710    0.6096
    0.4044    0.5847
    0.4239    0.5690
    0.4368    0.5582
    0.4460    0.5504
    0.4528    0.5444
    0.4581    0.5397
    0.4623    0.5359
    0.4657    0.5328

La sucesión converge hacia la posición de equilibrio x_e=0.5

Posición en función del tiempo

Resolvemos las dos ecuaciones diferenciales de segundo orden: la primera describe el movimiento de la cadena hacia arriba y la segunda hacia abajo

function z = mov_cadenaGlobo(~,x,xe)
    %x(1) es x
    %x(2) es v
    z=zeros(2,1);
    z(1)=x(2);
    if x(2)>0 %hacia arriba (velocidad positiva)
		z(2)=9.8*(xe/x(1)-1-x(2)^2/(9.8*x(1)));
    else %hacia abajo (velocidad negativa)
		z(2)=9.8*(xe/x(1)-1);
    end
 end

xe=0.5; %altura de equilibrio
opts=odeset('events',@parabola_ode45);
f=@(t,x) mov_cadenaGlobo(t,x,xe);
[t,x,te,xe,ie]=ode45(f,[0,10],[0.3,0],opts);

hold on
plot(t,x(:,1),'b')
plot(te(ie==1),xe(ie==1),'ro','markersize',4,'markerfacecolor','r')
hold off
grid on
xlabel('t')
ylabel('x');
title('Posición x función del tiempo')

Para marcar las posiciones de retorno definimos la función, que ya se ha utilizado en Movimiento sobre una superficie parabólica

function [detect,stopin,direction]=parabola_ode45(~,x)
    detect=x(2); 
    stopin=0;
    direction=0; 
end

Actividades

Se introduce

• La posición inicial del extremo de la cadena x₀<x_e, en el control titulado Altura inicial.

• La altura de equilibrio se ha fijado en x_e=0.5 m

Se pulsa el botón titulado Nuevo.

Se observa el movimiento del extremo de la cadena hacia arriba y hacia abajo

Se representan las fuerzas sobre la cadena:

• El peso de la parte de la cadena que se mueve

• La fuerza F aplicada

• En el movimiento hacia abajo, la fuerza que ejerce el suelo sobre la cadena F_s es pequeña en comparación con las otras dos.

Se representa las posiciones de retorno x₀, x₁, x₂,… en una regla situada a la izquierda.

Se representa la altura x del extremo de la cadena en función del tiempo t.

Se dispara una flecha atada a una cuerda muy larga

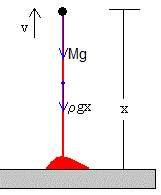
Se dispara verticalmente, una flecha de masa M atada a una cuerda muy larga de densidad ρ. Supondremos que no hay rozamiento

La fuerza F es el peso Mg de la flecha y apunta hacia abajo. La ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{dp}{dt}=-Mg-\rho gx\\ p=(M+\rho x)v\end{array}}$

donde p es el momento lineal de la flecha y de la parte x de cuerda que se mueven con velocidad v=dx/dt.

Velocidad en función de la altura

Expresamos la velocidad v en función de la posición x de la flecha teniendo en cuenta que

${\displaystyle \frac{dp}{dt}=\frac{dp}{dx}\frac{dx}{dt}=v\frac{dp}{dx}=\frac{p}{M+\rho x}\frac{dp}{dx}}$

La ecuación del movimiento se escribe

${\displaystyle \begin{array}{l}\frac{p}{M+\rho x}\frac{dp}{dx}=-Mg-\rho gx\\ \frac{p·dp}{dx}=-{\left(M+\rho x\right)}^{2}g\end{array}}$

Integrando entre la posición inicial x=0 y la final x

${\displaystyle {\displaystyle \underset{p_0}{\overset{p}{\int }}p·dp}={\displaystyle \underset{0}{\overset{x}{\int }}-g{\left(M+\rho x\right)}^{2}dx}}$

Haciendo el cambio de variable u=M+ρx, du=ρ·dx

${\displaystyle \begin{array}{l}\frac{1}{2}{p}^2-\frac{1}{2}{p}_0^2=-\frac{g}{\rho }{\displaystyle \underset{u_0}{\overset{u}{\int }}{u}^{2}du}\\ \frac{1}{2}{\left(M+\rho x\right)}^2{v}^2-\frac{1}{2}{M}^2{v}_0^2=-\frac{g}{3\rho }\left(u^3-u_0^3\right)\\ u^2{v}^2-M^2{v}_0^2=-\frac{2g}{3\rho }\left(u^3-M^3\right)\end{array}}$

Despejamos la velocidad v

${\displaystyle \begin{array}{l}v=\frac{1}{u}\sqrt{M^2{v}_0^2+\frac{2g}{3\rho }{M}^3-\frac{2g}{3\rho }{u}^3}\\ v=\frac{1}{\left(1+\frac{\rho x}{M}\right)}\sqrt{v_0^2-\frac{2Mg}{3\rho }\left({\left(1+\frac{\rho x}{M}\right)}^3-1\right)}\end{array}}$

Altura máxima

La altura máxima se alcanza cuando la velocidad v=0

${\displaystyle \begin{array}{l}{M}^2{v}_0^2=\frac{2g}{3\rho }\left(u_m^3-M^3\right)\\ u_m=M{\left(\frac{3\rho }{2Mg}{v}_0^2+1\right)}^{1/3}\\ x_m=\frac{u_m-M}{\rho }=\frac{M}{\rho }\left\{{\left(\frac{3\rho }{2Mg}{v}_0^2+1\right)}^{1/3}-1\right\}\end{array}}$

Cuando se dispara la flecha verticalmente sin cuerda, alcanza una altura máxima mayor

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}_0^2=mg{x}_m\\ x_m=\frac{v_0^2}{2g}\end{array}}$

Se obtiene de la fórmula x_m en el límite, cuando ρ→0.

${\displaystyle \underset{\rho \to 0}{\lim }\left(\frac{M}{\rho }\left\{{\left(\frac{3\rho }{2Mg}{v}_0^2+1\right)}^{1/3}-1\right\}\right)=\frac{1}{3}\left(\frac{3}{2g}{v}_0^2\right)=\frac{v_0^2}{2g}}$

Llamando, $a=\frac{3}{2g}{v}_0^2,x=\frac{\rho }{M}$

>> syms a x;
>> limit(((a*x+1)^(1/3)-1)/x,x,0)
ans =a/3

Representamos la velocidad de una flecha de masa M=10 kg que se dispara verticalmente con velocidad inicial v₀=30 m/s, atada a una cuerda muy larga de densidad ρ=0.1 kg/m

M=10; %kg, masa flecha
rho=0.1; % kg/m densidad lineal
v0=30; % m/s, velocidad inicial
f=@(x) sqrt(v0^2-2*M*9.8*((1+rho*x/M).^3-1)/(3*rho))./(1+rho*x/M);
xm=M*((3*rho*v0^2/(2*M*9.8)+1)^(1/3)-1)/rho; %altura máxima
hold on
fplot(f,[0,xm]) %con cuerda
fplot(@(x) sqrt(v0^2-2*9.8*x),[0, v0^2/(2*9.8)]) %sin cuerda
hold off
grid on
xlabel('x (m)')
ylabel('v (m/s)');
legend('con cuerda','sin cuerda', 'Location','best')
title('Movimiento de la flecha')

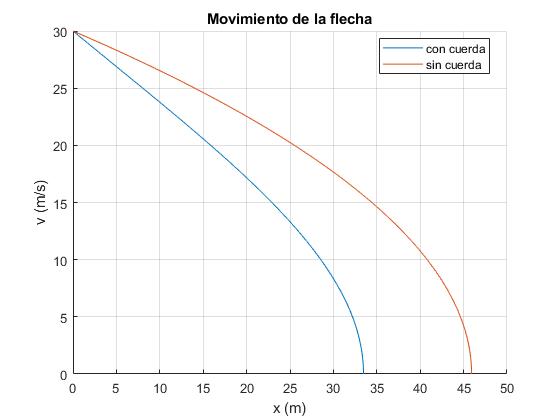
La altura máxima es

>> xm
xm =   33.4678
>> v0^2/(2*9.8)
ans =   45.9184

Ecuación del movimiento

La ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}(M+\rho x)v=-Mg-\rho gx\\ (M+\rho x)\frac{d^{2}x}{d{t}^2}+\rho {\left(\frac{dx}{dt}\right)}^2+\rho gx+Mg=0\end{array}}$

Resolvemos la ecuación del movimiento por el procedimiento numérico ode45 de MATLAB, con las siguientes condiciones iniciales: en el instante t=0, la flecha parte del origen x=0, con velocidad dx/dt=v₀

El procedimiento numérico se interrumpe cuando se alcanza la altura máxima dx/dt=0

function flecha
    M=10; %kg, masa flecha
    rho=0.1; % kg/m densidad lineal
    v0=30; % m/s, velocidad inicial
    opts=odeset('events',@flecha_ode45);
    f=@(t,x)[x(2); -(rho*x(2)^2+(rho*x(1)+M)*9.8)/(M+rho*x(1))];
    [t,x]=ode45(f,[0,5],[0,v0], opts);
    hold on
    plot(t,x(:,1)) %con cuerda
    fplot(@(t) v0*t-4.9*t.^2,[0,v0/9.8]) %sin cuerda
    hold off
    grid on
    xlabel('t (s)')
    ylabel('x (m)');
    legend('con cuerda','sin cuerda', 'Location','best')
    title('Movimiento de la flecha')
    disp([t(end),x(end,1)])

    function [detect,stopin,direction]=flecha_ode45(~,x)
        detect=x(2); 
        stopin=1;
        direction=-1; 
    end
end

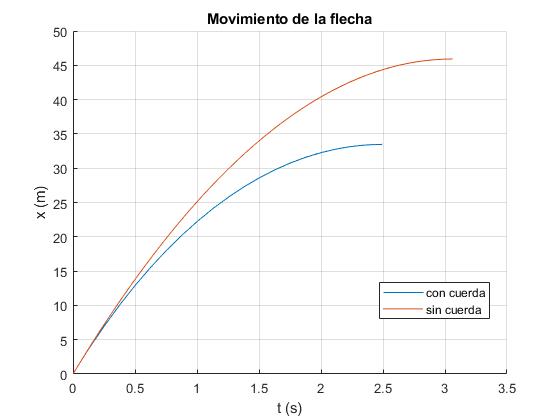
La altura máxima es x_m=33.4679 m, y el tiempo que tarda en alcanzarla es t_m=2.4937 s

    2.4937   33.4679

Referencias

Sima V., Podolsky J., Buquoy's problem. Eur. J. Phys. 26 (2005) pp. 1037-1045

van den Berg W. H. Force exerted by a falling chain. The Physics Teacher, 36, January 1998, pp. 44-45

Carl E. Mungan, Trevor C. Lipscombe. Vertical Launch of a Grappling Hook. The Physics Teacher, Vol. 60, May 2022. pp. 327-330