El “cohete” de Torricelli
Vaciado del depósito
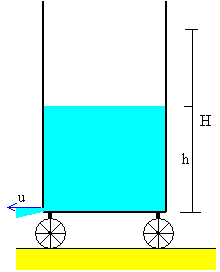
En el capítulo Fluidos, se estudia el vaciado de un depósito de sección S1=πR2 que se ha llenado de agua hasta una altura H. Si se abre un orificio de área S2= πr2 en el fondo. La velocidad u de salida del agua cuando su superficie libre está a una altura h sobre el fondo, de acuerdo al teorema de Torricelli es
Un análisis más detallado que tenga en cuenta las dimensiones del depósito (de sección S1) y del orificio (sección S2) con conduce a la expresión
Consideramos g’ como una aceleración de la gravedad efectiva, que coincide con g si el radio del orificio r es mucho menor que el radio R del depósito.
A medida que el agua, de densidad ρ, sale por el orificio, la altura h o la masa m=ρπR2h de agua en el depósito va disminuyendo con el tiempo. Como el gasto o volumen del fluido que sale por el orificio en la unidad de tiempo es πr2u, La masa m de agua disminuye de acuerdo con la ecuación
Integramos esta ecuación diferencial entre el instante t=0, en el que la masa de agua es m0= ρπR2H, y el instante t en el que la masa de agua es m.
Finalmente, nos queda
El depósito se vacía completamente en el instante tmáx, en el que la altura h, o la masa m de agua es cero
Movimiento del depósito
La definición de fuerza es
El sistema formado por el depósito y el agua es aislado, por lo que la fuerza F=0.
Al estudiar el movimiento de un cohete de empuje constante, deducimos la ecuación del movimiento
donde u era la velocidad de salida de los gases respecto de cohete y m la masa total del cohete (recipiente vacío y combustible).
En este caso, separamos la masa total en dos partes: la masa m de agua que va disminuyendo y la masa constante M del depósito vacío y la plataforma sobre la que descansa el depósito.
En función del tiempo t, la ecuación del movimiento se escribe
Integramos esta ecuación entre el instante t=0, en el que la velocidad del depósito es v=0, y el instante t, en el que la velocidad es v. Haciendo el cambio de variable
tenemos que integrar
Deshaciendo el cambio, obtenemos la expresión de la velocidad v en función del tiempo t.
Integrando con respecto del tiempo obtenemos la posición x de la plataforma en función del tiempo t. Para ello necesitamos la integral del arco tangente.
Se ha agotado el agua almacenada en el depósito en el instante tmax tal que
La velocidad máxima es
y se produce cuando el depósito se encuentra en la posición x.
En un cohete, la velocidad final no depende de la cantidad de combustible D que se quema por segundo, sino de la masa inicial, de la masa final y de la velocidad constante u de salida de los gases respecto del cohete.
La velocidad final de este cohete peculiar que estudiamos en esta página, depende a través de g' del radio r del orificio de salida del agua, es decir, de la cantidad de agua expulsada en la unidad de tiempo. Ahora bien, si el radio del orifico r de salida del agua es mucho más pequeño que el radio del depósito R, entonces g'≈g. La velocidad final vmáx depende solamente, de la masa M de la plataforma y depósito vacío, y de la masa inicial del agua en el depósito m0= ρπR2H.
A partir de este instante tmáx, el conjunto formado por la plataforma y depósito vacío se mueven con velocidad constante.
Ejemplo
-
El radio del depósito R=10 cm=0.1 m
-
El radio del orificio r=1 cm=0.01 m
-
El peso en vacío (sin agua) M=20 kg
-
La altura inicial del agua en el depósito H=45 cm=0.45 m
La masa inicial de agua en el depósito es
m0=ρπR2H, m0=1000·π·0.12·0.45=14.14 kg
Calculamos la aceleración de la gravedad efectiva g'
La velocidad inicial de salida del agua medida por un observador situado en la plataforma es
El tiempo que tarda en salir el agua del depósito es
La velocidad máxima que adquiere la plataforma es
La plataforma se encuentra en la posición
R=0.1; %radio del depósito
r=0.01; %radio del orificio
M=20; %peso en vacío
H=0.45; %altura inicial de agua en el depósito
m0=1000*pi*0.1^2*0.45; %masa inicial de agua
g=9.8/(1-(r/R)^4); %aceleración de la gravedad efectiva
%tiempo que tarda en salir el agua del depósito
tf=sqrt(((R/r)^4-1)*2*H/9.8);
vMax=2*sqrt(2*g*H)*(1-sqrt(M/m0)*atan(sqrt(m0/M)));
xMax=2*(R/r)^2*H*(1-(M/m0)*log(1+m0/M));
fprintf('Tiempo %2.1f, Velocidad final %4.1f, posición final %5.1f\n',
tf, vMax,xMax);
%representación gráfica
k=r^2*sqrt(pi*1000*g/2)/R;
%t=0:0.05:tf;
subplot(2,1,1);
v=@(t) (2/R)*sqrt(2*g/(pi*1000))*(k*t+sqrt(M)*atan((sqrt(m0)-k*t)
/sqrt(M))-sqrt(M)*atan(sqrt(m0/M)));
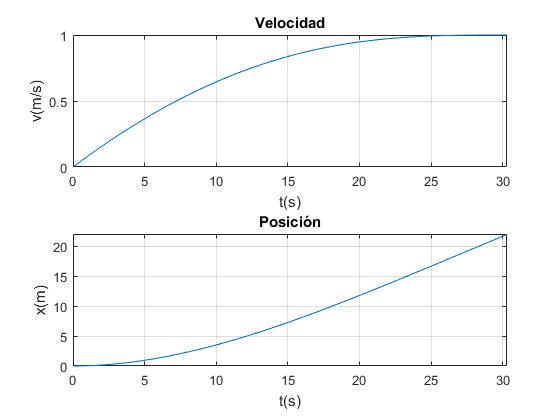
fplot(v,[0,tf])
grid on
xlabel('t(s)')
ylabel('v(m/s)')
title('Velocidad')
subplot(2,1,2);
x=@(t) (2/R)*sqrt(2*g/(pi*1000))*(k*t.^2/2-sqrt(M)*atan(sqrt(m0/M))
*t-(M/k)*((sqrt(m0)-k*t).*atan((sqrt(m0)-k*t)/sqrt(M))/sqrt(M)-
log(1+(sqrt(m0)-k*t).^2/M)/2-sqrt(m0/M)*atan(sqrt(m0/M))+log(1+m0/M)/2));
fplot(x,[0,tf])
grid on
xlabel('t(s)')
ylabel('x(m)')
title('Posición')
Tiempo 30.3, Velocidad final 1.0, posición final 21.9
Actividades
Se introduce:
- El radio del depósito, en el control titulado Radio depósito
- El radio del orificio situado en la parte lateral izquierda, en el control titulado Radio orificio
- El peso en vacío del depósito y de la plataforma, en el control titulado Masa vacío.
Se pulsa en el botón titulado Nuevo
- La altura inicial de agua en el depósito, se ha fijado en 45 cm.
Una vez que se define el estado inicial. Se pulsa el botón titulado ►.
Observamos la salida del agua por la parte inferior izquierda del depósito. Una flecha de color azul nos indica la magnitud de la velocidad de salida del agua medida por un observador situado en la plataforma. Una flecha de color rojo, nos indica la velocidad de la plataforma. La diferencia entre los dos vectores es igual a la velocidad de salida del agua medida por un observador situado en Tierra.
La velocidad de salida del agua medida por el observador situado en Tierra, primero es negativa, cuando el depósito comienza a vaciarse y luego es positiva, cuando el depósito está casi vacío. En un instante dado, la velocidad de salida del agua, coincide con la velocidad de la plataforma, la velocidad de salida del agua respecto del observador situado en Tierra es cero.
En la parte superior derecha, el programa interactivo nos proporciona los datos del tiempo (en s), la posición del depósito (su lado izquierdo, donde se encuentra el orificio), y la velocidad de la plataforma. Cuando, el agua ha salido del depósito, la plataforma se mueve con velocidad constante.
Nota: El lector se habrá dado cuenta que el depósito está dibujado a una escala, y el camino horizontal que recorre está dibujado a una escala distinta. Esto no afecta a la simulación, pero permite ver con claridad el proceso físico.
Referencias
Lapidus, R. Problem: Torricelli's rocket. Am. J. Phys. 54 (3) March 1986, (enunciado en la pág. 238, solución en la pág. 277)

