Principio de conservación de la energía

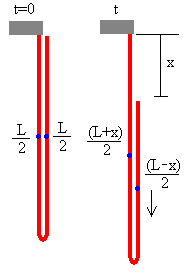
En la situación inicial t=0, la cadena está doblada en dos partes iguales de longitud L/2. Los centros de masa de cada una de las dos porciones, señalados por un punto de color azul, se encuentran a una distancia L/4 del por debajo de los extremos. Tomando como nivel cero de energía potencial la posición de ambos extremos en el instante t=0. La energía de la cadena en este instante es

${\displaystyle E=-\rho \frac{L}{2}g\frac{L}{4}-\rho \frac{L}{2}g\frac{L}{4}=-\rho g\frac{L^2}{4}}$

En el instante t, el extremo libre ha descendido una altura x. La cadena se encuentra doblada, pero la longitud de cada una de las porciones es distinta. La porción izquierda, tiene una longitud (L+x)/2 y la porción derecha (L-x)/2. La porción izquierda de la cadena se encuentra en reposo. La porción derecha se mueve con velocidad dx/dt. La energía de la cadena en el instante t es

${\displaystyle \begin{array}{l}E=\frac{1}{2}\rho \frac{L-x}{2}{\left(\frac{dx}{dt}\right)}^2-\rho \frac{L+x}{2}g\frac{L+x}{4}-\rho \frac{L-x}{2}g\frac{L-x}{4}=\\ \frac{1}{4}\rho (L-x){\left(\frac{dx}{dt}\right)}^2-\frac{\rho g}{4}\left(L^2+2Lx-x^2\right)\end{array}}$

Como la energía se conserva, despejamos la velocidad dx/dt.

${\displaystyle \frac{dx}{dt}=\sqrt{g\frac{x(2L-x)}{L-x}}}$

Integramos para determinar la posición x del extremo libre en función del tiempo t.

${\displaystyle \sqrt{g}{\displaystyle \underset{0}{\overset{t}{\int }}dt}={\displaystyle \underset{0}{\overset{x}{\int }}\sqrt{\frac{x(2L-x)}{L-x}}}dx}$

Se hace el cambio de variable

${\displaystyle \begin{array}{l}x=L{\sin }^2\phi \\ \sqrt{g}t=2\sqrt{L}{\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{{\cos }^2\phi }{\sqrt{1+{\cos }^2\phi }}d\phi }\frac{\sqrt{g}}{2\sqrt{L}}t={\displaystyle \underset{0}{\overset{\theta }{\int }}\sqrt{1+{\cos }^2\phi }}d\phi -{\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{d\phi }{\sqrt{1+{\cos }^2\phi }}}\\ \frac{\sqrt{g}}{2\sqrt{L}}t=\sqrt{2}{\displaystyle \underset{0}{\overset{\theta }{\int }}\sqrt{1-{\left(\frac{1}{\sqrt{2}}\right)}^2{\sin }^2\phi }}d\phi -\frac{1}{\sqrt{2}}{\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{d\phi }{\sqrt{1-{\left(\frac{1}{\sqrt{2}}\right)}^2{\sin }^2\phi }}}\end{array}}$

Las integrales elípticas de primera y segunda especie son

${\displaystyle F(\theta ,k)={\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{d\phi }{\sqrt{1-k^2{\sin }^2\phi }}}E(\theta ,k)={\displaystyle \underset{0}{\overset{\theta }{\int }}\sqrt{1-k^2{\sin }^2\phi }d\phi }}$

En términos de las integrales elípticas, la posición x del extremo libre es una función implícita del tiempo t.

${\displaystyle \begin{array}{l}\frac{\sqrt{g}}{\sqrt{2L}}t=2E\left(\theta ,\frac{1}{\sqrt{2}}\right)-F\left(\theta ,\frac{1}{\sqrt{2}}\right)\hfill \\ {\sin }^2\theta =\frac{x}{L}\hfill \end{array}}$

El tiempo total t que emplea el extremo libre la cadena en caer completamente, x=L, θ=π/2 se calcula resolviendo las integrales elípticas completas de primera y segunda especie.

${\displaystyle \sqrt{\frac{g}{2L}}t=2E\left(\frac{\pi }{2},\frac{1}{\sqrt{2}}\right)-F\left(\frac{\pi }{2},\frac{1}{\sqrt{2}}\right)}$

El valor del segundo miembro es 0.8472.

>> [K,E]=ellipke(1/2);
>> z=2*E-K
z =    0.8472

Alternativamente

> 2*ellipticE(pi/2,1/2)-ellipticF(pi/2,1/2)
ans =    0.8472

El tiempo t que tarda en caer la cadena es menor que el tiempo $t_0=\sqrt{2L/g}$ que tarda una partícula en caer libremente una altura L

t =0.8472·t₀

El tiempo que tarda en caer una cadena doblada de L=1m de longitud es t=0.383 s.

Como vemos, la aceleración de caída de la parte derecha de la cadena es mayor que la aceleración de la gravedad.

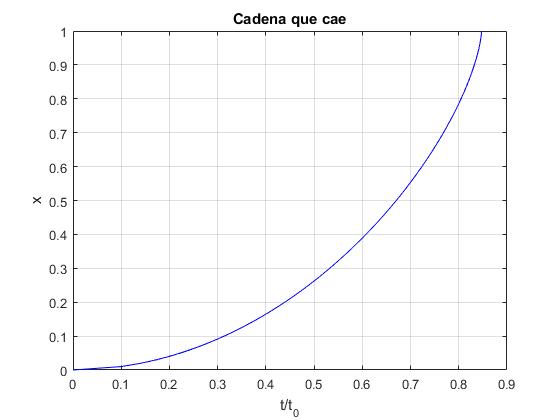
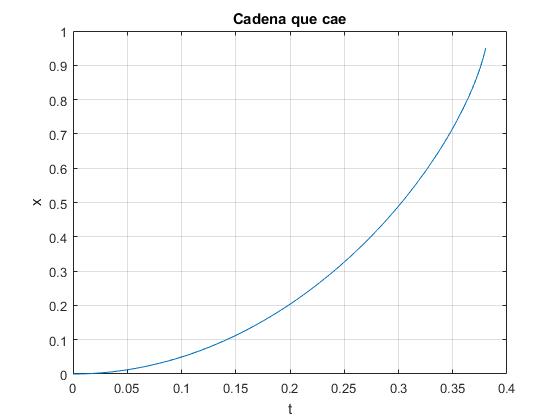
El siguiente código, calcula el instante t/t₀ cuando se proporciona la posición del extremo libre x/L de la cadena. Es decir, calcula la diferencia entre las dos integrales elípticas

${\displaystyle \begin{array}{l}\frac{t}{t_0}=2E\left(\theta ,\frac{1}{\sqrt{2}}\right)-F\left(\theta ,\frac{1}{\sqrt{2}}\right)\hfill \\ {\sin }^2\theta =\frac{x}{L}\hfill \end{array}}$

x=linspace(0,1,100);
t=2*ellipticE(asin(sqrt(x)),1/2)-ellipticF(asin(sqrt(x)),1/2);
plot(t,x,'b')
ylabel('x')
xlabel('t/t_0')
title('Cadena que cae')
grid on

Ecuaciones del movimiento

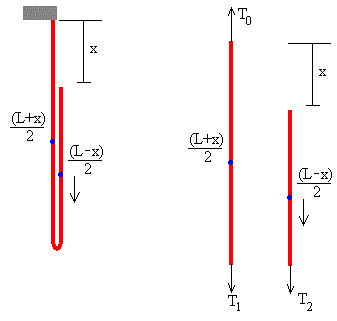
Las fuerzas sobre la porción derecha de la cadena son el peso y la fuerza T₂. La fuerza T₂ se debe sumar al peso para que la aceleración de esta parte de la cadena sea mayor que g. La ecuación del movimiento es

${\displaystyle \rho \frac{L-x}{2}\frac{d^{2}x}{d{t}^2}=\rho \frac{L-x}{2}g+T_2}$

Las fuerzas sobre la porción de la cadena en reposo son:

• T₀ la fuerza que ejerce el soporte fijo
• La fuerza T₁ en su parte inferior
• Su peso

${\displaystyle T_0=\rho \frac{L+x}{2}g+T_1}$

T₁ y T₂ deben ser iguales ya que la parte inferior de la porción derecha de la cadena y la parte inferior de la porción izquierda de la cadena están muy próximas. La tensión en la cadena debe ser continua.

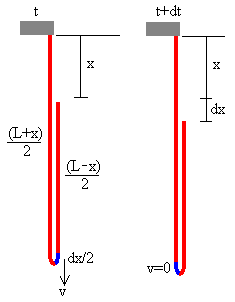
Cuando el extremo libre de la cadena se desplaza dx, una porción dx/2 de la cadena pasa del lado derecho al lado izquierdo, su velocidad se modifica de v=dx/dt a 0, su momento lineal cambia dp=ρ(dx/2)v. Para poner en reposo este elemento de masa en un tiempo dt se precisa de una fuerza en la unión de las dos porciones de cadena.

${\displaystyle T_1+T_2=\frac{dp}{dt}=\frac{\rho }{2}\frac{dx}{dt}v=\frac{1}{2}\rho {\left(\frac{dx}{dt}\right)}^2}$

La ecuación diferencial del movimiento del extremo libre de la cadena se escribe

${\displaystyle \begin{array}{l}\rho \frac{L-x}{2}\frac{d^{2}x}{d{t}^2}=\rho \frac{L-x}{2}g+\frac{1}{4}\rho {\left(\frac{dx}{dt}\right)}^2\\ \frac{d^{2}x}{d{t}^2}=g+\frac{1}{2(L-x)}{\left(\frac{dx}{dt}\right)}^2\end{array}}$

Tomando la longitud de la cadena L=1. Se resuelve la ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, la posición del extremo libre de la cadena es x=0, y parte del reposo, dx/dt=0.

f=@(t,x) [x(2);9.8+x(2)^2/(2*(1-x(1)))]; 
[t,x]=ode45(f,[0,10],[0,0]);
plot(t,x(:,1))
xlabel('t')
ylabel('x');
title('Cadena que cae')
grid on

El proceso de integración se detiene y produce un aviso (Warning) cuando la variable x, en el código x(1), toma el valor 1. Para evitar este aviso integramos la ecuación diferencial hasta x=0.95 Para ello, definimos la función detiene_ode45

function [value,isterminal,direction]=detiene_ode45(~,x)
    value=x(1)-0.95; 
    isterminal=1;
    direction=0; 
end

Se pasa esta función al procedimiento ode45

f=@(t,x) [x(2);9.8+x(2)^2/(2*(1-x(1)))]; 
opts=odeset('events',@detiene_ode45);
[t,x]=ode45(f,[0,0.4],[0,0], opts);
plot(t,x(:,1))
xlabel('t')
ylabel('x');
title('Cadena que cae')
grid on

Fuerza que ejerce el soporte

La fuerza que ejerce el soporte sobre el extremo fijo de la cadena vale

${\displaystyle T_0=\rho \frac{L+x}{2}g+\frac{1}{4}\rho {\left(\frac{dx}{dt}\right)}^2}$

Aplicando el principio de conservación de la energía, obtuvimos la velocidad dx/dt de caída

${\displaystyle T_0=\rho g\left(\frac{L+x}{2}+\frac{1}{4}\frac{x(2L-x)}{L-x}\right)}$

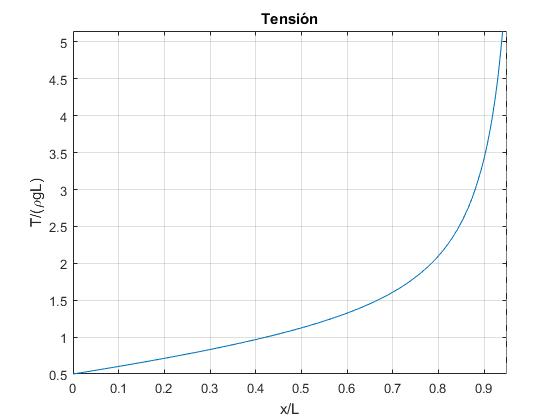
En la figura, se representa T₀/(ρgL) en función de x/L. Cuando x→L, T₀→∞,

f=@(x) (1+x)/2+(x.*(2-x))./(4*(1-x));
fplot(f,[0,0.95])
xlabel('x/L')
ylabel('T/(\rhogL)')
title('Tensión')
grid on

Actividades

• La cadena tiene una longitud de L=1.0 y su densidad lineal se ha fijado en ρ=1.0 kg/m.

Se pulsa el botón titulado Nuevo

Se observa la caída de la cadena. Se proporciona los datos del tiempo t, la posición x de su extremo libre y la velocidad v=dx/dt.

En un diagrama en forma de tarta, comprobamos que se cumple el principio de conservación de la energía, la energía potencial se transforma integramente en energía cinética. La energía potencial se representa en color azul, y la energía cinética en color rojo.

La gráfica, muestra la fuerza T₀ que ejerce el soporte sobre la cadena en función del tiempo t.

Referencias

Calkin M. G., March R. H. The dynamics of a falling chain: I. Am. J. Phys. 57 (2) February 1989, pp. 154-157