Oscilaciones

Sea un recipiente cilíndrico de masa M y radio R. Se coloca sobre la superficie del agua y se suelta. Cuando se ha sumergido x, las fuerzas que actúan sobre el recipiente son

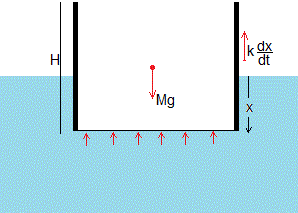
• El peso, Mg
• La fuerza que ejerce la presión en el fondo del recipiente,(ρgx)S=(ρgx)πR²

La ecuación del movimiento es

${\displaystyle \begin{array}{l}M\frac{d^{2}x}{d{t}^2}=Mg-\left(\rho gx\right)S\\ \frac{d^{2}x}{d{t}^2}+\frac{\rho gS}{M}x=g\end{array}}$

La solución particular de esta ecuación diferencial es una constante C, introduciendo en la ecuación diferencial

${\displaystyle \frac{\rho gS}{M}C=g,C=\frac{M}{\rho S}}$

La solución de la ecuación diferencial homogénea es de la forma

${\displaystyle x_h=A\cos ({\omega }_{0}t)+B\sin ({\omega }_{0}t),{\omega }_0^2=\frac{\rho gS}{M}}$

La solución completa es la suma de la particular y de la homogénea

${\displaystyle \begin{array}{l}x=A\cos ({\omega }_{0}t)+B\sin ({\omega }_{0}t)+\frac{M}{\rho S}\\ \frac{dx}{dt}={\omega }_0\left(-A\sin ({\omega }_{0}t)+B\cos ({\omega }_{0}t)\right)\end{array}}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales , t=0, x=0, dx/dt=0

${\displaystyle \begin{array}{l}B=\mathrm{0,}A=-\frac{M}{\rho S}\\ x=\frac{M}{\rho S}\left(1-\cos ({\omega }_{0}t)\right)=2\frac{M}{\rho S}{\sin }^2\left(\frac{{\omega }_0}{2}t\right)\end{array}}$

Oscilaciones amortiguadas

Ahora bien, debido a la viscosidad de agua, la amplitud de las oscilaciones no es constante sino que disminuye con el tiempo, debido a una fuerza de rozamiento proporcional a la velocidad. La ecuación del movimiento es

${\displaystyle \begin{array}{l}M\frac{d^{2}x}{d{t}^2}=Mg-\left(\rho gx\right)S-k\frac{dx}{dt}\\ \frac{d^{2}x}{d{t}^2}+\frac{k}{M}\frac{dx}{dt}+\frac{\rho gS}{M}x=g\end{array}}$

La solución particular es la misma y la solución completa tiene la forma

${\displaystyle \begin{array}{l}x=\exp \left(-\gamma t\right)\left(A\sin \left(\omega t\right)+B\cos \left(\omega t\right)\right)+\frac{M}{\rho S},\{\begin{array}{l}2\gamma =\frac{k}{M}\\ {\omega }^2={\omega }_0^2-{\gamma }^2\end{array}\\ \frac{dx}{dt}=-\gamma \exp \left(-\gamma t\right)\left(A\sin \left(\omega t\right)+B\cos \left(\omega t\right)\right)+\exp \left(-\gamma t\right)\omega \left(A\cos \left(\omega t\right)-B\sin \left(\omega t\right)\right)\end{array}}$

Con las condiciones iniciales especificadas, t=0, x=0, dx/dt=0

${\displaystyle x=\frac{M}{\rho S}\left(1-\exp \left(-\gamma t\right)\left(\frac{\gamma }{\omega }\sin \left(\omega t\right)+\cos \left(\omega t\right)\right)\right)}$

• Masa del recipiente, M=101.69 g
• Fondo del recipiente de radio, R=41.71 mm
• Densidad del agua ρ=1000 kg/m³
• Constante k=0.19, (rozamiento viscoso)

Representamos la posición x (m) del recipiente en función del tiempo t (s)

M=101.69/1000; %masa del recipiente
rho=1000; %densidad del agua
S=pi*(41.71/1000)^2; %fondo del recipiente
k=0.19; %rozamiento viscoso
g=k/(2*M); %constante de amortiguamiento
w0=sqrt(rho*9.8*S/M); %frecuencia natural
w=sqrt(w0^2-g^2);
f=@(t) M*(1-exp(-g*t).*(g*sin(w*t)/w+cos(w*t)))/(rho*S);
fplot(f,[0,6])
disp(M/(rho*S)) %posición final
grid on
ylim([0,0.04])
xlabel('t')
ylabel('x');
title('Oscilación amortiguada')

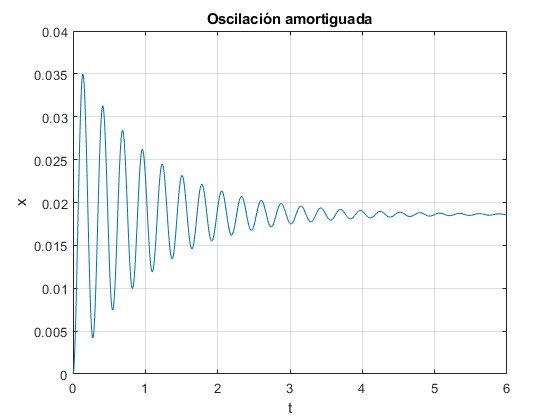
La posición final t→∞ es la de equilibrio entre el peso y el empuje

${\displaystyle \begin{array}{l}Mg=\rho gS{x}_{\infty }\\ x_{\infty }=\frac{M}{\rho S}\end{array}}$

   0.01861

Sistema de masa variable

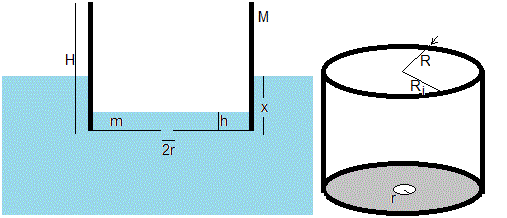
Sea un recipiente de forma cilíndrica abierto por arriba de masa M y altura H. Las paredes del recipiente tienen un espesor no nulo de modo que su radio interior es R_i y su radio exterior es R, en el fondo hay un pequeño agujero de radio r. Se coloca sobre la superficie del agua, que entra por el agujero con velocidad v

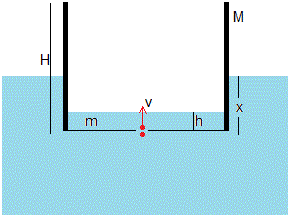
Aplicamos la ecuación de Bernoulli a dos puntos situados por debajo y por encima del agujero. El agua está en casi en reposo por debajo del recipiente y sale del agujero con velocidad v

${\displaystyle \begin{array}{l}\rho gx+p_a=\frac{1}{2}\rho v^2+\rho gh+p_a\\ v=\sqrt{2g\left(x-h\right)}\end{array}}$

donde p_a es la presión atmosférica.

La velocidad real es algo más pequeña

${\displaystyle v=c\sqrt{2g\left(x-h\right)}}$

donde c≈0.7 es un factor de corrección

Masa del recipiente que contiene agua

El recipiente contiene agua hasta una altura h, su masa es m=ρhS_i. Donde ρ es la densidad del agua, S_i=πR_i² es la sección de recipiente.

La masa m del agua contenida en el recipiente se incrementa con el tiempo t, a razón

${\displaystyle \frac{dm}{dt}=\rho S_{h}v=\rho S_{h}c\sqrt{2g\left(x-h\right)}}$

S_h=πr² es la sección del agujero

Ecuación del movimiento

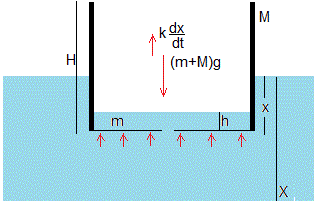
Las fuerzas sobre el recipiente de masa M+m que contiene agua son

• El peso, (M+m)g
• La fuerza que ejerce la presión en el fondo del recipiente,(ρgx)S=(ρgx)πR²
• La fuerza de rozamiento, proporcional a la velocidad dx/dt y de signo contrario a ésta (debido a la viscosidad de agua)

La ecuación del movimiento de este sistema de masa variable es

${\displaystyle \frac{dp}{dt}=\left(m+M\right)g-\rho gxS-k\frac{dx}{dt}}$

Donde p es el momento lineal del sistema

${\displaystyle p=(M+m)\frac{dx}{dt}}$

Obtenemos la ecuación diferencial

${\displaystyle \begin{array}{l}(M+m)\frac{d^{2}x}{d{t}^2}+\frac{dm}{dt}\frac{dx}{dt}=\left(m+M\right)g-\rho gxS-k\frac{dx}{dt}\\ \frac{d^{2}x}{d{t}^2}=g-\frac{\rho gS}{M+m}x-\frac{\rho S_{h}c\sqrt{2g\left(x-h\right)}+k}{M+m}\frac{dx}{dt}\end{array}}$

Teniendo en cuenta, que el agua contenida en el recipiente m=ρS_ih. Tenemos que resolver el sistema de dos ecuaciones diferenciales

${\displaystyle \{\begin{array}{l}\frac{dh}{dt}=\frac{S_h}{S_i}c\sqrt{2g\left(x-h\right)}\\ \frac{d^{2}x}{d{t}^2}=g-\frac{\rho gS}{M+\rho S_{i}h}x-\frac{\rho S_{h}c\sqrt{2g\left(x-h\right)}+k}{M+\rho S_{i}h}\frac{dx}{dt}\end{array}}$

con las condiciones iniciales, t=0, x=0, dx/dt=0, h=0

El proceso de integración se interrumpe cuando x≥H, cuando el recipiente se hunde completamente en el agua

Ejemplos

• Altura del recipiente, H=46 mm
• Masa del recipiente, M=101.69 g
• Fondo del recipiente de radio, R=41.71 mm
• Radio interior, R_i=37.33 mm
• Radio del agujero, r=2.00 mm
• Densidad del agua ρ=1000 kg/m³
• Constante k=0.19, (rozamiento viscoso)
• Coeficiente de corrección, c=0.7

Representamos la posición x (m) del recipiente en función del tiempo t (s)

function cuenco
    H=46/1000; %altura del recipiente
    M=101.69/1000; %masa del recipiente
    rho=1000; %densidad del agua
    Sh=pi*(2/1000)^2; %sección del agujero
    S=pi*(41.71/1000)^2; %fondo del recipiente
    Si=pi*(37.33/1000)^2; %sección interior
    k=0.19; %rozamiento viscoso
    c=0.7; %coeficiente de corrección
    %x(2) es dx/dt, x(1) es x, x(3) es h
    opts=odeset('events',@stop_bowl);
    f=@(t,x) [x(2); 9.8-(k+rho*Sh*c*sqrt(2*9.8*(x(1)-x(3))))*x(2)/
(M+rho*x(3)*Si)-rho*9.8*S*x(1)/(M+rho*x(3)*Si); Sh*c*sqrt(2*9.8*(x(1)-x(3)))/Si];
    [t,x]=ode45(f,[0,200],[0,0,0],opts);
    disp(t(end))%cuando se hunde
    plot(t,x(:,1))
    grid on
    xlabel('t')
    ylabel('x');
    title('Se hunde un recipiente')

    function [value,isterminal,direction]=stop_bowl(~,x)
        value=x(1)-H;
        isterminal=1; %1 detiene la integración cuando x=H   
        direction=1; % 1 crece, -1 decrece, 0 no importa
    end
end

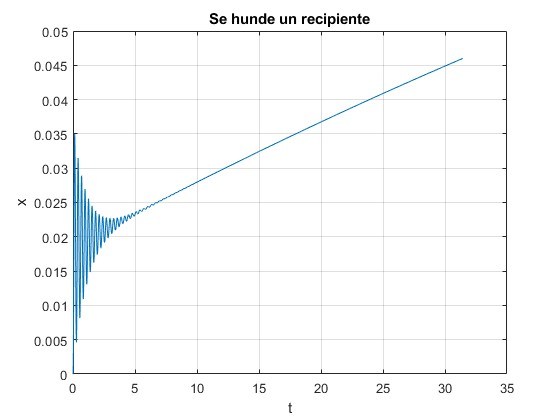
El recipiente queda completamente sumergido, en el instante

  31.4320

Observamos que al principio que el recipiente describe oscilaciones amortiguadas, cuya amplitud disminuye con el tiempo. Véase la animación más abajo

Cambiamos algunos de los valores de los parámetros

• Masa del recipiente, M=102.01 g
• Fondo del recipiente de radio, R=41.78 mm
• Radio interior, R_i=37.75 mm
• Radio del agujero, r=2.40 mm

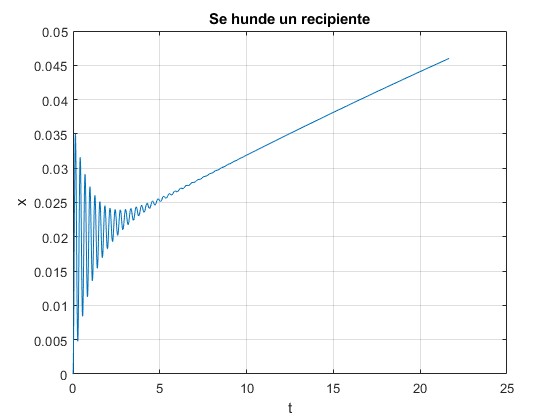
El recipiente queda completamente sumergido, en el instante

  21.6643

Cambiamos algunos de los valores de los parámetros

• Masa del recipiente, M=104.08 g
• Fondo del recipiente de radio, R=42.50 mm
• Radio interior, R_i=38.75 mm
• Radio del agujero, r=1.00 mm

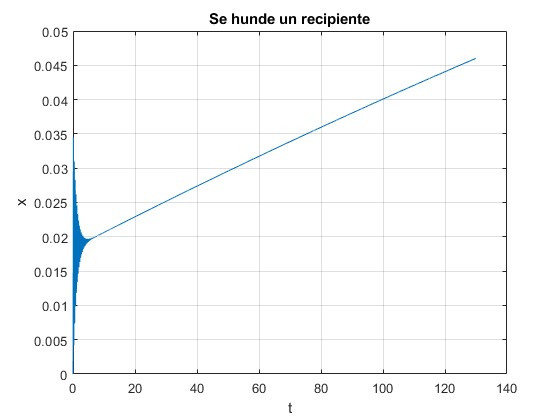
El recipiente queda completamente sumergido, en el instante

  129.9233

Actividades

Se introduce

• La masa M del recipiente en g, en el control titulado Masa
• El radio del fondo del recipiente R en mm, en el contro titulado Radio fondo
• El radio interior del recipiente R_i en mm, en el contro titulado Radio interior
• El radio del agujero en el fiondo del recipiente r en mm, en el contro titulado Radio agujero

Se pulsa el botón titulado Nuevo

Se observa, al principio, un movimiento oscilatorio cuya amplitud disminuye con el tiempo, el recipiente se va sumergiendo a medida que entra el agua a través del agujero situado en el centro del fondo hasta que se hunde completamente.

Cuando el recipiente está completamente sumergido, se detiene la animación y se anota el tiempo final t_s en s

La flecha de color rojo, indica la velocidad del agua que entra en el recipiente

En la parte superior izquierda, se proporcionan los datos del tiempo en s, posición del fondo del recipiente x y altura h de agua que contiene el recipiente, ambas en mm

Se sugiere al lector experimentar con el programa interactivo

• Mantiendo fijos, la masa M=100 g, el radio R=42 mm y el radio interior R_i=38 mm. Cambiar el radio del agujero a 1, 1.25, 1.5, 1.7 y 2 mm. Anotar el tiempo t_s para cada caso

• Mantiendo fijos, el radio R=42 mm y el radio interior R_i=38 mm y el radio del agujero r=1.7 mm. Cambiar la masa M a 80, 90, 100, 110, 120 g. Anotar el tiempo t_s para cada caso

Referencias

Wang Xing, Li Qiu-hang, Hou Ji-xuan, Chen Qian. Exploration of the sinking of Saxon bowl:correction of simple harmonic vibration. College Physics. Vol. 40, No. 11, November 2021