El flujo de arena

El flujo (masa por unidad de tiempo) de un material granular de densidad ρ a través de una abertura de área A bajo la acción del campo gravitatorio terrestre g, es

$\frac{d m}{d t} = k ρ \sqrt{g} A^{\frac{5}{4}}$

donde k es una constante.

Como se estudiará en el capítulo Fluidos, el flujo de un líquido a través de una abertura depende de la altura del líquido y por tanto, depende del tiempo.

Vamos a diseñar una “experiencia” con el objetivo de:

comprobar que el flujo de arena es constante en el tiempo y no depende de la altura h de la columna de arena.
determinar la dependencia del flujo con el área A del orificio de salida.

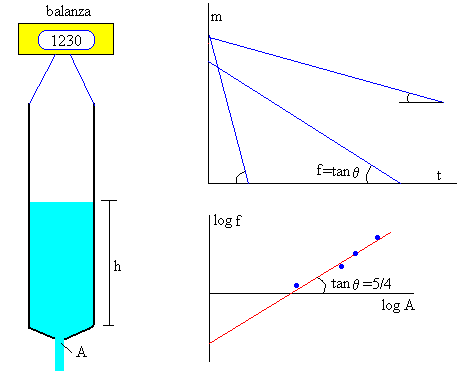
Dispondremos de una botella de plástico invertida, en la que podemos cambiar el radio del orificio de salida.

La botella se cuelga de una balanza o de un dispositivo de medición de fuerzas conectado a un sistema de adquisición de datos. De este modo, se mide la masa en función del tiempo.

Representando gráficamente, en el eje vertical la masa m de arena contenida en la botella y en el eje horizontal, el tiempo t. Obtenemos una línea recta cuya pendiente es -dm/dt. De este modo, comprobamos que el flujo es constante

Para determinar la dependencia del flujo f =dm/dt con el área A del orificio de salida, escribimos

$f = c \cdot A^{n} \log f = \log c + n \log A$

donde c es una constante. Cambiamos el radio del orificio y repetimos el experimento, midiendo una nueva pendiente -f y así, sucesivamente.

Si representamos logf en el eje vertical y logA en el eje horizontal, obtenemos una línea recta cuya pendiente n es próxima a 5/4 tal como se muestra en la parte inferior de la figura.

Actividades

Se Introduce

El diámetro d del orificio de salida en mm, en el control titulado Diámetro
La altura inicial en cm de la arena en la botella invertida, en el control titulado Altura

Se pulsa el botón titulado Nuevo

El sensor de fuerza o la balanza electrónica, situada en la parte superior mide solamente el peso de arena, se ha descontado el peso de las partes que no cambian (botella, abertura, etc.).

Se observa la salida de la arena a través del orificio, comprobamos que el flujo es constante e independiente de la altura inicial de la arena en el recipiente.

En la parte derecha, observamos la representación gráfica de la masa m de la arena en función del tiempo t. En la parte superior, en letras grandes se proporcionan los datos de la pendiente de la recta (cambiada de signo), el flujo, f y el área de la abertura circular A=π·d²/4, siendo d el diámetro en mm.

Fijamos la altura incial h₀=20 cm y vamos cambiando el diámetro del orificio y pulsamos el botón titulado Nuevo y así, sucesivamente

Apuntamos los pares de datos (flujo, área) para representar

en el eje horizontal log A (el área en mm²)
en el eje vertical log f (el flujo en g/s)

d	6	7	8	9	10	11	12	13	14	15
A	28.3	38.5	50.3	63.6	78.5	95.0	113.1	132.7	153.9	176.7
f	8.6	12.6	17.6	23.6	30.7	39.0	48.4	58.8	70.6	83.9

area=[28.3,38.5,50.3,63.6,78.5,95.0,113.1,132.7,153.9,176.7];
flujo=[8.6,12.6,17.6,23.6,30.7,39.0,48.4,58.8,70.6,83.9];
plot(log(area),log(flujo), 'o', 'markersize',3,'markeredgecolor',
'r','markerfacecolor','r')
grid on
xlabel('log(A)')
ylabel('log(f)')
title('Flujo de arena')

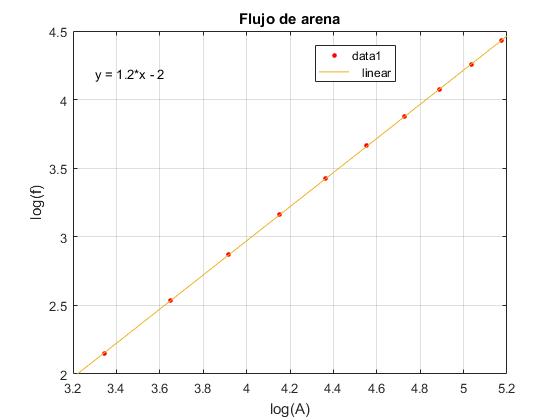
En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p1 y p2 del polinomio (recta) y=p1*x+p2 de ajuste.

El valor de la pendiente de la recta, p₁=1.2443, por lo que el exponente n del área es un valor próximo a 5/4=1.25

Diámetro (mm):
Altura (cm) h₀:

Una máquina de Atwood con un cuerpo de masa variable

Movimiento del cuerpo de masa variable

La segunda ley de Newton para el movimiento en una dimensión se escribe

$F = \frac{d p}{d t}$

donde p es el momento total del sistema y F la fuerza neta que actúa sobre el mismo. Como la masa del sistema varía con el tiempo, hemos de ser muy cuidadosos cuando nos referimos al momento p, ya que incluye el momento de la masa expulsada, tal como vimos en la formulación de las ecuaciones del movimiento de un cohete, que volvemos a reproducir en esta página.

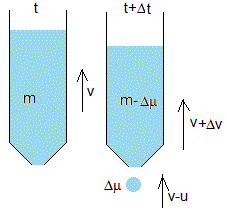
En el instante t el depósito de masa m lleva una velocidad v. Su momento lineal es

p(t)=mv

En el instante t+Δt

El depósito tiene una masa m-Δμ, su velocidad es v+Δv.
La masa de arena descargada Δμ lleva una velocidad –u respecto del depósito o una velocidad –u+ v, respecto de Tierra

El momento lineal del sistema en este instante es

p(t+Δt)=(m-Δμ)(v+Δv)+ Δμ(–u+ v)

La variación del momento lineal entre el instante t y el instante t+Δt es

Δp= p(t+Δt)- p(t)=m·Δv- u·Δμ-Δv·Δμ

En el límite cuando Δt→0

$\frac{d p}{d t} = m \frac{d v}{d t} - u \frac{d μ}{d t}$

La masa M del sistema formado por el depósito m y la arena descargada μ es constante M=μ+m, por lo que dμ+dm=0. La masa del depósito disminuye en dm y aumenta la masa de la arena descargada en la misma cantidad.

$\frac{d p}{d t} = m \frac{d v}{d t} + u \frac{d m}{d t}$

Si la velocidad u de salida de la arena respecto del depósito es cero, la ecuación del movimiento se escribe

$m \frac{d v}{d t} = F$

que es similar a la expresión para el caso de una masa constante, pero con la importante diferencia de que la masa es variable con el tiempo.

Máquina de Atwood

Colocamos el depósito de arena en una máquina de Atwood, tal como se muestra en la figura

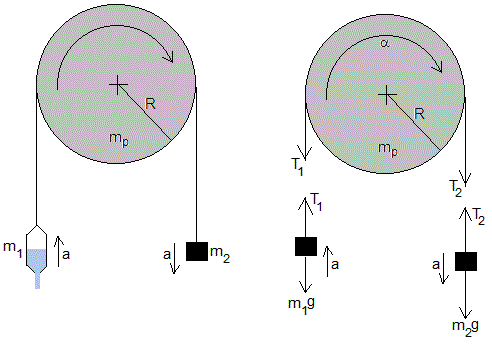
Esta máquina de Atwood está formada por

Un depósito de masa variable m₁ que disminuye a medida que cae la arena. Su ecuación del movimiento es

m₁a=T₁-m₁g

Un contrapeso de masa m₂. La ecuación del movimiento es

m₂a=m₂g-T₂

Una polea en forma de disco de masa m_p y momento de inercia m_pR²/2. La ecuación del movimiento es

(m_pR²/2)α=T₂R-T₁R

Eliminando T₁ y T₂ y relacionando la aceleración de los cuerpos a con la aceleración angular α del disco, a=αR

$a = \frac{m_{2} - m_{1}}{m_{2} + m_{1} + \frac{1}{2} m_{p}} g$

La masa del depósito es una función del tiempo

Cuando el depósito de arena se mueve verticalmente con una aceleración a, el flujo de arena se verá afectado, ya que cuando el depósito cae libremente, no habrá flujo de arena

El flujo f₀ de arena para un depósito en reposo es proporcional a la raíz cuadrada de la aceleración de la gravedad, g. El flujo para un depósito que se mueve con aceleración a será

$\frac{d m_{1}}{d t} = - f_{0} \sqrt{1 + \frac{a}{g}}$

De modo que, cuando a=-g (caída libre) el flujo es nulo

$\frac{d m_{1}}{d t} = - f_{0} \sqrt{\frac{2 m_{2} + \frac{1}{2} m_{p}}{m_{2} + \frac{1}{2} m_{p} + m_{1}}}$

En el instante t=0, la masa inicial del depósito de arena es m₁₀. En el instante t, la masa de dicho depósito es m₁

$\begin{array}{l} \int_{m_{10}}^{m_{1}} \sqrt{m_{2} + \frac{1}{2} m_{p} + m_{1}} \cdot d m_{1} = - \int_{0}^{t} f_{0} \sqrt{2 m_{2} + \frac{1}{2} m_{p}} \cdot d t \\ {(m_{2} + \frac{1}{2} m_{p} + m_{1})}^{3 / 2} = {(m_{2} + \frac{1}{2} m_{p} + m_{10})}^{3 / 2} - \frac{3}{2} f_{0} \sqrt{2 m_{2} + \frac{1}{2} m_{p}} \cdot t \\ m_{1} (t) = {{(m_{2} + \frac{1}{2} m_{p} + m_{10})}^{3 / 2} - \frac{3}{2} f_{0} \sqrt{2 m_{2} + \frac{1}{2} m_{p}} \cdot t}^{2 / 3} - m_{2} - \frac{1}{2} m_{p} \end{array}$

Suponiendo que la masa del recipiente es pequeña, el tiempo que tarda en vaciarse m₁=0, es

$t = \frac{2}{3} \frac{{(m_{2} + \frac{1}{2} m_{p} + m_{10})}^{3 / 2} - {(m_{2} + \frac{1}{2} m_{p})}^{3 / 2}}{f_{0} \sqrt{2 m_{2} + \frac{1}{2} m_{p}}}$

Aunque la masa del recipiente no sea despreciable, siempre se puede restar la masa del contrapeso de la masa del recipiente. De modo que, m₂ sería la diferencia entre la masa del contrapeso y la masa del recipiente vacío

Supongamos una máquina de Atwood compuesta por

Un depósito de arena de masa inicial, m₁₀=58.9 g
El flujo de arena cuando el depósito está en resposo es f₀=1.7 g/s
Un contrapeso, m₂=55.25 g
Una polea de masa, m_p=11 g

f0=1.7;  %flujo en reposo
m10=58.9; %masa incial de arena
m2=55.25; %contrapeso
mp=11; %polea

m1=@(t) ((m2+mp/2+m10)^(3/2)-3*f0*sqrt(2*m2+mp/2)*t/2).^(2/3)-m2-mp/2;
tf=2*((m2+mp/2+m10)^(3/2)-(m2+mp/2)^(3/2))/(3*f0*sqrt(2*m2+mp/2));
fplot(m1,[0,tf])
grid on
xlabel('t')
ylabel('m_1(t)');
title('masa de arena')

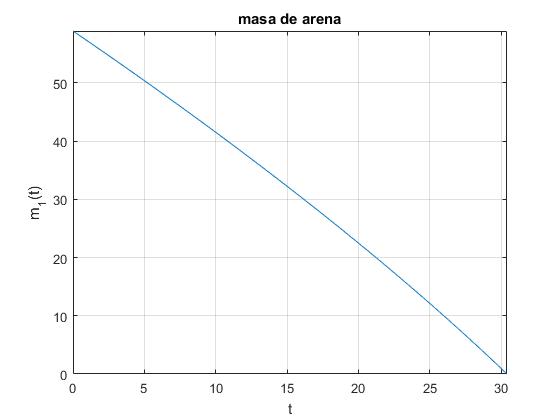
El tiempo que tarda en vaciarse el depósito de arena es

>> tf
tf =   30.4135

La ecuación del movimiento

Conocida la masa m₁ en función del tiempo t, la ecuación diferencial del movimiento de los cuerpos se escribe

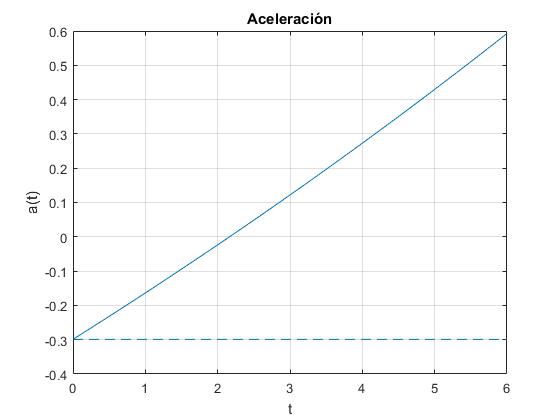
$\frac{d^{2} x}{d t^{2}} = \frac{m_{2} - m_{1} (t)}{m_{2} + \frac{1}{2} m_{p} + m_{1} (t)} g$

Se compara la aceleración de la máquina de Atwood de masa variable, con otra cuyas masas no cambian

f0=1.7;  %flujo en reposo
m10=58.9; %masa incial de arena
m2=55.25; %contrapeso
mp=11; %polea

m1=@(t) ((m2+mp/2+m10)^(3/2)-3*f0*sqrt(2*m2+mp/2)*t/2).^(2/3)-m2-mp/2;
acel=@(t) (m2-m1(t))*9.8./(m2+mp/2+m1(t));
fplot(acel,[0,6])
a=(m2-m10)*9.8/(m2+mp/2+m10); %masas fijas
line([0,6], [a,a],'lineStyle','--')
ylim([-0.4,0.6])
grid on
xlabel('t')
ylabel('a(t)');
title('Aceleración')

Se resuelve esta ecuación diferencial por procedimientos numéricos, con las siguientes condiciones inciales: en el instante t=0, la posición de partida x=0, en reposo, dx/dt=0

Primero, definimos la función a integrar

function fg = atwood_variable2(t,x, m10, m2,mp)
    m1=@(t) ((m2+mp/2+m10)^(3/2)-3*f0*sqrt(2*m2+mp/2)*t/2).^(2/3)-m2-mp/2;
    fg=[x(2);(m2-m1(t))*9.8/(m1(t)+m2+mp/2)];
end

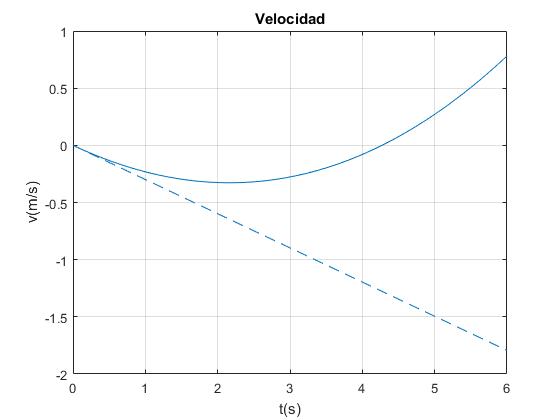
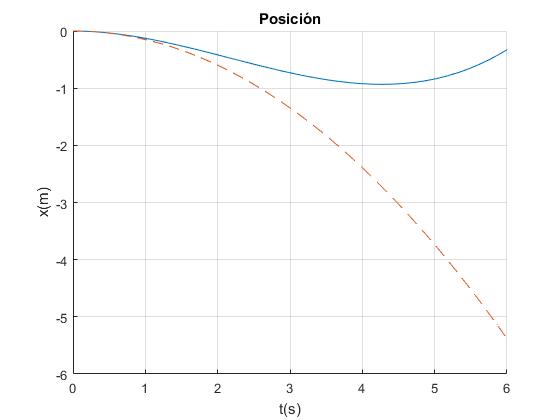
Creamos un script para llamar al procedimiento ode45 y pasarle la función a integrar. Representamos la velocidad dx/dt en función del tiempo y la posición x en función del tiempo t. Integramos la ecuación diferencial hasta el instante tf=6 s, que es menor que el tiempo que tarda en vaciarse el depósito de arena 30.4 s. Comparamos con la velocidad at y la posición at²/2 de la máquina de Atwood formada por cuerpos cuyas masas no cambian (líneas a trazos).

f0=1.7;  %flujo en reposo
m10=58.9; %masa incial de arena
m2=55.25; %contrapeso
mp=11; %polea
a=(m2-m10)*9.8/(m2+mp/2+m10); %aceleración, masas fijas

fg=@(t,x) atwood_variable2(t,x, f0, m10,m2,mp); 
tf=6; %tiempo final
[t,x]=ode45(fg,[0,tf],[0,0]);

figure
plot(t,x(:,2))
line([0,6],[0,a*tf],'lineStyle','--')
grid on
xlabel('t(s)')
ylabel('v(m/s)')
title('Velocidad')

figure
hold on
plot(t,x(:,1))
x=@(t) a*t.^2/2;
fplot(x,[0,tf], 'lineStyle','--')
hold off
grid on
xlabel('t(s)')
ylabel('x(m)');
title('Posición')

Referencias

Flores J., Solovey G., Gil S., Flow of sand and a variable mass Atwood machine. Am. J. Phys. 71 (7) July 2003, pp. 715-720.