Osciladores magnéticamente acoplados
Extendemos los resultados para un oscilador a dos osciladores acoplados iguales
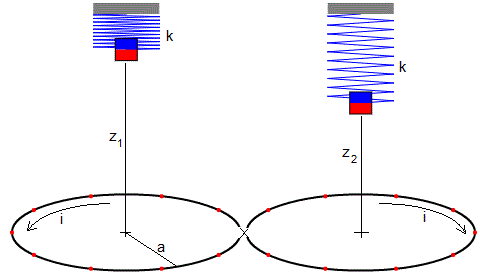
Cada oscilador consta de un muelle de constante k suspendido verticalmente. Se cuelga de su extremo libre inferior un potente imán de momento magnético μ. A una distancia z10 y z20 por debajo del imán se coloca una bobina formada por un conjunto de N espiras apretadas del mismo radio a.
Al moverse los imanes, el campo magnético variable induce una corriente en las espiras de la bobina. Dicha corriente establece una fuerza sobre el imán que se opone a su velocidad.
El acoplamiento consiste en unir las dos bobinas, de modo que son recorridas por la misma corriente
La figura muestra la disposición de los osciladores en un instante t, el primer imán dista del centro de la bobina z1 y el segundo, z2
Supondremos que los osciladores estarán suficientemente alejados entre sí, de modo que el campo magnético producido por el primer imán no afecte a la bobina del segundo imán y viceversa
La corriente inducida en las bobinas
El moverse los imanes inducen en las bobinas situadas debajo las fem V1 y V2 que ya hemos calculado
Donde N es el número de espiras del mismo radio a
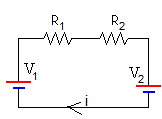
La intensidad de la corriente que circula por las dos bobinas conectadas es
Donde R1 y R2 son las resistencias de las bobinas, que son iguales. Se puede añadir la resistencia de los cables de conexión
D es el diámetro de la sección del cable y σ la conductividad del material del que está hecho el cable
La expresión de la intensidad i es
La fuerza que ejercen las corrientes inducidas en las bobinas sobre cada uno de los imanes son:
Ecuaciones del movimiento
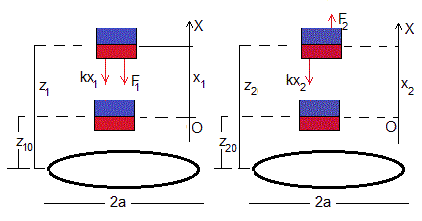
La fuerza que se opone al movimiento del primer imán es proporcional a su velocidad dx1/dt y de sentido contrario.
Sea z10 la altura inicial del imán en equilibrio sobre la bobina. Cuando el imán se desplaza x1=z1-z10 de la posición de equilibrio las fuerzas que actúan sobre el imán son:
- La fuerza que ejerce el muelle deformado kx1, siendo k es la constante del muelle
- La fuerza F1 que ejerce la corriente inducida en la bobina sobre el imán, que es una función de z1 o de x1=z1-z10
La misma argumentación se repite para el segundo imán.
Las ecuaciones del movimiento de los imanes son
Tenemos un sistema de dos ecuaciones diferenciales que se resuelven por procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, x1=x10, (dx1/dt)=0, x2=x20, (dx2/dt)=0.
N=10; %número de espiras
mu=2.6; %momento magnético del imán
sigma=2.741e7; %conductividad del cable
D=0.15; %cm, sección del cable
a=1.5; %radio de la espira en cm
m=0.055; %masa del imán
k=3.17; %constante elástica
z10=1.7; %separación inicial entre el imán y la espira
z20=1.7; %separación inicial entre el imán y la espira
cte=N*1e6*9*(4*pi*1e-7)^2*2.6^2*2.741e7*D^2*a^3/(64*m);
w0=sqrt(k/m);
tspan=[0,5];
x0=[0.5,0,-0.5,0]; %condiciones iniciales
% x1=x(1), dx1/dt=x(2), x2=x(3), dx2/dt=x(4)
fg=@(t,x)[x(2);-cte*((z10+x(1))^2*x(2)/(a^2+(z10+x(1))^2)^5
-(z10+x(1))*(z20+x(3))*x(4)/((a^2+(z10+x(1))^2)^(5/2)*
(a^2+(z20+x(3))^2)^(5/2)))-w0^2*x(1);...
x(4); -cte*(-(z10+x(1))*(z20+x(3))*x(2)/((a^2+(z10+x(1))^2)^(5/2)*
(a^2+(z20+x(3))^2)^(5/2))+(z20+x(3))^2*x(4)/(a^2+(z20+x(3))^2)^5)
-w0^2*x(3)];
[t,x]=ode45(fg,tspan,x0);
plot(t,x(:,1),t,x(:,3))
xlabel('t')
ylabel('x_1,x_2')
title('Posiciones')
grid on
cte=3*(4*pi*1e-7)*2.6*2.741e7*D^2*a/32;
inten=cte*((z10+x(:,1)).*x(:,2)./(a^2+(z10+x(:,1)).^2).^(5/2)
-(z20+x(:,3)).*x(:,4)./(a^2+(z20+x(:,3)).^2).^(5/2));
figure
plot(t,inten)
xlabel('t')
ylabel('i')
title('Intensidad')
grid on
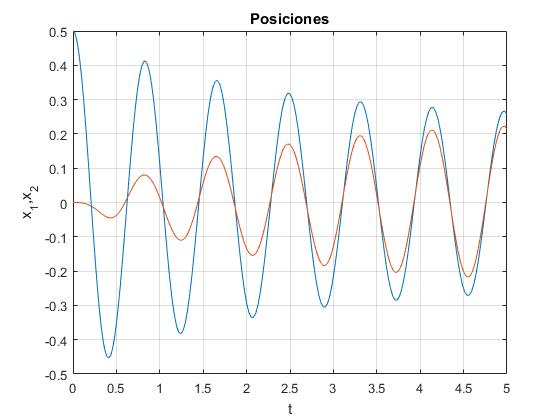
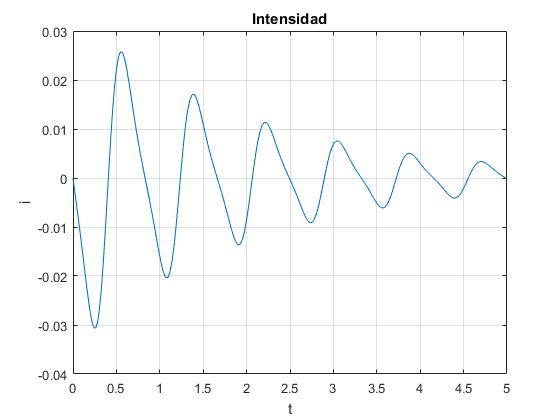
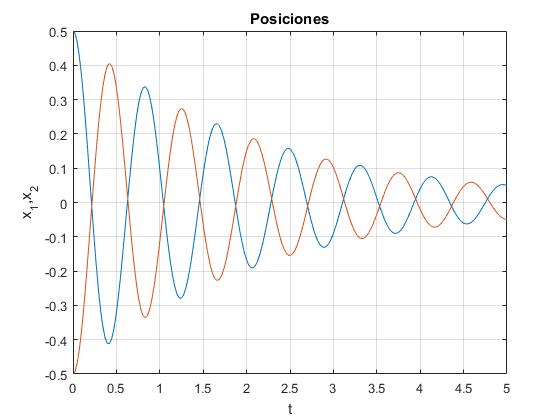
- Condiciones iniciales: x10=0.5, x20=0
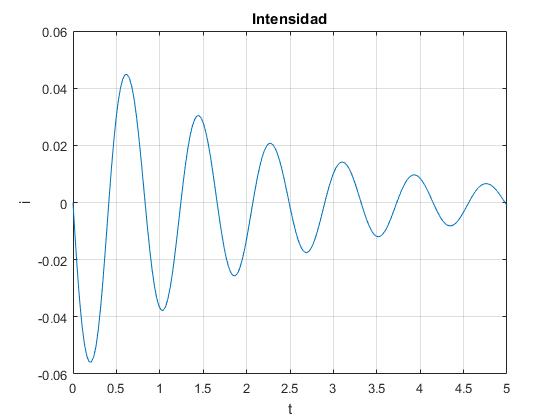
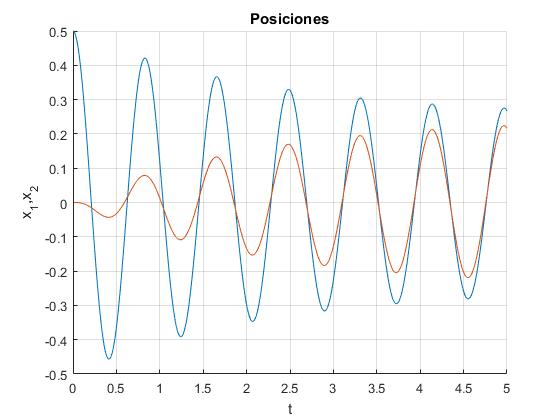
- Condiciones iniciales: x10=0.5, x20=-0.5
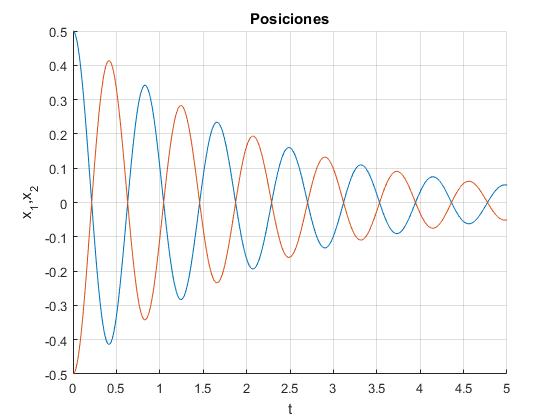
Desplazamiento x1 y x2 de los imanes en función del tiempo t
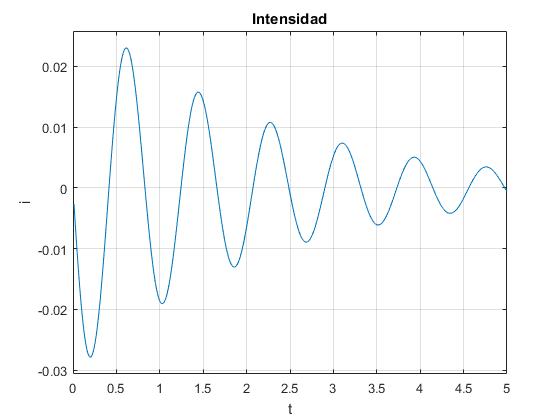
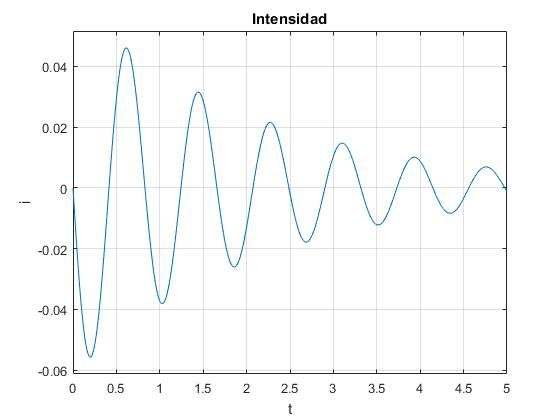
Intensidad i en función del tiempo t
Desplazamiento x1 y x2 de los imanes en función del tiempo t
Intensidad i en función del tiempo t.
Aproximaciones
Si los desplzamientos de los imanes x1 y x2 son pequeños frente a z10 y z10, el sistema de ecuaciones se reduce a
Si las alturas iniciales de los imanes z10=z20, el sistema de ecuaciones se reduce aún más
La intensidad que circula por las bobinas es
Este sistema de ecuaciones diferenciales tiene solución analítica, utilizaremos MATLAB Symbolic Toolbox para encontrarla con las siguientes condiciones iniciales: en el instante t=0, x1=x10, (dx1/dt)=0, x2=x20, (dx2/dt)=0.
syms x y w0 lambda x0 y0;
eq1='D2x+lambda*Dx-lambda*Dy+w0^2*x=0';
eq2='D2y-lambda*Dx+lambda*Dy+w0^2*y=0';
[x,y]=dsolve(eq1,eq2,'x(0)=x0','y(0)=y0','Dx(0)=0','Dy(0)=0');
N=10; %número de espiras
mu=2.6; %momento magnético del imán
sigma=2.741e7; %conductividad del cable
Di=0.15; %cm, sección del cable
a=1.5; %radio de la espira en cm
m=0.055; %masa del imán
k=3.17; %constante elástica
z0=1.7; %separación inicial entre el imán y la espira
cte=N*1e6*9*(4*pi*1e-7)^2*mu^2*sigma*Di^2*a^3*z0^2/(64*m*(a^2+z0^2)^5);
frec=sqrt(k/m);
%posiciones
xx=subs(x,{lambda,w0,x0,y0},{cte,frec,0.5,0});
yy=subs(y,{lambda,w0,x0,y0},{cte,frec,0.5,0});
%intensidad
cte=3*(4*pi*1e-7)*mu*sigma*Di^2*a*z0/(32*(a^2+z0^2)^(5/2));
inten=cte*(diff(xx)-diff(yy));
hold on
ezplot(xx,[0,5])
ezplot(yy,[0,5])
xlabel('t')
ylabel('x_1,x_2')
title('Posiciones')
hold off
figure
ezplot(inten,[0,5])
xlabel('t')
ylabel('i')
title('Intensidad')
- Condiciones iniciales: x10=0.5, x20=0
- Condiciones iniciales: x10=0.5, x20=-0.5
Desplazamiento x1 y x2 de los imanes en función del tiempo t
Intensidad i en función del tiempo t
Desplazamiento x1 y x2 de los imanes en función del tiempo t
La intensidad i en función del tiempo t
Actividades
Se introduce
- El desplazamiento inicial del imán izquierdo x10 en mm, en el control titulado Desplazamiento inicial del imán
- La separación inicial entre el imán y la bobina situados a la izquierda z10 en mm, en el control titulado Separación inicial imán-bobina.
- El desplazamiento inicial del imán derecho x20 en mm, en el control titulado Desplazamiento inicial del imán
- La separación inicial entre el imán y la bobina situados a la derecha z20 en mm, en el control titulado Separación inicial imán-bobina.
- El número de espiras N de las bobinas iguales, en el control tituado Número de espiras
El programa ha fijado los siguientes parámetros:
- Masa del imán, m= 55 g
- Momento magnético del imán, μ=2.6 Am2
- Radio de las espiras, a=15 mm
- Conductividad del material del que están hechas las espiras, σ=2.741·107 Ω-1m-1
- Diámetro de la sección del cable, D=1.5 mm
- Constante elástica del muelle, k=3.17 N/m
- Velocidades iniciales de los imanes, v10=0 y v20=0, parten del reposo
Se pulsa el botón titulado Nuevo.
Una circunferencia de radio a representa las espiras de la bobina, los puntos de color rojo representan los portadores de carga positiva, su movimiento nos da una idea del sentido de las corrientes inducidas en las espiras cuando se mueve el imán
La flecha situada a la izquierda del imán, representa la fuerza que ejercen las corrientes inducidas sobre el imán, se trata de una fuerza proporcional a la velocidad y de sentido contrario a la misma.
Activando la casilla titulada Gráfica y pulsando el botón titulado ► , vemos la representación gráfica de los desplazamientos de los imanes x1 (en color rojo) y x2 (en color azul), en la parte superior y la intensidad de la corriente en las bobinas, en la parte inferior
Referencias
G Donoso, C L Ladera, P Martín. Magnetically coupled magnet-spring oscillators. Eur. J. Phys. 31 (2010) 433-452

