Inducción homopolar
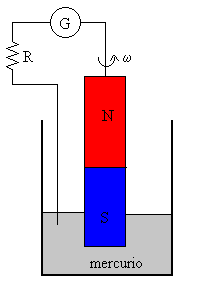
Poco después de descubrimiento de la inducción electromagnética, Faraday llevó a cabo el experimento cuyo esquema se muestra en la figura. Un imán cilíndrico se sostiene colgando verticalmente con uno de los polos sumergido en mercurio. El polo superior se conecta al mercurio mediante un cable. Si el imán se pone en movimiento de rotación, se observa el paso de corriente por el galvanómetro G.
Si se sustituye el galvanómetro por una batería que suministre corriente al circuito, el imán empieza a girar espontáneamente alrededor de su eje, tenemos entonces un motor.
La corriente inducida
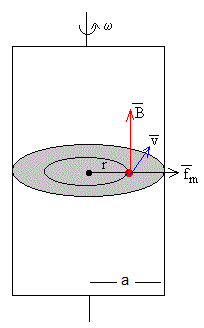
El campo en el interior del imán se dirige desde el polo Sur hacia el polo Norte y no cambia al girar el imán. Las líneas de fuerza en el interior del imán tienen una forma complicada por lo que nos limitaremos al estudio de un modelo más simple.
Consideremos un disco metálico de radio a, en rotación bajo la influencia de un campo magnético uniforme paralelo al eje del disco.
Explicaremos la aparición de la fem en términos de las fuerzas sobre los portadores de carga positivos del disco.
Consideremos un portador de carga positivo situado a una distancia r del disco. La velocidad del portador de carga es v=ω·r, cuya dirección es tangente a la circunferencia que describe. La fuerza que ejerce el campo magnético es
La fuerza magnética impulsa a los portadores de carga positivos desde el eje hacia el borde del disco. El campo (fuerza por unidad de carga) es En=v·B=B·ω ·r. La fem, o diferencia de potencial entre el borde del disco y el eje es
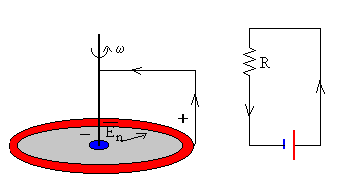
Los portadores de carga positiva son "impulsados" desde el eje hacia la periferia donde adquieren un potencial mayor. Luego, los portadores de carga "descienden espontáneamente" desde la periferia hacia el eje, completando el circuito.
La intensidad de la corriente inducida es el cociente entre la fem y la resistencia.
Momento de las fuerzas sobre el disco
Calcularemos el momento que tendremos que ejercer para que el disco se mueva con velocidad angular constante.
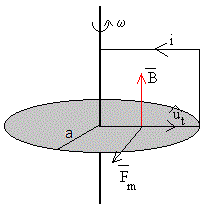
La fuerza que ejerce un campo magnético sobre una porción de corriente rectilínea de longitud L viene dada por la expresión
El vector unitarios señala el sentido de la corriente inducida
Lafuerza magnética sobre una porción de corriente rectilínea comprendida entre r y r+dr (el campo y la corriente son perpendiculares) es
dF=iBdr
El momento de todas estas fuerzas respecto del eje de rotación es
Este momento se opone al movimiento del disco, por lo que tendremos que aplicar una fuerza cuyo momento Ma sea igual y opuesto al momento M que ejerce el campo magnético sobre la corriente inducida.
El disco de Faraday tiene un comportamiento similar a la varilla que se mueve en un campo magnético uniforme. La diferencia está en el tipo de movimiento, rotación en el disco, traslación en la varilla, y las magnitudes que intervienen:
- momento y velocidad angular en el disco,
- fuerza y velocidad lineal en la varilla.
Balance energético
La energía por unidad de tiempo (potencia) mecánica aplicada es el producto del momento de la fuerza aplicada Ma por la velocidad angular constante ω .
Esta energía se disipa en la resistencia por efecto Joule
Actividades
Se introduce
- El campo magnético B (en gauss ó 10-4 T) que puede ser un número positivo o negativo, en el control titulado Campo magnético
- La velocidad angular, ω de rotación en (rad/s), un número positivo o negativo, en el control titulado Velocidad angular.
- Radio del disco a (en cm), en el control titulado Radio
Se pulsa el botón titulado Nuevo
Se observa el movimiento de rotación del disco.
Las corriente inducidas se visualizan mediante el movimiento de puntos de color rojo que representan a portadores de carga positivos.
Se representan los siguientes vectores
- Velocidad del portador de carga positivo (un vector de color negro tangente a la circunferencia que describe)
- Campo magnético (un vector de color azul que apunta hacia arriba o hacia abajo)
- Fuerza que ejerce el campo magnético sobre el portador de carga positivo (un vector de color rojo que apunta hacia la izquierda o hacia la derecha).
En la parte superior derecha, aparece el valor numérico de la fem, calculada mediante la fórmula
Generador homopolar
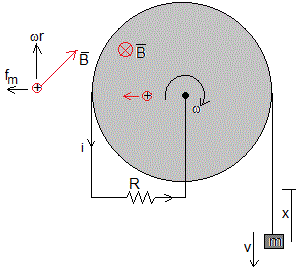
Un disco de radio a cuyo eje es horizontal, está en el seno de un campo magnético uniforme B perpendicular al plano del disco en el sentido indicado en la figura
La corriente generada en el disco circula por una resistencia R. Un cuerpo de masa m cuelga del borde del disco y lo acelera, hasta que alcanza una velocidad angular límite constante
Hemos calculado la corriente i a través de la resistencia
La energía por unidad de tiempo (potencia) disipada en la resistencia es
En un tiempo t el cuerpo cae una altura x, su energía potencial disminuye en mgx, la energía cinética aumenta en Iω2/2+mv2/2 y se disipa energía en la resistencia
La conservación de la energía se escribe
Integramos
Cuando t→∞, la velocidad angular de rotación, ω tiende hacia un valor límite constante
La intensidad límite constante es
La corriente generada por el disco produce el campo magnético
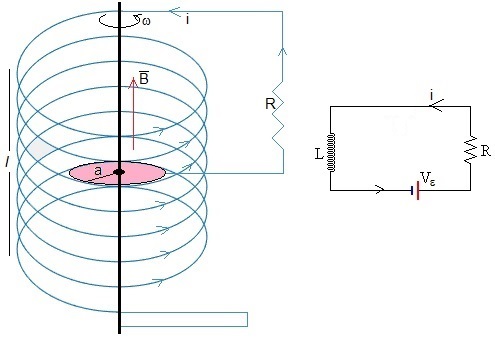
Se coloca el disco metálico de radio a en el interior de un solenoide largo de longitud l, sección S y de N espiras.
Se pone el disco en rotación con velocidad angular constante ω, la corriente inducida produce el campo magnético del solenoide, tal como se indica en la figura
La ecuación del circuito es
donde L es el coeficiente de autoinducción del solenoide
El campo magnético producido por un solenoide largo y de pequeña sección es,
En la sección anterior, hemos calculado la fem producida por el disco Vε. La ecuación del circuito se escribe en términos del número de espiras N, sección S, y longitud l del solenoide; de la velocidad angular de rotación del disco ω y resistencia R del circuito
Integramos, sabiendo que en el instante inicial t=0, la intensidad de la corriente vale i0
Si γ>0 la corriente crece, si γ<0 la corriente disminuye con el tiempo
Para que la corriente crezca, la velocidad angular del disco ω tiene que ser mayor que un valor mínimo
En la sección anterior, hemos calculado el momento que tenemos que aplicar Ma para mantener el disco girando con velocidad angular ω
Otra forma de obtener este resultado es la siguiente. En la unidad del tiempo, la energía mecánica, Maω
Una parte, se disipa en la resistencia, i2R
Otra, se almacena en la autoinducción en forma de campo magnético
El balance energético es
Referencias
Montgomery H. Unipolar induction: a neglected topic in the teaching of electromagnetism Eur. J. Phys. 20 (1999) pp. 271-280.
APhO Problems and Solutions, 2009 Thailand. A Self-excited Magnetic Dynamo
Sidney B. Cahn, Boris E. Nadgorny. A guide to physics problems, part 1. Mechanics, Relativity, and Electrodynamics.. Kluwer Academic Publishers, 2004. Problem 3.39

