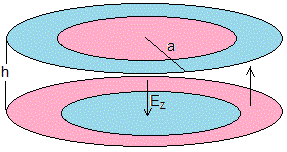
Consideremos un condensador plano-paralelo que consiste en dos placas circulares de radio a separadas una distancia h conectadas a un generador de corriente alterna

Supondremos que la separación h es mucho más pequeña que el radio de las placas a. En esta aproximación, la dirección del campo eléctrico es perpendicular a las placas y el campo eléctrico fuera de las placas puede considerarse despreciable

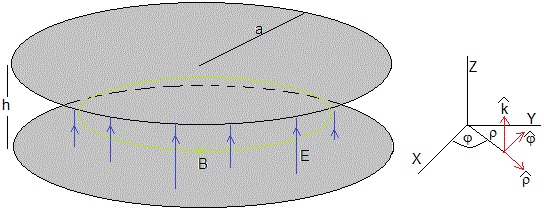
Adoptaremos coordenadas cilíndricas, dada la simetría del problema. El campo eléctrico tiene la dirección del eje Z, su amplitud depende de la distancia radial ρ y cambia con el tiempo de la forma

${\displaystyle \overrightarrow{E}\left(\rho ,t\right)=E_z\left(\rho \right)\cos \left(\omega t\right)\widehat{k}}$

E(ρ) es la amplitud del campo eléctrico, para ρ=0, E_z(0)=E₀.

ω es la fecuencia angular de la corriente alterna.

Ley de Faraday-Henry

Un campo magnético variable con el tiempo genera un campo eléctrico de acuerdo con la ley de Faraday-Henry, en forma diferencial

${\displaystyle \begin{array}{l}\nabla \times \overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}\\ \nabla \times \overrightarrow{E}=\left(\frac{1}{\rho }\frac{\partial E_z}{\partial \phi }-\frac{\partial E_{\phi }}{\partial z}\right)\widehat{\rho }+\left(\frac{\partial E_{\rho }}{\partial z}-\frac{\partial E_z}{\partial \rho }\right)\widehat{\phi }+\frac{1}{\rho }\left(\frac{\partial \left(\rho E_{\phi }\right)}{\partial \rho }-\frac{\partial E_{\rho }}{\partial \phi }\right)\widehat{k}\\ -\frac{\partial E_z}{\partial \rho }\cos \left(\omega t\right)\widehat{\phi }=-\frac{\partial B_{\rho }}{\partial t}\widehat{\rho }-\frac{\partial B_{\phi }}{\partial t}\widehat{\phi }-\frac{\partial B_z}{\partial t}\widehat{k}\\ \frac{d{E}_z}{d\rho }\cos \left(\omega t\right)=\frac{\partial B_{\phi }}{\partial t}\end{array}}$

Sabiendo que para t=0, B(ρ,0)=0, integramos

${\displaystyle \begin{array}{l}{B}_{\phi }\left(\rho ,t\right)={\displaystyle \underset{0}{\overset{t}{\int }}\frac{d{E}_z}{d\rho }\cos \left(\omega t\right)dt}\\ B_{\phi }\left(\rho ,t\right)=\frac{1}{\omega }\frac{d{E}_z}{d\rho }\sin \left(\omega t\right)\\ B_{\phi }\left(\rho ,t\right)=B\left(\rho \right)\sin \left(\omega t\right),B\left(\rho \right)=\frac{1}{\omega }\frac{\partial E_z}{\partial \rho }\end{array}}$

B(ρ) es la amplitud del campo magético. La dirección del campo magnético es la del vector unitario $\widehat{\phi }$

Ley de Ampère-Maxwell

${\displaystyle \nabla \times \overrightarrow{B}-\frac{1}{c^2}\frac{\partial \overrightarrow{E}}{\partial t}={\mu }_0\overrightarrow{J_m}}$

En ausencia de corrientes J_m debidas al movimiento de cargas en la materia

${\displaystyle \begin{array}{l}\nabla \times \overrightarrow{B}=\frac{1}{c^2}\frac{\partial \overrightarrow{E}}{\partial t}\\ \nabla \times \overrightarrow{B}=\left(\frac{1}{\rho }\frac{\partial B_z}{\partial \phi }-\frac{\partial B_{\phi }}{\partial z}\right)\widehat{\rho }+\left(\frac{\partial B_{\rho }}{\partial z}-\frac{\partial B_z}{\partial \rho }\right)\widehat{\phi }+\frac{1}{\rho }\left(\frac{\partial \left(\rho B_{\phi }\right)}{\partial \rho }-\frac{\partial B_{\rho }}{\partial \phi }\right)\widehat{k}\\ \frac{1}{\rho }\frac{\partial \left(\rho B_{\phi }\right)}{\partial \rho }\widehat{k}=-\frac{\omega }{c^2}\sin \left(\omega t\right)E_z\left(\rho \right)\widehat{k}\\ \frac{1}{\rho }\frac{d\left(\rho \frac{d{E}_z}{d\rho }\right)}{d\rho }\frac{1}{\omega }\sin \left(\omega t\right)=-\frac{\omega }{c^2}\sin \left(\omega t\right)E_z\left(\rho \right)\\ \frac{1}{\rho }\frac{d\left(\rho \frac{d{E}_z}{d\rho }\right)}{d\rho }+\frac{{\omega }^2}{c^2}{E}_z=0\\ \frac{d^2{E}_z}{d{\rho }^2}+\frac{1}{\rho }\frac{d{E}_z}{d\rho }+\frac{{\omega }^2}{c^2}{E}_z=0\\ {\rho }^2\frac{d^2{E}_z}{d{\rho }^2}+\rho \frac{d{E}_z}{d\rho }+\frac{{\omega }^2}{c^2}{\rho }^2{E}_z=0\end{array}}$

Campo eléctrico y campo magnético

Haciendo el cambio de variable

${\displaystyle \begin{array}{l}\rho =\frac{c}{\omega }\xi \\ {\xi }^2\frac{d^2{E}_z}{d{\xi }^2}+\xi \frac{d{E}_z}{d\xi }+{\xi }^2{E}_z=0\end{array}}$

que es una ecuación del tipo

${\displaystyle x^2\frac{d^{2}y}{d{x}^2}+x\frac{dy}{dx}+(x^2-n^2)y=0}$

con n=0. La solución es

${\displaystyle E_z\left(\xi \right)=A{J}_0(\xi )+B{Y}_0(\xi )}$

Se descarta el segundo término, ya que Y₀(ξ)→∞ cuando ξ→0.

El coeficiente A se determina sabiendo que E_z(0)=E₀

${\displaystyle \begin{array}{l}{E}_z\left(0\right)=A{J}_0(0)\\ A=E_0\end{array}}$

La expresión de la amplitud del campo eléctrico E_z(ρ) es

${\displaystyle E_z\left(\frac{\omega }{c}\rho \right)=E_0{J}_0\left(\frac{\omega }{c}\rho \right)}$

Teniendo en cuenta la relación

${\displaystyle \frac{d{J}_n(k)}{dk}=n\frac{J_n(k)}{k}-J_{n+1}(k)}$

La amplitud del campo magnético es

${\displaystyle \begin{array}{l}{B}_{\phi }\left(\rho \right)=\frac{1}{\omega }\frac{d\left(E_z\left(\rho \right)\right)}{d\rho }=\frac{E_0}{\omega }\frac{d\left(J_0\left(\frac{\omega }{c}\rho \right)\right)}{d\rho }=-\frac{1}{\omega }{E}_0\frac{\omega }{c}{J}_1\left(\frac{\omega }{c}\rho \right)\\ B_{\phi }\left(\rho \right)=-\frac{1}{c}{E}_0{J}_1\left(\frac{\omega }{c}\rho \right)\end{array}}$

Como J₁(0)=0, para ρ=0, entonces B_φ(0)=0 y

${\displaystyle {\left(\frac{d{E}_z\left(\rho \right)}{d\rho }\right)}_{\rho =0}=0}$

El campo eléctrico vale E₀ para ρ=0, pero su derivada con respecto a ρ es nula

Energía asocida al campo eléctrico

La expresión del los campo eléctrico es

${\displaystyle E_z\left(\rho ,t\right)=E_0{J}_0\left(\frac{\omega }{c}\rho \right)\cos \left(\omega t\right)}$

La energía por unidad de volumen es

${\displaystyle u_E=\frac{1}{2}{\epsilon }_0{E}^2}$

Para calcular la energía en el volumen del condensador (πa²h), tomamos una capa cilíndrica de radio ρ altura h y espesor dρ

${\displaystyle U_E={\displaystyle \underset{0}{\overset{a}{\int }}\left(\frac{1}{2}{\epsilon }_0{E}_0^2{J}_0^2\left(\frac{\omega }{c}\rho \right){\cos }^2\left(\omega t\right)\right)}\left(2\pi \rho ·d\rho \right)h=\pi {\epsilon }_{0}h{E}_0^2{\cos }^2\left(\omega t\right){\displaystyle \underset{0}{\overset{a}{\int }}\rho J_0^2\left(\frac{\omega }{c}\rho \right)d\rho }}$

Buscamos la solución de esta integral en la fórmula 5.14.5 página 129 del libro N. N. Lebedev. Special Functions and their Applications. Prentice-Hall (1965)

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{a}{\int }}x{J}_n^2}\left(kx\right)dx=\frac{a^2}{2}\left[{\left(\frac{d{J}_n\left(ka\right)}{dk}\right)}^2+\left(1-\frac{n^2}{k^2{a}^2}{J}_n^2\left(ka\right)\right)\right]\\ {\displaystyle \underset{0}{\overset{1}{\int }}x{J}_n^2(kx)dx}=\frac{1}{2}\left[{\left(\frac{d{J}_n(k)}{dk}\right)}^2+\left(1-\frac{n^2}{k^2}\right)J_n^2(k)\right]\end{array}}$

Teniendo en cuenta que

${\displaystyle \frac{d{J}_0(k)}{dk}=-J_1(k)}$

Efectuando el cambio de variable

${\displaystyle \begin{array}{l}x=\frac{\rho }{a}\\ {\displaystyle \underset{0}{\overset{a}{\int }}\rho J_0^2\left(\frac{\omega }{c}\rho \right)d\rho }=a^2{\displaystyle \underset{0}{\overset{1}{\int }}x{J}_0^2\left(\frac{\omega a}{c}x\right)dx}=\frac{a^2}{2}\left[J_1^2\left(\frac{\omega a}{c}\right)+J_0^2\left(\frac{\omega a}{c}\right)\right]\end{array}}$

>> syms k x;
>> int(x*besselj(0,k*x)^2,x,0,1)
ans =besselj(0, k)^2/2 + besselj(1, k)^2/2 

La energía asociada al campo eléctrico en el condensador es

${\displaystyle U_E=\frac{1}{2}{\epsilon }_0{E}_0^2\left(\pi a^{2}h\right)\left[J_1^2\left(\frac{\omega a}{c}\right)+J_0^2\left(\frac{\omega a}{c}\right)\right]{\cos }^2\left(\omega t\right)}$

Energía asocida al campo magnético

La expresión del los campo magnético es

${\displaystyle B_{\phi }\left(\rho ,t\right)=-\frac{1}{c}{E}_0{J}_1\left(\frac{\omega }{c}\rho \right)\sin \left(\omega t\right)}$

La energía por unidad de volumen es

${\displaystyle u_B=\frac{1}{2{\mu }_0}{B}^2,c=\frac{1}{\sqrt{{\epsilon }_0{\mu }_0}}}$

Para calcular la energía en el volumen del condensador (πa²h), tomamos una capa cilíndrica de radio ρ altura h y espesor dρ

${\displaystyle U_B={\displaystyle \underset{0}{\overset{a}{\int }}\left(\frac{1}{2}{\epsilon }_0{E}_0^2{J}_1^2\left(\frac{\omega }{c}\rho \right){\sin }^2\left(\omega t\right)\right)}\left(2\pi \rho ·d\rho \right)h=\pi {\epsilon }_{0}h{E}_0^2{\sin }^2\left(\omega t\right){\displaystyle \underset{0}{\overset{a}{\int }}\rho J_1^2\left(\frac{\omega }{c}\rho \right)d\rho }}$

Para calcular la derivada de dJ_n(k)/dk, utilizamos la fórmula alternativa

${\displaystyle \begin{array}{l}\frac{d{J}_n(k)}{dk}=J_{n-1}(k)-\frac{n}{k}{J}_n(k)\\ {\displaystyle \underset{0}{\overset{1}{\int }}x{J}_1^2(kx)dx}=\frac{1}{2}\left[{\left(J_0(k)-\frac{J_1(k)}{k}\right)}^2+\left(1-\frac{1}{k^2}\right)J_1^2(k)\right]=\frac{1}{2}\left[J_0^2(k)+J_1^2(k)-\frac{2}{k}{J}_0(k)J_1(k)\right]\end{array}}$

>> syms k x;
>> int(x*besselj(1,k*x)^2,x,0,1)
ans =besselj(0, k)^2/2 + besselj(1, k)^2/2 - (besselj(0, k)*besselj(1, k))/k

Efectuando el cambio de variable

${\displaystyle {\displaystyle \underset{0}{\overset{a}{\int }}\rho J_1^2\left(\frac{\omega }{c}\rho \right)d\rho }=a^2{\displaystyle \underset{0}{\overset{1}{\int }}x{J}_1^2\left(\frac{\omega a}{c}x\right)dx}=\frac{a^2}{2}\left[J_0^2\left(\frac{\omega a}{c}\right)+J_1^2\left(\frac{\omega a}{c}\right)-\frac{2c}{\omega a}{J}_0\left(\frac{\omega a}{c}\right)J_1\left(\frac{\omega a}{c}\right)\right]}$

La energía asociada al campo magnético en el condensador es

${\displaystyle U_B=\frac{1}{2}{\epsilon }_0{E}_0^2\left(\pi a^{2}h\right)\left[J_0^2\left(\frac{\omega a}{c}\right)+J_1^2\left(\frac{\omega a}{c}\right)-\frac{2c}{\omega a}{J}_0\left(\frac{\omega a}{c}\right)J_1\left(\frac{\omega a}{c}\right)\right]{\sin }^2\left(\omega t\right)}$

Energía asociada al campo electromagnético

La suma de ambas contribuciones es

${\displaystyle U=U_E+U_B=\frac{1}{2}{\epsilon }_0{E}_0^2\left(\pi a^{2}h\right)\left[J_1^2\left(\frac{\omega a}{c}\right)+J_0^2\left(\frac{\omega a}{c}\right)-\frac{2c}{\omega a}{J}_0\left(\frac{\omega a}{c}\right)J_1\left(\frac{\omega a}{c}\right){\sin }^2\left(\omega t\right)\right]}$

La energía electromagnética dentro del condensador varía con el tiempo, sus valores máximo y mínimo son, respectivamente

${\displaystyle \begin{array}{l}{U}_{máx}=\frac{1}{2}{\epsilon }_0{E}_0^2\left(\pi a^{2}h\right)\left[J_1^2\left(\frac{\omega a}{c}\right)+J_0^2\left(\frac{\omega a}{c}\right)\right]\\ U_{mín}=\frac{1}{2}{\epsilon }_0{E}_0^2\left(\pi a^{2}h\right)\left[J_1^2\left(\frac{\omega a}{c}\right)+J_0^2\left(\frac{\omega a}{c}\right)-\frac{2c}{\omega a}{J}_0\left(\frac{\omega a}{c}\right)J_1\left(\frac{\omega a}{c}\right)\right]\end{array}}$

Las energía electromagnética U depende del parámetro ωa/c. Hay valores específicos de ω que hacen que la energía electromagnética almacenada en el condensador sea constante (independiente del tiempo). Esas frecuencias son aquellas que hacen que J₀(ωa/c)=0 o J₁(ωa/c)=0

Calculamos las primeras raíces de las ecuaciones J₀(x)=0 y J₁(x)=0

function condensador_9
    x=linspace(0,20,10);
    f=@(x) besselj(0,x);
    rr=raices(f,x); 
    disp('J_0(x)')
    disp( rr)
    
    f=@(x) besselj(1,x);
     rr=raices(f,x); 
    disp('J_1(x)')
    disp (rr)

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

J_0(x)
    2.4048    5.5201    8.6537   11.7915   14.9309   18.071
J_1(x)
    3.8317    7.0156   10.1735   13.3237   16.4706   19.6159

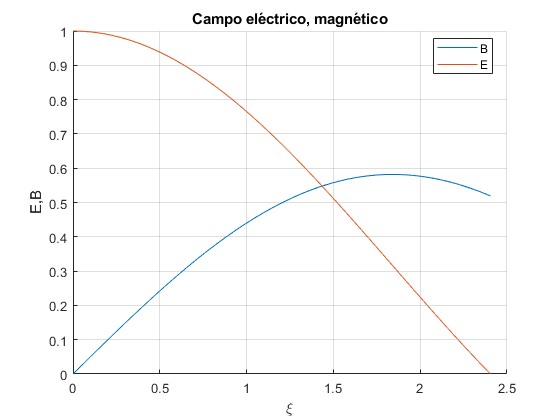
• Para las frecuencias tales que ωa/c=2.4048, 5.5201, 8.6537... la amplitud del campo eléctrico E_z es nula en el borde de la placa circular ρ=a. La energía electromagnética es

${\displaystyle U=\frac{1}{2}{\epsilon }_0{E}_0^2\left(\pi a^{2}h\right)J_1^2\left(\frac{\omega a}{c}\right)}$

• Para las frecuencias tales que ωa/c=3.8317, 7.0156, 10.1735... la amplitud del campo magnético B_φ es nula en el borde de la placa circular ρ=a. La energía electromagnética es

${\displaystyle U=\frac{1}{2}{\epsilon }_0{E}_0^2\left(\pi a^{2}h\right)J_0^2\left(\frac{\omega a}{c}\right)}$

Gráficas

• Representamos la amplitud del campo eléctrico, E_z(ρ)/E₀ y la amplitud del campo magnético, B_φ(ρ)/B₀ para la frecuencia ω=2.4048c/a en función de ξ=ωρ/c. Donde B₀ =-E₀/c

hold on
fplot(@(x) besselj(1,x),[0,2.4048]) %campo B
fplot(@(x) besselj(0,x),[0,2.4048]) %campo E
hold off
grid on
xlabel('\xi')
legend('B','E','Location', 'best')
ylabel('E,B')
title('Campo eléctrico, magnético')



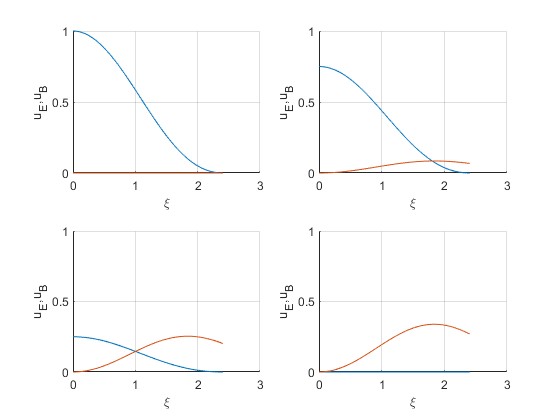
Representamos la densidad de energía eléctrica $\frac{u_E}{\frac{1}{2}{\epsilon }_0{E}_0^2}$ en función de ξ en los instantes ωt=0, π/6, π/3, π/2.

T=[0,pi/6,pi/3, pi/2];
for k=1:4
    subplot(2,2,k)
    hold on
    fplot(@(x) besselj(0,x).^2*cos(T(k))^2,[0,2.4048]) %campo E
    fplot(@(x) besselj(1,x).^2*sin(T(k))^2,[0,2.4048]) %campo B
    hold off
    grid on
    ylim([0,1]);
    xlabel('\xi')
    ylabel('u_E,u_B')
end



• Representamos la amplitud del campo eléctrico, E_z(ρ)/E₀ y la amplitud del campo magnético, B_φ(ρ)/B₀ para la frecuencia ω=3.8317c/a en función de ξ=ωρ/c. Donde B₀ =-E₀/c

hold on
fplot(@(x) besselj(1,x),[0,3.8317]) %campo B
fplot(@(x) besselj(0,x),[0,3.8317]) %campo E
hold off
grid on
xlabel('\xi')
ylabel('E,B')
legend('B','E','Location', 'best')
title('Campo eléctrico, magnético')





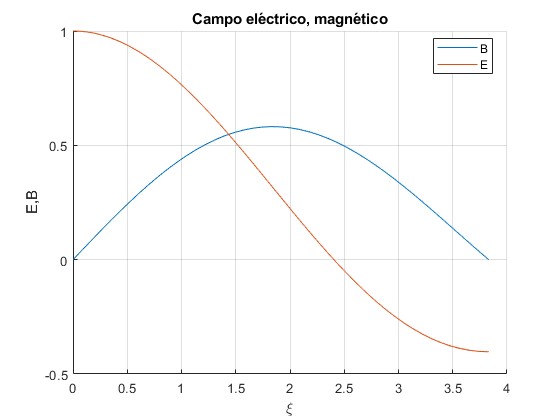
El campo eléctrico se invierte para ξ>2.4048. La placa circular esta dividida en dos zonas un círculo de radio ξ=2.4048 con carga de un signo y un anillo cuya carga es de signo contrario

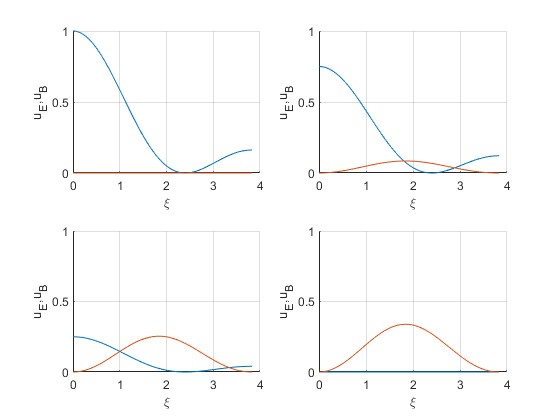
Representamos la densidad de energía magnética $\frac{u_B}{\frac{1}{2}{\epsilon }_0{E}_0^2}$ en función de ξ en los instantes ωt=0, π/6, π/3, π/2.

T=[0,pi/6,pi/3, pi/2];
for k=1:4
    subplot(2,2,k)
    hold on
    fplot(@(x) besselj(0,x).^2*cos(T(k))^2,[0,3.8317]) %campo E
    fplot(@(x) besselj(1,x).^2*sin(T(k))^2,[0,3.8317]) %campo B
    hold off
    grid on
    ylim([0,1]);
    xlabel('\xi')
    ylabel('u_E,u_B')
end

Variación de la energía electromagnética con el tiempo

Supongamos un volumen V limitado por una superficie S, se cumple que

${\displaystyle {\displaystyle \underset{S}{\int }\frac{1}{{\mu }_0}\left(\overrightarrow{E}\times \overrightarrow{B}\right)}·\overrightarrow{dS}=-\frac{\partial }{\partial t}{\displaystyle \underset{V}{\int }\left(\frac{1}{2}{\epsilon }_0{E}^2+\frac{1}{2{\mu }_0}{B}^2\right)}dV}$

La integral del segundo miembro es la suma de las densidades de energía eléctrica y magnética u=u_E+u_B. El segundo miembro, es la energía perdida por unidad de tiempo en el volumen V que será igual al flujo de energía hacia el exterior a través de la superficie S.

En forma diferencial y en coordenadas cilíndricas, se escribe

${\displaystyle \begin{array}{l}\frac{\partial u}{\partial t}+\nabla ·\overrightarrow{S}=0\\ \frac{\partial u}{\partial t}+\left(\frac{1}{\rho }\frac{\partial \left(\rho S_{\rho }\right)}{\partial \rho }+\frac{1}{\rho }\frac{\partial S_{\phi }}{\partial \phi }+\frac{\partial S_z}{\partial z}\right)=\mathrm{0,}\end{array}}$

Se denomina vector de Poynting

${\displaystyle \begin{array}{l}\overrightarrow{S}=\frac{\overrightarrow{E}\times \overrightarrow{B}}{{\mu }_0}=\frac{1}{{\mu }_0}\left|\begin{array}{ccc}\widehat{\rho }& \widehat{\phi }& \widehat{k}\\ 0& 0& E_z\\ 0& B_{\phi }& 0\end{array}\right|=-\frac{E_z{B}_{\phi }}{{\mu }_{0}c}\widehat{\rho }=\frac{E_0^2}{{\mu }_{0}c}{J}_0\left(\frac{\omega }{c}\rho \right)J_1\left(\frac{\omega }{c}\rho \right)\cos \left(\omega t\right)\sin \left(\omega t\right)\widehat{\rho }=\\ \overrightarrow{S}=\frac{1}{2}{\epsilon }_{0}c{E}_0^2{J}_0\left(\frac{\omega }{c}\rho \right)J_1\left(\frac{\omega }{c}\rho \right)\sin \left(2\omega t\right)\widehat{\rho }\end{array}}$

El vector de Poynting tiene dirección radial, es perpendicular a la superficie lateral cilíndica, unas veces apunta hacia dentro y otras hacia fuera, oscilando a una frecuencia 2ω

Comprobamos que la suma de los dos términos da cero

Primer término

${\displaystyle \begin{array}{l}u=u_E+u_B=\frac{1}{2}{\epsilon }_0{E}_0^2{J}_0^2\left(\frac{\omega }{c}\rho \right){\cos }^2\left(\omega t\right)+\frac{1}{2{\mu }_0}\frac{1}{c^2}{E}_0^2{J}_1^2\left(\frac{\omega }{c}\rho \right){\sin }^2\left(\omega t\right)=\\ \frac{1}{2}{\epsilon }_0{E}_0^2\left(J_0^2\left(\frac{\omega }{c}\rho \right){\cos }^2\left(\omega t\right)+J_1^2\left(\frac{\omega }{c}\rho \right){\sin }^2\left(\omega t\right)\right)\\ \frac{\partial u}{\partial t}={\epsilon }_0{E}_0^2\omega \left(-J_0^2\left(\frac{\omega }{c}\rho \right)\cos \left(\omega t\right)\sin \left(\omega t\right)+J_1^2\left(\frac{\omega }{c}\rho \right)\sin \left(\omega t\right)\cos \left(\omega t\right)\right)=\\ \frac{1}{2}{\epsilon }_0{E}_0^2\omega \left(-J_0^2\left(\frac{\omega }{c}\rho \right)+J_1^2\left(\frac{\omega }{c}\rho \right)\right)\sin \left(2\omega t\right)\end{array}}$

Segundo término

Utilizando las derivadas

${\displaystyle \begin{array}{l}\frac{d{J}_0(k)}{dk}=-J_1(k)\\ \frac{d{J}_1(k)}{dk}=J_0(k)-\frac{1}{k}{J}_1(k)\end{array}}$

obtenemos

${\displaystyle \begin{array}{l}\frac{1}{\rho }\frac{d\left(\rho S_{\rho }\right)}{d\rho }=\frac{1}{\rho }\frac{d}{d\rho }\left(\rho \frac{1}{2}{\epsilon }_{0}c{E}_0^2{J}_0\left(\frac{\omega }{c}\rho \right)J_1\left(\frac{\omega }{c}\rho \right)\sin \left(2\omega t\right)\right)=\\ =\frac{1}{2}{\epsilon }_{0}c{E}_0^2\sin \left(2\omega t\right)\frac{1}{\rho }\frac{d}{d\rho }\left(\rho J_0\left(\frac{\omega }{c}\rho \right)J_1\left(\frac{\omega }{c}\rho \right)\right)\\ \frac{1}{2}{\epsilon }_{0}c{E}_0^2\sin \left(2\omega t\right)\left[\frac{1}{\rho }{J}_0\left(\frac{\omega }{c}\rho \right)J_1\left(\frac{\omega }{c}\rho \right)-\frac{\omega }{c}{J}_1^2\left(\frac{\omega }{c}\rho \right)+\frac{\omega }{c}{J}_0\left(\frac{\omega }{c}\rho \right)\left(J_0\left(\frac{\omega }{c}\rho \right)-\frac{c}{\omega \rho }{J}_1\left(\frac{\omega }{c}\rho \right)\right)\right]=\\ \frac{1}{2}{\epsilon }_0{E}_0^2\omega \left[-J_1^2\left(\frac{\omega }{c}\rho \right)+J_0^2\left(\frac{\omega }{c}\rho \right)\right]\sin \left(2\omega t\right)\end{array}}$

Referencias

A Beléndez, J J Sirvent-Verdú, T Lloret, J C García-Vázquez, R Ramírez-Vázquez, S Marini. Capacitor connected to an alternating voltage: Maxwell’s equations, Poynting’s theorem and oscillating L-C circuits. Eur. J. Phys. 45 (2024) 045201