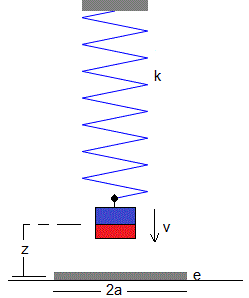
Sea un muelle de constante k suspendido verticalmente. Se cuelga de su extremo libre inferior un potente imán de momento magnético μ. A una distancia z=z₀ por debajo del imán se coloca una placa metálica de radio a y espesor e y de conductividad σ. Supondremos que el espesor e es muy pequeño comparado con la distancia del imán a la placa.

Al moverse el imán, el campo magnético variable induce corrientes de Foucault en la placa metálica. Dichas corrientes establecen una fuerza sobre el imán que se opone a su velocidad. Observaremos oscilaciones cuya amplitud va decreciendo con el tiempo.

Corrientes inducidas en la placa

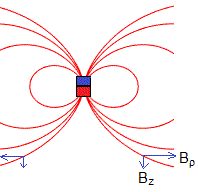
En la página, Campo magnético producido por una imán hemos supuesto que un imán se comporta como un dipolo magnético de momento μ. Las componentes del campo son

${\displaystyle \begin{array}{l}{B}_{\rho }=\frac{{\mu }_0\mu }{4\pi }\frac{3\rho z}{{\left({\rho }^2+z^2\right)}^{5/2}}\hfill \\ B_z=\frac{{\mu }_0\mu }{4\pi }\frac{2z^2-{\rho }^2}{{\left({\rho }^2+z^2\right)}^{5/2}}=\frac{{\mu }_0\mu }{4\pi }\left\{\frac{3z^2}{{\left({\rho }^2+z^2\right)}^{5/2}}-\frac{1}{{\left({\rho }^2+z^2\right)}^{3/2}}\right\}\hfill \end{array}}$

El flujo del campo producido por el imán a través de una espira de radio r es.

${\displaystyle \Phi =\underset{S}{{\displaystyle \int }}\overrightarrow{B}\cdot \overrightarrow{dS}=\underset{S}{{\displaystyle \int }}(B_{\rho }\widehat{j}+B_z\widehat{k})\cdot dS·\widehat{k}=-\underset{S}{{\displaystyle \int }}{B}_z·dS}$

El flujo depende solamente de la componente B_z del campo magnético

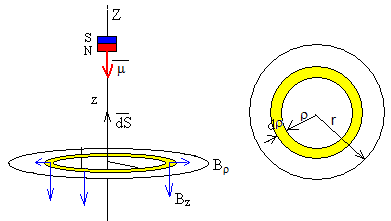
El elemento diferencial de superficie dS, es el área de un anillo de radio ρ y de espesor dρ, su valor es dS=2πρ·dρ

${\displaystyle \begin{array}{l}\Phi =-{\displaystyle \underset{0}{\overset{r}{\int }}\frac{{\mu }_0·\mu }{4\pi }\left(\frac{3z^2}{{\left(\sqrt{{\rho }^2+z^2}\right)}^5}-\frac{1}{{\left(\sqrt{{\rho }^2+z^2}\right)}^3}\right)2\pi \rho ·d\rho }\\ \Phi =-\frac{{\mu }_0·\mu }{4}\left(3z^2{\displaystyle \underset{0}{\overset{r}{\int }}\frac{2\rho ·d\rho }{{\left(\sqrt{{\rho }^2+z^2}\right)}^5}-}{\displaystyle \underset{0}{\overset{r}{\int }}\frac{2\rho ·d\rho }{{\left(\sqrt{{\rho }^2+z^2}\right)}^3}}\right)=-\frac{{\mu }_0\mu ·r^2}{2{\left(\sqrt{r^2+z^2}\right)}^3}\end{array}}$

Aplicando la ley de Faraday

${\displaystyle V_{\epsilon }=-\frac{d\Phi }{dt}=-\frac{d\Phi }{dz}\frac{dz}{dt}=-\frac{d\Phi }{dz}(-v)=\frac{3{\mu }_0\mu r^2}{2}\frac{zv}{{\left(r^2+z^2\right)}^{5/2}}}$

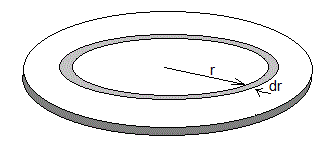
Consideremos una porción de placa, un anillo de radio r anchura dr y espesor e tal como se muestra en la figura.

Calculamos la intensidad di de la corriente que circula por este anillo

Sea σ la conductividad del material del que está hecho el tubo, y dA=e·dr el área de la sección trasversal del anillo de longitud 2πr. La resistencia del anillo es

${\displaystyle \frac{1}{\sigma }\frac{2\pi r}{e·dr}}$

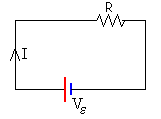
Ley de Ohm para este anillo se escribe

${\displaystyle \begin{array}{l}{V}_{\epsilon }=di\frac{1}{\sigma }\frac{2\pi r}{e·dr}\\ di=\frac{V_{\epsilon }\sigma }{2\pi r}e·dr\end{array}}$

La fuerza que ejerce el campo magnético producido por el imán sobre la corriente inducida di en el anillo es

${\displaystyle \overrightarrow{dF}=di({\widehat{u}}_t\times \overrightarrow{B})(2\pi r)}$

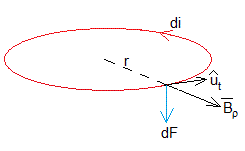
La componente B_ρ del campo magnético ejerce una fuerza a lo largo del eje Z y la componente B_z ejerce una fuerza a lo largo de la dirección radial que no tiene efecto alguno sobre la placa. El módulo de la fuerza a lo largo del eje Z es

${\displaystyle \begin{array}{l}dF=\left(2\pi r\right)B_{\rho }di=\left(2\pi r\right)\frac{{\mu }_0\mu }{4\pi }\frac{3rz}{{\left(\sqrt{z^2+r^2}\right)}^5}di\\ =\frac{9{\mu }_0^2{\mu }^2}{8\pi }\frac{\sigma ev{r}^3{z}^2}{{(z^2+r^2)}^5}dr\end{array}}$

Aplicando la tercera ley de Newton, esta es la fuerza que la corriente inducida ejerce sobre el imán. La fuerza total se obtiene integrando

${\displaystyle F=\frac{9{\mu }_0^2{\mu }^2}{8\pi }\sigma ev{z}^2{\displaystyle \underset{0}{\overset{a}{\int }}\frac{r^3}{{(z^2+r^2)}^5}dr}}$

La integral es sencilla de resolver

${\displaystyle F=\frac{3{\mu }^2{\mu }_0^2}{64\pi }\frac{\sigma e}{z^4}\left(1-\frac{1+4u^2}{{\left(1+u^2\right)}^4}\right)v}$

Con u=a/z. Representamos las función

${\displaystyle f(u)=1-\frac{1+4u^2}{{\left(1+u^2\right)}^4}}$

f=@(x) 1-(1+4*x^2)/(1+x^2)^4;
fplot(f,[0,4])
grid on
xlabel('a/z')
ylabel('f(a/z)')

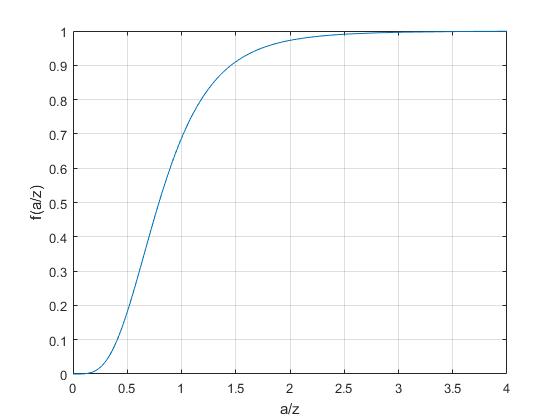
Si el radio a de la placa es muy grande comparado con la distancia z entre la placa y el imán, la expresión de la fuerza en el límite cuando u→∞ es

${\displaystyle F=\left(\frac{3{\mu }^2{\mu }_0^2}{64\pi }\frac{\sigma e}{z^4}\right)v}$

Ecuación del movimiento

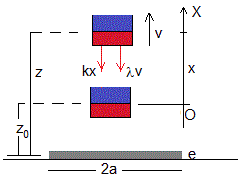
La fuerza que se opone al movimiento del imán es proporcional a la velocidad v y de sentido contrario.

Sea z₀ la altura inicial del imán sobre la placa metálica. Cuando el imán se desplaza x=z-z₀ de la posición de equilibrio las fuerzas que actúan sobre el imán son:

• La fuerza que ejerce el muelle deformado kx, siendo k es la constante del muelle
• La fuerza λv que ejercen las corrientes de Foucault generadas en la placa metálica sobre el imán, donde λ es una función de z

La ecuación del movimiento del imán es

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=-\lambda \frac{dx}{dt}-kx\\ \frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}+{\omega }_0^{2}x=0\end{array}}$

Integramos la ecuación diferencial con las condiciones iniciales siguientes: en el instante t=0, la posición del imán es x₀ y su velocidad es v=0.

Oscilaciones amortiguadas

En una primera aproximación, vamos a suponer que la fuerza F=λv que ejercen las corrientes inducidas sobre el imán, no cambia con la altura z del imán, de modo que λ es constante e igual a

${\displaystyle \lambda =\frac{3{\mu }^2{\mu }_0^2}{64\pi }\frac{\sigma e}{z_0^4}}$

Siendo z₀, la separación inicial de equilibrio. La solución de la ecuación diferencial con las condiciones iniciales: en el instante t=0, la posición inicial es x=x₀ y la velocidad inicial es v₀ es (véase Oscilaciones amortiguadas)

${\displaystyle \begin{array}{l}\omega =\sqrt{{\omega }_0^2-{\gamma }^2}\\ x=\exp (-\gamma t)\left(\frac{v_0+\gamma x_0}{\omega }\sin (\omega t)+x_0\cos (\omega t)\right)\end{array}}$

Caso general

En el caso general, λ y por tanto, γ es una función de la separación z=z₀+x entre el imán y la placa metálica.

${\displaystyle \lambda =\frac{3{\mu }^2{\mu }_0^2}{64\pi }\frac{\sigma e}{z^4}\left(1-\frac{1+4u^2}{{\left(1+u^2\right)}^4}\right)}$

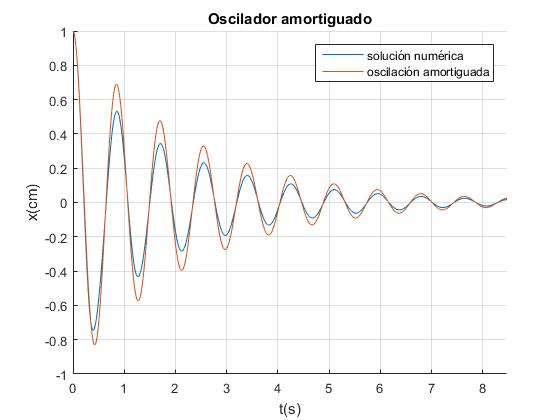
Donde u=a/z. Resolvemos la ecuación diferencial por procedimientos numéricos con las condiciones iniciales: en el instante t=0, la posición inicial es x=x₀ y la velocidad inicial es v₀. Representamos el desplazamiento x del imán en función del tiempo t, en color rojo la aproximación con λ constante, en color azul la solución numérica con γ función de la separación z. Se han tomado del artículo mencionado en las referencias, los siguientes valores de los parámetros:

• Constante elástica del muelle, k=3.3 N/m
• Masa del imán, m=60 g
• Momento magnético del imán, μ=2.6 Am²
• Radio de la placa, a=75 mm
• Conductividad del material del que está hecho la placa, σ=2.741·10⁷ Ω^-1m^-1
• Espesor de la placa, e=1 mm
• Separación inicial entre el imán en equilibrio y la placa, z₀=17 mm
• El imán se separa x₀=5 mm de la posición de equilibrio y se suelta
• Velocidad inicial del imán, v₀=0, parte del reposo

m=60/1000; %masa del imán
k=3.3; %constante elástica
mu=2.6; %Am2, momento magnético
sigma=2.741e7; %conductividad
e=1/10; %espesor en cm
z0=17/10; %separación inicial en cm
a=75/10; %radio placa en cm
w0=sqrt(k/m); %frecuencia angular propia
gg=3*(4*pi*1e-7)^2*mu^2*sigma*e*1e6/(64*pi*2*m); %rozamiento, gamma,
x0=[5/10,0];  %condiciones iniciales:
 [posición inical en cm, velocidad inicial]
tspan=[0 10*2*pi/w0];  %diez periodos

%solución numérica
f=@(t,x) [x(2);-2*gg*x(2)*(1/(z0+x(1))^4-(z0+x(1))^2*((z0+x(1))^2+4*a^2)
/((z0+x(1))^2+a^2)^4)-w0*w0*x(1)]; 
[t,x]=ode45(f,tspan,x0);

%oscilaciones amortiguadas
g=gg/z0^4;
w=sqrt(w0^2-g^2);
xx=@(t) exp(-g*t)*((x0(2)+g*x0(1))*sin(w*t)/w+x0(1)*cos(w*t));

hold on
plot(t,x(:,1))
fplot(xx,tspan)
hold off
legend('solución numérica','oscilación amortiguada')
xlabel('t(s)')
ylabel('x(cm)');
title('Oscilador amortiguado')
grid on

Actividades

Se introduce

• El desplazamiento inicial del imán x₀ en mm, en el control titulado Desplazamiento inicial del imán
• La separación inicial entre el imán y la placa circular conductora z₀ en mm, en el control titulado Separación inicial imán-placa.
• El radio de la placa a en mm, en el control de edición titulado Radio de la placa

El programa ha fijado los siguientes parámetros:

• Masa del imán, m= 60 g
• Momento magnético del imán, μ=2.6 Am²
• Conductividad del material del que está hecho la placa, σ=2.741·10⁷ Ω^-1m^-1
• Espesor de la placa, e=1 mm
• Constante elástica del muelle, k=3.3 N/m
• Velocidad inicial del imán, v₀=0, parte del reposo

Se pulsa el botón titulado Nuevo.

La placa conductora está representada por un círculo de color gris que se ve parcialmente en la simulación si su radio a es grande. Dentro de la placa señalamos una circunferencia de radio r, los puntos de color rojo representan los portadores de carga positiva, su movimiento nos da una idea del sentido de las corrientes inducidas en la placa cuando se mueve el imán

La flecha situada a la izquierda del imán, representa la fuerza que ejercen las corrientes inducidas sobre el imán, se trata de una fuerza proporcional a la velocidad y de sentido contrario a la misma.

Placa metálica indefinida con un orificio de radio a

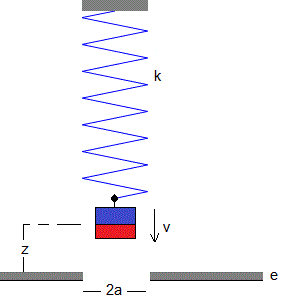
Consideremos ahora una placa indefinida de espesor e que tiene un orificio de radio a, tal como se muestra en la figura.

La fuerza que ejercen las corrientes inducidas sobre el imán se calcula integrando la expresión de la fuerza sobre un elemento de corriente entre a e ∞

${\displaystyle F=\frac{9{\mu }^2{\mu }_0^2}{8\pi }\sigma ec{z}^2{\displaystyle \underset{a}{\overset{\infty }{\int }}\frac{r^3}{{\left(z^2+r^2\right)}^5}}dr}$

Para calcular la integral se hace el cambio de variable x=r² y a continuación, se integra por partes. El resultado es

${\displaystyle F=\frac{3{\mu }^2{\mu }_0^2}{64\pi }\sigma e\frac{z^2\left(z^2+4a^2\right)}{{\left(z^2+a^2\right)}^4}v=\frac{3{\mu }^2{\mu }_0^2}{64\pi }\frac{\sigma e}{z^4}\frac{\left(1+4u^2\right)}{{\left(1+u^2\right)}^4}v}$

Con u=a/z. Representamos las función

${\displaystyle f(u)=\frac{\left(1+4u^2\right)}{{\left(1+u^2\right)}^4}}$

f=@(x)(1+4*x^2)/(1+x^2)^4;
fplot(f,[0,4])
grid on
xlabel('a/z')
ylabel('f(a/z)')

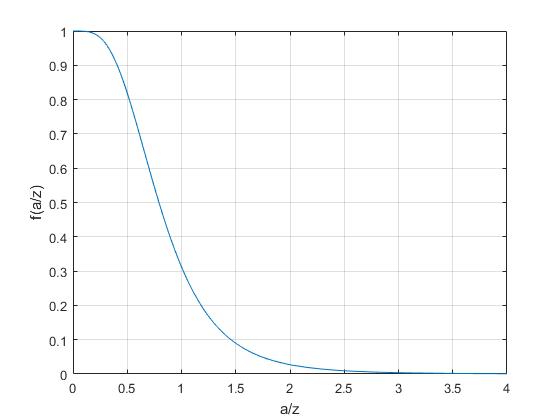
Cuando el radio a del orificio en la placa conductora es grande la función f(u) alcanza el valor límite 0. La fuerza que ejercen las corrientes inducidas es muy pequeña y las oscilaciones del imán unido al muelle son libres. Cuando el orificio es muy pequeño obtenemos la misma expresión para la fuerza F de rozamiento que en la sección anterior cuando consideramos que la placa tenía un radio a muy grande

Ecuación del movimiento

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=-\lambda \frac{dx}{dt}-kx\\ \lambda =\frac{3{\mu }^2{\mu }_0^2}{64\pi }\sigma e\frac{z^2\left(z^2+4a^2\right)}{{\left(z^2+a^2\right)}^4}\end{array}}$

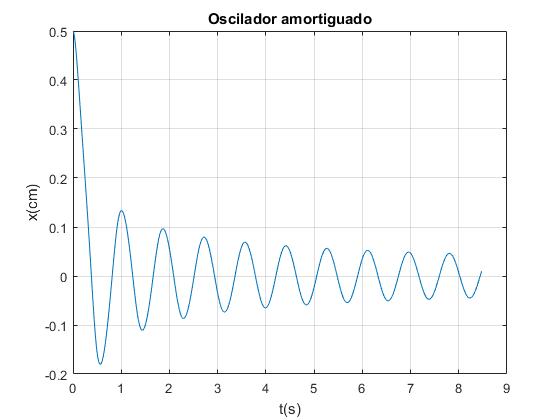
Con z=z₀+x. Resolvemos la ecuación diferencial por procedimientos numéricos con las condiciones iniciales: en el instante t=0, la posición inicial es x=x₀ y la velocidad inicial es v₀. Representamos el desplazamiento x del imán en función del tiempo t. Los valores de los parámetros son:

• Constante elástica del muelle, k=3.3 N/m
• Masa del imán, m=60 g
• Momento magnético del imán, μ=2.6 Am²
• Radio del orificio, a=75 mm
• Conductividad del material del que está hecho la placa, σ=2.741·10⁷ Ω^-1m^-1
• Espesor de la placa, e=1 mm
• Separación inicial entre el imán en equilibrio y la placa, z₀=0
• El imán se separa x₀=5 mm de la posición de equilibrio y se suelta
• Velocidad inicial del imán, v₀=0, parte del reposo

m=60/1000; %masa del imán
k=3.3; %constante elástica
mu=2.6; %Am2, momento magnético
sigma=2.741e7; %conductividad
e=1/10; %espesor en cm
z0=0; %separación inicial en cm
a=7/10; %radio del orificio en cm
w0=sqrt(k/m); %frecuencia angular propia
gg=3*(4*pi*1e-7)^2*mu^2*sigma*e*1e6/(64*pi*2*m); %rozamiento, gamma,
x0=[5/10,0];  %condiciones iniciales: 
[posición inical en cm, velocidad inicial]
tspan=[0 10*2*pi/w0];  %diez periodos

%solución numérica
f=@(t,x) [x(2);-2*gg*x(2)*((z0+x(1))^2*((z0+x(1))^2+4*a^2)
/((z0+x(1))^2+a^2)^4)-w0*w0*x(1)]; 
[t,x]=ode45(f,tspan,x0);

plot(t,x(:,1))
xlabel('t(s)')
ylabel('x(cm)');
title('Oscilador amortiguado')
grid on

Referencias

C L Ladera, G Donoso. Oscillations of a spring-magnet system damped by a conductive plate. Eur. J. Phys. 34 (2013) 1187-1197

Celso L. Ladera, Guillermo Donoso, Pablo Martín. Spring-magnet oscillations through a bored conductive plate. Lat. Am. Phys. Educ. Vol 8, No. 1, March 2014, 109-117