Las corrientes de Foucault
Demostración en el aula: el péndulo de Waltenhofen
Cuando se coloca una pieza de metal en un campo magnético variable con el tiempo se genera un campo eléctrico que produce un movimiento de las cargas libres en el conductor metálico, generando corrientes.
Estas corrientes disipan energía en el metal en forma de calor.
Cuando una pieza de metal se mueve en una región en la que existe un campo magnético no uniforme pero constante en el tiempo se generan corrientes y la energía se disipa en el conductor metálico. Este fenómeno se puede explicar por medio de la fuerza de Lorentz. A causa de la disipación de la energía se produce una fuerza de frenado que disminuye la velocidad de la pieza metálica.
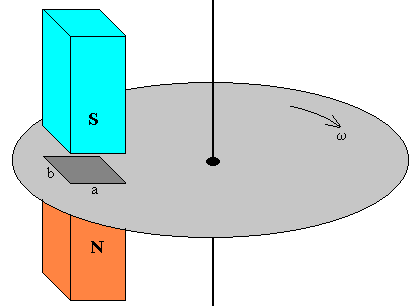
En esta página, daremos una descripción cualitativa de las corrientes de Foucault, teniendo presente el comportamiento de una espira que atraviesa una región en la que existe un campo magnético uniforme con velocidad constante. A continuación, mediante un modelo simple se demostrará que la fuerza de frenado es proporcional a la velocidad de la pieza metálica, concluyendo con un programa interactivo, que muestra los efectos de la fuerza de frenado en un disco en rotación como el que se muestra en la figura.
Movimiento de una pieza conductora hacia y desde un campo magnético uniforme
El efecto de las corrientes de Foucault es una disipación de la energía por efecto Joule. Estas pérdidas se intentarán reducir al máximo posible en los núcleos de un transformador, pero puede ser interesante aumentarlas para realizar un frenado electromagnético (amortiguamiento, freno eléctrico) o en la producción del calor (horno de inducción).
El comportamiento de una pieza metálica rectangular que se mueve hacia o sale de una región donde existe un campo magnético uniforme es esencialmente el mismo que el de una espira que se mueve hacia o sale de una región donde existe un campo magnético uniforme perpendicular a la espira.
Se introduce la pieza rectangular
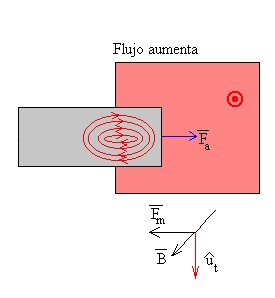
Cuando se introduce la pieza rectangular en la región donde existe un campo magnético uniforme, el flujo crece con el tiempo y las corrientes en torbellino se oponen al incremento de flujo. La fuerza que ejerce el campo magnético sobre cada una de las corrientes inducidas da una resultante que se opone a la fuerza aplicada.
El campo magnético es perpendicular al plano del dibujo y está dirigido hacia el lector. El sentido de la corriente inducida en la región donde existe campo magnético está indicada por el vector unitario
Se retira la pieza rectangular
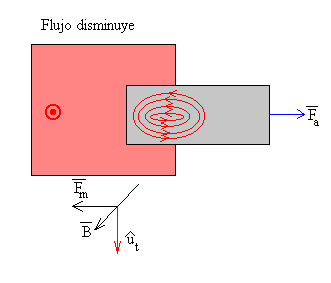
Cuando se retira la pieza rectangular de la región donde existe un campo magnético uniforme, el flujo decerece con el tiempo y las corrientes en torbellino se oponen a dicha disminución. La fuerza que ejerce el campo magnético sobre cada una de las corrientes inducidas da una resultante que se opone a la fuerza aplicada.
Del mismo modo que hemos visto en la espira que se introduce en el campo magnético, la corriente se genera en el lado de la espira que está en el interior del campo magnético y retorna por la parte de la espira que está fuera de dicha región.
Pieza metálica grande
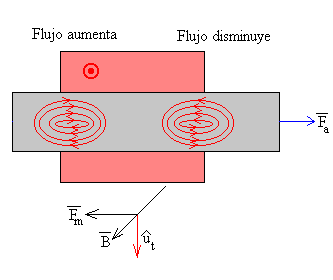
Consideremos ahora que la pieza metálica es más grande que la región que contiene el campo magnético. Se forman dos corrientes en forma de torbellino de sentidos contrarios, una a la izquierda y otra a la derecha en los límites de la región rectangular donde existe el campo magnético. La fuerza que ejerce el campo magnético sobre las corrientes inducidas es de sentido contrario a la fuerza aplicada que mueve la pieza hacia la derecha.
Disco que se mueve en un campo magnético uniforme
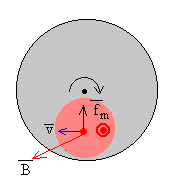
Consideremos un disco que se mueve en un campo magnético uniforme perpendicular al plano del disco, pero limitado a una porción de su superficie. Tenemos ahora una doble corriente en forma de torbellino, que circula en sentidos contrarios, en el borde anterior y posterior del campo magnético.
Explicamos el origen de las corrientes inducidas a partir de la fuerza sobre los portadores de carga positiva situados en la región donde existe campo magnético.
donde v es la velocidad de los portadores situados a una distancia r del eje del disco v=ω r.
Aunque los portadores de carga experimentan una fuerza más intensa en el borde del disco que los situados hacia el centro, la intensidad de la corriente inducida es proporcional a la velocidad angular ω del disco. La intensidad es también proporcional al campo magnético B.
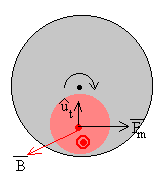
Las fuerzas que ejerce el campo magnético sobre las porciones de corriente inducida
se oponen todas al movimiento del disco y son proporcionales a la intensidad de la corriente i y al campo magnético B aplicado. Por tanto, estas fuerzas serán proporcionales a la velocidad angular ω de rotación del disco y a B2, el cuadrado del módulo del campo magnético aplicado.
El momento de dichas fuerzas respecto del eje del disco, como se ha señalado, es proporcional a la velocidad angular del disco, Mm=kω
Donde k es una constante que depende de la conductividad del material del que está hecho el disco, la intensidad del campo magnético y la posición y tamaño de la porción de la superficie del disco sobre la que actúa el campo magnético.
Una situación análoga al movimiento vertical de una varilla en un seno de un campo magnético uniforme.
Ecuación de la dinámica de rotación
Supongamos un disco de momento de inercia I0 que se le proporciona una velocidad angular ω0 en el instante inicial. La velocidad angular del disco en el instante t se obtiene a partir de la ecuación de la dinámica de rotación
La velocidad angular disminuye exponencialmente con el tiempo.
El péndulo de Pohl es un disco que puede oscilar angularmente gracias al momento que ejerce sobre el mismo un muelle helicoidal. Un dispositivo de este tipo describe oscilaciones libres. Si al disco se le acopla un anillo de metal (normalmente cobre) y se le hace girar entre los polos un electroimán tenemos un modelo de oscilador amortiguado.

Dependiendo de la intensidad de la corriente en el electroimán, el campo puede ser mayor o menor. El momento de la fuerza de frenado magnético puede hacerse suficientemente grande de modo que el sistema deje de oscilar, estamos en el caso de las oscilaciones críticas y sobreamortiguadas.
Actividades
Se introduce
- El campo magnético (en gauss ó 10-4 T) que puede ser un número positivo o negativo
- La velocidad angular inicial de rotación en (rad/s) un número positivo o negativo.
Se pulsa el botón titulado Nuevo.
Se observa el movimiento de rotación del disco, como va disminuyendo su velocidad angular.
Las corriente inducidas se visualizan mediante el movimiento de puntos de color rojo que representan a portadores de carga positivos. Las corrientes inducidas se originan en la región en la que existe campo magnético y se cierran por fuera de dicha región tal como vimos en el movimiento de una espira en el seno de un campo magnético uniforme.
Los vectores representan:
- Sentido de la corriente inducida (un vector hacia arriba o hacia abajo de color rojo)
- Campo magnético (un vector de color azul perpendicular a la pantalla, hacia el lector o en sentido contrario a éste)
- Resultante de las fuerzas sobre las porciones de corriente inducida situadas en la región donde existe campo magnético (un vector de color negro, siempre opuesto a la velocidad del disco)
A la derecha, se representa la velocidad angular en función del tiempo y se observa que se trata de una exponencial decreciente.

