Campo eléctrico generado por un campo magnético variable con el tiempo

Un solenoide muy largo de longitud l, radio a y N vueltas conduce una corriente i que aumenta con el tiempo, di/dt>0.

Vamos a obtener el valor del campo eléctrico generado para los puntos que distan del eje del solenoide r<a y para r>a

Aplicando la ley de Ampère, deducimos el campo magnético producido por un solenoide de longitud l y con N espiras.

${\displaystyle B=\frac{{\mu }_{0}N}{l}i}$

El campo en el interior del solenoide es constante y paralelo al eje del solenoide. El campo en el exterior del solenoide es nulo

La ley de Faraday es

${\displaystyle {\displaystyle \oint \overrightarrow{E}·\overrightarrow{dl}}=-\frac{d}{dt}{\displaystyle \underset{S}{\int }\overrightarrow{B}·\overrightarrow{dS}}}$

1. Para los puntos que distan del eje del solenoide r<a



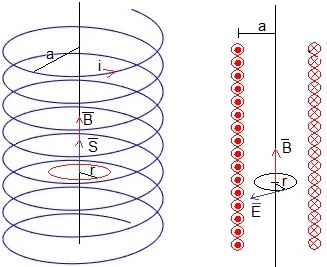
El flujo a través de un camino circular de radio r<a es

${\displaystyle {\displaystyle \underset{S}{\int }\overrightarrow{B}·\overrightarrow{dS}}=\left(\frac{{\mu }_{0}N}{l}i\right)\left(\pi r^2\right)\cos 0=\pi r^2\frac{{\mu }_{0}N}{l}i}$

La derivada del flujo, respecto del tiempo t, cambiada de signo es

${\displaystyle -\frac{d}{dt}{\displaystyle \underset{S}{\int }\overrightarrow{B}·\overrightarrow{dS}}=-\pi r^2\frac{{\mu }_{0}N}{l}\frac{di}{dt}}$



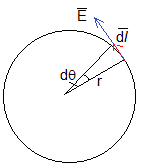
El problema tiene simetría cilíndrica por lo que el módulo del campo eléctrico es constante en todos los puntos que distan r del eje. La circulación del campo eléctrico es

${\displaystyle {\displaystyle \oint \overrightarrow{E}·\overrightarrow{dl}}={\displaystyle \oint E\left(r·d\theta \right)\cos 0=Er{\displaystyle \oint d\theta =}}2\pi rE}$

Igualando los dos miembros de la ley de Faraday

${\displaystyle \begin{array}{l}2\pi rE=-\pi r^2\frac{{\mu }_{0}N}{l}\frac{di}{dt}\\ E=-\frac{{\mu }_{0}N}{2l}\frac{di}{dt}r\end{array}}$

2. Para los puntos que distan del eje del solenoide r>a



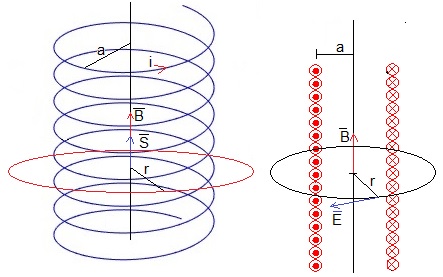
El flujo a través de un camino circular de radio r>a es

${\displaystyle {\displaystyle \underset{S}{\int }\overrightarrow{B}·\overrightarrow{dS}}=\left(\frac{{\mu }_{0}N}{l}i\right)\left(\pi a^2\right)\cos 0=\pi a^2\frac{{\mu }_{0}N}{l}i}$

La derivada del flujo, respecto del tiempo t, cambiada de signo es

${\displaystyle -\frac{d}{dt}{\displaystyle \underset{S}{\int }\overrightarrow{B}·\overrightarrow{dS}}=-\pi a^2\frac{{\mu }_{0}N}{l}\frac{di}{dt}}$

Igualando los dos miembros de la ley de Faraday

${\displaystyle \begin{array}{l}2\pi rE=-\pi a^2\frac{{\mu }_{0}N}{l}\frac{di}{dt}\\ E=-\frac{{\mu }_{0}N}{2l}\frac{di}{dt}\frac{a^2}{r}\end{array}}$

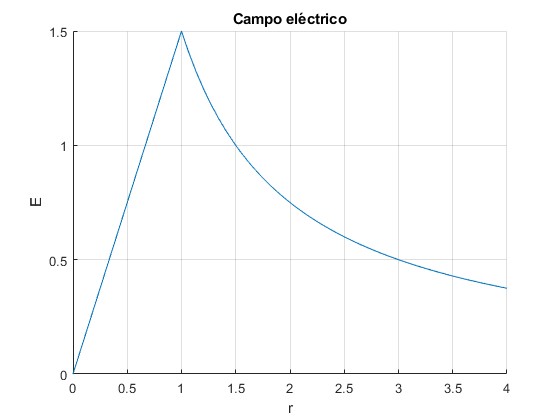
Representamos el módulo del campo eléctrico en función de la distancia radial al eje del solenoide

k=1.5; %constante
a=1; %radio del solenoide
hold on
line([0,a],[0,k*a])
fplot(@(r) k*a^2./r,[a,4*a])
hold off
grid on
xlabel('r')
ylabel('E')
title('Campo eléctrico')

Si se sustituye el camino circular de radio r por una espira conductora del mismo radio, se genera una corriente inducida en la espira

Cilindro cargado en el seno de un campo magnético variable con el tiempo

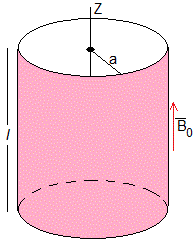
Un cilindro de longitud l y radio a, puede girar sin rozamiento alrededor del eje vertical Z, su momento de inercia es I respecto de dicho eje. La superficie lateral está uniformemente cargada con σ C/m².

Se sitúa el cilindro en el seno de un campo magnético B uniforme paralelo al eje Z, pero que disminuye con el tiempo, hasta que se anula. En el instante inicial t=0, el campo magnético vale B₀

Vamos a determinar la velocidad angular final del cilindro

Ley de Faraday

${\displaystyle {\displaystyle \oint \overrightarrow{E}·\overrightarrow{dl}}=-\frac{d}{dt}{\displaystyle \underset{S}{\int }\overrightarrow{B}·\overrightarrow{dS}}}$

El flujo a través de un camino circular de radio r=a es

${\displaystyle {\displaystyle \underset{S}{\int }\overrightarrow{B}·\overrightarrow{dS}}=B\left(\pi a^2\right)\cos 0=\pi a^{2}B}$

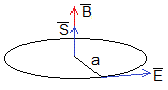
La derivada del flujo cambiada de signo es

${\displaystyle -\frac{d}{dt}{\displaystyle \underset{S}{\int }\overrightarrow{B}·\overrightarrow{dS}}=-\pi a^2\frac{dB}{dt}=\pi a^2\left|\frac{dB}{dt}\right|}$

El problema tiene simetría cilíndrica por lo que el módulo del campo eléctrico es constante en todos los puntos que distan a del eje. La circulación del campo eléctrico es

${\displaystyle {\displaystyle \oint \overrightarrow{E}·\overrightarrow{dl}}={\displaystyle \oint E\left(a·d\theta \right)\cos 0=Ea{\displaystyle \oint d\theta =}}2\pi aE}$

Igualando los dos miembros de la ley de Faraday

${\displaystyle \begin{array}{l}2\pi aE=\pi a^2\left|\frac{dB}{dt}\right|\\ E=\frac{a}{2}\left|\frac{dB}{dt}\right|\end{array}}$

Como B disminuye con el tiempo, el campo eléctrico tiene el sentido indicado en la figura

Ecuación del movimiento

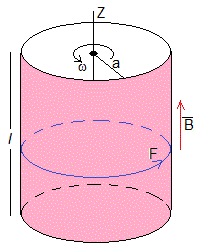
El campo eléctrico ejerce una fuerza sobre los portadores de carga situados en la superficie lateral del cilindro

${\displaystyle F=E\sigma \left(2\pi al\right)=\sigma \pi a^2\left|\frac{dB}{dt}\right|l}$

Esta fuerza ejerce un momento Fa respecto del eje de rotación que hace que el cilindro gire con velocidad angular ω. La ecuación del movimiento del cilindro es

${\displaystyle I\frac{d\omega }{dt}=\sigma \pi a^3\left|\frac{dB}{dt}\right|l}$

Eliminado dt e integrando

${\displaystyle \begin{array}{l}d\omega =\frac{\sigma \pi a^{3}l}{I}dB\\ \omega =\frac{\sigma \pi a^{3}l}{I}\left(B_0-B_f\right)\end{array}}$

Campo magnético final

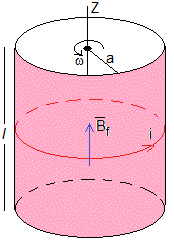
El campo magnético externo se ha anulado y el cilindro ha alcanzado la velocidad angular ω, final

Calculamos el campo magnético final producido por las cargas situadas en la superficie lateral del cilindro, sabiendo que la velocidad angular final es ω

Una carga que gira es equivalente a una intensidad igual al cociente entre la carga y el periodo T o tiempo que tarda en dar una vuelta.

${\displaystyle i=\frac{\sigma \left(2\pi al\right)}{T}=\frac{2\pi \sigma al}{\frac{2\pi }{\omega }}=\sigma al\omega }$

Recordamos que el campo magnético producido por un solenoide es

${\displaystyle B={\mu }_0\frac{Ni}{l}}$

El campo en el interior del solenoide es constante y paralelo al eje del solenoide. El campo en el exterior del solenoide es nulo

La intensidad i=σalω, es equivalente a la intenidad Ni que recorre la superficie lateral de un solenoide de la misma longitud. Por tanto, el campo magnético final producido por el cilindro cargado que gira es

${\displaystyle B_f={\mu }_0\frac{\sigma al\omega }{l}={\mu }_0\sigma a\omega }$

La velocidad angular final es

${\displaystyle \begin{array}{l}\omega =\frac{\sigma \pi a^{3}l}{I}\left(B_0-{\mu }_0\sigma a\omega \right)\\ \left(I+{\mu }_0{\sigma }^2\pi a^{4}l\right)\omega =\sigma \pi a^{3}l{B}_0\\ \omega =\frac{\sigma \pi a^{3}l}{I+{\mu }_0{\sigma }^2\pi a^{4}l}{B}_0\end{array}}$

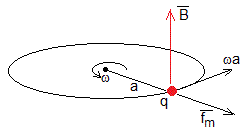
El campo magnético exterior B ejerce una fuerza $\overrightarrow{f_m}=q\overrightarrow{v}\times \overrightarrow{B}$ sobre los portadores de carga situados en la superficie lateral del cilindro en movimiento de rotación. Pero esta fuerza, como vemos en la figura, tiene dirección radial y no afecta al movimiento de rotación del cilindro

Placa metálica que cuelga de un muelle, que oscila en el seno de un campo magnético

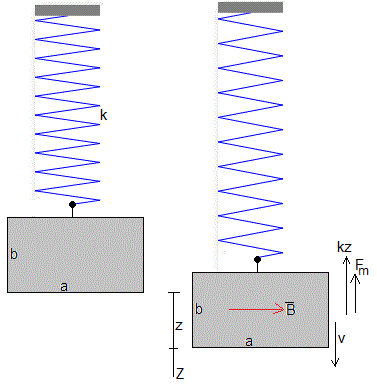
Una placa de cobre de masa m, de lados a y b y de espesor d, está sujeta al extremo libre de un muelle elástico de constante k. La placa se encuentra en una región donde hay un campo magnético B uniforme paralelo a la placa. Vamos a deducir la ecuación del movimiento de la placa.

Cuando colgamos la placa, el muelle se deforma z₀, de modo que kz₀=mg

En esta posición de equilibrio establecemos el origen. Cuando la placa se desplaza z, la fuerza sobre la placa es -kz además, el campo magnético ejerce una fuerza F_m sobre los portadores de carga que vamos a determinar

En el instante t, la posición de la placa es z y su velocidad es v=dz/dt

El campo magnético ejerce una fuerza sobre los portadores de carga

${\displaystyle \overrightarrow{F}=q\overrightarrow{v}\times \overrightarrow{B}}$

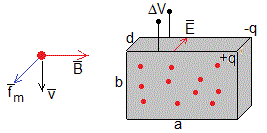
El módulo de la fuerza es f_m=qvB

Entre las dos caras de la placa se establece un campo eléctrico E=f_m/q=vB, uniforme, y una diferencia de potencial ΔV=Ed=vBd.

Tenemos un condensador plano-paralelo cargado cuya capacidad es

${\displaystyle C=\frac{{\epsilon }_{0}ab}{d}}$

La carga del condensador es

${\displaystyle q=C·\Delta V=\frac{{\epsilon }_{0}ab}{d}vBd={\epsilon }_{0}abB·v}$

La energía del condensador cargado es

${\displaystyle U=\frac{1}{2}C·\Delta V^2=\frac{1}{2}\frac{{\epsilon }_{0}ab}{d}{\left(vBd\right)}^2=\frac{1}{2}{\epsilon }_0\left(abd\right)B^2·v^2}$

La fuerza asociada con esta energía potencial es

${\displaystyle \begin{array}{l}{F}_m=-\frac{dU}{dz}=-{\epsilon }_0\left(abd\right)B^2·v\frac{dv}{dz}=-{\epsilon }_0\left(abd\right)B^2·v\frac{dv}{dt}\frac{dt}{dz}\\ F_m=-{\epsilon }_0\left(abd\right)B^2\frac{dv}{dt}\end{array}}$

Alternativamente, tenemos una corriente de longitud d y sección ab entre las dos caras de la placa, de intensidad i=dq/dt.

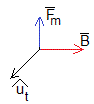
La fuerza que ejerce el campo magnético sobre la porción l de corriente rectilínea es

${\displaystyle \overrightarrow{F}=i\left(\widehat{u_t}\times \overrightarrow{B}\right)l}$

El módulo de la fuerza es, F_m=iBd, de sentido contrario a la velocidad v=dz/dt

La intensidd i es

${\displaystyle i=\frac{dq}{dt}={\epsilon }_{0}abB·\frac{dv}{dt}}$

El módulo de la fuerza que se opone a la velocidad de la placa

${\displaystyle F_m=iBd={\epsilon }_{0}abB·\frac{dv}{dt}Bd={\epsilon }_0\left(abd\right)B^2\frac{dv}{dt}}$

Obtenemos el mismo resultado

Ecuación del movimiento

La ecuación del movimiento de la placa es

${\displaystyle \begin{array}{l}m\frac{dv}{dt}=-kz-{\epsilon }_0\left(abd\right)B^2\frac{dv}{dt}\\ \left(m+{\epsilon }_0\left(abd\right)B^2\right)\frac{dv}{dt}+kz=0\\ \frac{d^{2}z}{d{t}^2}+\frac{k}{M}z=\mathrm{0,}{\omega }_0^2=\frac{k}{m+{\epsilon }_0\left(abd\right)B^2}\end{array}}$

La placa describe un movimiento armónico simple, de frecuencia angular ω₀

${\displaystyle z=A\sin \left({\omega }_{0}t+\phi \right)}$

La amplitud A y la fase φ se determinan a partir de las condiciones iniciales.

El cociente

${\displaystyle \frac{{\epsilon }_0\left(abd\right)B^2}{m}=\frac{{\epsilon }_0\left(abd\right)B^2}{{\rho }_{Cu}\left(abd\right)}=\frac{{\epsilon }_0{B}^2}{{\rho }_{Cu}}}$

es muy pequeño. 1/(4πε₀)=9·10⁹, B=0.1 T, densidad del cobre ρ_Cu=8.93·10³ kg/m³. El resultado es 9.9014·10^-18

Energía por unidad de tiempo disipada

La energía por unidad de tiempo disipada es

${\displaystyle \begin{array}{l}P=i^{2}R={\left({\epsilon }_{0}abB·\frac{dv}{dt}\right)}^2\rho \frac{d}{ab}\\ P=i^{2}R={\left({\epsilon }_{0}abB·\frac{dv}{dt}\right)}^2\rho \frac{d}{ab}={\epsilon }_0^2\rho B^2\left(abd\right){\left(-{\omega }_0^{2}A\sin \left({\omega }_{0}t+\phi \right)\right)}^2\end{array}}$

La resistencia de una placa R=ρd/(ab), donde ρ es la resistividad del material (cobre), d la longitud del conductor y ab la sección

El valor medio es

${\displaystyle <P>={\epsilon }_0^2\rho B^2\left(abd\right){\omega }_0^4{A}^2<{\sin }^2\left({\omega }_{0}t+\phi \right)>=\frac{1}{2}{\epsilon }_0^2\rho B^2\left(abd\right){\omega }_0^4{A}^2}$

La resistividad del cobre es ρ=1.75·10^-8 Ω·m, y con el dato de ε₀ elevado al cuadrado, el valor medio <P> es muy pequeño

Referencias

Solutions of Indian National Physics Olympiad – 2020. Problem 2, pp. 3-4

Physics Challenge for Teachers and Students. Solution April 2012 Challenge. Spring vibes. The Physics Teacher, 50 (2012)