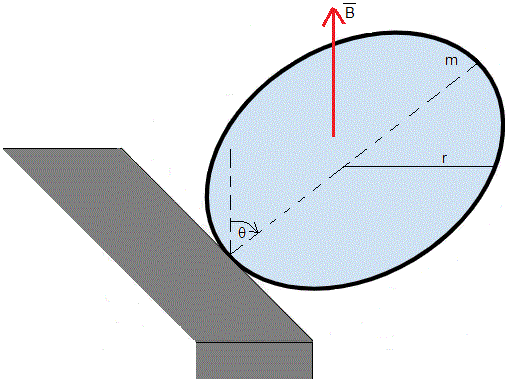
El enunciado del problema que vamos a resolver en esta página es el siguiente: Una moneda de cobre de r=10 cm de radio está situada sobre una mesa en posición casi vertical θ≈0. Se deja caer en el seno de un campo magnético uniforme B=2 T, cuya dirección es vertical. Calcular el tiempo T que tarda en llegar al suelo.

Sin campo magnético

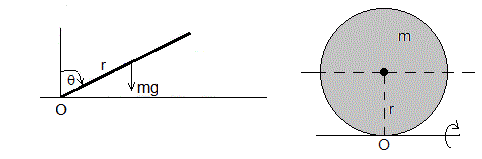
Cuando no hay campo magnético el problema es similar al estudiado en la página titulada Caída de una varilla inclinada, lo que cambia es el momento de inercia. El momento de inercia de un disco de masa m y radio r cuyo eje es paralelo al plano del disco y pasa por su centro, I_c=mr²/4. Aplicando el teorema de Steiner, si el eje es paralelo y pasa por el punto O de contacto en la mesa

${\displaystyle I=\frac{1}{4}m{r}^2+m{r}^2=\frac{5}{4}m{r}^2}$

La ecuación de la dinámica de rotación es

${\displaystyle \begin{array}{l}\frac{5}{4}m{r}^2\frac{d^2\theta }{d{t}^2}=mgr\sin \theta \\ \frac{d^2\theta }{d{t}^2}=\frac{4}{5}\frac{g}{r}\sin \theta \end{array}}$

mrgsinθ, es el momento del peso respecto del eje que pasa por O

Resolvemos esta ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, θ=θ₀, dθ/dt=0. El disco de radio r=10 cm, se desvía ligeramente de la posición vertical θ₀=0.1 rad (5.7°) y se suelta

function moneda_1
    r=0.01; %radio
    th_0=0.1; %ángulo inicial (5.7°)
    f=@(t,x) [x(2); 4*9.8*sin(x(1))/(5*r)]; 
    opts=odeset('events',@(t,x) stop_moneda(t,x));
    [t,x]=ode45(f,[0,10],[th_0,0],opts);

    subplot(2,1,1)
    plot(t, x(:,1))
    grid on
    xlabel('t')
    ylabel('\theta')
    title('Posición angular')

    subplot(2,1,2)
    plot(t, x(:,2))
    grid on
    xlabel('t')
    ylabel('d\theta/dt')
    title('Velocidad angular')

%tiempo, velocidad angular final
    disp('t,  w')
    disp([t(end),x(end,2)])
%Balance energético: energía potencial, energía cinética por unidad de masa
    Ep=9.8*r*cos(th_0);
    Ek=5*r^2*x(end,2)^2/8;
    disp('Ep,  Ek')
    disp([Ep,Ek])
%detiene el proceso de integración cuando el ángulo es 90°
    function [value,isterminal,direction]=stop_moneda(~,x)
        value=x(1)-pi/2; 
        isterminal=1;
        direction=1; 
    end
end

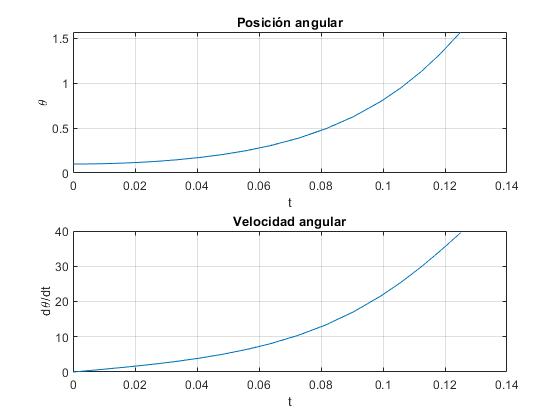
El tiempo que tarda en llegar al suelo es T=0.125 s y la velocidad angular final es 39.5 rad/s

t,  w
    0.1251   39.5177

La altura inicial del centro de masas es rcosθ₀. La energía potencial E_p=mgrcosθ₀ se convierte en energía cinética de rotación, E_k=Iω²/2. Las energías por unidad de masa E_p/m y E_k/m coinciden aproximadamente

Ep,  Ek
       0.0975    0.0976

Con campo magnético

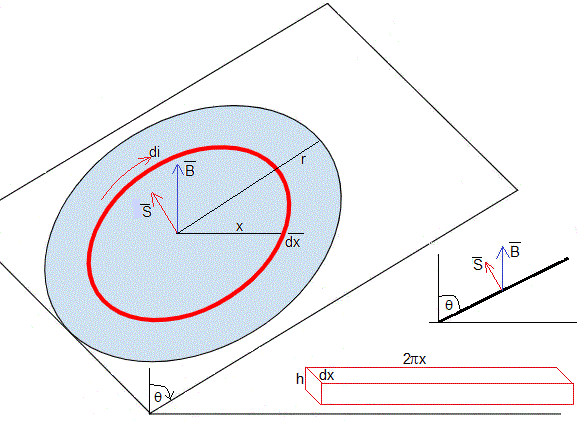
La figura muestra el disco en el instante t cuando forma un ángulo θ con la dirección vertical. Consideramos un anillo de radio x y anchura dx, en color rojo en la figura. El flujo del campo magnético a través de esta espira es

${\displaystyle \Phi =\overrightarrow{B}·\overrightarrow{S}=B\left(\pi x^2\right)\cos \left(\frac{\pi }{2}-\theta \right)=B\pi x^2\sin \theta }$

La fem inducida es

${\displaystyle V_{\epsilon }=-\frac{d\Phi }{dt}=-B\pi x^2\cos \theta \frac{d\theta }{dt}}$

El flujo va aumentando, el sentido de la corriente inducida es horario, la intensidad di que circula por la espira es el cociente entre la fem V_ε y la resistencia: 2πx es la longitud de la espira, h·dx es la sección de la espira y σ la conductividad del metal (cobre)

${\displaystyle di=\frac{B\pi x^2\cos \theta \frac{d\theta }{dt}}{\frac{1}{\sigma }\frac{2\pi x}{h·dx}}=\sigma \frac{xh}{2}B\cos \theta \frac{d\theta }{dt}dx}$

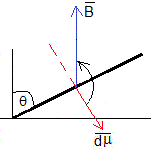
El campo magnético ejerce un momento sobre la corriente que circula por la espira. El momento magnético de la espira es dμ=di(πx²). El momento de la fuerza es el producto vectorial,

${\displaystyle \overrightarrow{dM}=\overrightarrow{d\mu }\times \overrightarrow{B}}$

El vector $\overrightarrow{d\mu }$, tiene la misma dirección y sentido contrario al vector $\overrightarrow{S}$. El módulo dM del momento de la fuerza que ejerce el campo magnético sobre la corriente inducida en la espira es

${\displaystyle dM=\left(di·\pi x^2\right)B·\sin \left(\frac{\pi }{2}-\theta \right)=\sigma \frac{\pi x^{3}h}{2}{B}^2{\cos }^2\theta \frac{d\theta }{dt}dx}$

Su dirección es el eje de rotación y su sentido es antihorario

Dinámica de rotación

El momento total M_B es

${\displaystyle M_B={\displaystyle \underset{0}{\overset{r}{\int }}\sigma \frac{\pi x^{3}h}{2}{B}^2{\cos }^2\theta \frac{d\theta }{dt}dx=\sigma \frac{\pi h}{2}{B}^2{\cos }^2\theta \frac{d\theta }{dt}}{\displaystyle \underset{0}{\overset{r}{\int }}{x}^3·dx}=\sigma \frac{\pi h{r}^4}{8}{B}^2{\cos }^2\theta \frac{d\theta }{dt}}$

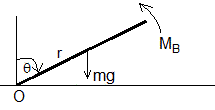
El momento del peso respecto del eje de rotación que pasa por O es mgrsinθ

La ecuación de la dinámica de rotación es

$I\frac{d^2\theta }{d{t}^2}=mgr\sin \theta -M_B$

Sustituyendo la masa m del disco por el producto, densidad ρ por volumen, πr²h

${\displaystyle \begin{array}{l}\frac{5}{4}\rho \pi r^{4}h\frac{d^2\theta }{d{t}^2}=\rho \pi r^{3}hg\sin \theta -\sigma \frac{\pi h{r}^4}{8}{B}^2{\cos }^2\theta \frac{d\theta }{dt}\\ \frac{d^2\theta }{d{t}^2}=\frac{4}{5}\frac{g}{r}\sin \theta -\frac{1}{10}\frac{\sigma }{\rho }{B}^2{\cos }^2\theta \frac{d\theta }{dt}\end{array}}$

Resolvemos esta ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, θ=θ₀, dθ/dt=0. El disco de radio r=10 cm, se desvía ligeramente de la posición vertical θ₀=0.1 rad (5.7°) y se suelta

La densidad del cobre es ρ=8.93·10³ kg/m³, la conductividad σ=5.714·10⁷ Ω^-1m^-1

function moneda
    rho=8930; %densidad
    sigma=5.714e7; %conductividad
    B=2; %campo magnético
    r=0.01; %radio
    th_0=0.1; %ángulo inicial

    f=@(t,x) [x(2); 4*9.8*sin(x(1))/(5*r)-sigma*B^2*cos(x(1))^2*x(2)/(10*rho)]; 
    opts=odeset('events',@(t,x) stop_moneda(t,x));
    [t,x]=ode45(f,[0,10],[th_0,0],opts);

    subplot(2,1,1)
    plot(t, x(:,1))
    grid on
    xlabel('t')
    ylabel('\theta')
    title('Posición angular')

    subplot(2,1,2)
    plot(t, x(:,2))
    grid on
    xlabel('t')
    ylabel('d\theta/dt')
    title('Velocidad angular')
    
%tiempo, velocidad angular final
    disp('t,  w')
    disp([t(end),x(end,2)])
%Balance energético: energía potencial, energía cinética, energía disipada
    Ep=9.8*r*cos(th_0);
    Ek=5*r^2*x(end,2)^2/8;
    ER=sigma*B^2*r^2*trapz(t,(cos(x(:,1)).*x(:,2)).^2)/(8*rho);
    disp('Ep,  Ek,    ER')
    disp([Ep,Ek,ER, Ek+ER])

    function [value,isterminal,direction]=stop_moneda(~,x)
        value=x(1)-pi/2; 
        isterminal=1;
        direction=1; 
    end
end

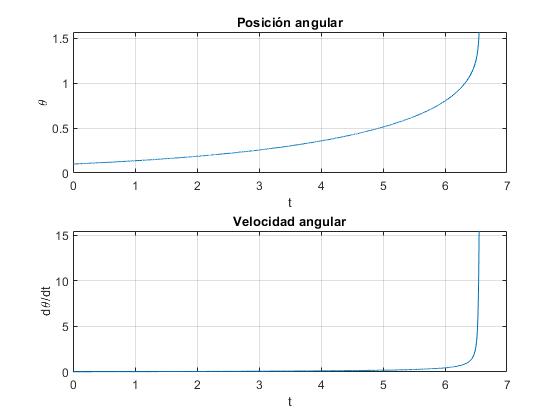
El tiempo que tarda es llegar al suelo es T=6.55 s (mucho mayor que la caída libre) y la velocidad angular final es 15.4 rad/s

t,  w
     6.5503   15.4472

Energías

La energía potencial E_p=mgrcos(θ₀) se convierte en parte, en energía cinética de rotación

${\displaystyle E_k=\frac{1}{2}\left(\frac{5}{4}m{r}^2\right){\left(\frac{d\theta }{dt}\right)}^2}$

La otra parte, se disipa en forma de calor

Para una espira de radio x, la energía por unidad de tiempo disipada es el cuadrado de la intensidad (di)² por la resistencia

${\displaystyle {\left(\sigma \frac{xh}{2}B\cos \theta \frac{d\theta }{dt}dx\right)}^2\frac{1}{\sigma }\frac{2\pi x}{h·dx}=\frac{1}{2}\pi \sigma h{B}^2{\cos }^2\theta {\left(\frac{d\theta }{dt}\right)}^2{x}^{3}dx}$

La energía por unidad de tiempo disipada por todas las espiras es

${\displaystyle {\displaystyle \underset{0}{\overset{r}{\int }}\frac{1}{2}\pi \sigma h{B}^2{\cos }^2\theta {\left(\frac{d\theta }{dt}\right)}^2{x}^{3}dx}=\frac{1}{2}\pi \sigma h{B}^2{\cos }^2\theta {\left(\frac{d\theta }{dt}\right)}^2{\displaystyle \underset{0}{\overset{r}{\int }}{x}^{3}dx}=\pi \sigma h{B}^2\frac{r^4}{8}{\cos }^2\theta {\left(\frac{d\theta }{dt}\right)}^2}$

La energía disipada en el tiempo T que dura la caída del disco es

${\displaystyle E_R={\displaystyle \underset{0}{\overset{T}{\int }}\frac{1}{8}\pi \sigma h{B}^2{r}^4{\cos }^2\theta {\left(\frac{d\theta }{dt}\right)}^{2}dt}=\frac{1}{8}\pi \sigma h{B}^2{r}^4{\displaystyle \underset{0}{\overset{T}{\int }}{\cos }^2\theta {\left(\frac{d\theta }{dt}\right)}^{2}dt}}$

Energía por unidad de masa disipada

${\displaystyle \frac{E_R}{m}=\frac{\frac{1}{8}\pi \sigma h{B}^2{r}^4{\displaystyle \underset{0}{\overset{T}{\int }}{\cos }^2\theta {\left(\frac{d\theta }{dt}\right)}^{2}dt}}{\rho \pi r^{2}h}=\frac{1}{8}\frac{\sigma }{\rho }{B}^2{r}^2{\displaystyle \underset{0}{\overset{T}{\int }}{\cos }^2\theta {\left(\frac{d\theta }{dt}\right)}^{2}dt}}$

Calculamos la integral mediante procedimientos numéricos utilizando la función trapz de MATLAB

Las energías por unidad de masa E_p/m, E_k/m y E_R/m son

Ep,  Ek, ER
      0.0975    0.0149    0.0826

Comprobamos que E_p/m=E_k/m+E_R/m, aproximadamente. Casi toda la energía potencial se disipa en forma de calor

Cálculo aproximado del tiempo de caída

Como observamos en la gráfica, durante la mayor parte del tiempo, la velocidad angular del disco crece muy lentamente, hasta el tiempo t≈6 s, la aceleración es casi nula. Igualamos el momento del peso mgrsinθ con el momento M_B que ejerce el campo magnético sobre las corrientes inducidas e integramos

${\displaystyle \begin{array}{l}\frac{4}{5}\frac{g}{r}\sin \theta =\frac{1}{10}\frac{\sigma }{\rho }{B}^2{\cos }^2\theta \frac{d\theta }{dt}\\ dt=\frac{1}{8}\frac{r}{g}\frac{\sigma }{\rho }{B}^2\frac{{\cos }^2\theta }{\sin \theta }d\theta \\ T=\frac{1}{8}\frac{r}{g}\frac{\sigma }{\rho }{B}^2{\displaystyle \underset{{\theta }_0}{\overset{\pi /2}{\int }}\frac{{\cos }^2\theta }{\sin \theta }d\theta }=\frac{1}{8}\frac{r}{g}\frac{\sigma }{\rho }{B}^2{\displaystyle \underset{{\theta }_0}{\overset{\pi /2}{\int }}\left(\frac{1}{\sin \theta }-\sin \theta \right)d\theta }\end{array}}$

El resultado de la primera integral es

${\displaystyle {\displaystyle \int \frac{dx}{\sin x}}=\frac{1}{2}{\displaystyle \int \frac{dx}{\sin \frac{x}{2}\cos \frac{x}{2}}}=\frac{1}{2}{\displaystyle \int \frac{dx}{\tan \frac{x}{2}{\cos }^2\frac{x}{2}}}={\displaystyle \int \frac{d(\tan \frac{x}{2})}{\tan \frac{x}{2}}}=\ln \left|\tan \frac{x}{2}\right|}$

El tiempo de caída T es

${\displaystyle T=\frac{1}{8}\frac{r}{g}\frac{\sigma }{\rho }{B}^2{\displaystyle \underset{{\theta }_0}{\overset{\pi /2}{\int }}\left(\frac{1}{\sin \theta }-\sin \theta \right)d\theta }=\frac{1}{8}\frac{r}{g}\frac{\sigma }{\rho }{B}^2\left(\ln \left(\tan \frac{\pi }{4}\right)-\ln \left(\tan \frac{{\theta }_0}{2}\right)-\cos {\theta }_0\right)}$

El tiempo que tarda en caer es T=6.53 s aproximadamente igual al obtenido mediante la ecuación diferencial

T=B^2*sigma*r*(log(tan(pi/4))-log(tan(th_0/2))-cos(th_0))/(8*9.8*rho)
T =   6.5289

Referencias

Lim Yung-kuo. Problems and Solutions on Electromagnetism. World Scientific (1993). Problem 2070, pp. 226-228

Datos de la densidad y conductividad del cobre

Koshkin N. I, Shirkévich M. G. Manual de física elemental. Edt. Mir, págs. 36 y 139