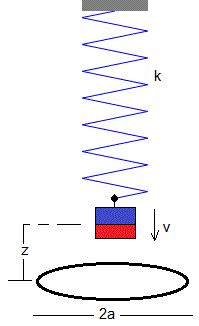
Sea un muelle de constante k suspendido verticalmente. Se cuelga de su extremo libre inferior un potente imán de momento magnético μ. A una distancia z=z₀ por debajo del imán se coloca una bobina formada por un conjunto de N espiras apretadas del mismo radio a.

Al moverse el imán, el campo magnético variable induce una corriente en las espiras de la bobina. Dicha corriente establece una fuerza sobre el imán que se opone a su velocidad. Observaremos oscilaciones cuya amplitud va decreciendo con el tiempo.

Flujo a través de una espira y f.e.m.

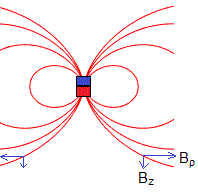
En la página, Campo magnético producido por una imán hemos supuesto que un imán se comporta como un dipolo magnético de momento μ. Las componentes del campo son

${\displaystyle \begin{array}{l}{B}_{\rho }=\frac{{\mu }_0\mu }{4\pi }\frac{3\rho z}{{\left({\rho }^2+z^2\right)}^{5/2}}\hfill \\ B_z=\frac{{\mu }_0\mu }{4\pi }\frac{2z^2-{\rho }^2}{{\left({\rho }^2+z^2\right)}^{5/2}}=\frac{{\mu }_0\mu }{4\pi }\left\{\frac{3z^2}{{\left({\rho }^2+z^2\right)}^{5/2}}-\frac{1}{{\left({\rho }^2+z^2\right)}^{3/2}}\right\}\hfill \end{array}}$

El flujo del campo producido por el imán a través de una bobina formada por N espiras apretadas del mismo radio a, es.

${\displaystyle \Phi =N\underset{S}{{\displaystyle \int }}\overrightarrow{B}\cdot \overrightarrow{dS}=N\underset{S}{{\displaystyle \int }}(B_{\rho }\widehat{j}+B_z\widehat{k})\cdot dS·\widehat{k}=-N\underset{S}{{\displaystyle \int }}{B}_z·dS}$

El flujo depende solamente de la componente B_z del campo magnético

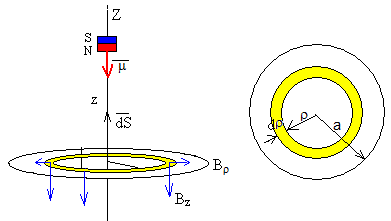
El elemento diferencial de superficie dS, es el área de un anillo de radio ρ y de espesor dρ, su valor es dS=2πρ·dρ

${\displaystyle \begin{array}{l}\Phi =-{\displaystyle N\underset{0}{\overset{a}{\int }}\frac{{\mu }_0·\mu }{4\pi }\left(\frac{3z^2}{{\left(\sqrt{{\rho }^2+z^2}\right)}^5}-\frac{1}{{\left(\sqrt{{\rho }^2+z^2}\right)}^3}\right)2\pi \rho ·d\rho }\\ \Phi =-\frac{N{\mu }_0·\mu }{4}\left(3z^2{\displaystyle \underset{0}{\overset{a}{\int }}\frac{2\rho ·d\rho }{{\left(\sqrt{{\rho }^2+z^2}\right)}^5}-}{\displaystyle \underset{0}{\overset{b}{\int }}\frac{2\rho ·d\rho }{{\left(\sqrt{{\rho }^2+z^2}\right)}^3}}\right)=-\frac{N{\mu }_0\mu ·a^2}{2{\left(\sqrt{a^2+z^2}\right)}^3}\end{array}}$

Aplicando la ley de Faraday

${\displaystyle V_{\epsilon }=-\frac{d\Phi }{dt}=-\frac{d\Phi }{dz}\frac{dz}{dt}=-\frac{d\Phi }{dz}(-v)=\frac{3N{\mu }_0\mu a^2}{2}\frac{zv}{{\left(a^2+z^2\right)}^{5/2}}}$

Supongamos una espira de radio a y de sección circular cuyo diámetro es D, está hecha de un material cuya conductividad es σ. La resistencia de la espira es

${\displaystyle R=\frac{1}{\sigma }\frac{2\pi a}{\frac{\pi }{4}{D}^2}}$

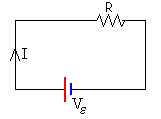
La resistencia de la bobina es NR. La ley de Ohm para este anillo se escribe V_ε=i·NR. La intensidad i de la corriente inducida en la espira es

${\displaystyle i=\frac{3{\mu }_0\mu \sigma D^2}{16}\frac{az}{{\left(\sqrt{a^2+z^2}\right)}^5}v}$

La fuerza que ejerce el campo magnético producido por el imán sobre la corriente inducida i en la bobina es

${\displaystyle \overrightarrow{F}=i({\widehat{u}}_t\times \overrightarrow{B})N(2\pi a)}$

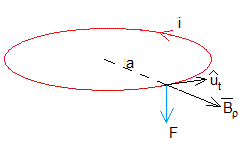
La componente B_ρ del campo magnético ejerce una fuerza a lo largo del eje Z y la componente B_z ejerce una fuerza a lo largo de la dirección radial que no tiene efecto alguno sobre la bobina. El módulo de la fuerza a lo largo del eje Z es

${\displaystyle \begin{array}{l}F=iN\left(2\pi a\right)B_{\rho }=\left(\frac{3{\mu }_0\mu \sigma D^2}{16}\frac{az}{{\left(\sqrt{a^2+z^2}\right)}^5}v\right)N\left(2\pi a\right)\left(\frac{{\mu }_0\mu }{4\pi }\frac{3az}{{\left(\sqrt{z^2+a^2}\right)}^5}\right)=\\ \frac{9{\mu }_0^2{\mu }^2\sigma D^{2}N}{32}\frac{a^3{z}^2}{{\left(a^2+z^2\right)}^5}v\end{array}}$

Aplicando la tercera ley de Newton, esta es la fuerza que la corriente inducida ejerce sobre el imán.

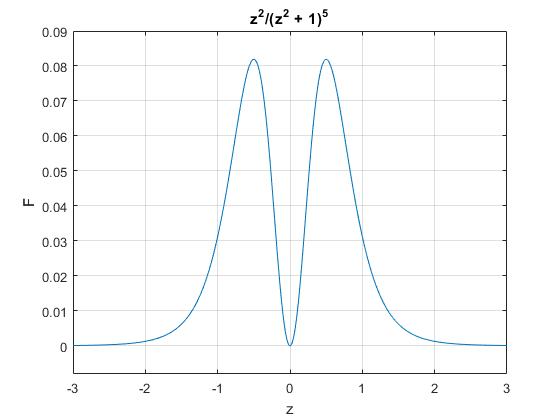
La fuerza es proporcional a

${\displaystyle y=\frac{z^2}{{\left(a^2+z^2\right)}^5}}$

La fuerza es máxima cuando z=±a/2, tal como comprobamos con el código MATLAB

>> syms a z;
>> y=z^2/(a^2+z^2)^5;
>> yy=diff(y,z);
>> solve(yy)
ans =
    0
  a/2
 -a/2
>> y=subs(y,a,1);
>> ezplot(y,[-3,3])
>> grid on
>> xlabel('z')
>> ylabel('F')

Ecuación del movimiento

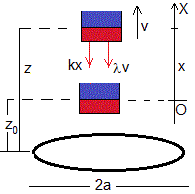
La fuerza que se opone al movimiento del imán es proporcional a la velocidad v y de sentido contrario.

Sea z₀ la altura inicial del imán sobre la bobina. Cuando el imán se desplaza x=z-z₀ de la posición de equilibrio las fuerzas que actúan sobre el imán son:

• La fuerza que ejerce el muelle deformado kx, siendo k es la constante del muelle
• La fuerza λv que ejercen la corriente inducida en la bobina sobre el imán, donde λ es una función de z o de x=z-z₀

La ecuación del movimiento del imán es

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=-\lambda \frac{dx}{dt}-kx\\ \frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}+{\omega }_0^{2}x=0\end{array}}$

Integramos la ecuación diferencial con las condiciones iniciales siguientes: en el instante t=0, la posición del imán es x₀ y su velocidad es v=0.

Oscilaciones amortiguadas

En una primera aproximación, vamos a suponer que la fuerza F=λv que ejercen las corrientes inducidas sobre el imán, no cambia con la altura z del imán, de modo que λ es constante e igual a

${\displaystyle \lambda =\frac{9{\mu }_0^2{\mu }^{2}N\sigma D^2}{32}\frac{a^3{z}_0^2}{{\left(a^2+z_0^2\right)}^5}}$

Siendo z₀, la separación inicial. La solución de la ecuación diferencial con las condiciones iniciales: en el instante t=0, la posición inicial es x=x₀ y la velocidad inicial es v₀ es (véase Oscilaciones amortiguadas)

${\displaystyle \begin{array}{l}\omega =\sqrt{{\omega }_0^2-{\gamma }^2}\\ x=\exp (-\gamma t)\left(\frac{v_0+\gamma x_0}{\omega }\sin (\omega t)+x_0\cos (\omega t)\right)\end{array}}$

Caso general

En el caso general, λ y por tanto, γ es una función de la separación z entre el imán y la placa metálica.

${\displaystyle \lambda =\frac{9{\mu }_0^2{\mu }^{2}N\sigma D^2}{32}\frac{a^3{z}^2}{{\left(a^2+z^2\right)}^5}}$

Resolvemos la ecuación diferencial por procedimientos numéricos con las condiciones iniciales: en el instante t=0, la posición inicial es x=x₀ y la velocidad inicial es v₀. Representamos la posición x del imán en función del tiempo t, en color rojo la aproximación con λ constante, en color azul la solución numérica con γ función de la separación z. Se han tomado del artículo mencionado en las referencias, los siguientes valores de los parámetros:

• Constante elástica del muelle, k=3.17 N/m
• Masa del imán, m= 55 g
• Momento magnético del imán, μ=2.6 Am²
• Número de epsiras que froman la bobina, N=10
• Radio de las espiras, a=15 mm
• Conductividad del material del que está hecho el cable, σ=2.741·10⁷ Ω^-1m^-1
• Diámetro de la sección del cable, D=1.5 mm
• Separación inicial entre el imán en equilibrio y la bobina, z₀=17 mm
• El imán se separa x₀=10 mm de la posición de equilibrio y se suelta
• Velocidad inicial del imán, v₀=0, parte del reposo

m=55/1000; %masa del imán
k=3.17; %constante elástica
mu=2.6; %Am2, momento magnético
sigma=2.741e7; %conductividad
D=1.5/10; %diámetro de la sección del cable
z0=17/10; %separación inicial en cm
a=15/10; %radio de la espira en cm
N=10; %número de espiras
w0=sqrt(k/m); %frecuencia angular propia
gg=N*9*(4*pi*1e-7)^2*mu^2*sigma*D^2*a^3*1e6/(32*2*m); %rozamiento, gamma,
g=gg*z0^2/(a^2+z0^2)^5;
w=sqrt(w0^2-g^2);
x0=[10/10,0];  %condiciones iniciales: [posición inical en cm, velocidad inicial]
tspan=[0 10*2*pi/w0;];  %diez periodos

%oscilaciones amortiguadas
xx=@(t) exp(-g*t)*((x0(2)+g*x0(1))*sin(w*t)/w+x0(1)*cos(w*t));
%solución numérica
f=@(t,x) [x(2);-2*gg*x(2)*(x(1)+z0)^2/((x(1)+z0)^2+a^2)^5-w0*w0*x(1)]; 
[t,x]=ode45(f,tspan,x0);

hold on
plot(t,x(:,1), 'b')
fplot(xx,tspan, 'r')
hold off
legend('solución numérica','oscilación amortiguada')
xlabel('t(s)')
ylabel('x(cm)');
title('Oscilador amortiguado')
grid on

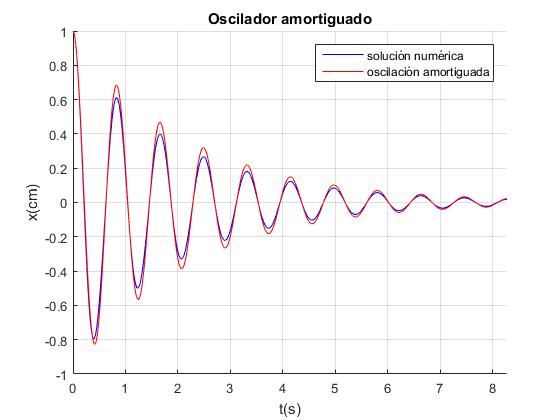
Cuando desplazamos el imán x₀=10 mm de la posición de equilibrio y lo soltamos, apreciamos una pequeña diferencia entre la solución numérica y la aproximación de las oscilaciones amortiguadas.

Actividades

Se introduce

• El desplazamiento inicial del imán x₀ en mm, en el control titulado Desplazamiento inicial del imán
• La separación inicial entre el imán y la bobina z₀ en mm, en el control titulado Separación inicial imán-bobina.
• El número de espiras N de la bobina, en el control tituado Número de espiras

El programa ha fijado los siguientes parámetros:

• Masa del imán, m=55 g
• Momento magnético del imán, μ=2.6 Am²
• Radio de las espiras, a=15 mm
• Conductividad del material del que están hechas las espiras, σ=2.741·10⁷ Ω^-1m^-1
• Diámetro de la sección del cable, D=1.5 mm
• Constante elástica del muelle, k=3.17 N/m
• Velocidad inicial del imán, v₀=0, parte del reposo

Se pulsa el botón titulado Nuevo.

Una circunferencia de radio a representa las espiras de la bobina, los puntos de color rojo representan los portadores de carga positiva, su movimiento nos da una idea del sentido de las corrientes inducidas en las espiras cuando se mueve el imán

La flecha situada a la izquierda del imán, representa la fuerza que ejercen las corrientes inducidas sobre el imán, se trata de una fuerza proporcional a la velocidad y de sentido contrario a la misma.